等价转化思想在高中数学解题中的应用

杨新运

（厦门市新店中学，福建 厦门 361102）

等价转化思想在高中数学解题中的应用

杨新运

（厦门市新店中学，福建 厦门 361102）

在高中数学解题过程中，等价转化能为许多问题的求解指明方向：将陌生问题熟悉化，将复杂问题简单化，将抽象问题具体化，将直接问题间接化等。

高中数学；等价转化思想；问题解决

等价转化思想指的是在研究和解决有关数学问题时，通过某种手段或技巧，把问题转变到一类已经解决、或者比较容易解决的问题，进而解决问题的一种思路和方法。《普通高中数学课程标准（2003实验版）》指出“高中数学课程应重视提高学生的数学思维能力”，而等价转化的思想其实就是一种重要的数学思维能力。在等价转化过程中，一般是化繁为简，化难为易，即对原来问题中的条件进行整理、变形、转换，最后将原问题化归为简单的和熟悉的问题。教师在数学解题教学过程中，应注重引导学生运用等价转化思想解决问题。

一、将陌生问题熟悉化

在高中数学解题过程中，常常把陌生的问题转化成熟悉的问题，再用既定的方法解决问题，数列递推求通项问题的求解就是这种等价转化思想的体现。

分析：本题如果赋值求解，困难较大，但是若把数列{an}的递推公式进行整理变形便能转化成学生熟悉的等差数列，就容易求出通项公式。

本题主要把求数列{an}的通项公式通过变形转化为求数列的通项公式，即变成求学生熟悉的等差数列的通项公式。因此，有些数列虽然不是等差或等比数列，但学生可以通过变形、化简，转化为熟悉的特殊的数列来解决。这种把陌生的问题转化成熟悉的问题的转化方法在数学解题中应用非常广泛。

例2.设函数 f(x)在 R上的导函数是 f′(x)，对 ∀x∈R ，f′(x)＜x ，若 f(1-a)-f(a)≤-a，求实数a的取值范围。

分析：这道题的题干很简单，但是不易找到解题思路，经过认真的分析后，可将已知条件进行等价转化：

进而

这道题把本来看似陌生、不易解决的问题，通过等价转化变成熟悉的函数的单调性问题来解决，转化之后的构造函数是解题的重点，而最初的等价转化才是解决问题的关键。

二、将复杂问题简单化

对于一些数学问题，从正面直接解答或用特定方法解答比较复杂，若能转换解答思路或变换考虑问题的角度，往往可以把复杂的问题变得简单，解决起来也比较快捷。

例 3.已 知 a+b+c=1,a＞0,b＞0,c＞0 ，求 证 ：

证明不等式时，常利用已知条件通过适当变换，将未知的条件等价转化为常见的已有的条件，用既定的方法去解决实际问题。要注意找到问题中的已知条件和结论之间的联系，挖掘出隐含条件，把复杂的问题转化成相对简单、容易突破的问题。

分析：通常的解法是将cos2x=1－sin2x代入已知的式子，然后令t=sin2x，换元进行整理变化，然后求最值。如果改变一下思路，进行一下等价转化，问题就会变得更简单：

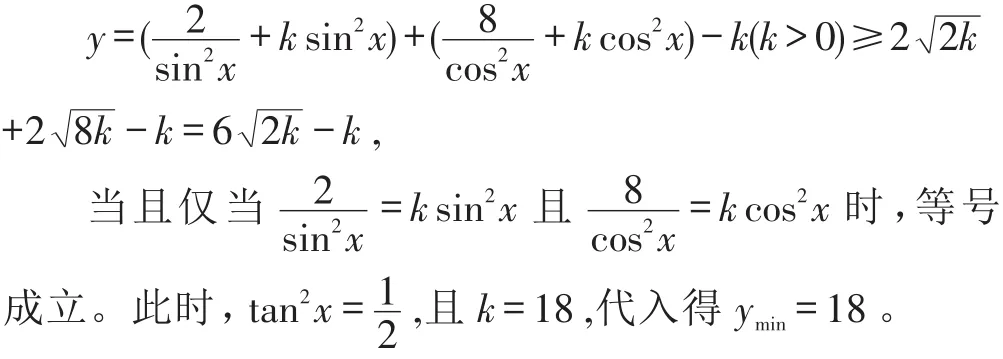
本题不用三角换元，去分母，进行繁琐的化简，而是对原函数进行等价转化，从而运用基本不等式求最值，把复杂的解题思路变得简单，这里等价变形起到了关键的作用。由此可见，对一些复杂的数学问题，经过一定的等价转化，可以达到简化计算的目的。解题时，应该让学生明白，碰到复杂问题时，先进行等价转化，把复杂问题变得相对简单后，再进行求解计算。

三、将抽象问题具体化

在数学解题过程中，经常还会碰到一些抽象的数学问题，这些问题往往给出的条件非常少，不易直接求解或推导，需要进行一系列的等价转化，才能变成具体的、容易求解的数学问题。

例5.设定义在 R上的函数 f(x)满足f(x)·f(x+2)=13，若 f(1)=2 ，求 f(99)的值。

分析：这是一个抽象函数问题，没有给出函数的一些性质，直接求解几乎是不可能的事情。所以要对已知条件进行等价转化：

把抽象问题具体化是在数学解题中常用的转化手段，在抽象问题与具体函数间建立联系，从而把抽象问题具体化。

例6.在直径为d的圆木中，截取一个具有最大抗弯强度的长方体梁，则矩形面的长为________(强度与 bh2成正比，其中h为矩形的长，b为矩形的宽)。

分析：本题是一个小的应用题，条件少，抽象性强，不易找到解题突破口。认真思考后，可画出截面图如下，把抽象的问题转化成具体图形问题，再进行化简求值。

如图为圆木的横截面，∵b2+h2=d2∴bh2=b(d2-b2)

以上两个问题主要是把抽象问题或应用问题等价转化为具体的数学问题，然后利用函数的周期性，或借助几何图形，再结合学过的函数知识加以解决。题目难度虽然不是很大，但是如果不进行等价转化，便不好找解题思路，甚至无从下手。因此，等价转化的步骤是解决问题的重要前提，应引导学生在解题中认真领悟、用心总结，掌握常用的等价转化技巧，从而提高解决数学问题能力。

四、将直接问题间接化

有一些数学问题，直接求解时，分类情况较多，解答起来相对复杂，且易遗漏或重复。当正面分类情况较多时，反面的情况相对就较少，因此用间接方法解答，问题就会更简单。

例7.一条长椅上有7个座位，4个人坐，还有3个空位子，求：(1)至少有两人坐在一起，有多少种不同的坐法？(2)三个空位不都相邻，有多少种不同的坐法？

例8.某班甲、乙、丙三名同学参加省数学竞赛选拔考试，成绩合格可获得参加竞赛的资格。其中甲同学表示成绩合格就去参加，但乙、丙同学约定：两人成绩都合格才一同参加，否则都不参加。设每人成绩合格的概率为ffffdd，求三人至少有一人成绩合格的概率。

分析：这个问题中又是含有“至少”的字眼，总共有三人，正面求解分类较多，比较复杂，所以考虑用间接方法处理问题。

略解：用事件A、B、C分别表示为“甲、乙、丙三人成绩合格”，由题意知A、B、C三个事件相互独立，且那么成绩合格的概率为

因此，对于一些数学问题，如果从条件出发，正面分析问题时，分类情况较多，解答过程比较繁琐，可以考虑分析问题的条件或结论的反面情况。也就是把直接问题间接化，可以减少分类讨论，简化解题过程，使问题得以较快地解决。

五、结语

等价转化的思想方法在高中数学解题过程中起着举足轻重的作用,教师应引导学生重视等价转化的思想方法在解题中的运用。但由于等价转化思想具有一定的灵活性，解题时要先设计好等价转化的方法和思路，避免生搬硬套，造成解题失误。要引导学生把数学问题，从高次往低次转化，变成比较简单的问题；或者由抽象往具体转化，变成比较直观的问题；或者从非标准型往标准型转化，变成我们的熟悉的公式或结论；或者将非线性的问题往线性问题转化，变成常规的代数运算等等。按照这些原则进行解题操作，可畅通无阻地攻克许多高中数学难题。教师在解题教学时，应经常渗透等价转化的思想方法，这样即可以提升学生的数学解题能力又可以培养学生良好的数学思维品质。

［1］教育部.普通高中数学课程标准（实验）［M］.北京：人民教育出版社，2003.

［2］方亚斌.怎样认识新课标中的基本不等式［J］.数学通报，2013（2）．

［3］张中发.例谈等价转化思想在解高考题中的应用［J］.中学数学研究，2011（3）.

［4］齐如意.函数问题中的等价转化思想［J］.中学数学研究，2004（6）.

［5］吴桂芬.如何提高“解题教学”课的教学效率［J］.新课程研究（基础教育），2010（1）.

（责任编辑：王钦敏）