探讨混沌分析在中长期水文预测中的应用和展望

文/马志贵,国电新疆吉林台水电开发有限公司

探讨混沌分析在中长期水文预测中的应用和展望

文/马志贵,国电新疆吉林台水电开发有限公司

本文首先介绍了基于混沌理论的中长期水文预测识别方法，然后探讨了基于混沌分析法在中长期水文预测中的具体应用，最后分析了基于混沌分析法在水文系统的中长期预测。

混沌分析法；中长期水文预测；识别方法；应用

要将混沌理论应用于水文预测中，首先就需判别水文系统的运动形式是否为混沌运动，即进行混沌性识别或序列性质鉴别，然后才可借助于水文序列的相空间，并应用混沌分析方法，在水文序列的相空间中分析水文系统的运动规律，最后再在上述分析基础上，作进一步的诸如混沌预测方法等研究。所以重建水文系统相空间，水文序列性质鉴别(即水文系统混沌性识别)及水文混沌预测方法是混沌分析法在水文预测中所面临的三大关键问题。

1 基于混沌理论的中长期水文预测识别方法

1.1 饱和分维数

维数作为空间以及客体的重要几何参量，空间运动过程中其所需要变量个数．利用状态空间中的维数进行反映，并且，吸引子所表示的是其所必需的信息量。一般来讲，将吸引子定义为经过长时间的演化之后。其所能形成的最终状态。水文动力系统中．吸引子可以将其概括为三类：平衡点、极限环以及混沌吸引子对于混沌吸引子而言．其作为一种分形结构，本身并不具有特征尺度，因此可以将混沌吸引子定义为分数维．可以用下式进行表达：

在上式中，将e表示为V维空间中的子集，M(X)为覆盖e所需的边长为X的V维立方体的最小数目。并且．如果在重构的相空间中可以得到相对小的分维数，就可以认定此水文

系统具有混定性特征。饱和分维数的分析方法是目前较为常用的识别混沌特性的分析方法．得到很大程度上的应用。

1.2 Lyapunov指数

Lyapunov指数被应用于量化初始相近的轨道指数所发散出以及估计系统的混沌量，并且能够从整体上对水文系统的混沌量水平进行反映．从而凸显出系统的混沌性特征。最小李

雅普诺夫指数对轨道收缩快慢起到决定性作用．最大李雅普诺夫指数则是对轨道发散覆盖整个吸引子的快慢以及可预报时间的尺度。同时，所有的李雅普诺夫指数从整体上的表现出了轨道总的发散快慢。例如，如下式中所提到的一维映射：

Xn+1=f(Xn)

一维映射状态下．只有一个拉伸以及折叠的方向，因此可以对初值x0以及近邻值x0+Wx0，进而，由下式即可以做出一次迭代进行两点之间的距离计算：

在经过N次迭代后．两点之间的距离即可以将其用下式表示：

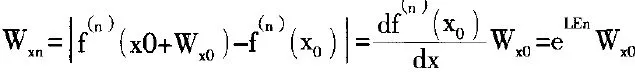
进而推导出李雅普诺夫特征指数：

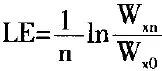
一维映射的运算过程中．只有唯一的李雅普诺夫指数，并且其面，临着三种状况．分别是大于、小于以及等于零。最大的李雅普诺夫指数为正．就可以作为动力系统是否为混沌性质的重要条件，其倒数也可以将其作为最大可预测长度的估计值。

1.3 K熵

Kolmogorov熵可以简称K熵，其是指系统在一定时间内，其所产生的平均信息量的一种上限。被用来表示度量系统运动的混乱以及无序所产生的程度值。测度熵是一种精确化的

信息熵，用来表示信息损失率的平均值．也能够区别规则运动、混沌运动以及随机运动。测度熵所代表的是 Lyapunov指数之和，用来体现系统的无序程度。将其分为三种情况：K=0即表示系统正处于规则运动状态，K=+∞时，系统处于随机运动状态，0＜K＜+∞时，系统处于混沌运动，以此来作为判断混沌运动的标准

2 基于混沌分析法在中长期水文预测中的具体应用

对所具有的混沌特征的水文系统，其本身所具有的吸引子对初始条件有敏感与依赖性．在一定时间段内轨道发散较小，信息损失程度也相对较少。对中长期水文预测具备一定的基础条件传统的水文动力系统预测模式以及统计预测模式与相空间之间进行紧密联系，从而使水文预测方法更加具有系统性。最近一些年来，混沌分析法的研究成果主要集中在了水文时间的序列的预测部分。传统的动力学方法以及数理统计方法需要首先建立数据序列的主观模型，并依据此类进行预测与计算。利用混沌分析方法，可以在不建立主观模型的情况下对数据序列直接计算．从而以此分析出客观规律，并进行预测。此举的优势在于避免了人为主观性对预测过程的干扰，从而进一步提升了预测的精度以及可信度在实际的混沌预测过程中，需要事先利用假想未知相点以及已知相点．从而以此作为线性或非线性的函数关系的基本条件。其次，根据数据资料利用数理统计理论以及方法．建立相点模为变量以及应变量的预报方程。或者是根据数据资料．从众多的可能性多项式关系中．对理想函数关系进行自动选择，从而获得预报方程。利用已知系统的动力模式，将会在混沌预测中获得极大的积极意义。

3 基于混沌分析法在水文系统的中长期预测分析

我国河流众多，水域复杂，建立统一、系统性的数学模型缺乏理论与实践上的基本条件。通过寻求新的方法．例如复杂性科学、分形理论等多种手段对观测数据进行分析．尤其是以

混沌分析法作为主要的分析方法河道水位流量中长期预报本身难度较大。其形成受多种因素相互作用而形成。利用混沌分析法，能够在一定程度上避免人为主观能动性，降低了建立数学模型的难度．从而为模拟水流动力学特征提供了重要的数据支持．对于河道水位流量预报的精准度以及可靠性有着很大的提升作用。在混沌分析法在河道水位流量预报中需要着重解决几项问题：①河道水位流量要素所具有的混沌特征识别、演化成因机理以及形成条件；②分析时间序列过程中，需要具备无限长以及无噪音的特点；③定量描述水流要素混沌演化规律以及其在时空尺度上的变化；④定量描述水流要素混沌演化成因机理以及演化规律间的因果关系。

4 结语

水文系统在运行过程中。受到各种客观条件的影响，其时空变异性较强．所展现出的随机性与貌似随机性特点给水文预测带来了相当大的困难。混沌分析法的应用，在很大程度高

上解决了传统预测方式的弊端，两者之间的有效结合．很大程度上提升了水文预测的精度与可靠性。但是，在复杂水文状况中，如何利用混沌分析方法提升中长期预报的准确性．需要进一步加以分析与研究

[1]雷苗.面向混沌时间序列预测的隐式特征提取算法[J].仪器仪表学报，2014，35(1)

[2]张坤.红河流域月径流时间序列的混沌特性分析[J].人民珠江，2013，34(4)

[3]丁红.小波分析在径流时间序列预测的应用[J].柳州师专学报，2012．27(3)