敏捷卫星立体成像覆盖能力分析

王中果 李贞 汤海涛 鲁帆 田志新 李劲东

(北京空间飞行器总体设计部，北京 100094)

敏捷卫星立体成像覆盖能力分析

王中果 李贞 汤海涛 鲁帆 田志新 李劲东

(北京空间飞行器总体设计部，北京 100094)

成像幅宽确定时，敏捷卫星的覆盖能力仅取决于成像条带长度。根据敏捷卫星的立体成像过程，推导出基于圆形地球模型星下点轨迹下的立体成像条带长度通用公式，分析了敏捷卫星实现立体成像的最小机动能力需求，并推导出立体成像条带长度所对应的姿态机动能力需求通用公式。基于某卫星典型姿态机动能力进行实际应用分析，得到轨道高度、俯仰预置角、立体观测视角数量等因素对其影响规律。分析结果表明：在其他条件相同时，轨道高度增加或俯仰预置角增大，均会带来立体成像条带长度增加，双视立体成像获取的条带长度也大于三视立体成像。文章采用的分析方法和推导出的相关公式，可为敏捷卫星的总体分析设计提供参考。

敏捷卫星；立体成像；覆盖能力；条带长度；姿态机动能力

1 引言

敏捷卫星是指能够在短时间内实现大角度快速机动的卫星，可沿三轴进行转动，利用其快速姿态机动能力，迅速改变星上相机对地指向，实现对地面目标高效、灵活的观测[1]。基于其优异的姿态机动能力，敏捷卫星可以实现多种新型的成像模式，如同轨多点目标成像、同轨立体成像、同轨多条带拼幅成像等[2]。其中，同轨立体成像模式是指对同一地区实现不同角度的观测以形成立体像对，从而得出该地区的三维成像信息[3]，该模式主要利用卫星俯仰轴的快速姿态机动来实现同轨2次或2次以上对同一地面目标不同角度的观测。与传统对地观测卫星(如陆地资源卫星、海洋卫星、测绘卫星)的大面积、长条带成像方式不同，敏捷卫星重点完成对感兴趣点目标(或小区域目标)的小面积、短条带、及时、多角度详细成像观测。

一般情况下，专用立体成像测绘卫星采用双线阵或三线阵测绘体制，安装不同指向的2台或3台相机来完成立体观测任务，其最大的优势是可长时间开机进行连续长条带成像。双线阵测绘卫星通常采用前视相机、后视相机的视线指向与星下点夹角相同的工作方式，在轨从前、后2个方向获取同一地面目标分辨率相同的双视立体影像。与双线阵测绘卫星相比，三线阵测绘卫星增加了1台指向星下点的正视相机，在轨从前、正、后3个方向获取同一地面目标的“三视立体影像”。但随着空间分辨率的进一步提高，相机尺寸急剧增大，卫星平台难以同时承载2台或3台大尺寸相机。而敏捷卫星利用俯仰轴快速姿态机动，可在短时间内实现对同一地面目标的不同角度观测(对应于三线阵或双线阵测绘卫星上不同相机观测视角)，并形成立体像对，以满足立体观测需求[4]。因此，敏捷卫星的同轨立体成像模式不仅解决了安装多台相机导致遥感卫星承载能力过大的问题，并且降低了卫星的经济成本和研制难度[5]。

目前，国内外对敏捷卫星的研究已取得了不少成果，但主要集中在姿态机动稳定控制[6-9]、同轨多点目标任务规划[10-11]、同轨多条带拼幅成像[1，12-13]等方面，而对同轨立体成像相关研究却很少。文献[2]中对同轨立体成像时不同重叠条带长度对所需姿态机动能力进行了分析，但采用了平面地球模型，未考虑地球曲率的影响，与实际情况有所偏差。文献[4]中针对敏捷卫星的同轨立体成像模式，从立体像对成像质量的角度出发，提出了一种基于步进搜索策略的成像规划方法，但其计算模型较为复杂、不直观。此外，敏捷卫星立体成像覆盖能力的简化分析方法，也尚未见到相关报道。

本文针对敏捷卫星特定立体成像覆盖能力对轨道高度、姿态机动能力等指标的工程应用需求，采用圆形地球模型推导出敏捷卫星双视、三视立体成像条带长度的通用公式，以及立体成像的姿态机动能力需求通用公式，并结合卫星典型姿态机动能力，分析了不同轨道高度、不同俯仰观测角度、不同视角数量的成像条带长度变化规律，可为后续敏捷卫星工程应用提供参考。

2 立体成像覆盖能力分析

2.1立体成像过程分析

由于成像覆盖能力为卫星幅宽与条带长度的乘积，在卫星幅宽确定的情况下，条带长度决定了成像覆盖能力，因此仅分析条带长度即可。为简化分析过程，暂不考虑地球椭率和自转的影响，也不考虑滚动方向的姿态机动(实际应用时，立体成像的主要用途是立体测绘，滚动方向的侧摆角可以为较小的非零值，但要保证此侧摆角、俯仰角组合下的目标定位精度满足需求)。双线阵测绘和三线阵测绘的基本原理相同，都是利用不同基线位置测量的图像，通过像对匹配，采用摄影测量原理，计算出目标到摄影时刻卫星所处位置之间的相对距离，结合高精度的轨道测量数据和高精度的时间数据，计算出目标地形的高度。三线阵成像与双线阵成像之间的最大区别，是推扫区域内任意一个地面点均有3个不同角度观测到的影像(即前视、正视和后视影像)，3个线阵CCD推扫条带影像相互重叠，较双线阵成像增加了正视影像。采用三线阵测绘方式实现测图功能，可以按照三线阵CCD影像空中三角测量光束法平差的方法，以三线阵CCD影像本身计算外方位元素，从而大大降低对卫星姿态稳定度的要求[14]。与之对应，采用敏捷卫星单线阵CCD相机立体成像时，可沿轨道方向前后摆动，以一定交会角进行双视立体成像或者三视立体成像，并经摄影测量处理对目标进行高程定位。

1)双视立体成像

在圆形地球模型下，双视立体成像过程示意如图1所示，2个视角观测区域的重叠部分为立体成像区域。图1中：地球半径Re为固定值，取为6371 km；H为轨道高度(km)；Vs为卫星飞行速度(km/s);ωe为轨道角速度。考虑卫星侧摆角为0°，通过调整俯仰角实现立体观测，可分为3个步骤。

(1)卫星“抬头看”，正方向俯仰至θ1(即条带1预置角度)，成像时长为t1，对应轨迹为条带1，其中θ1>0。

(2)卫星反方向俯仰机动，经过时长t3回头至俯仰角-θ2(即条带2预置角度)，其中θ2≥0。

(3)保持俯仰角-θ2“回头看”，成像时长t2,对应轨迹为条带2。

为确保条带2的起始点位于条带1上面(图1中蓝色的条带2比红色的条带1更短一些)，t1需要足够大，而t2选择为合适参数时，可确保条带2的终点与条带1的终点重合。

2)三视立体成像

敏捷卫星获取三视立体图像时，需要在双视立体成像3个步骤后再增加2个步骤。考虑到第1次和第3次预置俯仰角大小相同、正负号相反，前视至正视、正视至后视的机动过程用时相同，正视、后视保持时间也相同，三视立体成像过程可重新定义如下。

(1)卫星“抬头看”，正方向俯仰至θ，成像时长为t1，对应轨迹条带1，其中θ>0。

(2)卫星反方向俯仰机动，经过时长t3回头至俯仰角0°(相当于双视立体成像中的第2个观测俯仰角为0°)。

(3)保持俯仰角0°“正视看”，成像时长为t2,对应轨迹条带2。

(4)卫星反方向俯仰机动，经过时长t3回头至俯仰角-θ。

(5)保持俯仰角-θ“回头看”，成像时长t2,对应轨迹条带3。

2.2立体成像条带长度通用公式分析

从图1可以看出，圆形地球模型下的立体成像条带长度如下。

Lcirc=Re·ωet2

(1)

式中：轨道角速度ωe由式(2)确定。

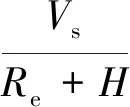
(2)

式中：卫星飞行速度Vs由式(3)确定。

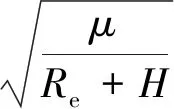
(3)

式中：μ为地球引力常数。

图1中相关的几个角度存在式(4)所示关系。其中，φ1，φ2分别表示θ1，θ2所对应的地心张角，由式(5)和式(6)确定。

ωet2=φ1+φ2-ωet3

(4)

(5)

(6)

综上，可将Lcirc重新定义如下。

(7)

可以看出，立体成像条带长度与轨道高度、2次观测俯仰角、反方向俯仰机动时间相关。在反方向俯仰机动时间确定时，2次观测俯仰角绝对值增加，对应的地心张角也越大，可获取的立体成像条带长度越大；而2次观测俯仰角确定时，减少反方向俯仰机动时间，也就是提高卫星姿态机动能力，也可获取更大的立体成像条带长度。

2.3立体成像对卫星姿态机动能力需求分析

双视立体成像时，令第1次成像对应俯仰角θ1=θ(θ>0)，第2次成像对应俯仰角-θ(θ2=θ)，则可将式(7)重写为式(8)。其中，Lcirc_2D表示圆形地球模型下的双视立体成像条带长度，t3(Δθ=2θ)表示俯仰角变化2θ对应的姿态机动时间。

(8)

三视立体成像时，令第1次成像对应俯仰角θ1=θ，第2次成像对应俯仰角θ2=0，则可将式(7)重写为式(9)。其中，Lcirc_3D表示圆形地球模型下的三视立体成像条带长度，t3(Δθ=θ)表示俯仰角变化θ对应的姿态机动时间。

(9)

需要注意的是，虽然式(7)中观测视角切换过程所需时间均定义为t3，但由于双视立体成像和三视立体成像对应的卫星俯仰方向的机动角度差别，实际上该时间也是有差别的。

立体成像时，基高比定义为基线长度与轨道高度之比，该指标对高程精度有较大影响。文献[15]中对圆形地球模型下的基高比计算公式进行了推导，得到一种典型的表达方式。根据定义，容易推导出基高比BH的另一种公式定义，见式(10)，无量纲。

(10)

根据式(10)，可将式(8)和式(9)分别重写为式(11)和式(12)。

(11)

(12)

令双视立体成像和三视立体成像所允许最长机动时间(对应成像条带长度为0)分别为t3(Δθ=2θ)th和t3(Δθ=θ)th，卫星实际的机动时间分别为t3(Δθ=2θ)real和t3(Δθ=θ)real，则可将式(11)和式(12)重写为式(13)和式(14)。

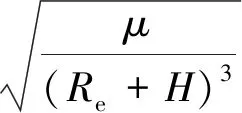
(t3(Δθ=2θ)th-t3(Δθ=2θ)real)

(13)

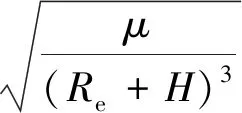
(t3(Δθ=θ)th-t3(Δθ=θ)real)

(14)

特定轨道高度和基高比下，立体成像所允许最长机动时间(门限值)为确定值。从式(13)和式(14)可以看出：对双视立体成像而言，存在唯一的变量t3(Δθ=2θ)real来决定双视立体成像条带长度Lcirc_2D；对三视立体成像而言，也存在唯一的变量t3(Δθ=θ)real来决定三视立体成像条带长度Lcirc_3D。根据不同的立体成像条带长度需求，可由式(13)和式(14)反算出对卫星姿态机动能力的实际需求。

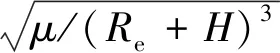
Lcirc_2D=Ve·(t3(Δθ=2θ)th-t3(Δθ=2θ)real)

(15)

Lcirc_3D=Ve·(t3(Δθ=θ)th-t3(Δθ=θ)real)

(16)

以500 km圆轨道为例，Ve≈7 km/s，从式(15)和式(16)容易看出，实际的机动时间t3(Δθ=2θ)real和t3(Δθ=θ)real每减少1 s，所获取立体成像条带长度可增加约7 km。

3 实际应用分析

3.1立体成像覆盖能力分析

某卫星的典型姿态机动能力如表1所示。对于其他机动角度所对应的机动时间，可在表1所示两点之间采用线性插值进行简化估算。根据该机动能力，可以获取圆形地球模型下的双视立体、三视立体条带长度如图2所示。其中，俯仰预置角指前视、后视成像对应的卫星俯仰角绝对值。以俯仰预置角30°为例，双视立体成像时，首先前视(“抬头看”)对应俯仰角为+30°，然后后视(“回头看”)对应俯仰角为-30°，2个角度观测共需要卫星在俯仰方向机动60°，用时为50 s；三视立体成像时，首先前视(“抬头看”)对应俯仰角为+30°，然后正视(“向下看”)对应俯仰角为0°，最后后视(“回头看”)对应俯仰角为-30°，前视至正视观测、正视至后视观测均需要卫星在俯仰方向机动30°，用时为35 s。

表1 典型姿态机动能力

由图2可以看出：

(1)其他条件相同时，双视立体成像条带长度大于三视立体成像条带长度。

(2)其他条件相同时，俯仰预置角越大，可获取的立体成像条带长度越大。

(3)其他条件相同时，抬高轨道高度，有利于增加立体成像条带长度。

(4)此典型姿态机动能力略显不足，尤其是在轨道高度500 km、较小的俯仰预置角条件下，三视立体成像获取条带长度小于0，即不能完成立体成像任务。因此，有必要进一步提升卫星姿态机动能力，以满足立体成像需求。

从式(8)、式(9)可以看出，假设卫星姿态机动速度无限快，即t3(Δθ=2θ)和t3(Δθ=θ)为0(实际上均应大于0)，此时，对双视立体成像和三视立体成像而言，所获取的条带长度为最大值，如图3所示。从图3可以看出，轨道高度增加和俯仰预置角增加，均会带来立体成像条带长度最大值的增加。以轨道高度500 km、俯仰预置角25°为例，双视立体成像和三视立体成像可获取的最大条带长度分别为470.4 km和235.2 km，但专用立体成像测绘卫星却可以通过相机长时间开机成像获取很大的条带长度(如连续成像15 min可获取约6000 km条带)，两者成像覆盖能力差别较大。

在上述分析中，并未考虑敏捷卫星完成第1个条带立体成像后，可以不断重复第2.1节中的几个步骤，继续获取后续第2个条带、第3个条带……在卫星姿态机动速度无限快，即t3(Δθ=2θ)为0的情况下，由图1可推导出连续多次双视立体成像如图4所示，其中φ表示θ所对应的地心张角。图4中存在很多相同的三角形，2次立体成像条带之间的漏缝长度，与单个立体条带长度相同。而双线阵测绘卫星可连续成像，对其漏缝也可成像，也就是说，极限情况下，敏捷卫星双视立体成像可获取的条带长度约占专用双线阵测绘卫星的1/2。实际上，由于俯仰方向的姿态机动需要耗费一定时间，以表1中数据为例，机动50°耗时45 s，敏捷卫星双视立体成像所获取的条带长度实际为152.8 km，相比图3中470.4 km大幅度减小(仅约为32.5%)；再考虑相邻2个条带切换过程所需时间，中间漏缝进一步增加(比470.4 km更大，增加量为45 s对应的星下点移动量317.6 km)。由此，可推算出敏捷卫星双视立体成像的覆盖能力仅为双线阵测绘卫星的12.1%。

与上述分析过程相似，卫星姿态机动速度无限快，即t3(Δθ=θ)为0的极限情况下，敏捷卫星三视立体成像可获取的条带长度约占专用三线阵测绘卫星的1/3。实际上，由于俯仰方向的姿态机动需要耗费一定时间，以表1中数据为例，机动25°耗时30 s，敏捷卫星三视立体成像所获取的条带长度实际为23.5 km，相比图3中235.2 km大幅度减小(仅约为10%)。再考虑相邻2个条带切换过程所需时间，中间漏缝进一步增加(比235.2 km更大，增加量为30 s对应的星下点移动量211.7 km)。由此，可推算出敏捷卫星三视立体成像的覆盖能力仅为三线阵测绘卫星的3.4%。

3.2基高比为1时姿态机动能力分析

根据摄影测量原理，当基高比接近1时，立体图像处理效果较好，可选择合适的观测视角，以获取较好的立体成像效果[2]。由式(10)可知，基高比为1时，每个轨道高度H对应唯一的俯仰预置角，可以解算出其对应关系，如图5所示。综合考虑大气阻力、相机分辨率等因素，敏捷卫星轨道高度通常不会低于400 km，也不会高于1000 km。由图5可以看出，基高比为1、轨道高度在400～1000 km时，对应的俯仰预置角在23.07°～25.04°，且随着轨道高度的增加而减小。

为满足立体成像需求，式(11)和式(12)需大于0。当基高比为1时，可得到不同轨道高度下对姿态机动能力的最小需求(对应于最长的机动时间)如图6所示。由图6可以看出：

(1)轨道高度相同时，双视立体成像的俯仰机动角、所允许的最长机动时间均为三视立体成像的2倍。

(2)对双视立体成像和三视立体成像而言，随着轨道高度增加，俯仰机动角减小，同时，对允许的最长机动时间却增大，因此轨道高度增加将降低对卫星姿态机动能力的需求。

(3)以500 km典型轨道高度为例，双视立体成像需机动49.38°，允许最长机动时间为65.70 s；三视立体成像需机动24.69°，允许最长机动时间为32.85 s，其平均机动角速度为0.75(°)/s。考虑到卫星在轨进行姿态机动时，必然存在加速、减速及稳定的过程，这些过程会降低卫星的平均机动角速度，因此，卫星的最大机动角速度必须大于0.75(°)/s，其具体数值要根据卫星的姿态机动路径规划曲线确定。

4 结论

本文通过对敏捷卫星立体成像覆盖能力的分析，得出如下结论。

(1)与专用立体成像测绘的多线阵卫星可连续长条带立体成像不同，敏捷卫星要依靠俯仰方向姿态机动来实现立体成像，可对重点区域目标进行观测，但难以实现长条带立体成像。其成像条带长度与俯仰预置角、姿态机动能力、立体观测视角数量等因素密切相关。姿态机动速度无限快的理想情况下，敏捷卫星的双视立体成像和三视立体成像覆盖能力，仅为专用双线阵和三线阵测绘卫星的1/2和1/3，且实际覆盖能力远小于该数据。

(2)为提高立体成像覆盖能力，应尽可能提高敏捷卫星姿态机动能力，缩短姿态机动时间。以500 km典型圆轨道为例，每减少1 s姿态机动时间，立体成像条带长度可增加约7 km。

References)

[1] 余婧，喜进军，于龙江，等.敏捷卫星同轨多条带拼幅成像模式研究[J].航天器工程，2015，24(2)：27-34

Yu Jing, Xi Jinjun, Yu Longjiang, et al. Study of one-orbit multi-stripes splicing imaging for agile satellite [J]. Spacecraft Engineering, 2015, 24(2): 27-34 (in Chinese)

[2] 张新伟，戴君，刘付强.敏捷遥感卫星工作模式研究[J].航天器工程，2011，20(4)：35-37

Zhang Xinwei, Dai Jun, Liu Fuqiang. Research on working mode of remote sensing satellite with agile attitude control [J]. Spacecraft Engineering, 2011, 20(4): 35-37 (in Chinese)

[3] Thierry T. Comparison of stereo-extracted DTM from different high resolution sensors [J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10)： 2121-2129

[4] 田原，王密.基于步进搜索的敏捷同轨立体成像规划[J].无线电工程，2015，45(11)：44-47，51

Tian Yuan, Wang Mi. An optimal imaging-scheduling algorithm for stereo acquisition mode of agile satellite based on step-size search [J]. Radio Engineering, 2015， 45(11)： 44-47, 51 (in Chinese)

[5] Lindeberg T. Detecting salient blob-like image structures and their scales with a scale-space primal sketch: a method of focus-of-attention [J]. International Journal of Computer Vision, 1993, 11(3)： 283-318

[6] Wie B. Singularity escape/avoidance steering logic for control moment gyro systems [J]. Journal of Guidance Control and Dynamics, 2005, 28(5): 948-956

[7] 王淑一，魏春岭，刘其睿.敏捷卫星快速姿态机动方法研究[J].空间控制技术与应用，2011，37(4)：36-40

Wang Shuyi， Wei Chunling， Liu Qirui. A quick attitude maneuver algorithm for agile satellites [J]. Aerospace Control and Application, 2011, 37(4): 36-40 (in Chinese)

[8] 叶东.敏捷卫星姿态快速机动与稳定控制方法研究[D].哈尔滨：哈尔滨工业大学，2013

Ye Dong. Research on fast maneuver and stabilization control algorithm for agile satellite [D]. Harbin: Harbin Institute of Technology, 2013 (in Chinese)

[9] 何昱.基于单框架控制力矩陀螺的敏捷小卫星姿态机动控制研究[D].哈尔滨：哈尔滨工业大学，2011

He Yu. Research on attitude maneuvers control of SGCMG based agile small satellite [D]. Harbin: Harbin Institute of Technology, 2011 (in Chinese)

[10] 孙凯，白国庆，陈英武，等.面向动作序列的敏捷卫星任务规划问题[J].国防科技大学学报，2012，34(6)：141-147

Sun Kai, Bai Guoqing, Chen Yingwu, et al. Action planning for agile earth-observing satellite mission planning problem [J]. Journal of National University of Defense Technology, 2012, 34(6): 141-147 (in Chinese)

[11] 刘嵩，陈英武.敏捷成像卫星自主任务规划模型与算法[J].国防科技大学学报，2015，37(6)：96-102

Liu Song, Chen Yingwu. Model and algorithm of automatic planning for agile imaging satellite [J]. Journal of National University of Defense Technology, 2015, 37(6): 96-102 (in Chinese)

[12] 章登义，郭雷，王骞，等.一种面向区域目标的敏捷成像卫星单轨调度方法[J].武汉大学学报(信息科学版)，2014，39(8)：901-906

Zhang Dengyi, Guo Lei, Wang Qian, et al. An improved single-orbit scheduling method for agile imaging satellite towards area target [J]. Geomatics and Information Science of Wuhan University, 2014, 39(8): 901-906 (in Chinese)

[13] 阮启明，谭跃进，李菊方，等.对地观测卫星的区域目标分割与优选问题研究[J].测绘学报，2006，31(1)：98-100

Ruan Qiming, Tan Yuejin, Li Jufang, et al. Research on segmenting and selecting of area targets [J]. Science of Surveying and Mapping, 2006, 31(1): 98-100 (in Chinese)

[14] 曹海翊，刘希刚，李少辉，等.“资源三号”卫星遥感技术[J].航天返回与遥感，2012，33(3)：7-16

Cao Haiyi, Liu Xigang, Li Shaohui, et al. ZY-3 satellite remote sensing technology [J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 7-16 (in Chinese)

[15] 周胜利.三线阵TDICCD在测图卫星中的应用分析[J].航天器工程，2007，16(4)：19-22

Zhou Shengli. Analysis of three-linear TDICCD array application in cartography satellite [J]. Spacecraft Engineering, 2007, 16(4): 19-22 (in Chinese)

Analysis on Stereo Mapping Coverage Ability of Agile Satellite

WANG Zhongguo LI Zhen TANG Haitao LU Fan TIAN Zhixin LI Jindong

(Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)

The coverage ability of agile satellite only depends on mapping strip length when swath is determined. According to the stereo mapping process of agile satellite, the general equation of stereo mapping strip length based circular earth model and satellite ground track is deduced, the minimum maneuver ability requirement of agile satellite for stereo mapping is analyzed, and the general equations of attitude maneuver ability requirement for stereo mapping strip length are deduced. Based on typical attitude maneuver ability of some satellite, one application is analyzed, and the effective rules of orbital altitude, preset pitch angle and stereo mapping angel number are obtained. Simulation results show that the increase of orbital altitude and preset pitch angle will result in the increase of stereo mapping strip length with the same other conditions, and the strip length of double-view stereo mapping is longer than three-view stereo mapping. The analysis method and the formula in this paper can provide a reference for system analysis and design of agile satellite.

agile satellite； stereo mapping； coverage ability； strip length； attitude maneuver ability

V474.2

A

10.3969/j.issn.1673-8748.2017.04.002

2017-06-19；

2017-07-19

国家重大航天工程

王中果，男，硕士，高级工程师，从事低轨遥感卫星总体设计工作。Email：wang_zhongguo@sohu.com。

(编辑：夏光)