太阳翼不同转角的卫星在轨模态频率计算方法

向明江 李梦宇 吕旺,3 杜继超

(1 上海卫星工程研究所，上海 201109)(2 上海航天技术研究院，上海 201109)(3 清华大学航天航空学院，北京 100084)(4湖北三江航天红峰控制有限公司，湖北孝感 432000)

太阳翼不同转角的卫星在轨模态频率计算方法

向明江1李梦宇2吕旺1,3杜继超4

(1 上海卫星工程研究所，上海 201109)(2 上海航天技术研究院，上海 201109)(3 清华大学航天航空学院，北京 100084)(4湖北三江航天红峰控制有限公司，湖北孝感 432000)

卫星挠性振动频率会随着太阳翼的转动发生变化，在卫星动力学频率规划设计时尤其需要考虑到,以避免发生耦合振动。文章针对具有太阳翼的卫星，研究了太阳翼转动时由于星体构型变化对卫星模态频率产生的影响。通过建立卫星动力学混合坐标方程，推演出卫星结构动力学特征方程，在太阳翼转到不同角度时对卫星系统模态进行解算，从而获得一种具有太阳翼的遥感卫星系统模态计算方法。以某遥感卫星为背景进行了在轨模态计算，并与该卫星陀螺姿态角速度遥测数据对比，误差小于10%，验证了在轨模态计算方法的准确性。

太阳翼；挠性振动；在轨模态；频率计算

1 引 言

一般卫星通常安装有太阳翼、天线等挠性附件，且具有飞轮、驱动机构、有效载荷等周期性转动部件。近年来卫星在轨出现过转动部件与挠性附件的耦合共振问题，严重影响了卫星的姿态稳定度，使得有效载荷无法正常工作。在轨耦合振动问题需要引起高度重视，在卫星研制阶段开展卫星动力学频谱规划设计成为一项必不可少的工作。

在文献[1]中可以看出，目前在卫星工程中，对于具有太阳翼的卫星在轨振动频率，常以标称值的形式给出前几阶模态频率，设计者据此开展转动部件与挠性附件的频率隔离规划设计。这存在两个问题：如果以给出的标称频率值的作为频谱规划的输入，很容易引发耦合共振问题，因为在太阳翼转动时，卫星在轨振动频率是随时变化的。如果在标称频率值附近规划一个误差区间，这存在如何选取误差区间的问题，误差区间选取太小，仍有可能发生在轨耦合振动；误差区间选取太大，有可能使有效载荷、飞轮等转动部件没有合适的工作频率范围，进而需要对转动部件或者太阳翼作出更改，造成不必要的浪费。因此，合理的动力学频谱规划和控制系统设计，要求提供准确的卫星在轨振动频率，尤其对于具有太阳翼等挠性附件的卫星，需要提供准确的振动频率范围，而不是一个标称值。

对于所有具有挠性附件的卫星，在轨振动频率为非约束模态频率，与地面约束模态频率不同，这在很多文献中已有阐述。文献[2]给出了采用混合坐标法计算挠性航天器系统频率，文献[3]给出挠性卫星在轨非约束模态计算方法，文献[4-8]对带挠性太阳翼的卫星动力学进行了建模与仿真分析，但都是针对卫星在某些固定构型的情况，并未对太阳翼转动到不同角度时的变化规律展开分析。

通常可以获得在地面固支约束下比较准确的太阳翼固有模态频率，本文以此为输入，从混合坐标方程出发，通过合理简化得到卫星在轨线性振动方程，求解方程特征值可以得到卫星在轨振动频率。将太阳翼转动角度设为自变量，覆盖全部转动角度范围，可求得太阳翼不同转角时的卫星在轨振动模态频率，为卫星动力学频谱规划和控制系统设计提供比较准确的输入。

2 具有太阳翼的卫星动力学建模

具有单个太阳翼的卫星构型如图1所示，坐标系定义如下：卫星布局系XLYLZL是根据布局和装配的需求，以卫星上特定点和与卫星几何构型相关的方向定义的；整星坐标系XsYsZs与星体固连运动，原点在整星质心Os，坐标轴与布局系平行；卫星本体系XbYbZb与星本体固连运动，原点在本体质心Ob，坐标轴与布局系平行；太阳翼系XaYaZa与太阳翼固连运动，原点在安装点Oa，相对于星体系+Y轴按右手方向转过的角度为θ，当太阳翼转角θ=0°时坐标轴与卫星系平行。

图1 具有单个挠性太阳翼的卫星构型示意图Fig.1 Configuration of a satellite with one rotatable flexible solar wing

卫星系到太阳翼系的转换关系矩阵可描述为

(1)

卫星本体质量为mb，相对于其质心在卫星本体系下描述的惯量矩阵为Jb；太阳翼质量为ma，相对于其质心在太阳翼系下描述的惯量矩阵为Ja，卫星整星质量为ms，相对于卫星质心在卫星坐标系下描述的惯量矩阵为Js(随太阳翼转动发生变化)。利用拉格朗日法在卫星坐标系下建立挠性卫星动力学混合坐标方程为

(2)

式中：方程变量v、ω和η，分别为卫星质心平移线速度、卫星绕质心转动角速度和太阳翼模态坐标；ω×代表ω的叉乘矩阵；Ω为太阳翼约束模态频率对角矩阵；ζ为太阳翼振动的阻尼比对角矩阵；Bt和Br分别为太阳翼相对于卫星质心的平动和转动耦合系数；F、T分别为外部力学环境的合力和合力矩。随着太阳翼转动，Js、Bt和Br将随太阳翼转动发生变化，除变量v、ω和η以外的其他量保持定常。

3 卫星在轨模态变化规律分析

在小幅振动情况下，卫星在轨模态是卫星的固有特性，与外部环境作用无关，可忽略方程组中的外干扰力F和力矩T；挠性振动对星体角速度影响较小，角速度ω视为一阶小量，卫星陀螺力矩项作为角速度的二阶小量可忽略。方程组(2)变为

(3)

将方程组(3)前两式代入第三式，得到以模态坐标η为变量的卫星系统结构动力学方程：

(4)

式中：E为单位阵；Bt和Br为太阳翼的耦合系数。

(5)

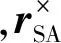
式(4)中的Js为卫星惯量在卫星系投影。

Js=Jb+Ib+AbaJaAab+Ia

(6)

式中：Ib和Ia分别为太阳翼和星本体在其质心处的集中质量相对卫星系的转动惯量。

(7)

式中：rSB为卫星质心到星本体质心的矢量在卫星系分量；rSC为卫星质心到太阳翼质心的矢量在卫星系分量。

由于太阳翼质心不一定在转轴延长线上，转动时卫星质心也会存在微小变化，故与卫星质心相关的rSA、rSB和rSC均随太阳翼转动发生变化，当太阳翼质心离转轴距离较近时，太阳翼转动对卫星质心的影响可忽略，则这3项可视为常量。

对式(4)采用拉氏变换处理后，得到卫星结构动力学特征方程：

(8)

当θ取值从0°～360°时，得到相应的Js、Bt和Br，代入式(8)求解特征值，即得到与太阳翼转动角度相关的各阶卫星系统模态频率。

4 计算实例

某安装单个太阳翼的太阳同步轨道遥感卫星构型与图1类似，质量特性参数如表1所示。

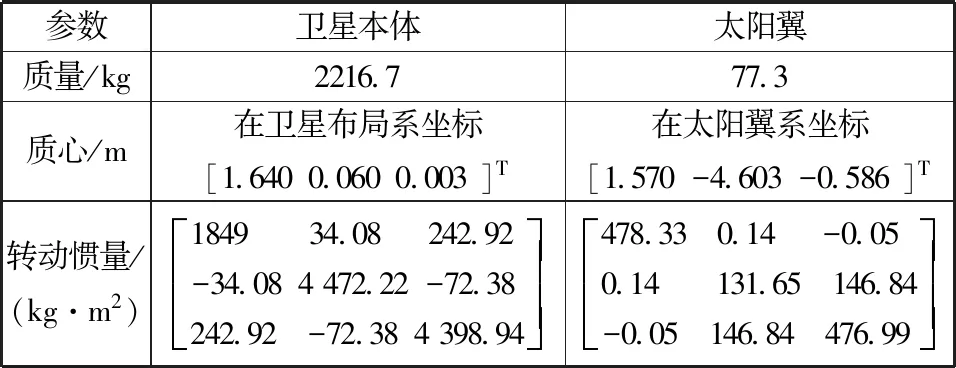
表1 卫星质量特性参数

太阳翼约束模态固有频率、阻尼和相对于安装点的平动耦合系数、转动耦合系数，如表2所示。挠性太阳翼约束模态前4阶振型见图2。太阳翼系原点在布局系坐标(m)为[1.570-1.000-0.723]T。

表2 太阳翼挠性参数(前4阶)

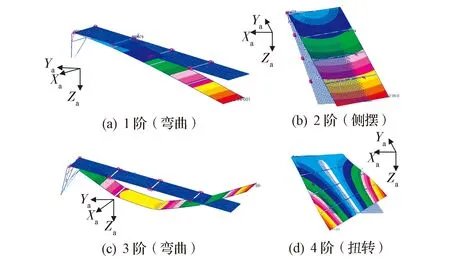
图2 太阳翼振型图(前4阶)Fig.2 Illustrations of the solar wing mode shape ( previous 4 orders)

从振型图像和耦合系数数据可以看出各阶振型对星体的影响形式：①1阶模态为弯曲基频，Za方向的平动和Xa方向的转动为耦合的主要分量；②2阶模态为侧摆基频，Xa方向的平动和Za方向的转动为耦合的主要分量；③3阶模态为弯曲次阶，Ya方向的平动和Xa方向的转动为耦合的主要分量；④4阶模态为扭转基频，Xa方向的平动和Ya方向的转动为耦合的主要分量。

当太阳翼转到不同角度时，其挠性特性对卫星本体系的耦合作用也随之变化。将表1和表2数据代入式(8)求解特征方程，太阳翼转角从1°～360°每隔1°进行一次特征值求解，形成卫星系统模态频率前4阶变化曲线如图3所示。

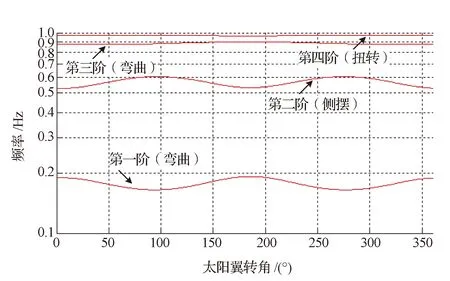
图3 卫星系统模态频率变化曲线Fig.3 Satellite mode frequencies variation diagram

从图3可以看出，1、2阶卫星系统模态频率分别对应太阳翼弯曲、侧摆的基频。由于星体在X和Z轴方向的惯量差距较大，随着太阳翼转动一周，1、2阶卫星系统模态呈现2个周期的波动；第3阶模态波动形式与1阶相同，但由于其耦合系数较小，频率波动幅度不明显；第4阶卫星系统模态由太阳翼扭转模态引起，由于太阳翼转动过程中卫星Y方向惯量变化较小，对应的卫星系统模态近似恒定不变。

5 与卫星在轨遥测数据对比的验证

该卫星在发射后入轨初期进行了轨道修正，在调轨道的前后期间都采用了喷气斜开关线姿态控制方式。姿态推力器喷气会引起太阳翼挠性振动(图4)，导致星体角速度发生变化(图5)，相当于对卫星动力学系统的随机扰动。太阳翼通过安装点与卫星本体相连，太阳翼在轨挠性振动会传递到星本体，引起星本体姿态角速度同步抖动，因此，通过处理星上陀螺测量的卫星本体角速度数据，可以间接识别出太阳翼挠性振动响应特征。

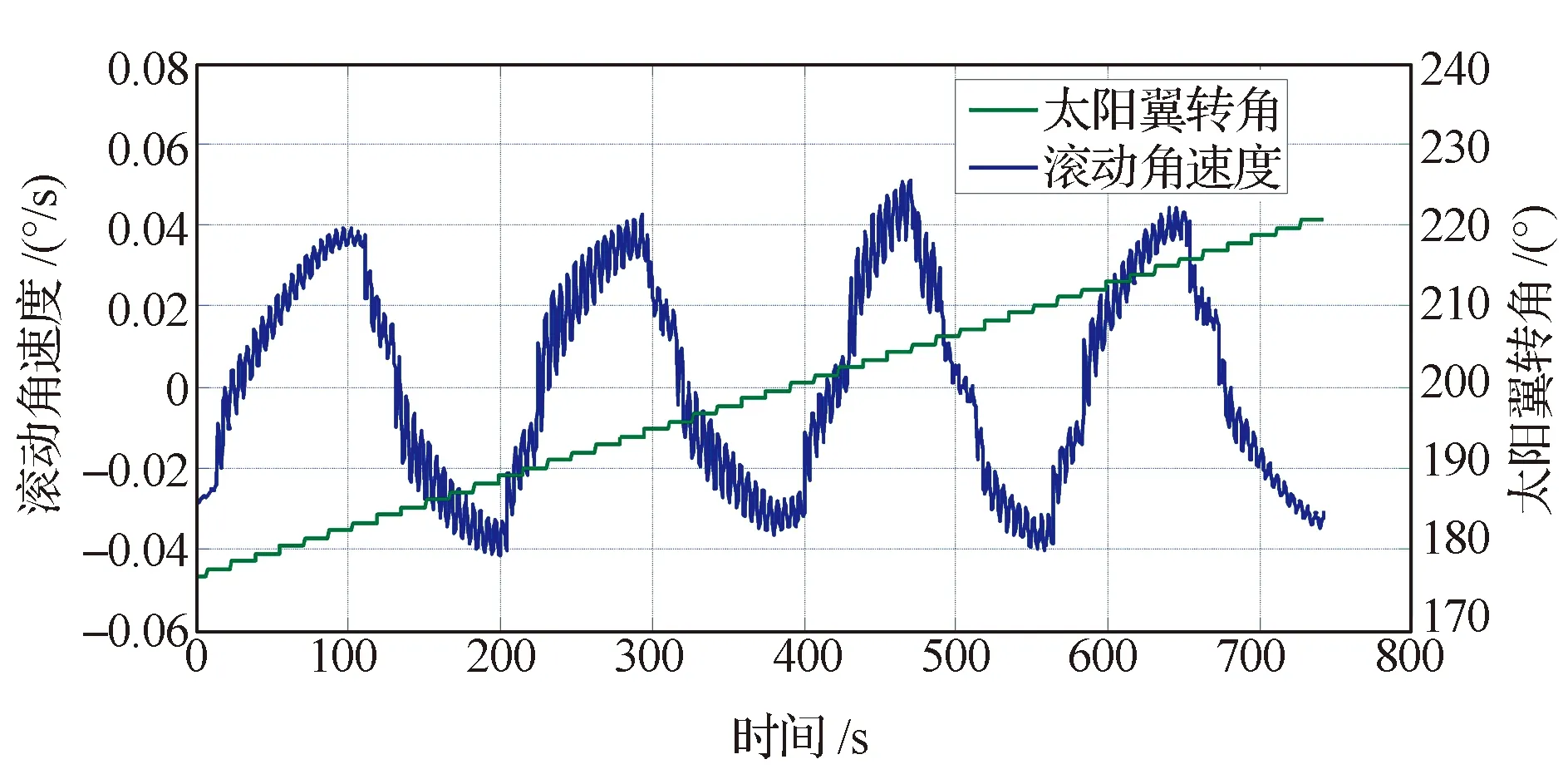
图4 姿态推力器喷气激起太阳翼挠性振动Fig.4 Flexible vibration caused by thruster jet

对遥测数据进行频域特性分析。从接入喷气开始每100 s数据对姿态角速度数据进行一次快速傅里叶变换。将所有傅里叶频域曲线并排可以分析出太阳翼相对星体不同角度时卫星系统结构动力学响应特性，轨道控制时如图6所示，可见，当太阳翼转到40°(图6中坐标为400°)附近时进行了轨控喷气，在各个频段上均有较大响应，随后太阳翼进行了快速驱动。

将算例中的理论分析结果与在轨遥测数据分析结果对比如图7～9和表3所示。图6～9中，当太阳翼位于某转角时，对某频率成分激励的动力学响应越大，则颜色偏红；反之则偏蓝。

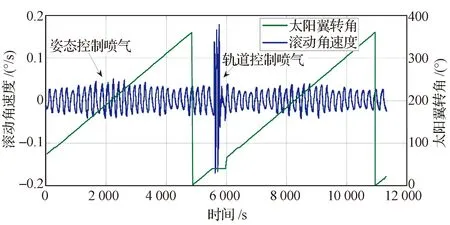
图5 卫星在轨滚动角速度Fig.5 On-orbit rolling angular velocity of satellite

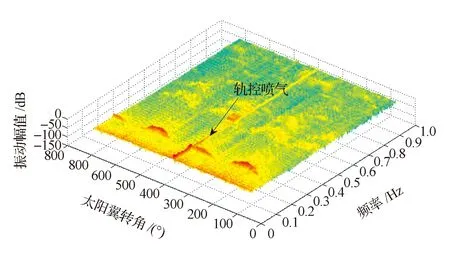
图6 太阳翼转动期间卫星结构动力学响应Fig.6 The structure dynamic response of satellite duringsolar wing rotation

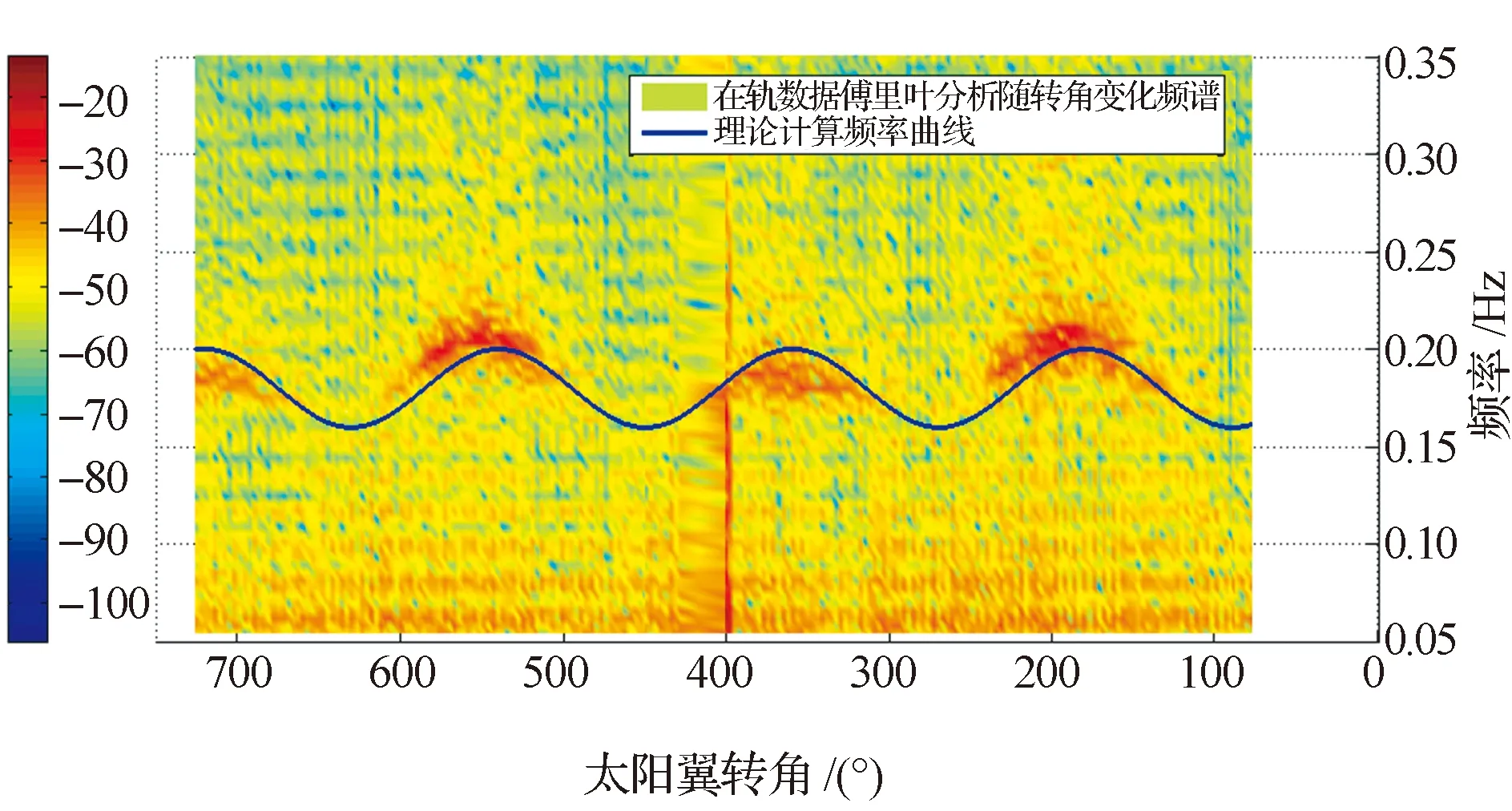
图7 卫星系统模态1阶(太阳翼弯曲)频率对比Fig.7 Comparison of satellite 1st order mode frequencies (solar wing bending)

从对比结果可知，太阳翼弯曲1阶和侧摆1阶模态对应的卫星基频计算结果与在轨数据的符合性较好；在有限元建模中太阳翼弯曲2阶模态频率的计算精度受1阶影响很大，可能高于遥测采样频带，在频率结果中未体现；太阳翼扭转1阶模态误差较大，可能包含地面模态测试和有限元建模误差。但太阳翼弯曲2阶和扭转1阶模态的耦合系数均较小，其对卫星姿态稳定度影响有限。

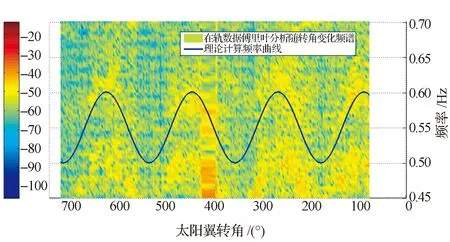
图8 卫星系统模态2阶(太阳翼侧摆)频率对比Fig.8 Comparison of satellite 2nd order mode frequencies (solar wing swaying)

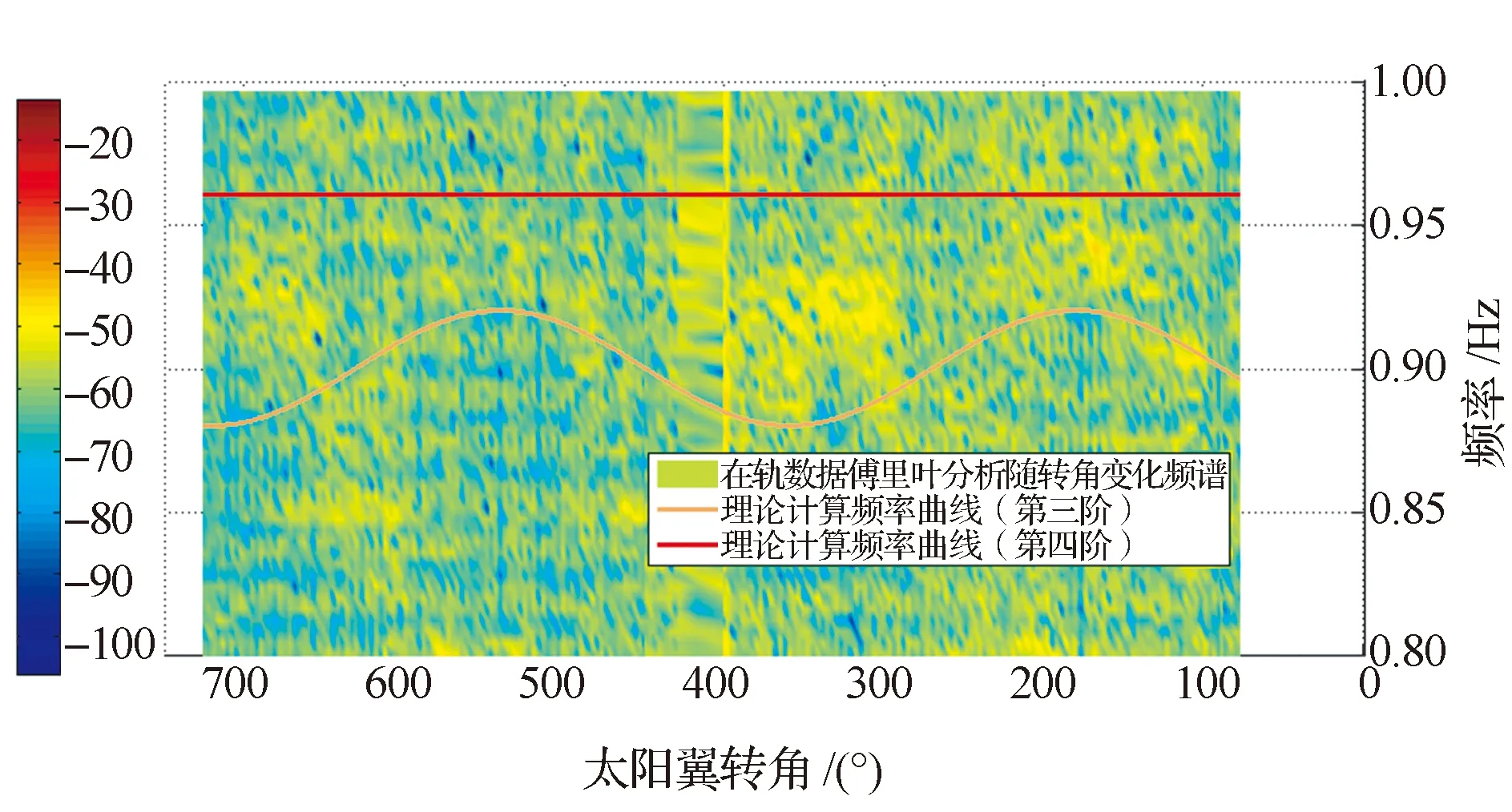
图9 卫星系统模态3，4阶(太阳翼扭转)频率对比Fig.9 Comparison of satellite 3rd/4th order mode frequencies (solar wing twisting)

表3 卫星在轨模态频率与计算结果对比汇总表

6 结论

本文针对具有挠性太阳翼的卫星挠性动力学进行了研究。利用卫星动力学混合坐标方程推演出卫星结构动力学特征方程，从而给出了太阳翼在不同转角时卫星在轨模态频率的计算方法。以某单太阳翼遥感卫星为例进行了在轨模态频率计算，频率值随着太阳翼转动按照正(余)弦规律变化。通过卫星遥测数据分析结果与卫星基频计算结果的对比，对姿态稳定度影响比较大的太阳翼弯曲和侧摆基频对应的卫星模态，其太阳翼不同角度时的计算相对误差分别为6.2%和1.9%，验证了具有太阳翼的卫星在轨模态频率计算方法的准确性，可以为整星动力学频谱规划提供比较准确的输入条件。

References)

[1] 吕旺, 向明江, 沈毅力, 等. 遥感卫星动力学频谱规划[J]. 空间控制技术与应用, 2015, 41(2): 12-17

Lyu Wang, Xiang Mingjiang, Shen Yili, et al. Dynamic frequency spectrum planning of remote sensing satellite[J]. Aerospace Control and Application, 2015, 41(2): 12-17 (in Chinese)

[2] 缪炳祺, 曲广吉, 夏邃勤．柔性航天器的模态综合-混合坐标动力学建模[J]. 浙江工业大学学报, 2002, 30(2): 139-152

Miao Bingqi, Qu Guangji, Xia Suiqin. Modal synthesis-hybrid coordinate dynamics modeling of flexible spacecrafts[J]. Journal of Zhejiang University of Technology, 2002, 30(2): 139-152 (in Chinese)

[3] 吕旺, 向明江, 叶文郁, 等．挠性卫星在轨非约束模态计算研究[J]. 宇航学报, 2014, 35(4): 404-409

Lyu Wang, Xiang Mingjiang, Ye Wenyu, et al. Research on calculation of on-orbit unconstrained mode of flexible satellite[J]. Journal of Astronautics, 2014, 35(4): 404-409 (in Chinese)

[4] 王天舒, 孔宪仁, 王本利, 等. 变拓扑航天器附件展开动力学的全局仿真[J]. 哈尔滨工业大学学报, 2000(3): 4-7

Wang Tianshu, Kong Xianren, Wang Benli, et al. Global simulation of spacecraft appendage deployment dynamics by variable topology[J]. Journal of Harbin Institute of Technology, 2000(3): 4-7 (in Chinese)

[5] 刘墩，杨大明. 带挠性附件卫星的模型化及截断[J]. 宇航学报, 1989, 10(4): 87-95

Liu Tun, Yang Daming. Modeling of spacecraft with flexible appendages and model truncation[J]. Journal of Astronautics, 1989, 10(4): 87-95 (in Chinese)

[6] 刘莹莹，周军. 挠性多体航天器姿态动力学建模与分析[J]. 飞行力学, 2005, 23(3): 60-63

Liu Yingying, Zhou Jun. Dynamics modeling and analysis for a flexible multi-body[J]. Spacecraft Flight Dynamics, 2005, 23(3): 60-63 (in Chinese)

[7] 李俊峰，王照林. 带挠性仲展附件的航天器姿态动力学研究[J]. 清华大学学报(自然科学版), 1996, 36(10): 35-40

Li Junfeng, Wang Zhaolin. Attitude dynamics of a spacecraft with deploying flexible appendages[J]. Journal of Tsinghua University (Sci & Tech), 1996, 36(10): 35-40 (in Chinese)

[8] P W Likins. Dynamics and control of flexible space vehicles，32-1329[R]．Washington D.C.: NASA, 1970

On-orbit Mode Frequencies Computing Method of Satellite with Different Rotational Angles of Solar Wing

XIANG Mingjiang1LI Mengyu2LYU Wang1,3DU Jichao4

(1 Shanghai Institute of Satellite Engineering, Shanghai 201109, China)(2 Shanghai Academy of Spaceflight Technology, Shanghai 201109, China)(3 School of Aerospace, Tsinghua University, Beijing 100084, China)(4 Hong Feng Control Co. Ltd. of Sanjiang Aerospace Corp, Xiaogan, Hubei 432000, China)

The flexible vibration frequency of the satellite changes with rotation of the solar wing, it is important to avoid resonance especially in the dynamics frequency planning. In this paper, the flexible dynamics of satellite with rotatable solar wing is researched, and the change of the satellite mode frequencies affected by the configuration variation is studied. Firstly, the hybrid coordinate equations of flexible dynamics of satellite are given to deduct the structural dynamics equations of the whole satellite. Secondly, the characteristis equation of the on-orbit modes is given, then the satellite mode frequencies are solved for every rotational angle of solar wing. Finally, a remote sensing satellite is taken for example to verify the accuracy of the method by compare the on-orbit data with the computing result.

solar wing; flexible vibration; on-orbit modes; frequency calculation

V412.4

A

10.3969/j.issn.1673-8748.2017.04.006

2017-04-25；

2017-07-19

向明江，男，工程师，研究方向为航天器动力学与控制技术。Email: okboy129214@sina.com。

(编辑：张小琳)