半无限大体中次表面裂纹间的相互影响

张言库， 杨鸿达， 昝晓东， 刑帅兵， 江晓禹

(西南交通大学 力学与工程学院， 成都 610031)

半无限大体中次表面裂纹间的相互影响

张言库， 杨鸿达， 昝晓东， 刑帅兵， 江晓禹

(西南交通大学 力学与工程学院， 成都 610031)

针对钢轨次表面的微裂纹问题，采用含裂纹的半无限大体进行简化，研究了半无限大体中裂纹间的相互影响。利用弹性力学中半平面体在边界上受法向分布力的应力公式求出裂纹面上的应力，并采用Kachanov简化方法，得到了裂纹尖端的应力强度因子。分析了裂纹与表面的距离、裂纹尺寸和裂纹之间的距离对裂纹尖端应力强度因子的影响。结果表明：裂纹与表面的距离越大裂纹间的影响越小，裂纹尺寸越大裂纹间的影响越大，裂纹之间的距离越大裂纹间的影响越小。

应力强度因子；半无限大体；裂纹

钢轨在铁路运输中起着支撑作用。近年来，铁路运输向着高速、重载以及高密度使用的方向发展。随着中国铁路运行速度的提高，钢轨表面的破坏越来越严重[1]，这些破坏会对列车的行车安全造成危害。钢轨的破坏很大程度上是因为钢轨次表面产生裂纹，由于车轮对钢轨的循环力作用使得钢轨次表面产生微裂纹，随着微裂纹扩展到一定程度会导致钢轨剥离甚至产生断裂。研究钢轨次表面的裂纹能更好地了解微裂纹的规律，更加清晰地认识钢轨的疲劳断裂机理，对铁路钢轨维护起到强有力的助推作用。这也是裂纹问题一直得到广大学者持续关注的根本原因所在。

针对裂纹问题很多专家学者进行了研究[2-14]。闫相桥[2]利用一种边界元方法来研究有限长主裂纹与微裂纹的相互作用。夏晓舟等[3]研究不同裂纹布置带来的屏蔽和增强效应。王恒等[4]用扩展有限元的方法研究了微裂纹对于主裂纹的屏蔽和增强作用。Soh A K等[7]研究了多条微裂纹对主裂纹的影响。高山等[8]研究了界面主裂纹和微裂纹间的干涉。陈小翠等研究了基于扩展有限元方法的主次裂纹之间的影响[9]。王庆丰等[10]研究了不同位置裂纹间的相互作用。卿海等[11]研究了多条表面裂纹相互作用的应力。徐华等[12]利用有限元法直接求解了裂纹群裂尖应力强度因子。高健等[13]研究了一维正方准晶中半无限裂纹问题的解析解。 Chudnovsky A等[14]研究了微裂纹对主裂纹的影响。这些研究不同程度上都揭示了裂纹产生的原因，但由于真实的钢轨裂纹是在钢轨次表面上出现的，所以这些研究不能很好地解释钢轨次表面裂纹之间的影响。

本文利用弹性力学半平面体上的应力公式和Kachanov方法的核心思想，研究钢轨次表面裂纹之间的相互影响。采用简化的钢轨模型，以钢轨上的裂纹作为研究对象，计算了次表面上裂纹之间的影响，得到了裂纹尖端应力强度因子的解析解。

1 理论研究

1.1 研究模型

由于中国铁路技术的飞速进步，铁路运输向着高速、重载和高密度方向发展，这就导致钢轨的接触疲劳损伤越来越严重。钢轨表面、次表面的裂纹对钢轨的剥落掉块会有很大的影响。研究钢轨的次表面裂纹对于保护钢轨有很重要的意义。图1是钢轨实物[15],左图是裂纹向左上扩展，右图是裂纹向右扩展,椭圆圈标出的是裂纹有分叉的位置。

图1 含裂纹钢轨实物

从图1中的裂纹尺寸可见：钢轨上的裂纹相对于钢轨尺寸(钢轨高176 mm)是很小的，因此本文将钢轨处理为半无限大体，且在距离半无限大体表面很近的位置有裂纹，以模拟钢轨在次表面出现裂纹的情况，并通过施加局部荷载研究裂纹间相互影响作用。

1.2 问题求解

图2是平面应力状态的理论分析模型，所示在半无限大体中在边界ab上作用有分布力，它在各个点的集度为q=1 N/mm，在ab上距离坐标原点ξ处，取微小长度dξ。将dF=qdξ看作一个微小的集中力，因此可以得出dF=qdξ在M点引起的应力。

(1)

(2)

(3)

由式(1)～(3)可以得出：

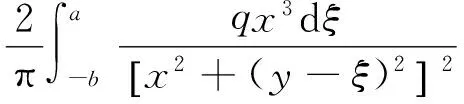
(4)

(5)

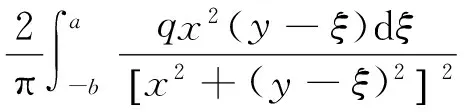
(6)

根据式(4)～(6)可以求出裂纹上的应力，然后采用Kachanov简化方法[5-6]计算裂纹尖端的应力强度因子：

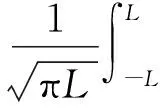
(7)

图2 理论示意图

2条裂纹情况：2条裂纹长度为2L，距离为h，用KⅠ/KⅠ0表示裂纹间相互作用影响。KⅠ表示2条裂纹相互影响时A裂纹的应力强度因子，KⅠ0表示在半无限大体与表面距离较大时单独一条裂纹时的应力强度因子。此时

(8)

p∞可以用σx在裂纹面上积分求出，

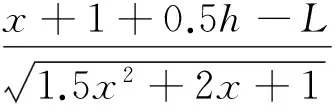
(9)

(10)

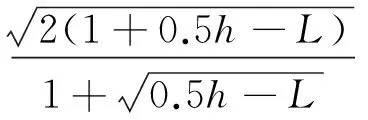
(11)

(12)

令图3中a=1 mm,b=1 mm,L=0.4 mm,可以计算2条共线裂纹相互影响的结果。

图3 2条裂纹的布置图

3条裂纹情况：每条裂纹长度为2L，距离为h，用KⅠ/KⅠ0表示裂纹间相互作用影响。KⅠ表示3条裂纹相互影响时B裂纹的应力强度因子，KⅠ0表示在半无限大体与表面距离较大时单独一条裂纹时的应力强度因子。此时：

(13)

p∞可以用σx在裂纹面上积分求出，

(14)

(15)

(16)

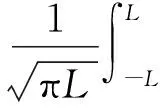
(17)

令a=1 mm,b=1 mm,可以计算3条共线裂纹相互影响的结果。

图4 3条裂纹的布置图

2 计算结果与讨论

2.1 有限元模型

2.1.1 有限元模型的建立

为了验证第1部分的理论推导，建立了一个二维的有限元模型。模型的长度为40 mm，宽度为40 mm，裂纹长度为0.8 mm。材料的弹性模量为210 GPa，材料的泊松比为0.3，因此可以当作一个半无限大体。单元类型是plane183。裂纹尖端用奇异三角形单元。在模型局部-1到1的表面施加q=1 N/mm的均布荷载。裂纹区域网格见图5。

图5 裂纹区域网格

2.1.2 结果修正

在理论计算时采取了半无限的模型，考虑无限域处理带来的理论误差，可以基于有限元的结果对模型做适当的修正(图6)。通过对数据的对比分析发现，随着裂纹深度的不同误差不同，所以采用了修正函数修正误差。

(18)

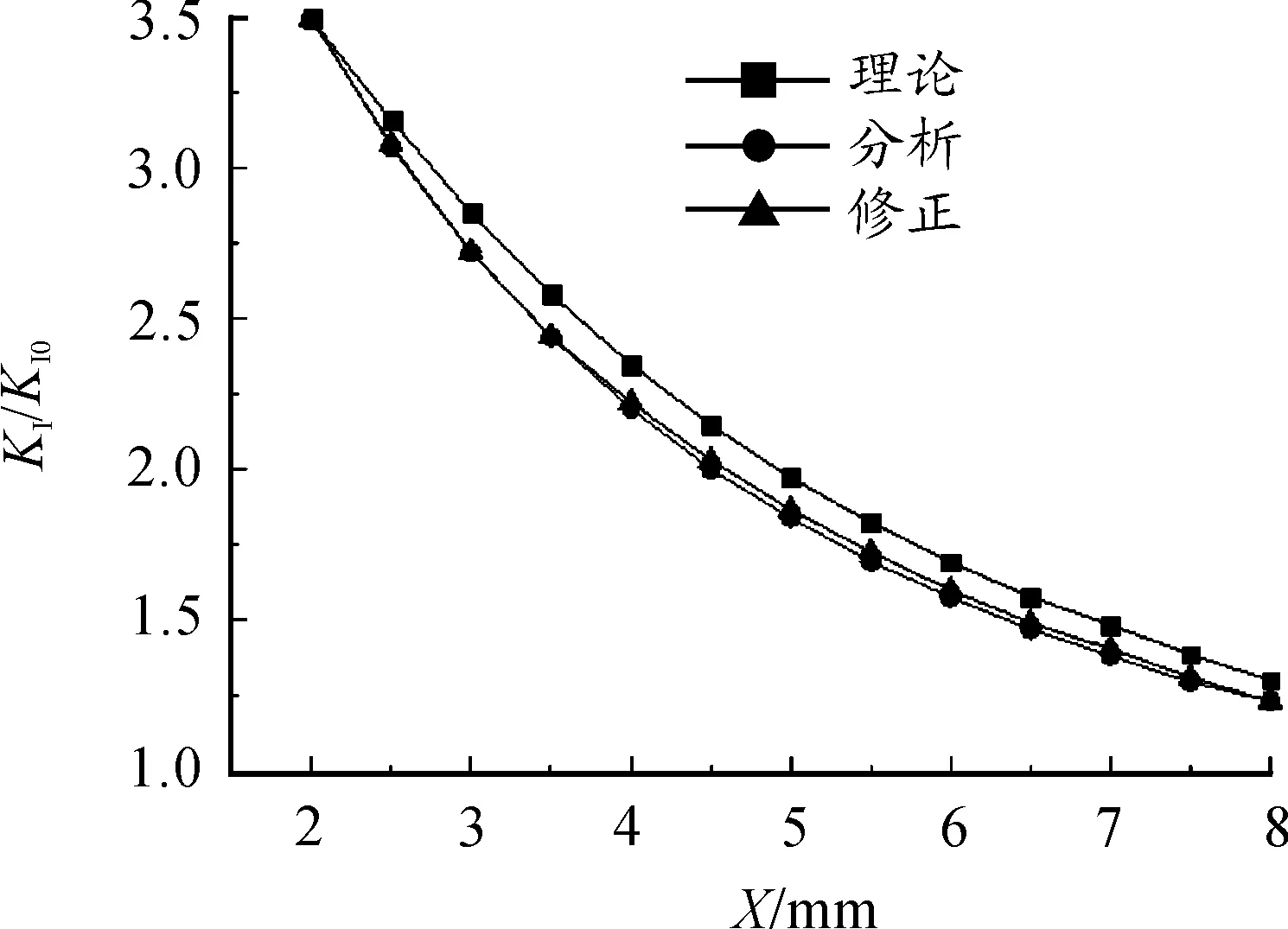
图6 误差修正

2.2 2条共线裂纹间的相互影响

这一部分将分析半无限大体中，在局部载荷作用下，2条平行于表面的共线裂纹之间的相互影响。

图7给出了裂纹尖端应力强度因子随着与表面距离变化的结果。模型的参数选取为：a=1 mm,b=-1 mm,L=0.4 mm。从图7可以看出：随着与表面距离的增大，裂纹尖端应力强度因子越来越小，这是因为与表面距离越大，表面对裂纹的影响就越小。还可以看出：在与表面距离保持一定时，裂纹之间的距离越大，裂纹尖端的应力强度因子越大，这是因为裂纹之间的距离越大，裂纹之间的影响就越小。

图7 KⅠ/KⅠ0随着x的变化曲线

图8给出了裂纹尖端应力强度因子随着裂纹之间的距离变化的结果。模型的参数选取为：a=1 mm,b=1 mm,L=0.4 mm。从图8可以看出：随着裂纹之间距离的增大，裂纹尖端应力强度因子越来越小，这是因为裂纹之间距离越大，裂纹之间的相互影响就越小。还可以看出：在裂纹间的距离保持一定时，裂纹与表面距离越大，裂纹尖端的应力强度因子越小，这是因为与表面距离越大，表面对裂纹的影响就越小。这种趋势与图7的趋势是一样的。

2.3 3条共线裂纹间的影响

这一部分将分析半无限大体中，在局部载荷作用下，3条平行于表面的共线裂纹之间的相互影响。

图9给出的是在局部荷载作用下半无限大体中3条共线裂纹尖端应力强度因子随着裂纹间距离变化的结果。模型的参数选取为:a=1 mm,b=1 mm,L=0.4 mm。从图9可以看出：随着裂纹间距离的增大，裂纹尖端应力强度因子越来越小，这是因为裂纹之间距离越大，裂纹之间的相互影响就越小。还可以看出：在裂纹间的距离保持一定时，裂纹与表面距离越大，裂纹尖端的应力强度因子越小，这是因为与表面距离越大，表面对裂纹的影响就越小。这种趋势与两条裂纹时的趋势是一样的。

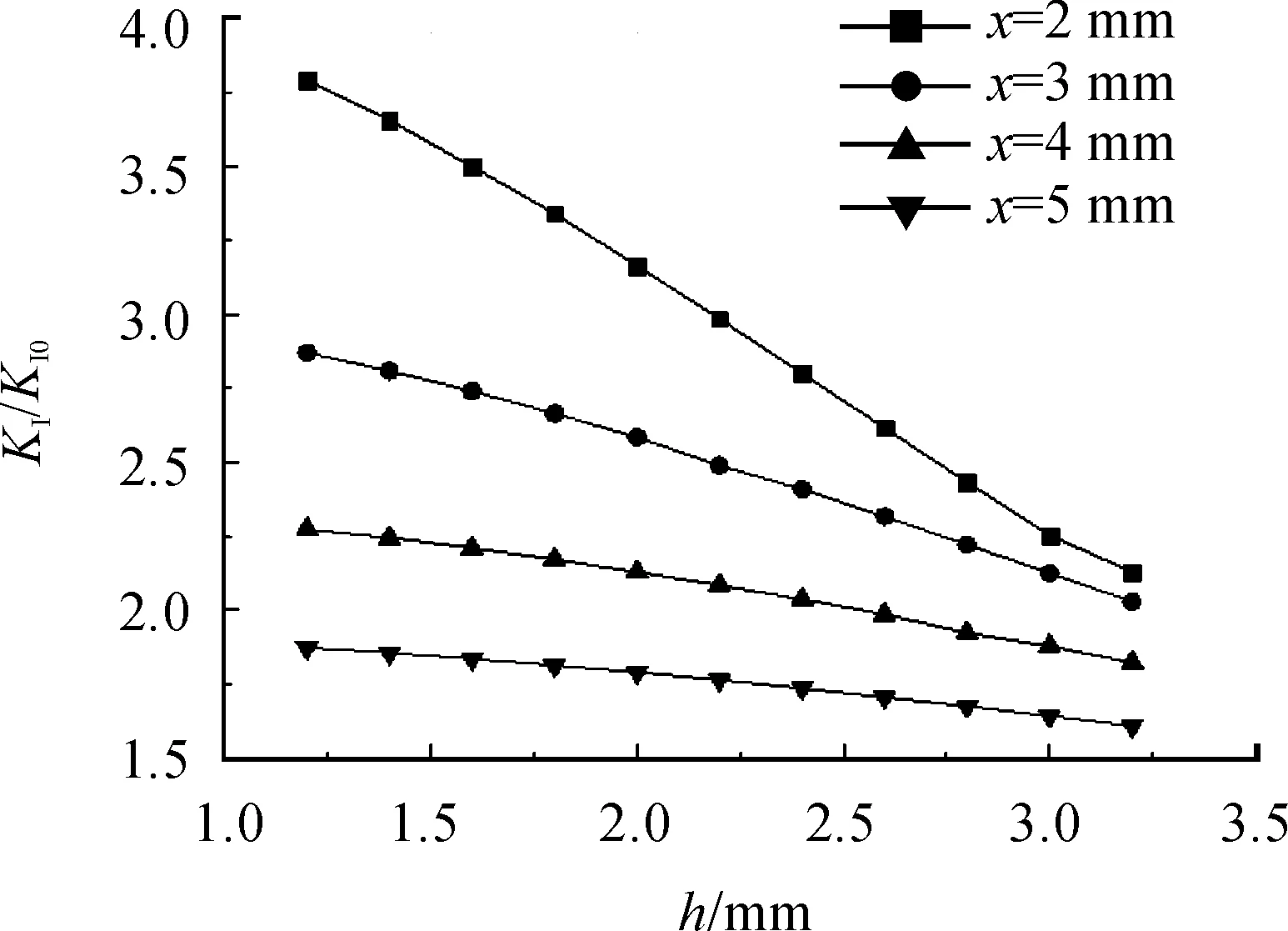
图8 KⅠ/KⅠ0随着h的变化曲线

图9 随着h变化的KⅠ/KⅠ0的曲线

图10给出的是在局部荷载作用下半无限大体中3条共线平行裂纹随着L变化的裂纹尖端应力强度因子结果。模型的参数选取为：a=1 mm,b=1 mm,L=0.4 mm,h=2 mm。从图10可以看出：随着裂纹长度的增大，裂纹尖端应力强度因子越来越大，这是因为裂纹长度越大，裂纹面上的应力就越大，并且裂纹尖端会越接近。同时能够看出，在裂纹长度保持一定时，裂纹之间的距离越大，裂纹尖端的应力强度因子越小。

无论是3条共线裂纹还是2条共线裂纹，裂纹的应力强度因子之所以会随着裂纹长度、距离改变而变化，本质上是裂纹上的应力场受到其他裂纹的影响而发生变化。因此，研究这些影响有利于对裂纹的扩展做出理论上的解释，进而解决工程上的问题。

图10 随着L变化的KⅠ/KⅠ0的曲线

3 结论

1) 裂纹与表面的距离对于裂纹之间影响很大，距离表面越近的裂纹彼此间影响会越大，容易造成裂纹在钢轨中扩展，使钢轨表面产生微小剥离，所以应该定期检查钢轨损坏情况。对于距离表面比较近的次表面裂纹，应该采取预防性打磨的形式消除剥离的隐患。

2) 裂纹长度会对裂纹间的影响产生较大作用，对于长度比较大的次表面裂纹区域应重点监测检查，这种长度的裂纹更加容易扩展，会对钢轨造成破坏，可以采用维修性打磨的形式防止危害。

3) 裂纹之间的距离对裂纹间的相互影响会有显著作用，对于次表面裂纹密集的区域，因为裂纹之间距离很近，这些区域的裂纹极易相互影响扩展形成较长的裂纹，对钢轨造成比较严重的破坏，故应根据实际情况采取维修性打磨形式或替换的措施保护钢轨正常使用。

钢轨的破坏会影响列车的行车安全，而钢轨的主要破坏形式是钢轨踏面的剥离掉块，因此，消除钢轨次表面微裂纹的影响带来的剥离可以有效地延长钢轨使用寿命，提高钢轨使用效率。

[1] 郭火明,王文健,刘腾飞,等.重载铁路钢轨损伤行为分析[J].中国机械工程,2014,25(2):267-272.

[2] 闫相桥.主裂纹与微裂纹相互作用的有效算法[J].力学学报,2006,38(1):119-124.

[3] 夏晓舟,章青,乔丕忠,等.裂纹间作用机制探讨及微裂纹区对主裂纹的作用效应研究[J].应用数学和力学,2010,31(1):61-70.

[4] 王恒,柳占立,许丹丹，等.微裂纹群与主裂纹相互作用的扩展有限元分析[C]//北京力学会学术年会论文集.北京：北京力学会，2015.

[5] KACHANOV M.Elastic solids with many cracks:A simple method of analysis[J].International Journal of Solids & Structures,1987,23(1):23-43.

[6] KACHANOV M.A simple technique of stress analysis in elastic solids with many cracks[J].International Journal of Fracture,1985,28(1):R11-R19.

[7] SOH A K,YANG C H.Numerical modeling of interactions between a macro-crack and a cluster of micro-defects[J].Engineering Fracture Mechanics,2004,71(2):193-217.

[8] 高山,王晓明.界面主裂纹和微裂纹之间的干涉[J].力学学报,1997,29(3):287-295.

[9] 陈小翠,杜成斌,江守燕.基于XFEM的主次裂纹间应力强度因子相互作用[J].河海大学学报(自然科学版),2014,42(4):327-331.

[10] 王庆丰,黄小平,崔维成.不同位置裂纹间的互相作用及其影响规律的有限元分析[J].江苏科技大学学报(自然科学版),2006,20(1):16-19.

[11] 卿海,杨卫,吕坚.多条表面裂纹相互作用的应力分析[J].工程力学,2009,26(1):1-6.

[12] 徐华，徐德峰，杨绿峰.裂纹群应力强度因子分析的广义参数有限元法[J].应用数学和力学，2016，37(10)：1039-1049.

[13] 高健，刘官厅.一维正方准晶中半无限裂纹问题的解析解[J].应用数学和力学，2015,36(9):945-955.

[14] CHUDNOVSKY A,DOLGOPOLSKY A,KACHANOV M.Elastic interaction of a crack with microcracks[J].Fracture,1984(4):825-832.

[15] 周剑华，任安超，吉玉，等.U71Mn 钢轨踏面剥离掉块缺陷分析[J].中国铁道科学，2013，34(2)：1-6.

(责任编辑刘 舸)

InteractionAmongSubsurfaceCracksinanElasticHalf-Plane

ZHANG Yanku, YANG Hongda, ZAN Xiaodong, XING Shuaibing, JIANG Xiaoyu

(School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)

It is simplified as a half-plane contains micro-cracks for the problem of micro-cracks on the subsurface of the rail. It analyzed the interaction between the micro-cracks in the half-plane. The tractions along the cracks are obtained from the stress formula of a half-plane subjected to a normal distribution force at the boundary in the elastic mechanics. Based on Kachanov’s simplified method, the solution of a half-plane containing the micro-cracks is presented. The stress intensity factor at the crack tip is obtained and the interaction among collinear micro-cracks is analyzed. The results show that the interaction among cracks decreases with the distance among the cracks increasing, and the distance between the micro-crack and the surface increasing and the crack size decreasing.

stress intensity factor; semi-infinite; cracks

2017-06-28

国家自然科学基金资助项目(11472230)；国家自然科学基金重点资助项目(U1134202,E050303);四川省青年科技创新团队资助项目(2013TD0004)

张言库(1990—)，男，山东聊城人，硕士，主要从事应用力学研究，E-mail:1911778208@qq.com。

张言库， 杨鸿达， 昝晓东， 等.半无限大体中次表面裂纹间的相互影响[J].重庆理工大学学报(自然科学)，2017(10):90-95.

formatZHANG Yanku, YANG Hongda, ZAN Xiaodong, et al.Interaction Among Subsurface Cracks in an Elastic Half-Plane[J].Journal of Chongqing University of Technology(Natural Science)，2017(10):90-95.

10.3969/j.issn.1674-8425(z).2017.10.015

O346.1

A

1674-8425(2017)10-0090-06