应用空电联合制动的重载列车缓解性能
杨 敏,王开云,史智勇,閤 鑫,周义昌
(西南交通大学 牵引动力国家重点实验室, 成都 610031)
应用空电联合制动的重载列车缓解性能
杨 敏,王开云,史智勇,閤 鑫,周义昌
(西南交通大学 牵引动力国家重点实验室, 成都 610031)
基于列车纵向动力学理论,研究了空电联合制动模式下列车编组、坡道坡度、电阻制动系数及缓解速度对列车在长大下坡道调速制动时缓解性能的影响。与单独空气制动模式进行了对比,分析了2种制动模式下列车实施循环制动的次数与最大车钩力的差异。研究结果表明:电阻制动系数越高,列车缓解性能越优;列车缓解性能随列车编组数量、坡道坡度与缓解速度的增加而变差;空电联合制动时,列车实施循环制动的次数与最大车钩力均小于单独空气制动时。
列车纵向动力学;长大下坡道;空电联合制动;缓解时间;缓解性能
随着重载铁路运输的发展,列车轴重和编组长度不断增加,长编组大轴重货物列车在长大下坡道调速制动时的安全问题日益凸显[1-3]。例如,国内某重载机车在长大下坡道制动时出现车体横向错位等严重影响列车安全运营的现象[4]。诸如此类的问题越来越引起相关部门重视。有大量学者针对重载列车制动特性进行了深入研究。范佩鑫[5]分析了万吨列车在长大下坡道调速制动运行工况下的纵向冲动及其规律;魏伟等[6]研究了制动特性对重载列车纵向冲动的影响;池茂儒等[7]采用循环变量法分析了长大重载列车在直线轨道、曲线轨道和坡道上制动时的动力学性能。特别地,列车调速制动缓解环节的安全问题受到众多学者关注。魏伟等[8]研究了列车的编组长度及减压量对缓解波速的影响;王奇钟[9]对重载列车最低缓解速度值进行了计算。调速制动缓解时,列车制动方式主要包括空气制动和电阻制动。孙树磊等[10-11]建立了用于列车纵向冲动研究的空气制动模型;黄超[12]对列车采用空电联合制动通过长大下坡道区段的纵向动力学进行了计算;左建勇等[13]建立了地铁列车空气制动系统仿真模型,并进行了仿真分析;林晖等[14]对重载列车有线电控空气制动系统进行了研究。
到目前为止,对列车空气制动、电阻制动和列车缓解的研究已较为成熟,但采用空电联合制动对列车缓解性能的影响研究仍较少。
本文采用重载列车纵向动力学模型,研究空电联合制动模式下列车编组、坡道坡度、电阻制动系数及缓解速度对列车在长大下坡道调速制动时缓解性能的影响;与单独空气制动模式进行了对比,分析了2种制动模式下列车实施循环制动的次数与最大车钩力的差异,以期为重载列车在长大坡道的操作优化提供理论依据。
1 模型建立
1.1 列车纵向动力学模型
基于列车纵向动力学基本理论,考虑列车的牵引特性、制动特性、钩缓特性和各类运行阻力[15],建立重载列车在长大下坡道纵向运动模型,如图1所示。
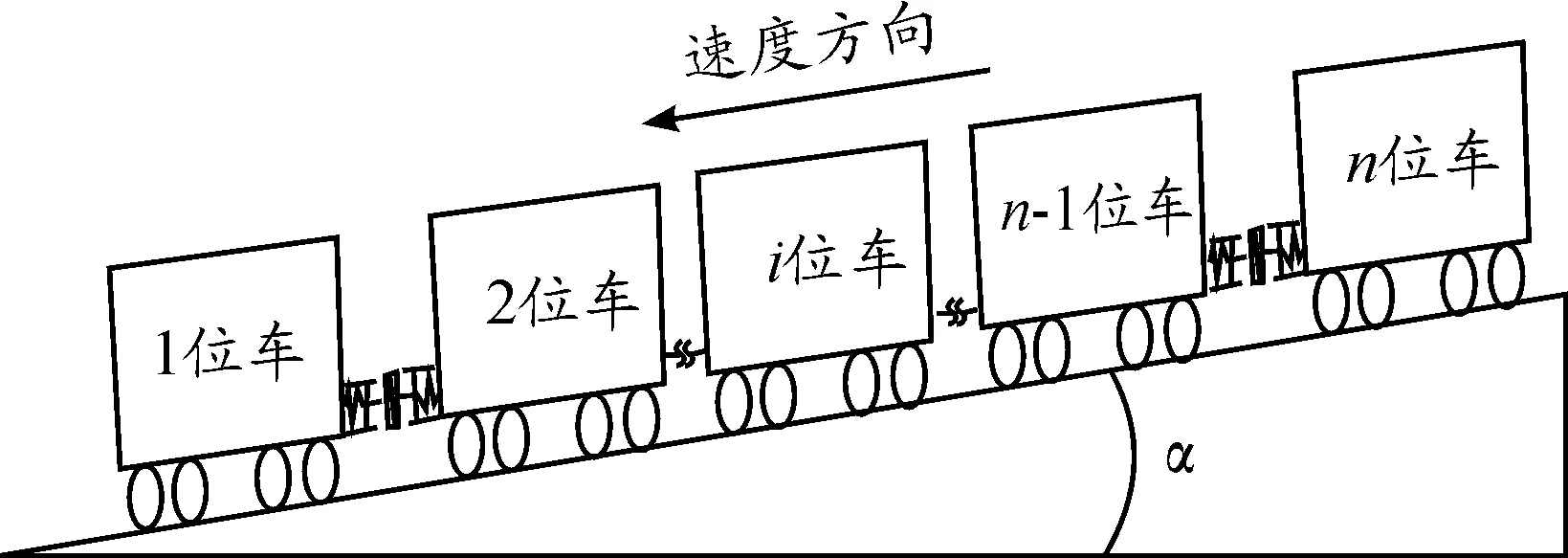
图1 列车在长大下坡道运动时纵向运动模型
将列车中每节机车车辆看作单独分离体,对n节机车车辆分别建立运动微分方程,可构建由n个微分方程组成的方程组。每节机车车辆受力分析如图2所示,其运动微分方程如下所示:
FDBi-FBi+FGi
(1)
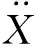
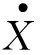
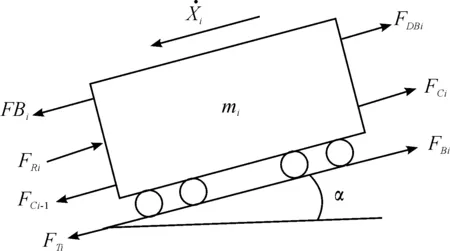
图2 第i位车的受力示意图
车钩力计算时,按图3给出的车钩缓冲器模型进行插值计算,车钩缓冲器在加载时按曲线fl(x)插值,卸载时按曲线fb(x)插值,具体计算公式为:
(2)
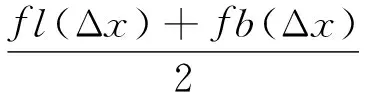
(3)
式中:Δx表示相邻两车的位移之差;Δv表示相邻两车的速度之差。

图3 车钩缓冲器系统模型
1.2 制动力模型
列车制动方式主要包括空气制动和电阻制动。列车电阻制动是指将原来的牵引电动机转变为发电机,从而达到制动效果的制动方式。图4给出了SS4B型电力机车的电阻制动特性曲线[17],t时刻列车的电阻制动力为:
(4)
式中:t0为机车开始实施电阻制动时刻;Δt为电阻制动力从零线性上升到最大值f(v)所需的时间;v为t时刻机车的运行速度;η为电阻制动的使用系数。
列车空气制动是指以压缩空气为原动力的制动方式,其具体特性表现为列车管压力和各制动缸压力随制动时间的变化,可根据试验及线路测试拟合得到。空电联合制动是指在列车实施空气制动、缓解的同时实施电阻制动。

图4 SS4B型电力机车电阻制动特性曲线
1.3 模型求解方法
所建列车纵向动力学微分方程组含有多个非线性因素,包含机车的牵引、制动特性和各类运行阻力等。
目前,非线性微分方程组的经典求解方法有隐式法和显式法。常用的隐式法有Newmark-β法、Wilson-θ法等,其特点是求解的稳定性较好、有益于时间积分步长的选取,但对于大型工程计算量较大。经典的显式法有中心差分法、四阶Runge-Kutta法。本文采用翟婉明院士提出的新型显式积分方法对此方程组进行数值积分求解[18],其特点是计算过程简捷、计算效率高,其数值积分格式为:
(5)
式中:Δt表示积分步长;角标n、n-1、n+1分别表示当前时刻t=nΔt、上一时刻t=(n-1)Δt、下一时刻t=(n+1)Δt;σ、φ表示控制积分方法特性的独立参数,起步运算时,两参数均设为0。
2 计算机模拟结果分析
为探明2种制动模式(空气制动、空电联合制动)下列车缓解性能差异,参考我国某实际重载铁路的万吨列车编组,设置列车编组为SS4B 型电力机车双机重联牵引KM70货车,列车缓解终止速度为55 km/h。
对于列车缓解性能的评价,从安全角度出发,列车缓解时间应不小于列车管再充气时间,其缓解时间越长,表明用于列车管再充气的时间越充足,即列车缓解性能越优。同时,列车在长大下坡道一次完整调速制动距离越长,即实施循环调速制动的次数越少,缓解时车钩力越小,表明其缓解性能越优。
2.1 编组及坡度对缓解性能的影响
为了研究列车编组数量与坡道坡度对列车缓解性能的影响,特设置2个工况,其参数列于表1。
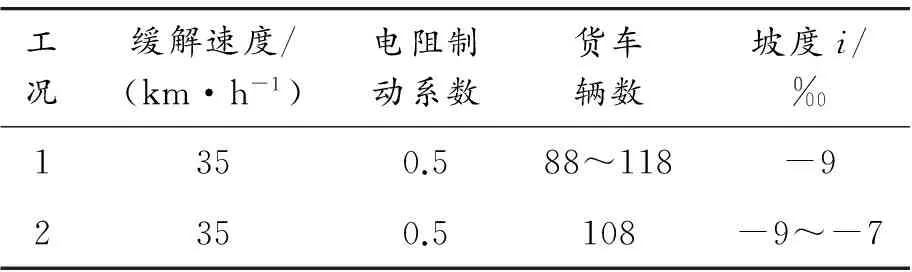
表1 列车编组及坡道坡度设置
图5给出了不同编组条件下,2种制动模式缓解过程所需的缓解时间。空电联合制动时,列车编组数量越多,所需缓解时间越少,单独空气制动时列车所需缓解时间几乎不变。由此可知:当空电联合制动时,列车编组数量越少,缓解性能越优。

图5 不同编组对列车缓解性能的影响
图6给出了不同坡道坡度条件下,2种制动模式缓解过程所需的缓解时间。列车所需缓解时间随坡道坡度的增加而降低,即坡道坡度越小,列车缓解性能越优。
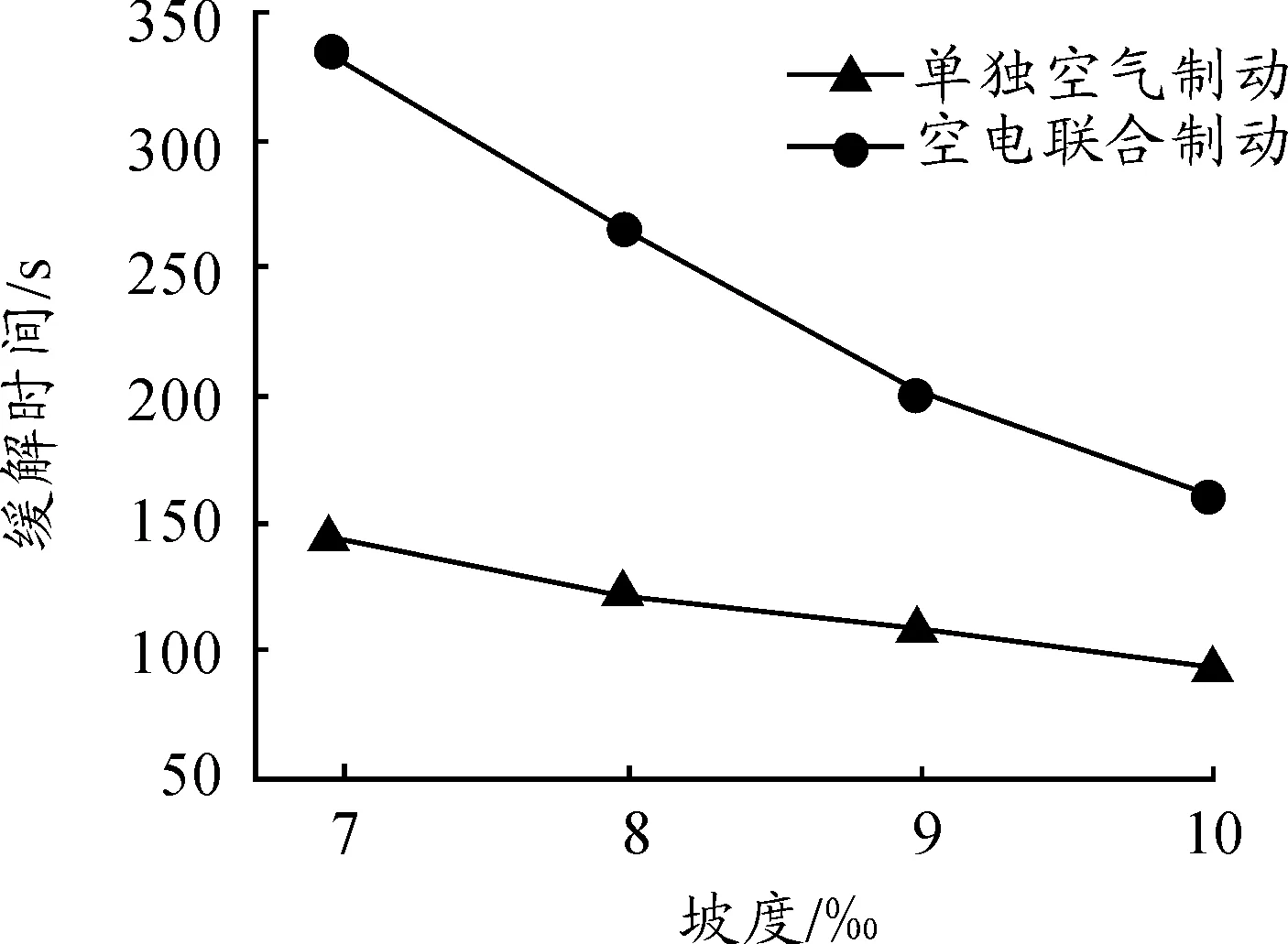
图6 不同坡道坡度对列车缓解性能的影响
2.2电阻制动系数及缓解速度对缓解性能的影响
在研究电阻制动系数对重载列车缓解性能的影响时,列车及线路参数为工况3。在研究缓解速度对重载列车缓解性能的影响时,列车及线路参数为工况4(表2)。
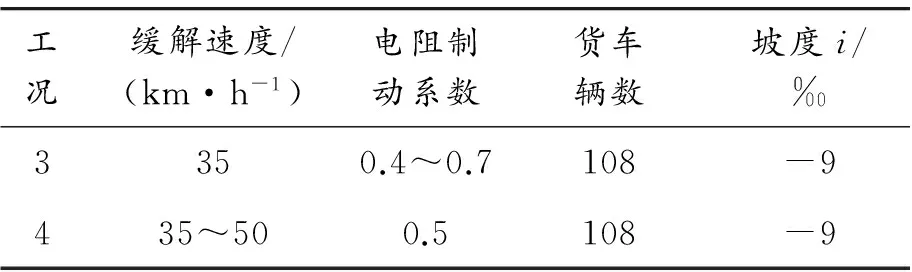
表2 列车电阻制动系数及缓解速度设置
图7给出了不同电阻制动系数条件下两种制动模式缓解过程所需的缓解时间。空电联合制动时,电阻制动系数越高,列车所需缓解时间越长;单独空气制动时,列车所需缓解时间不变。由此可知:空电联合制动时,列车电阻制动系数越高,缓解性能越优。
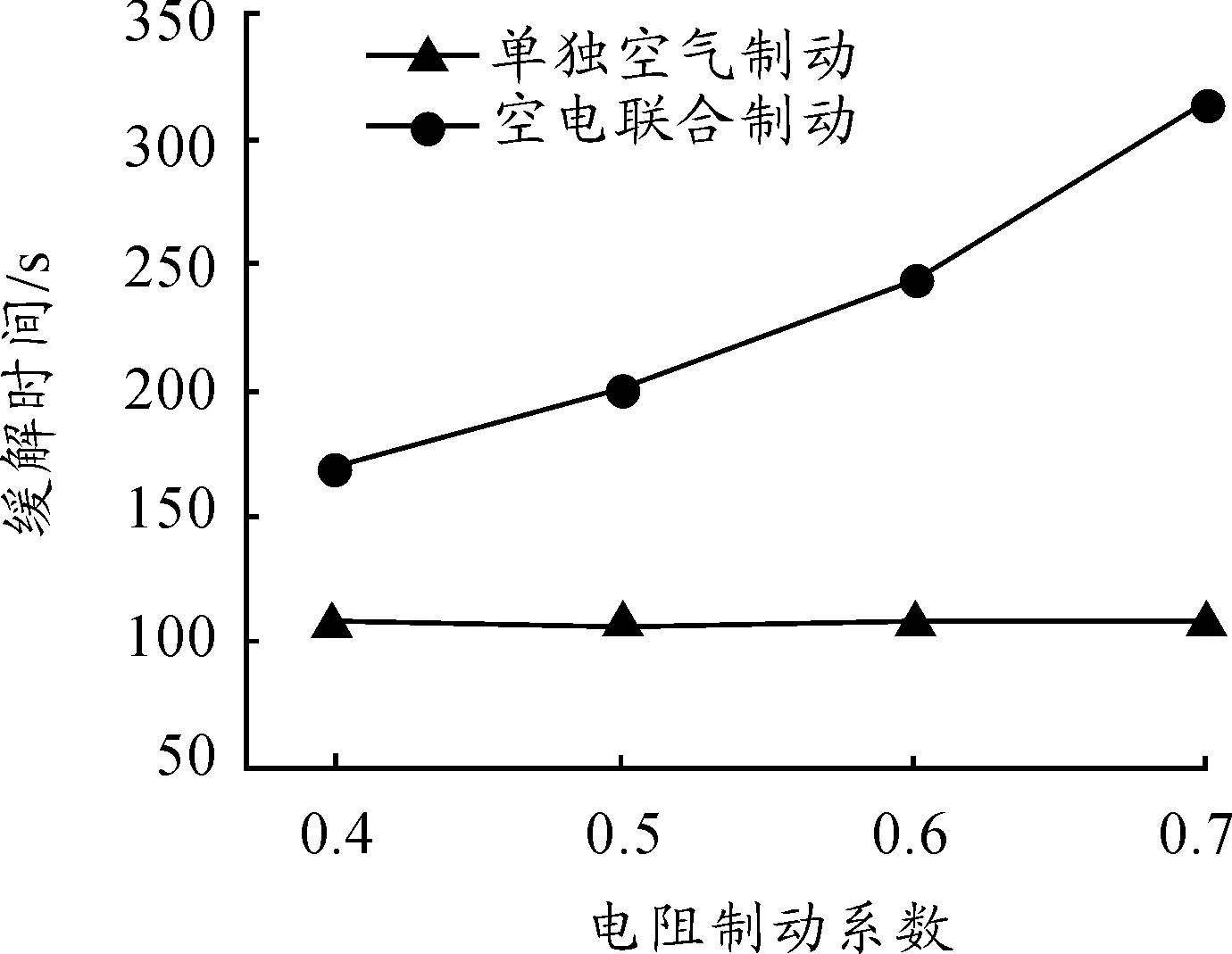
图7 不同电阻制动系数对列车缓解性能的影响
图8给出了不同缓解速度条件下2种制动模式缓解过程所需的缓解时间。列车所需缓解时间随缓解速度的增加而降低,即缓解速度越低,列车缓解性能越优。
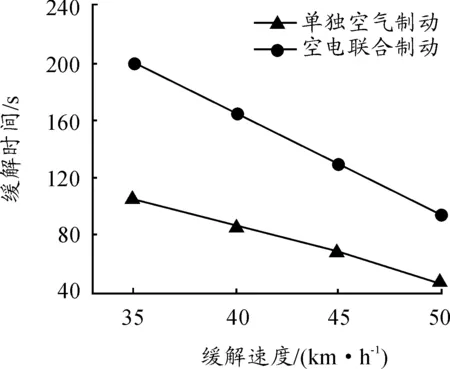
图8 不同缓解速度对列车缓解性能的影响
2.3 2种制动模式下循环制动次数与最大车钩力
为了研究2种制动模式下制动距离与最大车钩力的差异,表3给出了列车及线路的相关参数设置(工况5)。

表3 列车及线路参数设置
图9给出了2种调速制动模式下列车在一次完整调速制动过程中运行速度随制动距离的变化。与单独空气制动工况相比,采用空电联合制动后,列车的运行距离有所增加。单独空气制动时列车运行距离为2 707.7 m,空电联合制动时列车运行距离为3 224.6 m,增加了19.1%。由此可知:采用空电联合制动有利于减少列车在下坡道实施循环制动的次数。
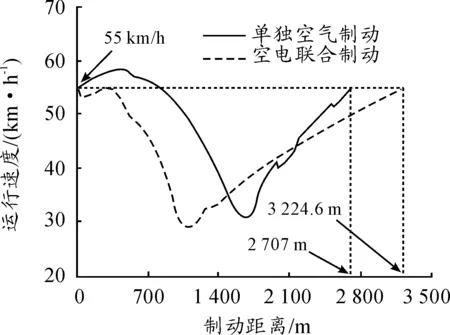
图9 不同制动模式时列车运行速度随制动距离的变化
表4给出了列车在2种制动模式缓解过程的最大车钩力。单独空气制动时列车最大车钩力为449.97 kN,空电联合制动时列车最大车钩力为386.85 kN,减少了14.0%。由此可知,采用空电联合制动能有效减小列车缓解过程的最大车钩力。

表4 不同制动模式时列车最大车钩力
综上,空电联合制动时列车缓解性能优于单独空气制动。
3 结论
本文研究了空电联合制动模式下列车编组、坡道坡度、电阻制动系数及缓解速度对列车缓解性能的影响。与单独空气制动模式进行了对比,分析了2种制动模式下列车实施循环制动的次数与最大车钩力的差异,结果表明:
1) 空电联合制动时,列车所需缓解时间随电阻制动系数的增加而增加,随列车编组数量、坡道坡度与缓解速度的增加而减小,即列车编组数量越少、坡道坡度越小、电阻制动系数越高、缓解速度越低,列车的缓解性能越优。
2) 空电联合制动时列车缓解性能优于单独空气制动。相对于单独空气制动模式,采用空电联合制动有利于减少列车在下坡道实施循环制动的次数,并能有效减小列车在缓解过程中的最大车钩力。
[1] LIU Pengfei,WANG Kaiyun.Effect of braking operation on wheel-rail dynamic interaction of wagons in sharp curve[J].Journal of Multi-body Dynamics,2017,231(1):252-265.
[2] ABOUBAKR A K,VOLPI M,SHABANA A A.Implementation of electronically controlled pneumatic brake formulation in longitudinal train dynamics algorithms[J].Proceedings of the Institution of Mechanical Engineers,Part K:Journal of Multi-Body Dynamics,2016,230(4):505-526.
[3] LIU Pengfei,ZHAI Wanming,WANG Kaiyun.Establishment and verification of three-dimensional dynamic model for heavy-haul train-track coupled system[J].Vehicle System Dynamics,2016,54(11):1511-1537.
[4] SHI Zhiyong,WANG Kaiyun,GUO Lirong,et al.Effect of arc surfaces friction coefficient on coupler stability in heavy haul locomotives:simulation and experiment[J].Vehicle System Dynamics,2017,55(9):1368-1383.
[5] 范佩鑫.重载列车牵引、调速及紧急制动的纵向力——大秦线万吨列车试验研究[J].西南交通大学学报,1994,29(1):57-64.
[6] 魏伟,于海龙.制动特性对重载列车纵向冲动影响的比较[J].大连交通大学学报,2013,34(4):1-6.
[7] 池茂儒,蒋益平,张卫华,等.长大重载列车系统动力学[J].交通运输工程学报,2011,11(3):34- 40.
[8] 魏伟,王自力,陈清.列车制动系统缓解性能的动态模拟[J].西南交通大学学报,1995,30(4):462- 465.
[9] 王奇钟.重载列车低速缓解速度值探讨[J].铁道机车车辆,2007,27(1):48-53.
[10] 孙树磊,李芾.重载列车纵向冲动动力学研究[J].中国铁道科学,2015,36(4):136-138.
[11] WEI Wei,HU Yang,WU Qing,et al.An air brake model for longitudinal train dynamics studies[J].Vehicle System Dynamics,2017,55(4):517-533.
[12] 黄超.托电铁路万吨重载列车纵向动力学性能分析[D].成都:西南交通大学,2015.
[13] 左建勇,王宗明,吴萌岭.地铁列车空气制动系统仿真模型[J].交通运输工程学报,2013,13(2):43- 47.
[14] 林晖,钱立新.重载列车有线电控空气制动系统的研究[J].中国铁道科学,2007,28(1):63-70.
[15] 严隽耄,翟婉明,陈清,等.重载列车系统动力学[M].北京:中国铁道出版社,2003.
[16] TB/T 1407—1998,列车牵引计算规程[S].
[17] 周光海,叶彪.SS4B型电力机车(4)——电器线路[J].机车电传动,1996(6):17-20.
[18] ZHAI Wanming.Two simple fast integration methods for large-scale dynamic problem in engineering[J].International Journal for Numerical Methods in Engineering,1996,39(24):4199- 4214.
(责任编辑林 芳)
ReleasePerformanceofHeavy-HualTrainBasedonElectric-PneumaticBlendBraking
YANG Min, WANG Kaiyun, SHI Zhiyong, GE Xin, ZHOU Yichang
(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)
Based on the theory of train longitudinal dynamics, the influence of train marshalling, slope gradient, resistance braking coefficient and release speed on release performance was analyzed under the mode of electric-pneumatic blend braking, during the speed adjustment braking of train on long down slope. A comparison was made between electric-pneumatic blend braking model and air braking model. The difference of numbers of cycle braking and maximum coupler force of train was illustrated under the two modes. Results indicate that the higher the resistance braking coefficient, the better the release performance is. The release performance declines with the increases of train marshalling, slope gradient and release speed.The numbers of cycle braking and maximum coupler force of the electric-pneumatic blend braking are less than air braking.
longitudinal dynamics;long downhill sections;electric-pneumatic blend braking; release time;release perform
2017-07-24
国家自然科学基金资助项目(51478399)
杨敏(1991—),男,四川广元人,硕士研究生,主要从事重载列车纵向动力学研究,E-mail: swjtuer1896@163.com; 通讯作者 王开云(1974—),男,江西萍乡人,博士,研究员,博士生导师,主要从事机车车辆-轨道耦合动力学研究,E-mail: kywang@swjtu.edu.cn。
杨敏,王开云,史智勇,等.应用空电联合制动的重载列车缓解性能[J].重庆理工大学学报(自然科学),2017(10):84-89.
formatYANG Min,WANG Kaiyun,SHI Zhiyong,et al.Release Performance of Heavy-Hual Train Based on Electric-Pneumatic Blend Braking[J].Journal of Chongqing University of Technology(Natural Science),2017(10):84-89.
10.3969/j.issn.1674-8425(z).2017.10.014
U260.35
A
1674-8425(2017)10-0084-06

