负熵最大化条件下的语音信号盲源分离技术研究

闫 姝，徐 岩

(1.兰州石化职业技术学院电子电气工程学院,甘肃 兰州 730060；2.兰州交通大学电子与信息工程学院，甘肃 兰州 730070)

负熵最大化条件下的语音信号盲源分离技术研究

闫 姝1，徐 岩2

(1.兰州石化职业技术学院电子电气工程学院,甘肃 兰州730060；2.兰州交通大学电子与信息工程学院，甘肃 兰州730070)

语音信号盲源分离是在不知道源信号和传输信道任何先验知识的情况下，仅根据输入语音源信号的统计特性，通过观察信号恢复出各个独立源信号的过程。基于负熵的FastICA算法的最大优点在于其收敛速度较快，是一种性能较好的学习算法，在语音信号盲源分离应用中具有较高的实用价值，但该算法存在计算量大的缺点。针对这一问题，提出了以负熵最大化作为目标函数，采用牛顿迭代法求解FastICA算法的方法。但由于牛顿迭代法求解非线性方程计算量较大，需改进雅克比矩阵算式，并使用相关系数来观察分离效果的优劣。仿真分析结果证明，改进后的算法由于未增加雅克比矩阵运算次数，所以收敛的迭代次数大幅度减少，使程序运行时间显著减小。该算法在兼顾算法收敛速度的同时，提高了算法的性能，较好地恢复了源语音信号。

负熵最大化； 牛顿迭代； FastICA； 雅可比矩阵； 混合矩阵； 分离矩阵； 盲源分离； 语音增强

0 引言

盲源分离(blindsoruceseparation,BSS)是指除了假设源信号统计独立外，仅由观测信号得到原始信号的过程[1]。独立分量分析(independentcomponentanalysis,ICA)算法是较为有效的资源分离处理方法[2]。ICA算法利用源信号的独立性和非高斯性，通常可以划分为两大类：基于信息论准则的迭代估计法和基于统计学的代数方法。

FastICA作为经典的ICA算法之一，由芬兰赫尔辛基工业大学的Hyvarien等在1997年提出。作为一种快速寻优迭代算法，FastICA在每一步迭代中需有大量的样本数据参与运算。基于负熵的FastICA算法采用基于负熵最大化判据的方法，依托非高斯性最大化原理，通过负熵最大化目标函数，使用固定点迭代理论寻找wTX的非高斯性最大值，实现对分离信号的最佳估计。

1 基于负熵最大化的FastICA算法

1.1盲源分离问题

盲源分离问题的研究对象，是由n维相互独立的信号源S(t)混迭形成的m维观测信号X(t)所产生的。盲源分离系统原理图[3]如图1所示。

图1 盲源分离系统原理图

根据图1，对盲源分离系统建立混合数学模型[4]：

X(t)=AS(t)+n(t)

(1)

式中：S(t)为n维未知源信号矢量;S(t)=[s1(t),s2(t),…,sn(t)]T，si(t)(i=1,2,…,n)为n个相互独立的随机信号；A为未知混合矩阵，A=(aij),j=1,2,…,m；X(t)为m维观测信号矢量X(t)=[x1(t),x2(t),…,xm(t)]T，每个观测信号xi(t)都是d个未知信号s(t)的线性组合；n(t)为m维加性观测噪声，n(t)=[n1(t),n2(t),…,nm(t)]T。

估计矢量Y(t)如式(2)所示。

Y(t)=WX(t)

(2)

若不考虑加性噪声影响，式(2)可简化为：

Y(t)=WX(t)=WAS(t)=PS(t)

(3)

式中：向量Y(t)和S(t)的近似程度用矩阵P来表示。P是一个n×n的矩阵，称为系统矩阵。盲源分离的问题就是估计W，即在源信号S(t)和混合矩阵A未知的情况下，求一个m×n的分离矩阵W(反混合矩阵)[5]。

ICA的发展与BSS紧密相连。在源信号相互统计独立的假设前提下，可以认为ICA与BSS的提法是完全一致的[6]。ICA算法目的就是找到混合信号的一个分离矩阵，其实质是线性变换矩阵，使输出尽可能地独立，即Y(t)=PS(t)。向量Y(t)是源信号S(t)的估计，若S(t)=Y(t)，即达到了恢复信号的目的。实际上，当矩阵P的各行各列只有一个元素接近1，其他元素接近0，就可以认为分离成功。

1.2FastICA算法

负熵最大化也称为信息传输最大化，是较为重要的非高斯性度量方法，在SNR较高的条件下，输入/输出之间信息量越大，它们之间的冗余量就越小。想要使输出的分量相互统计独立，则要使负熵最大化，即对应的互信息量最小。

假设输入X(t)=[x1(t),x2(t),…,xm(t)]T的概率密度函数为p1，高斯概率密度函数为pg，且p1、pg有相同的均值和方差。通过KL散度给出负熵定义[7]，如式(4)所示。

(4)

由式(4)可以得到p1(x)与高斯分布的相似程度。负熵的值是一个正数，或者当x为高斯分布时其值为0。由于负熵需要计算变量的概率密度函数，为了简化，常采用近似计算。

基于上述理论可以得知，系统输出负熵的最大化可以导致信号的分离，负熵的取值为非负性，当且仅当信号都是高斯分布时负熵的值为0，而且对y的任意线性变不受影响。所以负熵是一个很好的目标函数，可以用来描述一个分布与高斯分布的差异程度。式(5)为负熵和互信息两者之间的关系[8]。

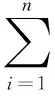
(5)

式中：Ji(yi)为yi的负熵；C为y的协方差矩阵；Cii为矩阵C的对角元素。

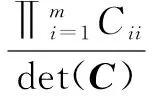
(6)

(7)

FastICA算法是独立分量分析中常用的一种快速算法。该算法的实质是一种快速寻优迭代算法，在每一步迭代中有大量的样本数据参与运算。负熵最大化作为FastICA算法的目标函数，得到的优化函数如式(8)所示[9]。

(8)

式中：ki为一个正常数；v为一个高斯随机变量，并且v的均值和单位方差为0。

假设y具有和随机变量v相同的形式，Gi(x)是一个非二次函数。当p=1时，负熵可以近似表示为式(9)。

J(y)∝{E[G(y)]-E[G(v)]}2

(9)

由式(2)可得：y=wTX。其中:X为接收到的混合矩阵；y为一个独立成分；w为分离矩阵W的任意一行。可将负熵的近似函数表述为式(10)[10]。

JG(W)∝{E[G(wTX)]-E[G(v)]}2

(10)

此时该问题就是求解分离矩阵W，可转化为求解信号y=wTX，使得JG(W)达到最大值。又因为E[wTx)2]=1，所以目标函数可写为：

(11)

在Kuhn-Tucker条件下，该问题转化为无限制的优化问题，进而得到目标函数：

F(w)=E[G(wTX)]+c(‖w‖2-1)

(12)

式中：c为常数。

用牛顿法求解该目标函数的最优解，可得快速ICA算法的迭代公式：

(13)

2 基于牛顿迭代法的改进算法

在利用牛顿迭代法求解非线性方程过程中，为了减少求雅克比矩阵的次数，对牛顿迭代法进行改进，即迭代过程的雅克比矩阵均为J(w0)，得到迭代公式：

(14)

该改进方法虽然能减少计算量，但却降低了迭代的收敛速度，有可能导致算法最后不能收敛，所以这种方法并不理想。本文提出的改进算法从减少计算量的角度出发，由于未增加雅克比矩阵次数，所以大幅度减少了收敛的迭代次数。假设wk已知，则wk+1为：

(15)

式中：收敛阶为m+1，且m每次迭代只需要计算1次J(w)。因此，该方法减少了计算量，提高了迭代速度。当m=2时，式(15)可以简化为式(16)。

(16)

将F(wk)和J(wk)所表示的内容代入式(16)，就是改进的FastICA在m=2时算法的迭代过程。

改进后的FastICA迭代算法步骤如下。

①选择初始随机权值矢量w0。

②用式(16)更新wk+1。

③归一化wk+1。

(17)

④如果|wk+1-wk|>ε，说明算法不收敛，返回步骤②;否则，计算出一个独立成分，算法结束。

由于在算法中每次只提取一个独立成分，在进行算法分离过程中，为避免重复抽取，每次提取后必须从观测信号中删减该独立成分。如此循环，直到所有的独立成分全部抽取出来。抽取计算式为：

(18)

3 算法仿真

仿真采用MatlabR2011a作为仿真工具，源信号是自行录制的3个相互统计独立的声音信号。先验条件是假设源信号相互独立。为保证算法有效性，对已录的3个语音信号进行测试，得到其相关系数分别为rs1s2=0.0070、rs1s3=0.0015、rs2s3=0.0185。测试3个语音信号的相关系数值rxy<0.2，可近似认为其相互独立。

源信号仿真结果如图2所示。

图2 源信号仿真图

由系统随机产生混合矩阵A，考虑m=n，得：

(19)

尽管混合矩阵A是系统生成的，但是所研究对象是观测信号，所以对信号分离没有影响。不考虑加性噪声的影响，在接收端可以得到观测信号X(t)=AS(t)。观测信号仿真结果如图3所示。

图3 观测信号仿真图

通过计算求得分离矩阵，同时生成解混信号。

分离W1矩阵为：

(20)

改进前的解混信号仿真结果如图4所示。

在仿真测试中，分离信号的顺序与源信号的顺序不一致，这就表明恢复信号的排列顺序有不确定性。具体对应关系为语音信号S1对应解混信号1，语音信号S2对应解混信号3，语音信号S3对应解混信号2。对比图4和图2可知，经过基于负熵最大化的FastICA算法，可以大致恢复源信号。

保持混合矩阵A不变，即观测信号不变，应用基于牛顿迭代法的改进算法来实现语音信号的分离，得到改进后的解混信号仿真结果如图5所示。

对比图5和图2可知，采用改进后的算法，分离后的信号与源信号基本一致。经计算，FastICA算法程序所用时间为1.024s，改进后程序所用时间为0.5735s。改进后算法所用的时间明显少于未改进算法，这表明算法的速度得到提高，即算法更加收敛。

图4 解混信号仿真图(改进前)

图5 解混信号仿真图(改进后)

4 结束语

从仿真结果分析得知，基于牛顿迭代法的改进FastICA算法有效地实现了信号分离。从减少计算量的角度出发，改进后的算法，由于未增加雅克比矩阵次数，收敛的迭代次数大幅度减少，程序运行时间显著缩短，算法更加高效。

[1] 马建芬.语音信号盲分离与增强算法的研究[M].北京:电子工业出版社,2012.

[2] 徐岩,王春丽.语音信号增强及其应用[M].北京:科学出版社,2014.

[3] 余先川,胡丹.盲源分离理论与应用[M].北京:科学出版社,2011.

[4] 同晓荣.独立分量分析盲源分离研究[J].微型电脑应用，2017,33(1):39-41.

[5] 高建彬.盲源分离算法及相关理论研究[D].成都：电子科技大学，2012:1-25.

[6] 吴微，彭华，张帆.FSATICA和ROBUSTICA算法在盲源分离中的性能分析[J].计算机应用研究，2014,31(1):95-98.

[7] 李智明.基于改进FastICA算法的混合语音盲分离[D].上海:上海交通大学，2015:29-33.

[8] 白琳,陈豪.一种语言信号欠定盲分离的新方法[J].空间电子技术,2012(2):16-19.

[9] 陈豪,白琳,周治宇.盲源分离技术的发展及应用浅谈[J].空间电子技术,2013(1):1-6.

[10]张月.负熵最大化的FASTICA心电消噪研究[D].太原：太原理工大学，2012:32-33.

ResearchontheBlindSourceSeparationTechnologyofSpeechSignalsunderNegativeEntropyMaximization

YAN Shu1,XU Yan2

(1.School of Electronic and Electrical Engineering，Lanzhou Petrochemical College of Vocational Technology,Lanzhou730060,China;
2.School of Electronic and Information Engineering,Lanzhou JiaoTong University,Lanzhou730070,China)

Voice signal blind source separation is the recovery process of each independent source signal,by observing signals and only in accordance with the statistical characteristics of the input speech source signals,without any prior knowledge about the source signal and transmission channel.The negative entropy based FastICA algorithm is a learning algorithm with better performance,its biggest advantage is fast convergence,and it has a good practical value in the application of blind source separation of voice signals; but the disadvantage of the algorithm is large amount of calculation.To solve this problem,the negative entropy maximization is used as the objective function,and FastICA formula is solved by Newton iterative method.Because the process of Newton iterative method for solving nonlinear equations still has a large amount of calculation,the Jacobian matrix formula is studied and improved; the correlation coefficient is used to observe the effect of separation.The results of simulation analysis prove that the improved algorithm does not increase the operation times of Jacobian matrix,so the number of iterations of convergence is greatly reduced and the running time of programs significantly decreased.Besides convergence speed,the algorithm also improves the performance,it well recovers the source voice signal.

Negative entropy maximization; Newton iteration; FastICA; Jacobian matrix; Mixed matrix; Separation matrix; Blind source separation; Speech enhancement

TH841；TP301.6

10.16086/j.cnki.issn1000-0380.201710012

修改稿收到日期:2017-06-06

国家自然科学基金资助项目(61461024)

闫姝(1984—)，女，硕士，讲师，主要从事多媒体信息处理方向的研究。E-mail274143818@qq.com。