仓储粮堆内部自然对流和热湿传递的数学分析及验证

王远成 潘 钰 尉尧方 魏 雷 张忠杰 赵会义 石天玉 尹 君

(山东建筑大学热能工程学院1, 济南 250101)(国家粮食局科学研究院2, 北京 100037)

仓储粮堆内部自然对流和热湿传递的数学分析及验证

王远成1潘 钰1尉尧方1魏 雷2张忠杰2赵会义2石天玉2尹 君2

(山东建筑大学热能工程学院1, 济南 250101)(国家粮食局科学研究院2, 北京 100037)

本文基于仓储粮堆内部自然对流、热湿耦合传递的数学模型，采用数学分析的方法对模型中各个方程中的各项的物理意义和数量级大小进行了分析，探讨了仓储粮堆内部自然对流、热量传递和水分迁移过程的相互关系。提出了判断粮堆内部自然对流强弱的瑞利数及其影响因素，分析了仓型结构、粮种及仓外大气温度对粮堆内部自然对流、热量传递和水分迁移的影响，并通过数值模拟对数学分析结果进行了验证。 结果表明，数学分析方法是分析仓储粮堆内部自然对流、热量传递和水分迁移过程的一种有效途径，数学分析的结果可以为仓型设计、储粮生态系统的模拟、仓储技术管理提供借鉴。

数学分析 粮堆 自然对流 热量传递 水分迁移

温度和水分是影响粮食安全储存的主要因素，准确预测粮仓中粮食的温度和水分是至关重要的。由于储粮的温度由周围的天气条件决定，所以周围天气的变化会影响到储粮的温度。同时，在温度梯度的作用下，粮堆内部形成自然对流运动，它也会促进粮堆内部的水分迁移，从而导致仓储粮堆的水分发生了迁移和再分配。为了探究非人工干预条件下粮堆内部温度和水分变化的规律，首先就需要了解和掌握粮堆内部自然对流和热湿传递过程。

Converse等[1]采用试验和数值模拟相结合的方法，对圆筒仓内部温度和水分变换规律进行了研究。Yaciuk等[2]、Jiang等[3]建立了在粮堆内部以导热为主要热量传递的模型，忽略了自然对流的影响，并对仓储粮食内部的温度变化进行了模拟分析。该研究认为，粮食在储存过程中会发生自然对流，但对储粮的温度并没有太大的影响。Fuji Jian等[4]采用长期(15个月)现场观测的方法调查了位于加拿大北部的金属钢板仓内部的小麦温度和水分变化规律，调查发现仓内小麦温度变化的峰谷值较仓外气温变化的峰谷值推迟一个月，而且在温度梯度的作用下，在粮仓内产生了空气的自然对流，导致仓内粮食水分的迁移。

Beukema等[5]对矩形粮仓中的自然对流和传热过程进行了研究，结果表明，自然对流会影响粮堆内部的热量传递。自然对流作用会使传热率升高，最终使温度达到一个稳定状态；数学模型中不考虑自然对流项时，计算出的温度会比考虑自然对流时得到的温度值低11%。Nguyen[6]发展了一个二维的瞬态模型来描述由于粮堆内部的自然对流而引起的水分迁移过程，但忽视了扩散引起的水分迁移。Khankari等[7-8]对仓储粮堆内部由于温度梯度及自然对流引起的温度和水分变化规律进行了研究，且他们考虑了由温度梯度引起的自然对流对储粮中热湿迁移的影响。王远成等[9-11]采用计算流体动力学技术(CFD)对圆筒仓和房式仓内粮堆的微气流流动、温度和水分随仓外大气温度的改变而变化的规律进行了数值模拟研究，研究发现，在非人工干预情况下，尽管粮堆内部的自然对流流动微弱，但对粮堆内部的水分迁移产生影响，而且粮堆内部热量传递和水分迁移过程是相互耦合的。

本研究基于仓储粮堆内部自然对流、热湿耦合传递的数学模型，对仓储粮堆内部热湿耦合传递过程进行了数学分析，得到了描述仓储粮堆自然对流强度的无量纲参数—瑞利数，探究了瑞利数对仓储粮堆内部热量传递及水分迁移的影响；同时分析了仓型、粮种、仓外大气温度及呼吸作用对仓储粮堆内部自然对流、热量传递和水分迁移的影响，得到了粮仓内部小麦和玉米储藏过程中自然对流和热量传递及水分迁移的特征。

1 粮堆内部自然对流和热湿传递过程的数学分析及验证

1.1 仓储粮堆内部自然对流的瑞利数

对仓储粮堆内部自然对流、热湿耦合传递的数学模型[9-11]进行数学变换，并引入流函数ψ，可以推导出：

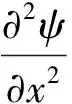
(1)

其中，H是粮仓中粮堆的高度，T是空气和多孔介质混合的绝对温度，A是粮仓周围空气温度变化幅度，α为粮堆热扩散系数。方程(1)中Ra是描述粮堆中自然对流强弱的无量纲数—瑞利数，其表达式如下：

Ra=KρagβAH/(μα)

(2)

它是描述粮堆内部自然对流强弱的一个准则数，它可以反映自然对流流动对对流换热强度的影响。对于一定仓型结构来说，Ra/H=KρagβA/μα。不难看出，瑞利数是反应粮堆内部的自然对流强弱的无量纲数，与渗透率K、仓外大气温度变化幅度A、粮堆热扩散系数α以及粮堆内部的空气的热物性参数有关。不同粮种的显著差异项是渗透率K和粮堆热扩散系数α。A和β受周围环境温度的影响，而渗透率主要与粮粒等效直径及孔隙率有关。

1.2 粮堆内部的自然对流流动

由于密闭粮仓内部压力变化很小，即∂p为100数量级，粮堆跨度∂x≈12，粮堆高度∂y≈6。而且，考虑粮堆内的小麦渗透率K=5.96×10-9m2和空气的运动黏度μ=1.79×10-5Pa·s，ρa=1.23 kg/m3，空气的体积膨胀系数β=0.003 4，仓外大气温度与粮堆平均温度之差T-Ta=15 ℃。对描述粮堆内部流动的达西方程[9-11]进行近似分析，可以得到：

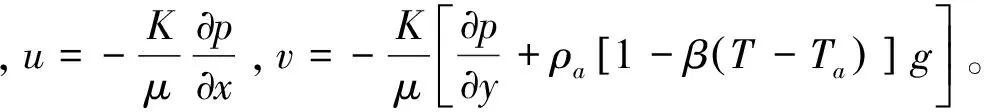
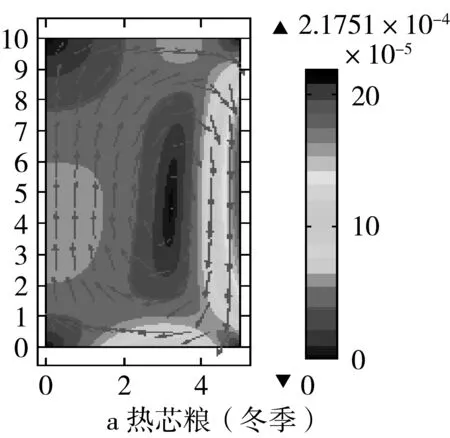
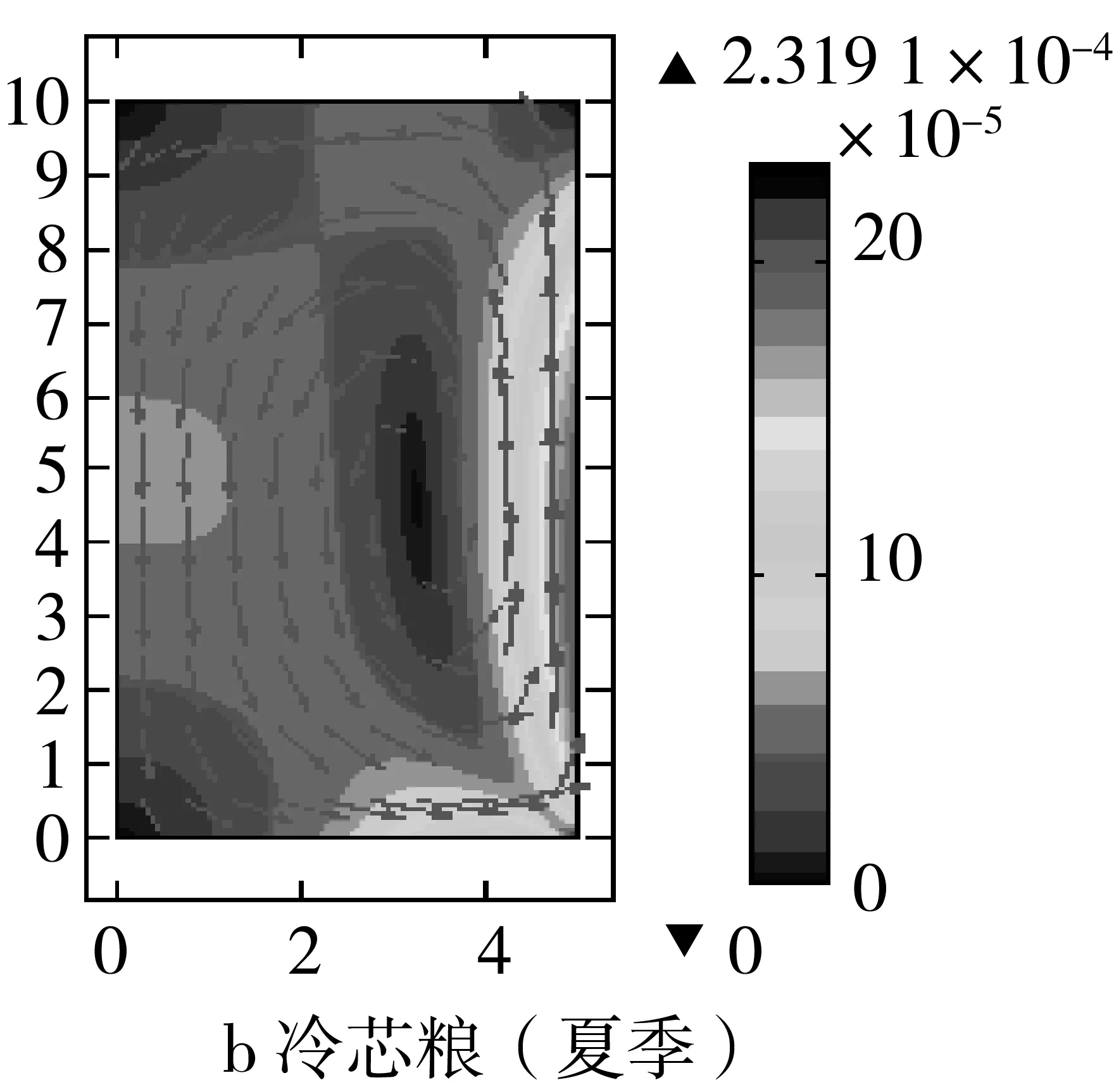
图1 王远成等模拟的近似冬季和夏季储藏150天时浅圆仓内小麦的流场分布

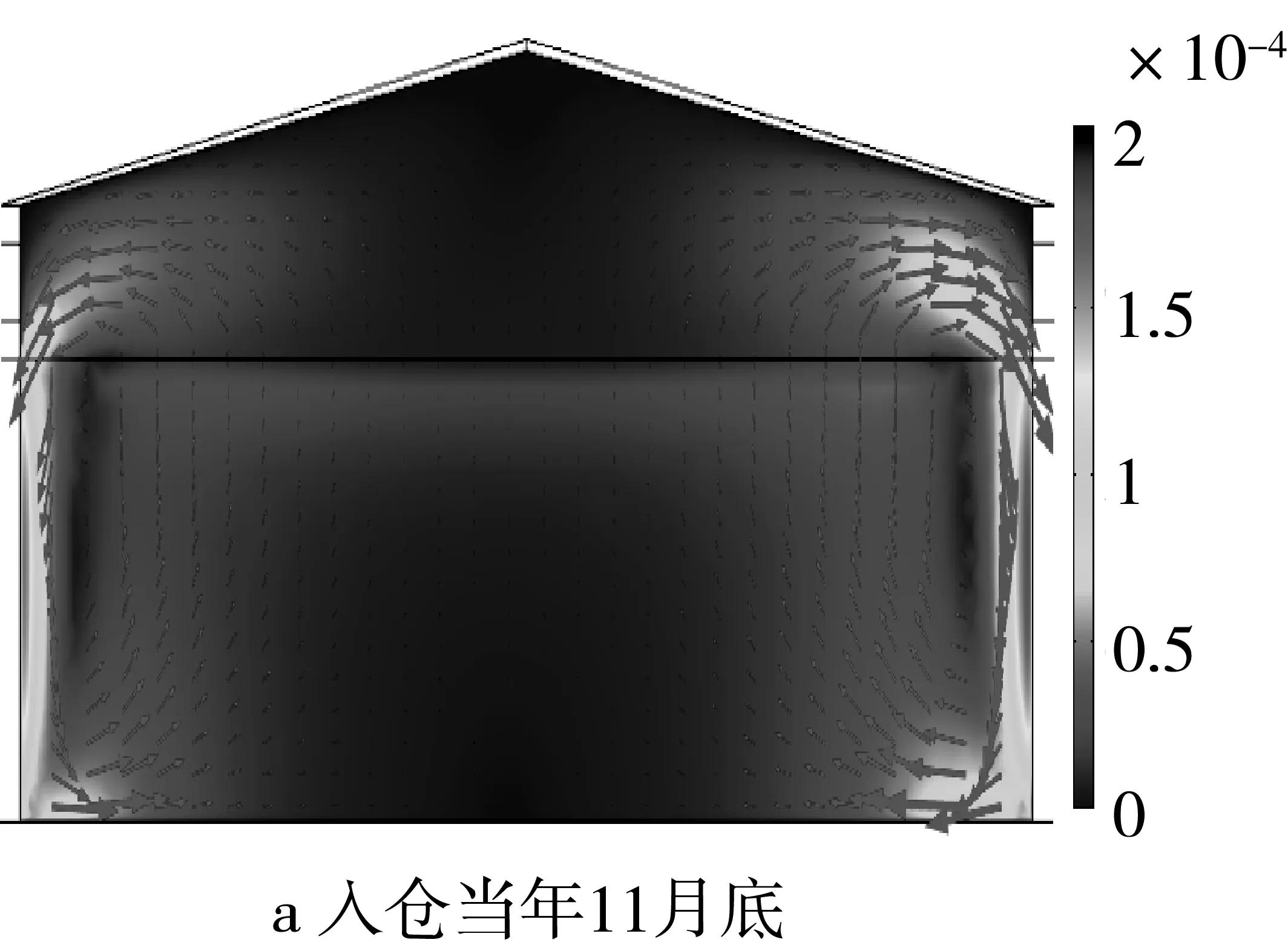
图2 王远成等模拟的跨度22 m粮堆高度5 m房式仓内稻谷的流场分布

1.3 自然对流对传热过程的影响

由前面的分析，我们知道，粮堆内部自然对流强弱的影响因素主要有：仓型结构、粮种物性参数及周围大气温度变化。

1.3.1 仓型结构和粮种的影响

由粮堆内部空气流动的连续性方程[9-11]，可得u/(L/2)～v/H，并假设粮堆温度的变化ΔT～A。根据数学分析原理，将式(1)写成如下形式：

(3)

如果自然对流项数量级非常大或者远大于传导项的数量级，由能量方程[9-11]得到自然对流项和扩散项之间的关系如下式：

(4)

因此，自然对流项数量级大于传导项时，

(5)

将式(5)带入方程(3)，可得

(6a)

同理可得，圆柱坐标下，

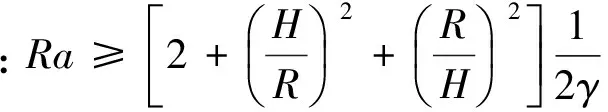
(6b)

对于小麦，当μ/K=3×103，g=9.81，α=1.1×10-7，β=3.4×10-3，γ=9.8×10-4，ρa=1.23以及A=15时，根据式(1)可得，Ra/H=1.86×103。

对于浅圆仓，通过式(6)计算可知：当H/R=1时，如果H>1.1 m；当H/R=1.5，如果H>1.29 m时，粮储过程中自然对流就会大于热传导的作用。若储藏的是玉米的话，Ra/H=5.83×103，当H/R=1时，如果H>0.35 m；当H/R=1.5，如果H>0.41 m时，粮储过程中自然对流(微气流运动)就会大于热传导的作用。

对于房式仓来说，H/(L/2)≈0.5左右，H≈6 m左右。对于小麦来说，H>1.92 m；对于玉米，H>0.61 m，小麦或玉米粮储过程中自然对流(微气流运动)就会大于热传导的作用，而且当粮粒的尺寸较大时，由于渗透率的增加，自然对流(微气流运动)的影响更加明显。由此可以看出，就目前我国的浅圆仓和房式仓储粮条件，都不可忽略自然对流(微气流运动)的影响。

同时，以小麦在房式仓储藏9～10个月(∂t=6960小时)为例，房式仓跨度为12 m，即∂x≈12，装粮高度为6 m，即∂y≈6。期间的平均粮温变化为15 ℃，即∂T=15 ℃，粮堆内部自然对流(微气流运动)的各向平均速度分别为u=2.65×10-5m/s，v=5.14×10-5m/s。粮堆跨度∂x≈12，粮堆高度∂y≈6，∂W=0.000 1 kg，kb=0.133 W/(m·℃)，ρaca=1.23 kg/m3·100 6 J/(kg·℃) ，ρbcb=650 kg/m3·140 0 J/(kg·℃)，hs=2.47×106J/kg，qr=0.15～0.5 W/m3。对能量方程[9-11]进行数量级的数学分析，可以得到：

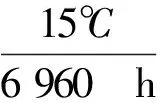
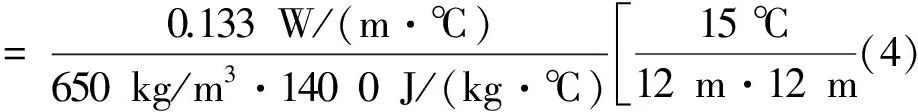
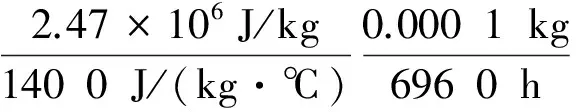
(7a)

即

2.16×10-3(1)+[1.65×10-4(2)+6.39×10-4(3)]=[5.47×10-4(4)+2.19×10-3(5)]+2.5×10-5(6)+(4.17×10-5～1.39×10-4)(7)

(7b)

比较式(7b)中各项数量级大小可以看出，粮堆内部自然对流(微气流运动)对热量传递有一定的影响，不可以忽略，也就是说，粮堆的温度主要是导热(式(7b)中的第(4)、(5)项)和自然对流(式(7b)中的第(2)、(3)项)作用的结果。另外，比较式(7b)中的第(4)、(5)项，可以看出，就导热对热量传递的贡献而言，显然，垂直方向的导热的贡献率大于水平方向的贡献率，也就说，粮堆内部的垂直方向的温度变化高于水平方向。

根据前面的数学分析原理和方法，此时，H/R=2，对于小麦来说，当H>1.72 m时，才需要考虑自然对流；但对于玉米来说，当H>0.55 m时，就需要考虑自然对流。由于该实验工况的粮堆的高度H=0.572 m，显然，储存小麦时，试验仓内部的温度主要受导热的影响，而储存玉米时，则是自然对流和热传导共同作用的结果。

图3和图4分别是王远成等[9]、Khankari[8]模拟的近似冬季和夏季储藏150天时浅圆仓内温度场分布，王远成等[9]采用的是对流扩散模型，而Khankari[8]采用的扩散模型(忽略自然对流作用)，可以看出，两者模拟结果中等温线略有差异。其原因在于，对于热芯粮来说，由于壁面附近和右下角的粮堆内部自然对流较强，加速该处热量扩散，使得该处粮温下降的较快；对于冷芯粮来说，由于壁面附近和右上角的粮堆内部自然对流较强，加速该处热量扩散，使得该处粮温下降的较快。因此可以看出，忽略自然对流作用的影响，会导致数值模拟结果的差异。

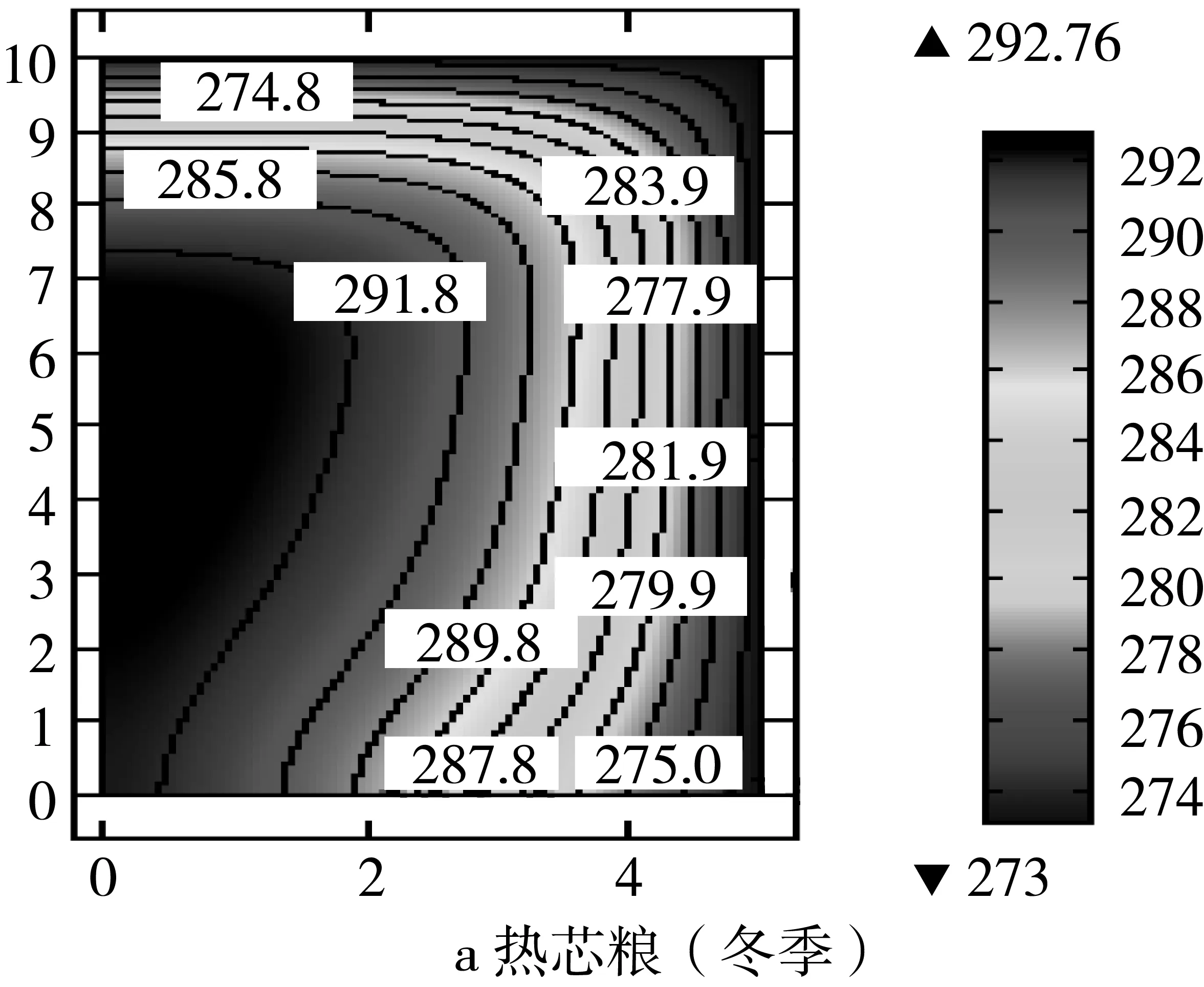
图3 王远成等模拟的近似冬季和夏季储藏150天时浅圆仓内温度场分布

图4 Khankari模拟的近似冬季和夏季储藏150天时浅圆仓内温度场分布

1.3.2 周围大气温度变化的影响

由前所述可知，Ra/H还取决于环境温度Ta和空气温度变化幅度A。图5是数值模拟的两种圆筒仓内储粮平均温度随着瑞利数变化的情况。当粮堆高度与圆筒仓半径不变时，粮堆的温度变化主要随瑞利数改变而改变，而Ra体现了环境温度随时间的变化。如图5所示，一年中的储粮平均温度的最大值，它总是出现在在每一年的第二十八周(夏季期间)，恰好在环境温度的最大值后。当Ra>104时，从图5可以看出，H/R=1的仓的平均温度就开始随着Ra的增大而升高。同样，对于H/R=10的粮仓，当Ra>105时，温度才开始升高。

从图5中还可以看出，随着周围温度的增加，H/R=10的粮仓受周围温度变化产生的影响将会滞后于H/R=1的粮仓。当Ra值较小时，在粮仓中心(r=0,z=H/2)处，热传导控制着热量从周围的高温到中心低温传递。但是，随着Ra增加到大约104，由于自然对流加速了能量的流动，使温度分配更加均匀，这时中心温度会接近于平均值。

图5 不同仓型内粮堆平均温度随瑞利数的变化规律

1.4 自然对流对水分迁移的影响

对同时期粮堆内部水分迁移方程[9-11]进行数量级分析，可以得到：

1.44×10-8(1)+[(1.77×10-11(2)+8.91×10-11(3)]+(5.31×10-9(4)+2.06×10-8(5))

=[(3.17×10-13(6)+1.27×10-10(7)]+[(4.17×10-10(8)+1.67×10-9(9)]

(8)

比较式(8)中各项数量级大小，不难看出，自然对流对(微气流运动)水分迁移影响是明显的，也就说，自然对流(微气流运动)对粮堆内部的水分影响是不可忽略的。图6是Khankari[7]研究得到的自然对流对粮堆内部水分变化的影响规律。从图6可以看出，对于小麦来说，水分迁移主要受扩散作用的影响；对于玉米来说，控制玉米水分迁移过程主要是对流作用。这也说明，对于颗粒粒径较大的粮种，比如玉米，由于其渗透率相对较大，自然对流水分迁移的影响较大。

图6 Khankari实验与数值模拟结果(水分)的比较

1.5 热量传递与水分迁移的耦合关系

从式(8)中各项的数量级大小可以看出，温度梯度对水分迁移影响较大，也就是说，热量传递主导水分的迁移，而对水分梯度的影响相对较小；同时，自然对流也会加剧水分的迁移。比较式(7)和(8)可以看出，粮堆内部热量传递和水分迁移是相互耦合的，对于密闭性较好的粮仓而言，粮堆与仓外的水汽交换较小，粮堆内部平均水分变化率很小，即式(7)中第(6)项非常小，因此，相对而言，热量传递对水分迁移影响较大，而水分迁移对热量传递影响较小。

图7是发生在圆筒仓中心(R=0,Z=H/2)的考虑和不考虑水分迁移影响时圆筒仓中心的储粮温度。从图7发现，与没有水分转移情况相比，有水分迁移时圆筒仓中心的储粮温度值约高0.5 ℃。但随着自然对流的增加，即瑞利数Ra的增大，两者间差异是减少的。

图7 H/R=1时TD和TO分别是考虑和不考虑水分迁移时圆筒仓中心的粮温

1.6 呼吸作用对热量传递的影响

分析式(7)还可以看出，尽管粮堆呼吸产热量相对于其他项较小，即方程(7)中左后一项较小。但对于长期储藏的粮堆来说，粮堆呼吸作用对粮堆内部的热量传递的影响具有累加效应，不可忽略。也就是说，长期储藏的谷物，可能会由于呼吸作用产生的热量而导致粮堆温度的升高，甚至会产生局部发热霉变。图8是储存400 d的房式中稻谷平均温度变化规律，可以看出，谷物呼吸放热会对粮堆内部温度产生一定的影响。

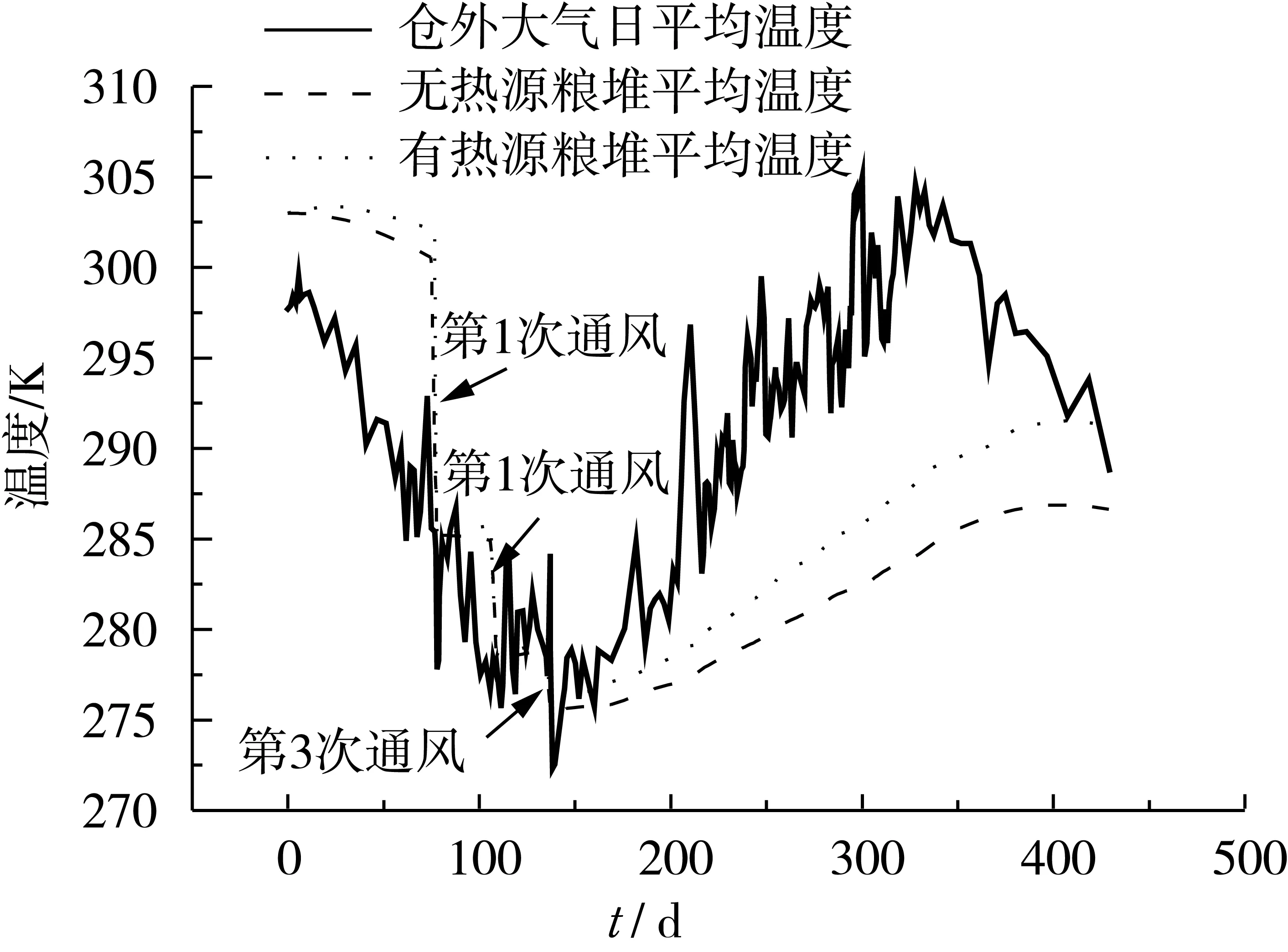
图8 储藏400 d粮堆平均温度随时间变化规律

2 结论

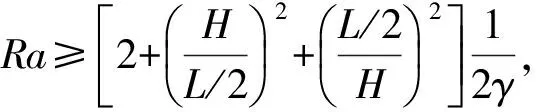
当浅圆仓的装粮高度与半径比为H/R=1.0～1.5，房式仓装粮高度与1/2跨度比H/(L/2)= 0.4～0.56时，自然对流对仓储粮堆内部的温度和水分影响明显，不可忽视。对于粒径较小的谷物(如说小麦)，相对于粒径较大谷物(如玉米)，其内部自然对流作用更强。对于长期储藏的粮堆来说，粮堆呼吸作用对粮堆内部的热量传递的影响具有累加效应，谷物呼吸放热会对粮堆内部温度产生一定的影响。

[1]Converse H H, Graves A H, Chung D S. Transient heat transfer within wheat stored in a cylindrical bin [J]. Transactions of American Society Agricultural Engineering, 1973, 16(1): 129-133

[2]Yaciuk G, Muir W E, Sinha R N. A simulation model of temperatures in stored grain [J]. Agricultural Engineering Research, 1977, 20: 245-258

[3]Jiang S, Jofriet J C. Finite element prediction of silage temperature in tower silos [J]. Transactions of American Society Agricultural Engineering, 1987, 30(6):1744-1750

[4]Jian F, Digvir S, Jayas, et al. Temperature fluctuations and moisture migration in wheat stored for 15 months in a metal silo in Canada [J]. Stored Products Research, 2009, 45:82-90

[5]Beukema K J, Bruin S, Schenk J. Three-dimensional natural convection in a confined porous medium with internal heat generation[J]. International Journal of Heat Mass Transfer, 1983, 26: 451-458

[6]Nguyen T V. Natural convection effects in stored grains-a simulation study [J]. Drying Technology, 1987, 5: 541-560

[7]Khankari K K, Patankar S V, Morey R V. A mathematical model for natural convection moisture migration in stored grain [J]. Transaction of ASAE, 1995a, 38(6): 1777-1787

[8]Khankari K K, Morey R V, Patankar S V. Mathematical model for moisture diffusion in stored grain due to temperature gradients [J]. Transactions of the ASAE. 1994, 37(5):1591-1604

[9]王远成,白忠权,张中涛,等.仓储粮堆内热湿耦合传递的数值模拟研究[J].中国粮油学报,2015,30(11):97-102

Wang Y C, Bai Z Q, Zhang Z T , et al. Numerical study on natural convection heat and moisture transfer in stored grain in a silo [J]. Journal of the Chinese Cereals and Oils Association, 2015, 30(11):97-102

[10]王远成,亓伟,张中涛.圆筒仓内自然对流对粮堆热湿传递的影响研究[J].水动力学研究与进展A,2014,29(4):487-496

Wang Y C, Qi W, Zhang Z T. The effect of natural convection on heat and moisture transfer of stored grain in a silo [J]. Chinese Journal of Hydrodynamics, 2014, 29(4):487-496

[11]Wang Y C, Yang K M, Zhang Z T, et al. Natural Convection Heat and Moisture Transfer with Thermal Radiation in a Cavity Partially Filled with Hygroscopic Porous Medium [J]. Drying Technology, 2016, 34(3):275-286.

Mathematical Analysis and Validation for Natural Convective Heat and Moisture Transfer in Grain Bulk During Sealed Storage

Wang Yuancheng1Pan Yu1Yu Yaofang1Wei Lei2Zhang Zongjie2Zhao Huiyi2Shi Tianyu2Yin Jun2
(Thermal Engineering school, Shandong Jianzhu University1, Jinan 250101)(Academy of State Administration of Grain2, Beijing 100037)

In present paper, the physical meaning and order of magnitudes in all equations were analyzed by mathematical analysis, and the relationship between natural convection, heat and moisture transfer processes was examined based on the mathematical models of natural convection and coupled heat and moisture transfer in the grain bulk. The rayleigh number and its influence factors were proposed to determine the condition of natural conversion in the grain bulk. The influence of barn structure, grain species and air temperature outside the barn on the natural conversion, heat transfer and moisture migration was analyzed, and the analysis results were verified by the numerical modeling. The results showed that matheametical analysis method is an effitive approach to analyze natural conversion, heat transfer and moisture migration in the grain bulk. The results of matheamatical analysis can provide reference for barn type design, simulation of grain storage ecosystem and warehouse technology management.

matheamatical analysis, grain bulk, natural convection, heat transfer, moisture migration

TK121; TS207.7

A

1003-0174(2017)09-0120-07

国家自然科学基金(51276102),国家重点研发计划(2016 YFD0400100, 2016YFD0401002),国家粮食公益专项(201513001)

2016-06-21

王远成，男，1963年出生，教授，复杂系统流动和传热传质