电控柴油机燃油系统参数匹配对油耗率的影响

孙思远， 徐 虎， 黄加亮,2 ， 胡启坤

(1.集美大学 轮机工程学院， 福建 厦门 361021； 2.福建省船舶与海洋工程重点实验室， 福建 厦门 361021； 3.上海海事局， 上海 200086)

2017-05-22

国家自然科学基金(51279066)；福建省自然科学基金(2017J01486)

孙思远(1991—),男,山东济宁人，硕士生,研究方向为柴油机性能优化与排气测试分析。 E-mail: 471100179@qq.com

黄加亮(1963—)，男，福建南安人,教授，博士，从事船舶柴油机性能优化与故障分析研究。E-mail:1073535007@qq.com

1000-4653(2017)03-0014-06

电控柴油机燃油系统参数匹配对油耗率的影响

孙思远1， 徐 虎1， 黄加亮1,2， 胡启坤3

(1.集美大学 轮机工程学院， 福建 厦门 361021； 2.福建省船舶与海洋工程重点实验室， 福建 厦门 361021； 3.上海海事局， 上海 200086)

基于某船用四冲程柴油机的电控化改造，利用AMESim及AVL_FIRE软件建立电控组合泵单缸燃油喷射系统模型和缸内高压循环模型。采用一次回归正交试验设计方法对燃油喷射系统参数进行优化匹配和显著性检验;采用二次回归正交试验设计方法对优化结果与油束夹角进行匹配优化。结果表明:初优化得到的三组参数组合都满足设计压力为105 MPa的要求；再优化得到的8个×0.26 mm-15.0 mm-0.46 mm/(°)-900 mm-150°(喷孔数×孔径-柱塞直径-凸轮型线速度-油管长度-油管直径-油束夹角)参数组合下的油耗率最低为0.191 0 kg/(kW·h)；通过回归分析得到的油耗率预测模型可准确预测油耗率，使研究周期大大缩短。

船舶工程;柴油机；电控化改造；正交试验设计；燃油系统；参数优化；油耗率

近年来，随着全球经济持续低迷，能源紧缺问题不断加剧，燃油费用占船舶总成本的比例逐步提高(已高达40%～50%)，降低船舶燃油消耗成为降低海上运输成本的一项重要措施。[1]在直喷式四冲程柴油机中,燃油系统喷油压力是评价缸内燃油燃烧是否良好的重要指标，提高燃油喷射压力可解决缸内雾化问题，但会增大燃油碰壁的可能性，并影响喷注的形成及缸内气体的流动。由于影响燃油喷射系统工作性能的结构参数较多,因此必须在影响较大的主要结构参数之间作出最优选择和匹配。[2]对此,在高强化条件下组织良好的油气混合和燃烧过程，合理地在喷油系统各参数之间进行匹配十分必要。这里利用AMESim及AVL_FIRE软件建立电控泵燃油喷射系统模型和缸内高压循环仿真模型，结合一次回归正交设计和二次回归正交设计的试验方法对喷油参数进行优化,以降低柴油机的油耗率，进一步提高柴油机的经济性。

1 电控组合泵燃油系统的组成及原理

电控组合泵燃油系统(见图1)由电控部分和机械液力部分组成，其中电控部分的“感觉神经”——传感器将柴油机的滑油温度、冷却水温、中冷器前后温度、转速和缸内压力等关键运行参数迅速准确地传输给电控部分的“大脑”——电子控制单元(Electronic Control Unit,ECU)，通过ECU内部存储的MAP图和ECU收集的信号控制电控单体泵电磁阀(见图2)的通电及断电，通电的电磁阀对衔铁产生电磁吸合力，带动控制杆关闭密封面，此时机械液力部分的凸轮继续上行对柱塞进行加压，使高压油管建立高压;当油管中的油压大于喷油器针阀背压时，燃油立即喷入气缸;当完成喷油工作时，ECU断电，电磁阀回位，泄油孔被打开，余下的燃油回流油箱，完成一次喷油过程。[3-4]

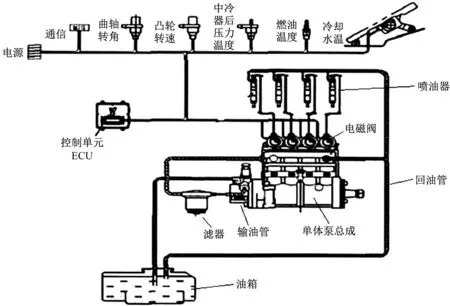
图1 电控组合泵燃油喷射系统

2 电控组合泵燃油喷射系统参数一次优化

2.1电控组合泵燃油喷射系统仿真模型建立与验证

电控组合泵单缸燃油喷射模型由单体泵模块、喷油器模块和电磁阀模块等3大模块组成，通过系统内部的油管将其连接成一个集机械、电磁和液压于一体的完整仿真系统。图3为燃油喷射系统模型，在初步完成系统草图的设计之后，结合各仿真模块的数学模型及系统相关结构、运行参数来设置仿真模型的模块参数。系统主要参数见表1。

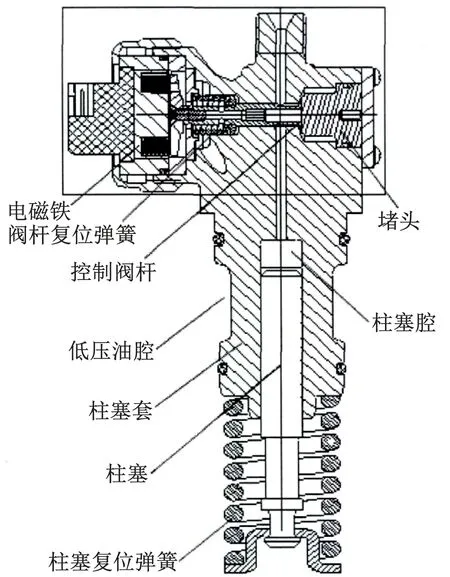
图2 电控组合泵结构简图

图3 燃油喷射系统模型

在利用试验数据验证仿真模型的准确性和稳定性之后，仿真模型才能为喷油特性仿真研究提供可靠的依据。图4为额定转速为1 000 r/min(凸轮转速为500 r/min)，喷孔直径为0.26 mm，油管长度×直径为900 mm×2.0 mm，凸轮型线速度为0.46 mm/(°)，喷油脉宽为14时，仿真曲线(喷油速率、嘴端压力)与试验数据对比,仿真值与试验值之间存在一定的误差：喷油速率误差为0.5 mm/(°)；嘴端压力误差为2.3 MPa；两者误差≤5%。试验曲线与仿真曲线基本吻合，说明所建仿真模型能较为准确地预测喷油规律。

2.2一次回归正交试验设计

对燃油喷射系统参数进行匹配研究的目的是：在保证燃油循环喷射量为650～750 mm3的同时，提高燃油喷射的压力,使其≥105 MPa，为燃油在缸内燃烧提高燃油雾化效果做准备。影响燃油喷射压力的燃油系统结构参数主要有柱塞直径、凸轮型线速度、油管长度、油管直径、喷孔数及喷孔直径。各因素的变化范围及水平编码见表2。

表1 电控单体泵燃油喷射系统主要参数

a) 嘴端压力

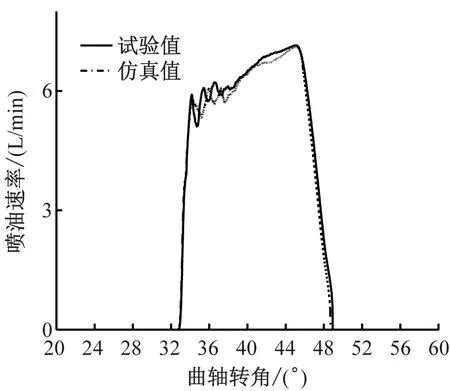
b) 喷油速率

表2 各因素的变化范围及水平编码

表3为试验方案及试验结果，通过查询正交表，确定5因素、2水平的正交试验表，共8次试验。由试验数据可知：以喷油压力为优化目标,2号试验得出的喷油压力较大，3号试验得出的喷油压力较小，柱塞直径和凸轮型线速度选取下水平，说明单位时间作用的凸轮转角变小，油泵供油压力和供油量都变小，油管长度选取上水平，造成油液到达嘴端时压力损失偏大，最终造成3号试验结果，但试验结果在可控范围内，从下面的显著性验证中可得出。

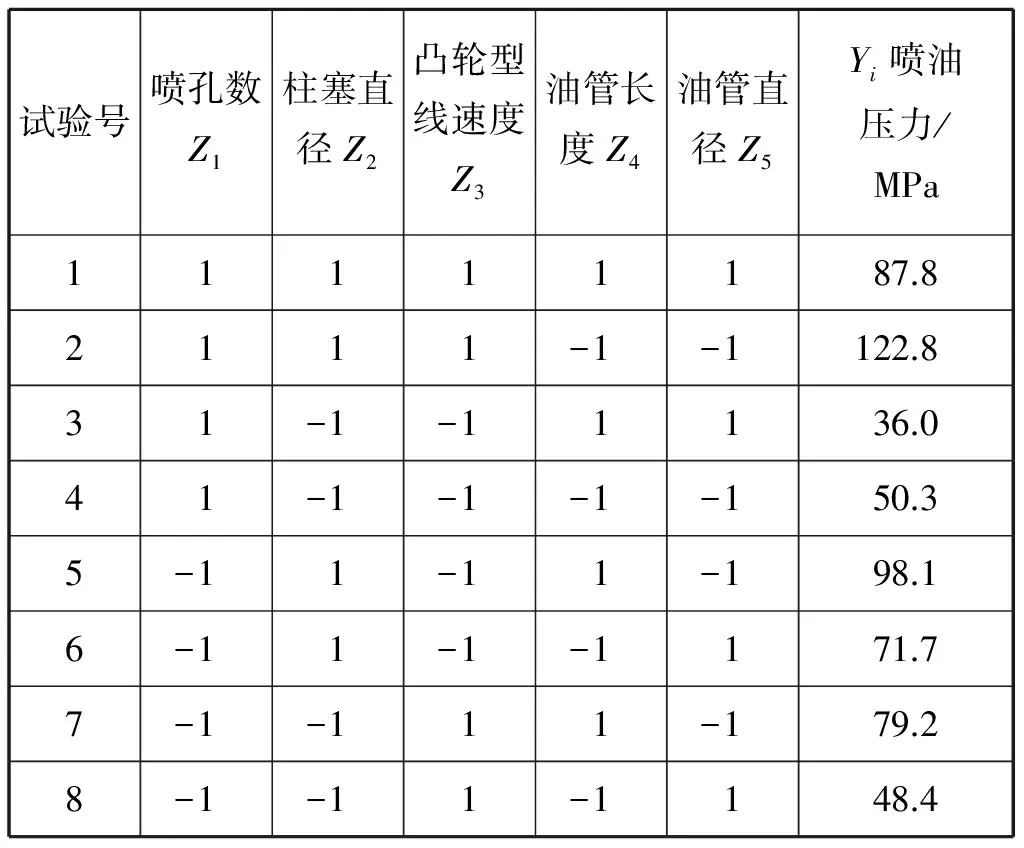
表3 试验方案及试验结果

只有通过合理的试验设计得到大量试验数据，并对试验数据作进一步的计算分析和处理,才能对研究的问题有明确的认识，从中寻找到规律性信息。[5]这里运用Excel软件【数据分析】模块建立一次回归方程,即

Y=-242.47-1.562 5X1+13.875X2+

342.08X3+0.009 875X4-13.312 5X5

(1)

通过回归方程因素的方程系数可知，因素X2,因素X3和因素X5对试验指标的影响比较大，因素X1和因素X4对试验指标的影响很小，即柱塞直径和凸轮型线速度增大、油管直径减小,喷油压力可得到很大的提高，在保持喷空通流面积不变的情况下，喷孔数和油管长度对喷油压力的影响很小。

对于得出的回归方程,可通过显著性验证来说明其可信度。对回归方程的显著性进行检验,反映回归方程在试验点上与试验结果的拟合是否良好。

表4和表5分别为方差分析参照表及方差分析数据表。从表5中可看出，因素Z2，因素Z3和因素Z5对试验指标Y有非常显著的影响，说明柱塞直径、凸轮型线速度及喷孔直径对喷油压力的影响非常显著，而所建立的回归方程也非常显著，反映出所得的回归方程在预先制订的试验点上与试验结果拟合较好。图5为试验值与回归方程预测值的对比。由图5可知，回归方程预测的结果可作为初步预测燃油喷射系统喷油压力的参考，从而大大提高研究效率，缩短研究时间。

表4 方差分析参照表

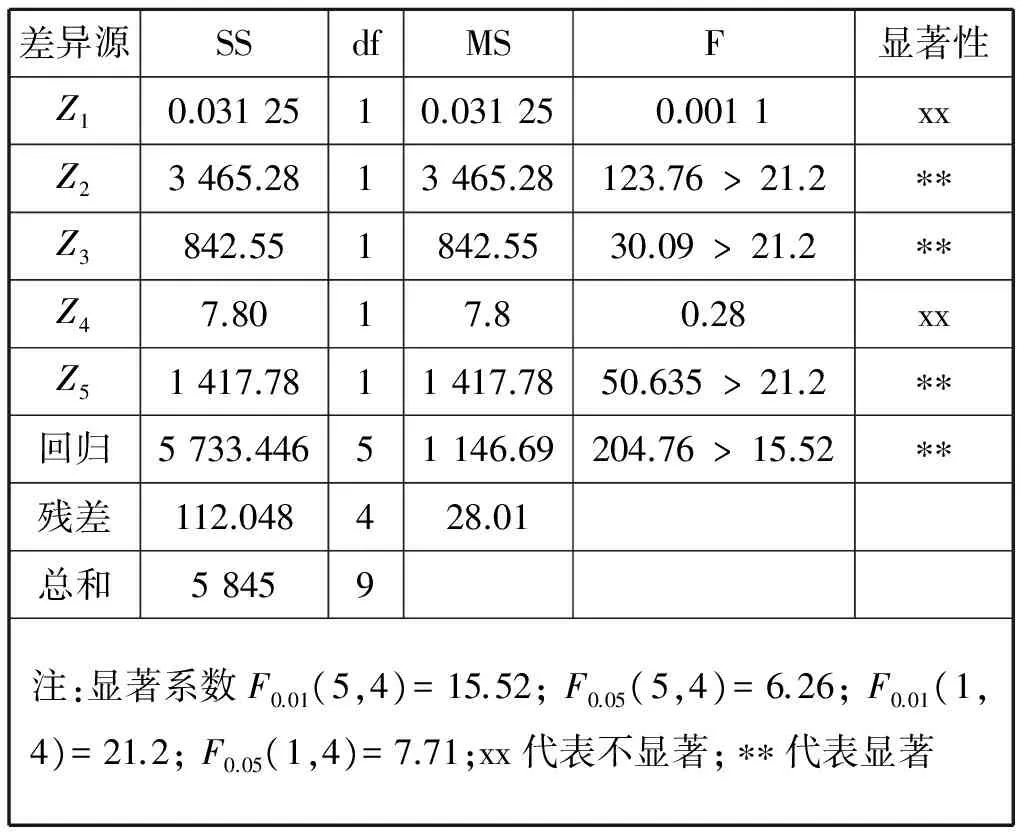
表5 方差分析数据表

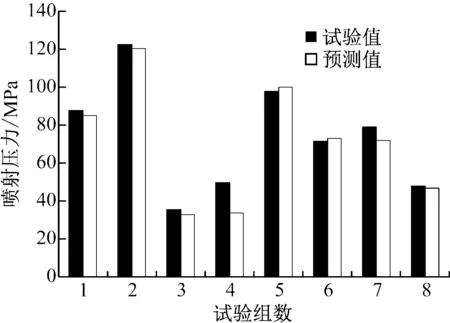
图5 试验值与回归方程预测值的对比

为提高燃油喷射压力，在回归方程的基础上进一步缩小寻优范围。由以上分析可知：柱塞直径和凸轮型线速度可选取取值范围内的最大值，即15 mm，0.46 mm/(°)；油管长度选取原长度900 mm；喷孔数对燃油在缸内燃油的分布有很大影响，因此选取6个×0.30 mm，8个×0.26 mm和10个×0.22 mm等3种喷油器。油管直径选取1.4 mm和1.2 mm作进一步的试验。

表6为优化参数试验的安排及结果。由表6可知，B,C,F等3组的喷油压力达到试验目标>105 MPa的要求，喷油量满足650～750 mm3的要求。因此,选取B,C,F等3组燃油参数组合为最佳匹配参数组合，为与油束夹角匹配进行缸内燃烧计算做准备。

表6 优化参数试验安排及结果

3 电控组合泵燃油喷射系统参数二次优化

3.1缸内燃烧模型的建立与验证

燃油喷射过程是柴油机工作过程中极为重要的组成部分，喷射过程组织的好坏直接影响油束与空气在燃烧室中的混合，进而影响缸内燃烧过程的组织。油束夹角作为缸内燃烧过程的一个重要参数，对柴油机油耗率有着重要影响。现将油束夹角与得到的3组优化参数相匹配，基于AVL_FIRE软件对缸内高压循环进行仿真，结合二次正交回归试验设计得到最佳的燃油系统喷射参数，使柴油机的油耗率最低。

通过实测某型船舶四冲程柴油机燃烧室各结构的尺寸，利用AUTO-CAD软件画出燃烧室1/2横剖面模型，将该模型转换成DXF格式导入到AVL-FIRE软件中的柴油机缸内高压循环ESE模块中。在ESE模块中，软件可自动快速生成网格，由于研究对象的对称性，根据喷油器喷孔数n，选择燃烧室计算区域为整个燃烧室的1/n(见图6)。

图6 燃烧室部分区域剖面图

将通过原机试验平台的缸压传感器得到的缸压曲线与仿真计算得到的二维缸压曲线相对比,二者虽稍有偏差，但在误差允许的范围内，保持在5%以内，说明所建立的仿真模型是正确的(见图7)。[6]

图7 仿真计算缸内压力与试验所得缸压对比

3.2基于二次回归正交设计法的燃烧参数匹配

利用二次回归正交试验设计方法在各因素水平范围内寻优，以油耗率为目标建立二次回归方程，选取油束夹角和喷孔数作为因素进行匹配，并通过规划求解计算出对应于最低油耗率的最优燃烧系统参数组合。由于影响油耗率的燃油系统喷射参数不是独立的，因此要考虑各因素之间的交互作用,各因素参数水平见表7。

表7 各因素参数水平

回归正交组合由二水平试验、星号试验和零水平试验组成[7]，其中:二水平试验次数为mc,mc=2m(m为因素数)，即mc=4；星号试验次数只与试验因素数有关，为mγ=2m=4；零水平试验只进行1次，也可进行多次,记m0=2，总试验次数为n=mc+mγ+m0=10。其因素水平编码见表8。

表8对各因素的各水平进行线性变换，变化后使各因素的各水平在编码空间内是“平等”的[8],不受各因素水平单位及数值大小的限制，都在[-1,1]内变化。表9为试验方案与计算结果，其中:Z1和Z2分别为喷孔数及油束夹角的规范变量;yi为仿真出的油耗率，kg/(kW·h);第9号和第10号试验为零水平试验。

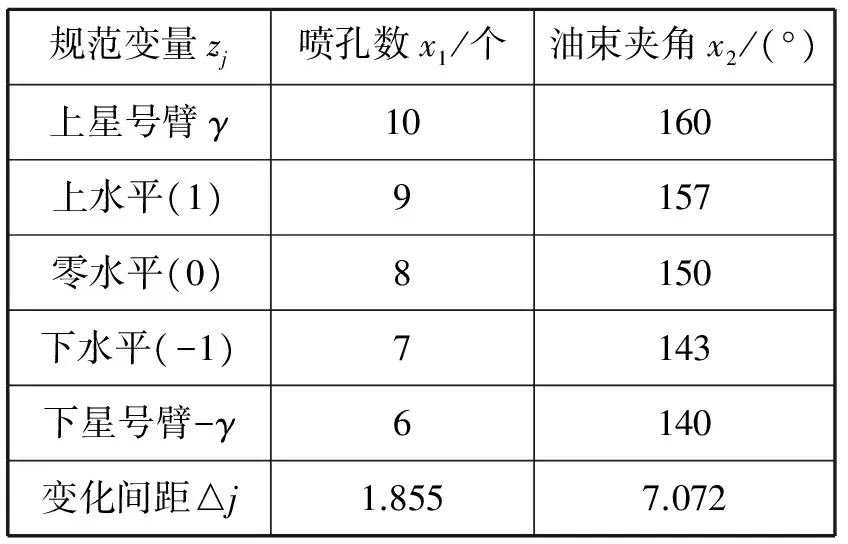
表8 因素水平编码

根据表7，通过计算得出以油耗率为目标的回归方程为

y=a+b1Z1+b2Z2+b12Z1Z2+b11Z12+b22Z22

(1)

(2)

由此可得出规范变量与油耗率之间的回归方程为

(6)

通过二次回归正交试验得到规范变量与油耗率之间的回归方程，将表9中的10组燃烧系统参数代入到该回归方程中,将所得的油耗率与表9中的仿真计算值相对比。图8为油耗率回归方程试验值与预测值的对比。由图8可知,表9中油耗率的仿真计算值与回归方程预测值大小相近，说明所建回归方程模型误差不大，可实现预测的功能。

利用Microsoft Office Excel 2007中【数据】模块中的规划求解功能对燃烧系统参数和油耗率进行求解，得到的最优解为最低油耗率对应的参数组合：喷孔数为8个，油束夹角为150°。

将优化参数8个×0.26 mm-15.0 mm-0.46 mm-900 mm/(°)-1.4 mm与油束夹角150°代入到AVL-FIRE软件中进行缸内计算，优化试验结果如表8所示。油耗率优化目标仿真试验与数学模型预测值对比见表10。

表9 试验方案与计算结果

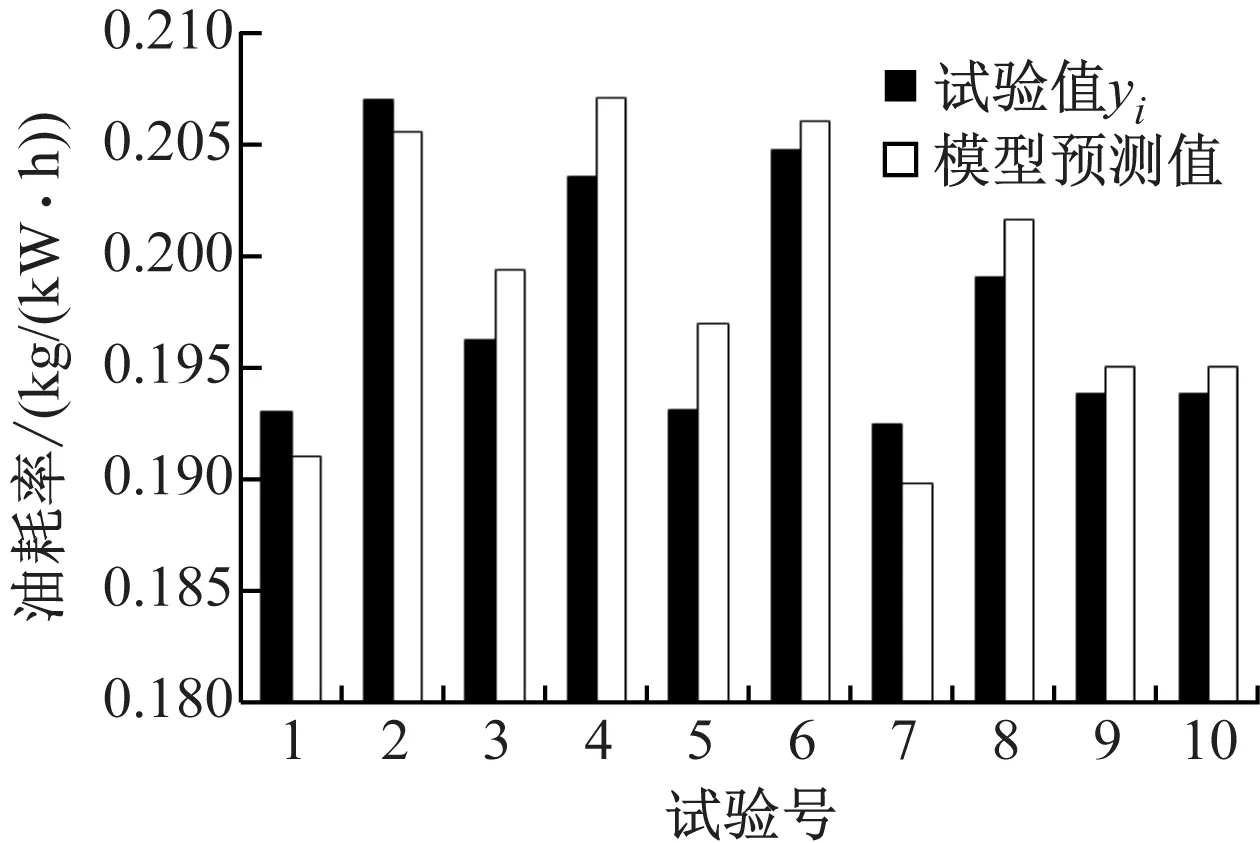
图8 油耗率回归方程试验值与预测值对比

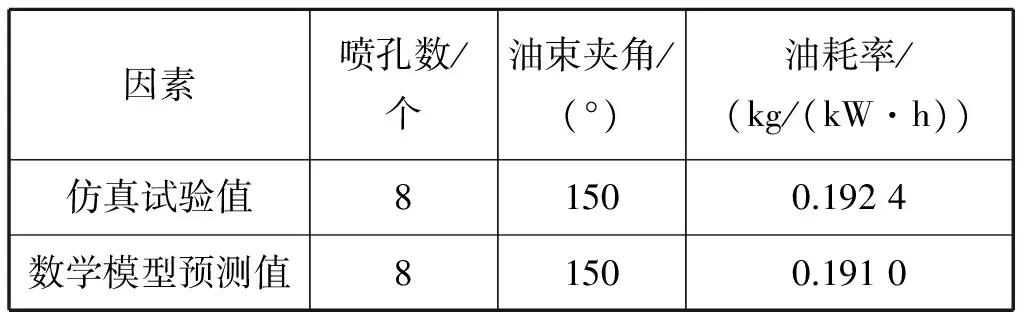
表10 油耗率优化目标仿真试验值与数学模型预测值对比

由表10可知，利用二次正交回归设计方法得到的以油耗率为优化目标的预测优化结果与试验仿真值之间的误差较小，相对误差保持在3%以内，模型可实现对油耗率的准确预测。

4 结束语

1) 基于某船用四冲程柴油机的电控化改造，应用一次回归正交设计方法和AME-SIM仿真软件进行电控泵燃油系统参数的仿真计算。以提高燃油喷射压力为目标分析建立的回归方程可知：柱塞直径和凸轮型线速度增大、油管直径减小可很大程度地提高喷油压力，并得到3组优化参数组合，即10个×0.22 mm-15.0 mm-0.46 mm/(°)-900 mm-1.4 mm,8个×0.26 mm-15.0 mm-0.46 mm/(°)-900 mm-1.4 mm;6 mm/(°)×0.30 mm-15.0 mm-0.46 mm/(°)-900 mm-1.4 mm(喷孔数×孔径-柱塞直径-凸轮型线速度-油管长度-油管直径)，满足电控组合泵燃油喷射匹配设计压力的要求。

2) 选取一次优化得到的3组参数与油束夹角匹配，并运用二次回归正交试验设计方法进行优化，得出8个×0.26 mm-15.0 mm-0.46 mm/(°)-900 mm-1.4 mm与油束夹角150°匹配油耗率最低，最低油耗率为0.191 0 kg/(kW·h)，且建立的以油耗率为优化目标的数学模型的预测值与仿真试验值的误差<3%，说明二次回归正交试验设计建立的油耗率预测数学模型是可行的。

[1] 黄少竹. 船舶柴油机[M]. 大连：大连海事大学出版社，2005.

[2] 顾力强，黄震.高速柴油机燃油喷射系统结构参数优化设计的计算机仿真[J]. 内燃机工程，1999(2):59-64.

[3] 马智荣. NJ2机车电子燃油喷射系统[J]. 机车电传动, 2010(2):15-17.

[4] 范立云,宋恩哲,李文辉,等.电控组合泵低压系统压力动态特性研究[J]. 内燃机学报，2010,28(2):147-154.

[5] 王文萍. 四因素混合水平正交试验设计[J]. 科技信息，2010(23):659.

[6] 胡启坤，陈杰，黄加亮. 双卷流燃烧室与燃油喷射系统匹配对柴油机排放的影响[J]. 船舶工程，2015(8): 21-24.

[7] 李云雁，胡传荣. 试验设计与数据处理[M]. 北京：化学工业出版社，2005:132.

[8] 杨剑秋，王廷荣. 基于正交试验设计的空心叶结构优化设计[J]. 航空动力学报，2001,26(2): 376-384.

InfluenceofOptimalMatchingofFuelInjectionSystem’sParametersonFuelComsumptionofDieselEngine

SUNSiyuan1,XUHu1,HUANGJialiang1,2,HUQikun3

(1. Marine Engineering Institute, Jimei University, Xiamen 361021, China； 2. Fujian Provincial Key Laboratory of Naval Architecture and Ocean Engineering, Xiamen 361021, China; 3. Shanghai Maritime Safety Administration, Shanghai 200086, China)

Based on the engine fuel injection system for electronically-control transformation of a 4-stroke diesel engine, the unit cylinder fuel injection system model of electronically-controlled unit pump and the model of high pressure circulation in cylinder are respectively built by means of the software AMESim and AVL_FIRE. Multiple parameters are tested and optimized by means of the linear regression orthogonal experiment design method. The experiment is verified by the significance test. Quadratic regression orthogonal experiment design method is used to match the above optimized results with oil beam angle. Research results show that three sets of parameter combination optimization that gained through the linear regression orthogonal experiment design method can meet the requirements of 105 MPa. The fuel consumption rate can reach the lowest level of 0.191 0 kg/(kW·h) under the parameter combination optimization of 8×0.26 mm-15.0 mm-0.46 mm/(°)-900 mm-150°(number of nozzle holes×bore diameter-diameter of plunger-cam type linear velocity-tubing length-tubing diameter-oil beam angle) which are gained through re-optimization. Quadratic orthogonal regression design method provides a sound basis for fuel consumption rate prediction, greatly shortening the research period.

ship engineering; diesel engine; electronic-controlled transformation; orthogonal experimental design; fuel oil system; parameter optimization; oil consumption rate

U664.121

A