基于Maklink图和蚁群算法的航线规划

陈 晓, 戴 冉, 陈昌源

(大连海事大学 航海学院， 辽宁 大连 116026)

2017-05-03

陈 晓(1993—)，男，山东烟台人，硕士生，主要从事交通信息工程及控制、水上交通安全保障研究。

E-mail: chenxiao19930604@163.com

戴 冉(1964—),男,浙江杭州人,教授,硕士生导师,主要从事船舶性能测试技术、船舶模拟操纵技术、港口工程论证、天文航海等领域的研究。E-mail:dairan@163.com

1000-4653(2017)03-0009-05

基于Maklink图和蚁群算法的航线规划

陈 晓, 戴 冉, 陈昌源

(大连海事大学 航海学院， 辽宁 大连 116026)

为实现航线自动规划设计，提出一种可行的计算方法，并对船舶实际运营中进行航线规划时需注意的问题进行分析。以路径最短为目标，建立以避开障碍物区域和危险区域、控制转弯角度及减少转向点数目等为约束条件的规划模型。在建立模型过程中,采用Maklink图和Dijkstra算法生成初始规划路径，采用蚁群算法对路径作进一步的优化和调整，以满足约束条件。试验结果表明：与传统的在纸质海图上绘制航线及在电子海图上手动输入转向点生成航线相比，通过智能算法生成航线具有耗时短、经济可靠等优点。

船舶工程;航线自动规划；Maklink图；Dijkstra算法；蚁群算法

航线规划是航海活动中的重要环节，随着电子海图系统的广泛应用，自动化的航线设计逐渐成为电子海图系统应用中的重要内容。最优航线设计是指在进行航海活动之前，在考虑水深、障碍物及禁航区等因素的条件下，设计出一条安全的最短航线。但是，在进行海上避难、海上搜救等应急活动时，需更加灵活地选择航线。因此，安全、可靠、快速的航线设计是现代航海的关键。[1]目前，航线规划的方式主要有以下2种：

1) 通过查阅相关资料分析航行要求，在纸质海图上选取转向点，手工绘制航线。

2) 将选取的转向点输入到电子海图显示与信息系统(Electronic Chart Display and Information System,ECDIS)[2]中，生成相关航线，并利用电子海图系统辅助分析航线的可行性。

随着船舶智能化的推进，自动、快速绘制最短航线已成为目前急需解决的问题，而传统的航线设计方式难以满足当前的需求。因此，利用现有的电子海图系统，通过对已有算法进行改进，快速规划出一条安全、可靠的最短航线，对航海活动智能化的发展具有很好的促进作用。

这里利用Maklink图论对海图进行处理，生成无向网络图;通过蚁群算法对Dijkstra算法进行优化，自动搜索障碍物，并在保证安全的前提下自动生成最短计划航线。

1 海图模型建立

对于需规划的海图区域，不能直接使用海图上的水深、障碍物及危险区域等信息,需对这些信息进行建模。通过建模将船舶航行区域转换为Maklink图，在Maklink图的基础上生成无向网络图，并进行下一步的路径规划研究。

1.1安全水深区的提取

准确计算出船舶可安全航行的水域是自动化航线设计的前提。提取安全等深线是ECDIS的一个重要功能，可根据船舶实际吃水确定安全水深区及危险水深区[3]，这里选择在安全水深区进行自动航线规划。

1.2Maklink图论[4-6]

Maklink图论是用来构造自由空间的一种方法，需预先定义凸多边形，将空间分割成自由空间和障碍空间2部分，然后利用定义的基本形状构造自由空间，最后将构造的自由空间表示成全局连通图，在该图上进行路径规划。

空间模型的构造方法为：定义障碍物为凸边形，将任意2个障碍物之间不与障碍物相交的顶点的连线及障碍物顶点与边界相交的线定义为Maklink线，取起点、终点及Maklink线的中点，三点相连构成的无向网络图即为可自由移动的路径。

1.3无向网络图构建

首先对所选用海图中的安全水深区内的海岛、禁航区及危险区域等建立扩展的凸多边形；然后以凸多边形的各顶点为基础构造Maklink图；最后将起点、终点及Maklink线上的中点相连，构造出无向网络图，实现海图模型的建立。

将电子海图中显示的危险区域及障碍物等转换为凸包问题，利用Graham算法[7]生成凸多边形，并在该凸多边形的基础上向外扩展h(见图1)。将所扩展的区域定义为保护区，在路径规划过程中，即使沿着障碍物区域边界寻找最短路径，也能确保运动的船舶不与障碍物发生碰撞。

图1 扩展保护区示意

在凸多边形的基础上，按照以下步骤[6]生成Maklink线，建立Maklink图。

1) 将所有凸多边形的顶点组合成集合D={d1,d2,d3,…,dn}，作顶点到边界的垂线，将所有点两两相连，并按从短到长的顺序排列，存储在集合L中。

2) 选取集合L中的第1条线段。

3) 判断所选线段是否与凸多边形的边界相交。若相交，则该线段不能作为Maklink线，放弃该线段并检查集合L中的下一条线段，直到所检查出的线段不与凸多边形边界相交，进入步骤4)。

4) 检查该线段与凸多边形的顶点产生的2个外角。若2个外角均<180°，则为最佳连接线，删去该顶点的其他连接线，进入步骤7);若某个外角>180°，则将该连接线加入到该顶点的候选连接线中。

5) 检查该顶点的所有候选连接线中是否存在外角>180°。若存在，则选择集合L中的下一条线段，并返回步骤3)；若不存在，则进入步骤6)。

6) 删除该顶点其他冗余的连接线。

7) 重复步骤1)～步骤6),直到完成所有顶点。

在构建完Maklink图之后，选取所有Maklink线上的中点，连接相邻中点、起点和终点，就构成无向网络图。

2 航线规划数学建模

进行航线规划的目的是避开障碍物，并使航行路径最短。因此，结合实际操作需要，还应考虑船舶航向变化的大小及转向点的多少等因素。这里对改变航向的角度、转向点数量等进行约束，并建立相应的数学模型。假设所需规划的航线的转向点序列为(d1,d2,d3,…,dn), 建立数学模型

(1)

s.t.(di,di+1)∩Sj=φ,i=1,…,n,j=1,…,m

(2)

θ≤90°

(3)

h≥hmin

(4)

式(1)～式(4)中：式(1)表示所取转向点间的距离最短，l为两点间的距离；式(2)表示海图中的障碍物区域，约束所取的转向点不在障碍物内；式(3)表示航向改变的角度≤90°；式(4)表示对海图中实际障碍物的扩展距离≥hmin。

3 路径规划

建立海图模型，得到包含起点和终点的无向网络图，这里利用构造的无向网络图，依次进行初始航线规划、蚁群算法优化及路径调整。

3.1初始路径规划

利用Dijkstra算法[8]在无向网络图中选点，所选取的点与路径的起点和终点构成次优路径上的点。

Dijkstra算法的基本思想是按照路径长度的增加顺序寻找最短路径，通过对路径长度进行迭代得到从起点到终点的最短路径。

设路径的起点为S，终点为T，矩阵V存储所有顶点，矩阵W存储相邻两点间的距离，W[a,b]为a和b两点间的距离。对于无向网络图中的每个顶点标号(dt,Pt)，dt表示从起点S到点t的距离，Pt表示从点S到点t的最短路径的前一点。Dijkstra算法流程见图2。

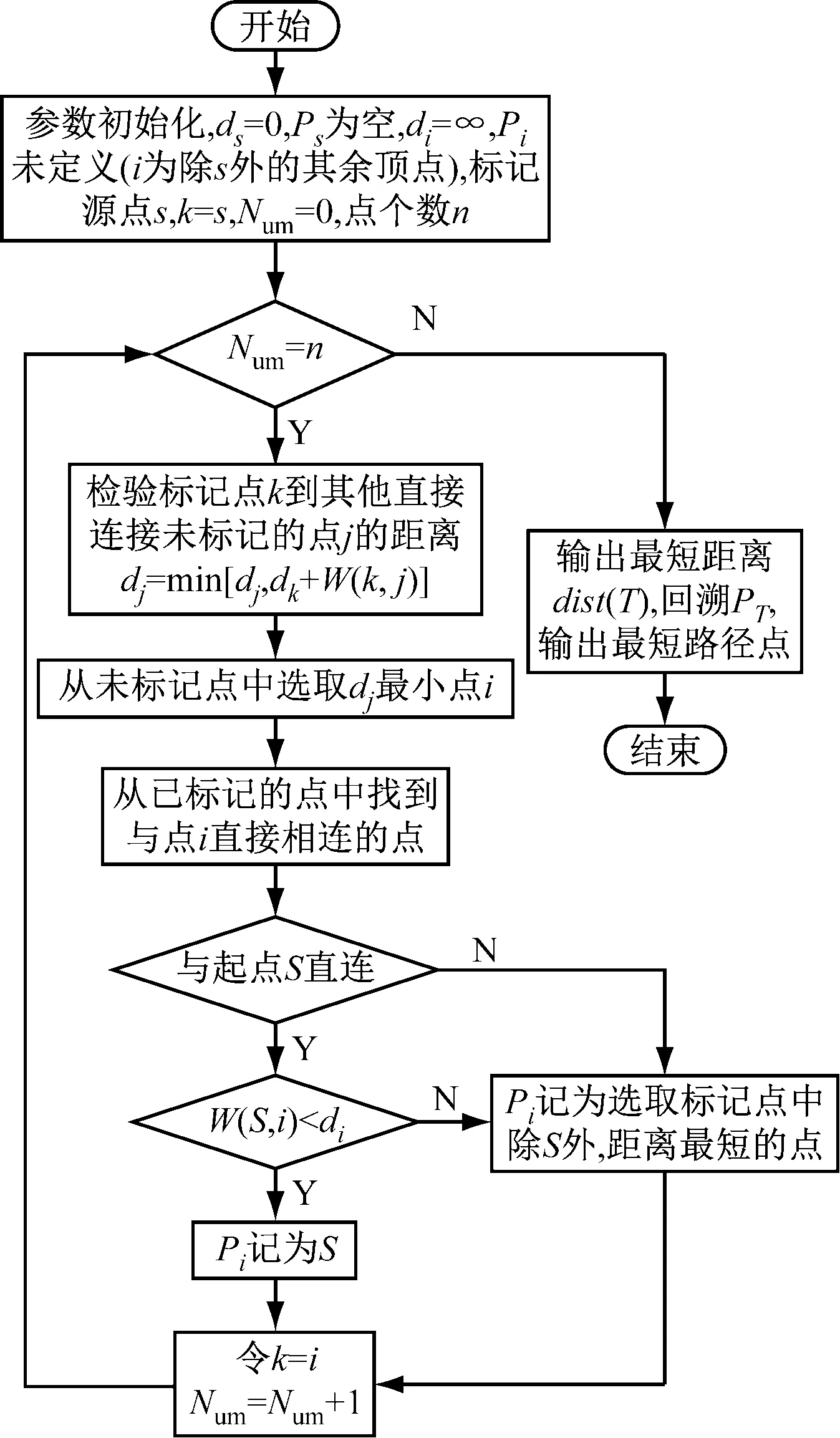
图2 Dijkstra算法流程

图3为Dijkstra规划路径，其中:虚线为Maklink线;黑细实线依次相连构成无向网络图;黑粗实线为通过Dijkstra算法生成的最短路径,途经的路径点为P1,P2,P3,P4。

3.2路径优化

应用蚁群算法[9]对利用Dijkstra算法生成的初始路径作进一步优化，所获得的路径为该Maklink图中距离最短的路径。

3.2.1解的表示形式

图3 Dijkstra规划路径

Li上的其他点可表示为

hi∈[0,1],i=1,2,…,d

(5)

式(5)中:hi为比例参数;d为路径上的节点数。

根据不同的参数hi，可得到一条新的路径，蚁群算法的解可表示hi，即利用Dijkstra算法得到的路径点，调整每个点在Maklink线上的位置，找到一条距离最短的线。为保证算法的可解性，采用固定距离划分法对Maklink线进行划分，设划分长度为ω，每条Maklink线Li的划分数为

(6)

式(6)中:当Int(Li/ω)为奇数时，Maklink线的中点也应为一个分段点，故划分数应为ci+1。由于每条Li都被ci等分，因此Li-1到Li共有ci+1个节点可选择。

3.2.2节点的选择方法

利用蚁群算法优化路径是指寻找参数集合(h1,h2,h3,…,hd)，从而得到距离最短时各节点的位置坐标。假设蚂蚁的数量为m，起点为S，终点为T，其循环的路径为

S→n1j→n2j→…→ndj→T

(7)

式(7)中:ndj为第d条Maklink线上的第j个等分点。每只蚂蚁在选择下一条Maklink线上的等分点时采用的方法为

(8)

式(8)中:I为Maklink线上等分点的集合；i为选择的Maklink线；q为[0,1]内的随机数;q0为[0,1]内的可调参数，为信息素选择阈值；ηi,k为启发值；τi,k为信息素；β为启发值重要程度因子，其值越大，表示启发值在转移过程中的作用越大。J的计算方法为：首先计算当前Maklink线上的节点i到下一条Maklink线j的选择概率Pi,j;然后采用轮盘赌法[10]选取下一个节点。Pi,j的计算式为

(9)

3.2.3信息素的更新原则

信息素的更新包括信息素的实时更新和信息素的路径更新，其中实时更新为每只蚂蚁在选择节点后都需对该节点的信息素进行更新，更新公式为

τi,j=(1-ρ)τi,j+τ0ρ

(10)

式(10)中:τ0为信息素的初始值；ρ为[0,1]内的可调参数，表示信息素的挥发程度。

在第1次迭代完成之后，所有蚂蚁走完从点S到点T的路径，从中选取距离最短的一条，更新该路径上所有点的信息素,更新公式为

(11)

式(11)中:L*为所选择路径的长度；ρ为[0,1]内的可调参数，表示信息素的挥发程度。

3.3路径调整

应用蚁群算法优化之后，可得到一条基于Maklink图的最短路径，该路径可满足式(1)、式(2)及式(4)的约束，但由于Maklink线的缘故，该优化后的航线通过几条Maklink线就有几个转向点，并不能满足航海中转向点的设置应尽可能少的实际需求。同时，未必能满足式(3)的约束。因此，需对优化后的路径作进一步的调整，从而满足上述要求。

调整的思路为:取优化后的路径点，采用回溯的方式，按照从终点T到起点S的方向，将获得的路径点回溯一遍，在保证点与点之间相连的线段不穿过障碍物的前提下，尽可能地裁弯取直，这样既可减少转向点，又能控制转向角度不会过大。具体调整流程[4]见图4。

图4 路径调整流程

4 算法模拟

以从电子海图系统中截取的海图(见图5，其中白色为岛屿)为例，利用MATLAB软件对截图中的障碍物进行凸多边形化，并完成Maklink图构建，构造无线网络图，运用算法得到优化后的路径及转向点。

图5 电子海图截图

图6为利用MATLAB软件对电子海图进行处理得到的模型，其中:S和T分别为需规划航线的起点和终点;黑色多边形为对海图中的岛屿进行扩展后生成的凸多边形。

图6 MATLAB模型

图7为对MATLAB建立的模型进行Maklink图化，其中:虚线为Maklink线;黑实线为相邻Maklink线的中点相连得到的无向网络图。

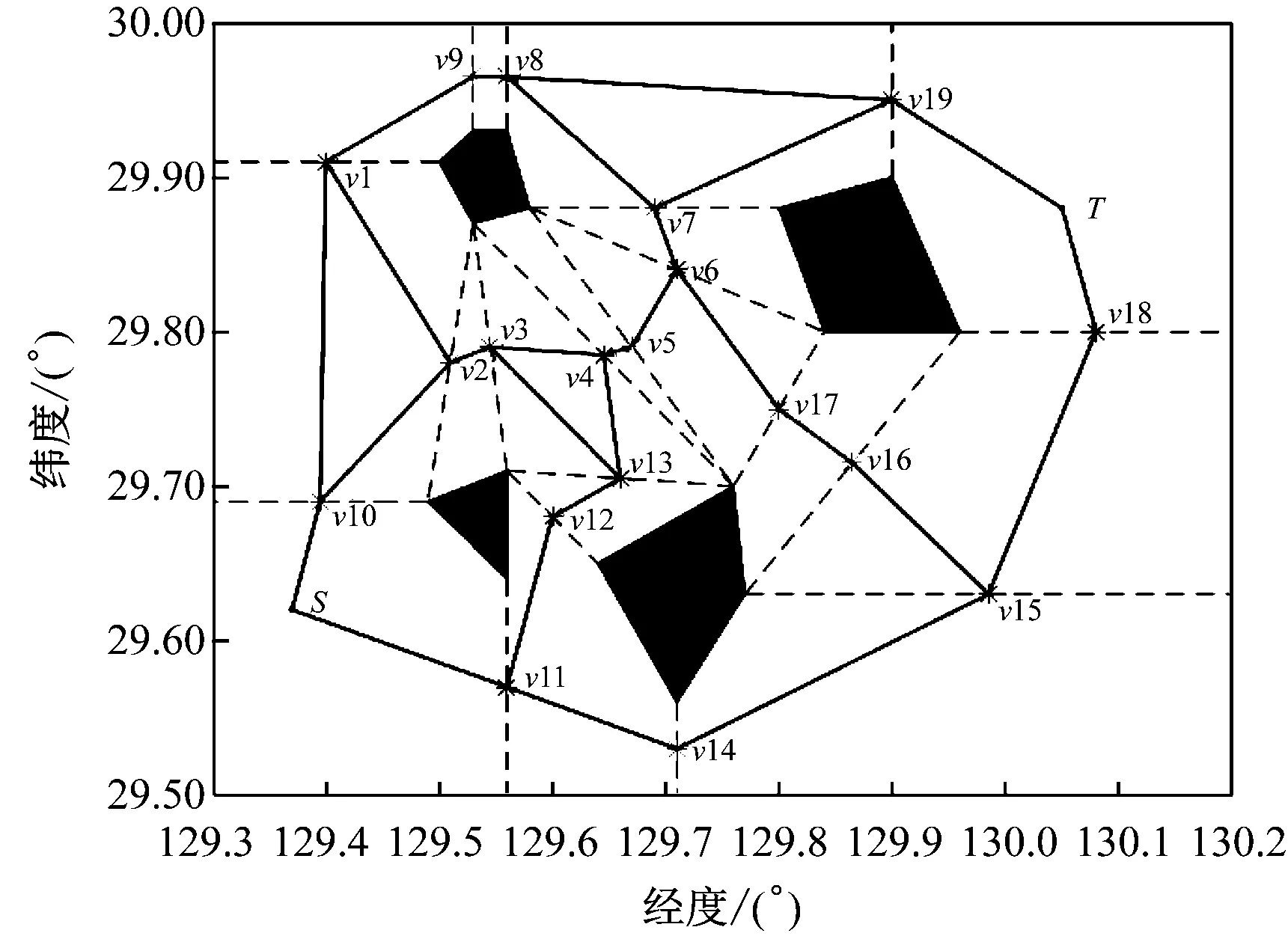
图7 Maklink图和无向网络图

在无向网络图中，首先利用Dijkstra算法规划出次优路径，然后利用蚁群算法对该次优路径进行优化，最后通过裁弯取直过滤掉冗杂的转向点，得到最短路径(见图8)。图8中:黑色粗实线为利用Dijkstra算法得到的次优路径;灰色点划线为利用蚁群算法得到的最优路径;黑色点线为裁弯取直后得到的路线。优化后得到的最优路径转向点分别为:29°52′48″N，129°48′00″E；29°54′36″N，129°54′00″E。该最短航线的长度为40.808 1 n mile。

图8 规划路径图

将利用MATLAB软件模拟得到的转向点输入到电子海图中，最终得到的规划航线见图9。图9中:黑色的实线为航线;点1和点4分别为起点S及终点T;点2和点3为起点与终点间的转向点。

图9 航线生成示例

5 结束语

本文依次从场景建模、航路初始规划和航路优化及调整等3个阶段进行船舶航线规划研究。首先对获取的海图信息进行建模，生成含有安全区的凸多边形;其次利用Maklink图和Dijkstra算法获得初始规划路径;随后采取蚁群算法对路径进行进一步优化;最后在蚁群算法的基础上对已优化航路进行

调整，裁弯取直，删除冗杂转向点，从而满足约束条件。

由仿真试验可知，本文采取的方法可快速实现航线规划，生成可行航线，并能满足转向点角度及转向点数量等方面的要求。与传统的手动进行航线规划相比，本文采用的航线规划方法不仅能减轻船员的劳动强度，而且能考虑多方面因素，避免手动规划航线时可能产生的考虑不周的问题。但是,本文仅研究海图中存在的固定障碍区及危险区，并未考虑周边船舶及天气的影响，这些因素将在今后作进一步的研究。

[1] 张立华,朱庆,刘雁春,等. 电子海图平台下的航线自动设计方法[J]. 大连海事大学学报,2007,33(3):109-112.

[2] 贾传荧,史国友,贾银山,等. 基于电子海图的船舶动态监控系统设计与实现[J]. 大连海事大学学报,2002,28(3):20-22.

[3] 胡江强,曹玉墀,李国帅,等. 谈ECDIS中的安全等深线问题[J]. 世界海运,2016(2):29-32.

[4] 王飞,王红勇. 基于Maklink图和遗传算法的改航路径规划方法研究[J]. 交通运输系统工程与信息,2014,14(5):154-160.

[5] 朱青. 基于蚁群算法的船舶航线设计方法的研究[D].哈尔滨:哈尔滨工程大学,2011.

[6] HABIB M K, ASAMA H. Efficient Method to Generate Collision Free Paths for an Autonomous Mobile Robot Based on New Free Space Structuring Approach[C]// IEEE/RSJ International Workshop on Intelligent Robots and Systems 91 Intelligence for Mechanical Systems, Proceedings, 1991:563-567.

[7] 吴文周,李利番,王结臣. 平面点集凸包Graham算法的改进[J]. 测绘科学,2010,35(6):123-125.

[8] 刘建美,马寿峰,马帅奇. 基于改进的Dijkstra算法的动态最短路计算方法[J]. 系统工程理论与实践,2011,31(6):1153-1157.

[9] HLAING Z C S S, KHINE M A. Solving Traveling Salesman Problem by Using Improved Ant Colony Optimization Algorithm[J]. International Journal of Information and Education Technology,2011,1(5):404-409.

[10] 李永林,叶春明,刘长平. 轮盘赌选择自适应和声搜索算法[J]. 计算机应用研究,2014,31(6):1665-1668.

NavigationRoutePlanningwithMaklinkGraphandAntColonyAlgorithm

CHENXiao,DAIRan,CHENChangyuan

(School of Navigation, Dalian Maritime University, Dalian 116026, China)

An automatic method to optimize ship routeing is proposed. The practical details which should be taken into consideration in navigation route planning are analyzed. The programming model for minimizing total route length under constraints is developed which takes obstacle areas, dangerous areas and the limitations in the turning angle and turning point number into account. The Maklink graph and Dijkstra algorithm are used to establish the preliminary route scheme. The ant colony algorithm is applied to optimize the route. The as-short-as possible route is obtained after further adjustment according to the constraints. The test results demonstrate that the proposed method has considerable advantages over traditional methods and electronic chart methods in terms of efficiency, fuel consumption and safety.

ship engineering; an automatic method； Maklink graph； Dijkstra algorithm； ant colony algorithm

U692.3+1

A