应用型人才培养模式下《复变函数》课程可视化教学实现
王日栋,汤 获,李书海,敖 恩,周海燕,刘春辉
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
应用型人才培养模式下《复变函数》课程可视化教学实现
王日栋,汤 获,李书海,敖 恩,周海燕,刘春辉
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
《复变函数》是数学与应用数学专业的一门重要基础课,其在讲授和理解上都很困难.本文基于MATLAB的工具包,将某些初等函数图像具体化,同时对留数与积分计算也进行了简单探讨,有助于学生对本课程的理解和掌握,也能够提升学生的学习兴趣.
复变函数;可视化;MATLAB;教学
《复变函数》是数学与应用数学专业的基础课程,也是物理、电子、地质等多个学科的重要专业课程.复变函数就是自变量为复数的函数,在某种意义下可导的复变函数称为解析函数[1].复变函数的自变量和因变量都是复数,它在某些方面有着与实变函数截然不同的特征,如负数可以开偶次方及计算对数,对数函数和根式函数都是多值函数,正弦函数和余弦函数的模不但可以大于1,而且是无界的等,这使得复变函数在教师讲授和学生理解上都很困难,因此,我们需要借助函数的图像来帮助我们理解.由于复变函数的实部和虚部为二元实函数,所以需要在四维空间中描绘其图像.MATLAB作为强大的数学辅助工具可以很好地实现.若用x轴和y轴分别表示自变量的实部和虚部,用z轴表示因变量的实部,就能刻画三维空间图像;若再用曲面的颜色代表因变量的虚部,这样就能刻画四维空间图像.
1 函数图像的描绘
在MATLAB2014中,我们可以用简单的命令来画出基本初等函数的图像,以描绘指数函数图像的M文件为例:
x=[-4*pi:pi/15:4*pi];
[x,y]=meshgrid(x);
z=x+i*y;
u=exp(z);
surf(x,y,real(u),imag(u));
hold on;
colorbar('vert');
title('u=exp(z)').
描绘不同的函数图像时只需要将语句u=exp(z)转换成相应的函数语句即可,如正、余弦函数分别可以写成u=sin(z)、u=cos(z).
1.1 单值复变函数—正弦、余弦函数
对于余弦函数f(z)=cos(z),其代数形式可以表示为:

而正弦函数则可以表示为:

图1和图2分别表示半径为5的余弦函数图像以及其实部图像.图3和图4分别表示半径为5的正弦函数图像及其实部图像.从解析表达式上可知余弦(正弦)函数为单值函数,其实从其图像上也可以看出.从余弦(正弦)函数的解析式以及复数模的计算方法可知余弦函数的模是可以大于1的.

图1 |z|=5时的余弦函数图像

图2 |z|=5时的余弦函数实部图像

图3 |z|=5时的正弦函数图像

图4 |z|=5时的正弦函数实部图像
1.2 多值复变函数—对数函数、根式函数
复数范围内的对数函数log(z)的表达式为:
f(z)=log(z)=log|z|+i(θ+2nπ)(n=0,±1,±2…),其与实数范围内对数函数的差别主要有两点:(1)负数的对数是有意义的,即使虚部为零时,若z=x,当x为负数时,z的对数也是存在的.(2)对数函数是多值函数,其原因是辐角的多值性,这一点从表达式上也可以得到体现.对数函数的实部仍然是单值函数,但其虚部对应于复平面内一点存在无穷多个值,相邻之间相差2π.图5给出的是对数函数log(z)的图像,图6给出的是对数函数log(z)的实部图像,图7显示出的是对数函数log(z)的多值性,我们给出了4个值作为代表.

图5 对数函数的图像

图6 对数函数的实部图像

图7 对数函数的多值性(4个值)


图8 根式函数的图像

图9 根式函数的实部图像

图10 根式函数的图像
其中的θ为辐角主值,从表达式可以看出根式函数的多值性主要是由于辐角的多值性.图8和图9分别给出了根式函数的图像及其实部图像.从图8我们可以看出对于每个自变量,都有两个因变量与其对应;当n=5时,从图10可以看出每个自变量对应5个值.
2 留数与积分计算
2.1 留数计算
复变函数中的留数计算是一个难点,极点的位置不同、阶数不同都影响留数计算.针对极点的不同情况进行分析,应用MATLAB提供不同的计算留数语句及方法来进行处理.将需要计算留数的解析表达式f(z)用f表示,当z0为一阶简单极点时,我们可以用命令R=limit(f*(z-z0),z,z0)来计算,当z0为m阶简单极点时,我们需要将命令语句改写成如下的形式:R=limit(diff(f*(z-z0)^m,z,m-1)/prod(1:m-1),z,z0).如果解析表达式f(z)仅为简单极点的有理函数,我们还可以通过命令[R,P,K]=residue(B,A)来计算,其中向量B为表达式f(z)的分子系数,A为表达式f(z)的分母系数,命令的返回值有三个,分别是留数向量R,极点位置P和表达式f(z)的直接项K.
分析:法一:应用limit命令.
从题知可知,z=1和z=-1分别是函数f(z)的一阶极点和二阶极点,应用MATLAB计算留数时需要用不同的语句.建立M文件如下:
syms z;
f=z/(z-1)/((z+1)^2);
R1=limit(f*(z-1),z,1);
R2=limit(diff(f*(z+1)^2,z,1)/prod(1:1),z,-1),
运行结果为R1=1/4;R2=-1/4,与理论计算结果相同.
法二:应用residue命令.
编写M文件如下:
clear;
syms z;
A=[1,0];
B=[1,1,-1,-1];
[R,P,K]=residue(A,B),
方法二的好处在于一次性可以计算出所有极点及其留数,不用考虑极点的多重性,但其限制也是明显的,只能用于有理表达式中.
分析:此题中函数的分子为指数函数,不能应用residue语句,只能用limit语句,编写M文件,分别计算当z=πi和z=0时的留数,结果如下:
R1=1/(6*pi^2)+i/pi^3-3/pi^4-(4*i)/pi^5;
R2=1/pi^4-(4*i)/pi^5.
2.2 用留数计算积分
计算出函数的留数以后,应用留数定理计算复变函数积分就变得相对简单了.分析所求积分区域内所包含的极点,对每一个极点计算出相应的留数,再用留数定理可得积分结果为S=2πi(sum(R)),sum(R)表示各极点留数的和.
分析:通过分析我们知道该积分具有4个极点:-i,1,3,∞,而在区|z|≤2内只有两个极点-i,1,因此只需要计算出这两个极点的留数,再应用留数定理即可计算出该积分.应用MATLAB编写M文件如下:
clear;
syms z;
f=1/(z+1i)^10/(z-1)/(z-3);
r1=limit(diff(f*(z+1i)^10,z,9)/prod(1:9),z,-1i);
r2=limit(f*(z-1),z,1);
S=2*pi*1i*(r1+r2),
即可计算出积分的值S=pi*(237/312500000+(779*i)/78125000).该积分的理论解为整理后可知其与MATLAB计算出来的结果精度在10-20以上,这个精度对一般工业生产、日常生活已经足够了,故对于MATLAB的计算结果我们认为是可以采用的.
3 辐角的计算
众所周知,复数的辐角具有多值性,这就使得很多复变函数具有多值性,这也是复变函数和实变函数的本质区别之一.如何将初等多值函数分解成单值函数也就成为了复变函数的教学难点之一.为了解决这一难点,我们必须彻底弄清辐角函数.在文献[4][5]中,作者对辐角函数的性质进行了系统的挖掘和总结.
在MATLAB中求辐角的标准函数angle(z),其意义是给出复数z的辐角,但实际上它能显示的是复数z的辐角主值,且是用实数表示的,范围为-π<angle(z)≤π,例如 angle(1+i)、angle(-i)、angle(-1)的运算结果分别为是0.78543.1416(π).
由文献[1]可知,我们可以得到复数在做乘法和除法时的辐角变化过程.由欧拉公式可得,任意复数z=x+yi(x,y∈R)都可以表示成指数形式z=er+iθ=ereiθ,且不难验证
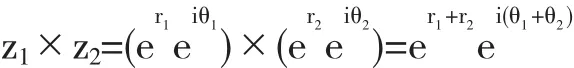
和

成立.从上述公式我们可以看出辐角的变化具有明显的几何意义,即复平面内向量z1和z2的夹角变化,当函数做乘法时为辐角的和,做除法时为分子函数与分母函数的辐角之差.当这个夹角变化不超过主值的规定范围时,我们可以用标准函数angle(z)来计算.
clear;
z1=1+i;
z2=i;
angle(z1/z2);
例5 计算(-1+i)×(-i)的辐角.
4 结论
复变函数作为数学专业的一门重要基础课,学生的学习和掌握程度对其在今后的学习过程中会产生重要影响,因此,我们要做好讲授工作.复变函数的可视化可以将难于理解的知识用四维图像的形式清晰地展现出来.本文利用MATLAB给出了单值的余弦函数图像、多值的对数函数图像,有助于学生能够直观地理解重难点知识.复变函数的可视化不仅有助于学生对书本知识的掌握,也可以提高学生学习的热情,在今后的教学过程中应不断深入研究提高,更好地提高教学质量.
〔1〕钟玉泉.复变函数(第四版)[M].北京:高等教育出版社,2013.
〔2〕徐彬.Matlab在复变函数与积分变换课堂教学中的应用[J].湖北理工学院学报,2016,32(3):68-72.
〔3〕朱建民,李颖.复变函数的可视化问题[J].大学数学,2011,27(1):175-178.
〔4〕金庭枝,王长庆.多值函数的单值解析分析[J].辽宁师范大学学报(自然科学版),2000,23(2):217-219.
〔5〕王金花.一类多值函数的单值解析分支[J].沧州师范学院学报,2016,32(1):17-19.
O174.5-4
A
1673-260X(2017)10-0004-04
2017-08-12
赤峰学院教学改革研究项目(JGXM201617)

