基于折射率匹配方法的球床三维重构

林大富 刘峰瑞 陈兴伟 严睿 梅牡丹 张洁 邹杨



基于折射率匹配方法的球床三维重构

林大富1,2刘峰瑞1,2陈兴伟1严睿1梅牡丹1张洁1邹杨1

1（中国科学院上海应用物理研究所嘉定园区 上海 201800） 2（中国科学院大学 北京 100049）

固态钍基熔盐堆(Thorium-based Molten Salt Reactor with Solid Fuel, TMSR-SF)是第四代核反应堆堆型之一，它融合了高温气冷堆的石墨基质包覆颗粒燃料球技术和熔盐堆的高温熔盐冷却剂技术。堆芯的物理设计和几何设计依赖于燃料球在堆芯中的堆积因子，为研究球床堆堆芯模型内燃料球的堆积三维结构，本文提出基于折射率匹配的方法对球床进行三维重构的方案，并通过初步的模拟实验对程序进行验证，旨在探索该方法在球床三维重构中的可行性。针对三维重构中的一系列关键问题进行阐释，并提出相应的解决方案；同时给出了三维重构方案的完整流程，并计算出了衡量三维重构精确度的度量值：直径重叠量。最后，搭建了一个小型规则排布的球床实验装置，通过折射率匹配技术开展球床可视化实验以探索该方案在球床三维重构中的精确度，并说明该方法的可行性。试验结果表明，颗粒间平均重叠量为1.43 mm，重构精度有待提高，重构方法有待改进。

折射率匹配，图像处理，可视化液体球床，三维重构，规则球床

熔盐堆是第四代核能系统先进高温堆的候选堆型之一[1]。熔盐球床堆堆芯的堆积因子是指燃料球的体积在堆芯内所占的体积分数，包括燃料球在堆芯内的总体积分数和局部体积分数。堆芯堆积因子是反应堆热工和物理分析中的一个很重要的参数。然而，目前针对熔盐堆堆积因子的研究却缺乏有效的手段。

针对高温气冷堆堆芯球床的堆积因子，从20世纪60年代，国际上就开始使用球床凝固的方法着手研究[2]，然而该方法使得小球无法重复利用；从20世纪90年代开始，科学家逐步开始采用X射线断层扫描[3]、g射线扫描[4]、核磁共振[5]等先进的方法对球床进行三维重构，以研究球床的堆积因子，X射线、g射线可以达到极高的空间分辨率，然而也因此导致数据量和计算量都极大；另外设备昂贵的价格和实验人员的安全性也使得该方法的适用性受到限制；核磁共振方法可以达到亚毫米级的扫描精度，然而扫描速度极慢，同时其要求被扫描的物体中含有氢原子。

以上诸种研究主要是针对高温气冷堆等领域的干燥颗粒堆积的堆积因子研究。在熔盐堆中，燃料球颗粒受浮力和液体填充影响，球床结构与干燥堆积有所不同，因此需要开展液态环境中的球床堆积因子研究。

鉴于此，本文提出使用折射率匹配技术(Refractive Index Matched Scanning Technique, RIMS)[6]搭建可视化球床装置，并结合球床的三维重构来研究球床的堆积因子。RIMS的基本原理，是将一组透光性很好的透明小球浸在与小球材料折射率相同的透明溶液（如NaI溶液）中，构建一个几乎完全透明的液体——球床相混和的颗粒悬浊液；接着使用一束激光片光源按照一定间隔照射球床内部并呈现出球床内部各个位置的二维截面图，然后使用高速相机摄取这些二维截面图片，最后使用图片处理的方法从这些照片中提取出每个小球的位置信息。与上述诸种方法相比，基于RIMS的三维重构方法有如下优点：RIMS环境是由透明液体和固态小球构成，符合熔盐堆堆芯液态熔盐和固态燃料相混合的复杂固液环境；在焦距调节准确的情况下，只需摄像机曝光一次，就能清晰地摄取到球床整个实验截面的截面轮廓图；RIMS设备廉价，只需一个服务器、激光束和一台数码相机。目前RIMS的缺陷是匹配液折射率的调节有比较大的限制，暂时还无法应用到实际的大床径比的球床堆堆芯中。所以，目前本课题组搭建了小型的可视化球床装置来验证基于CCD (Charge-coupled Device)拍摄的断面图像结合阈值分割、图像滤波、霍夫(Hough)变换等图片处理方法，实现对小型球床的三维重构，未来的工作之一便是优化折射率的问题，来提高三维重构的规模。

1 研究方法

本文以RIMS为依据搭建可视化球床实验平台，以NaI溶液模拟熔盐堆堆芯中的熔盐，以亚克力(Polymethyl Methacrylate, PMMA)材料的小球模拟堆芯中的颗粒燃料，并以阈值分割、图像滤波、Hough变换等手段，为图片处理的方法对堆芯三维重构。

1.1 基于RIMS搭建可视化球床模型

为搭建可视化的球床模型，使用到的材料或仪器为：PMMA、NaI粉末、YG激光器、片状激光出射头、CCD高速相机、三维相机移动坐标架。RIMS是搭建该实验装置的核心方法。规则球床包括球和球床外容器壁，均由PMMA材料制成。PMMA是一种透明的材料，其折射率为1.4912。用来匹配球床的溶液是由NaI和水配置成的盐溶液。NaI盐溶液是一种无色透明的溶液，通过调节NaI的配比，其折射率可以接近1.4912，并与PMMA材料达到折射率匹配。实验时，将球床模型完全浸没在与其折射率匹配的NaI溶液中，形成一个透明的球床悬浊液。接着使用YG激光器产生激光，用片状激光出射头来将激光转化为片状的光束，并打在球床的截面上，形成清晰的球床的二维截面图像。高速摄像机固定在可以精确控制移动的三维相机移动台架上，由于球床模型和NaI溶液折射率匹配，因而球床截面的二维结构图像可以清晰地投射在高速相机CCD感光片上。为得到球床模型各个不同深度的截面二维图片，将片状激光投射在堆芯球床内的不同深度处，高速相机便可以清晰地采集到球床的不同截面图片。

1.2 图片处理技术

1.2.1 阈值分割

阈值分割[7]的目的是将图像中的内容按照不同的灰度级，分割为数块可以明显区分开来的区域，并将最终的图片转变为仅含有黑白两个灰度级的图片。若原图像素点(,)处的灰度级为(,)，阈值分割后的图像为(,)，为选取的阈值，则：

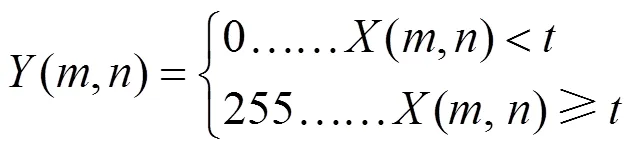
1.2.2 图像滤波

图像滤波[8]旨在尽量保留图像细节特征的条件下对目标图像的高斯噪声和椒盐噪声进行抑制和消除，常用的滤波方法有高斯滤波和中值滤波。

在高斯滤波算法中，图像中每个像素点的灰度级，都由其本身和它邻域窗口内的所有像素值经过以高斯函数为权值进行加权平均而得到。即高斯滤波可以表示为：

式中：W,y表示中心像素(,)的×（为奇数）大小的邻域；ω为空间距离相似度权重因子。

中值滤波算法的核心是将图像中每个像素点的灰度值，设置为该点领域内所有像素点灰度值的中值。其遵循的基本公式如下：

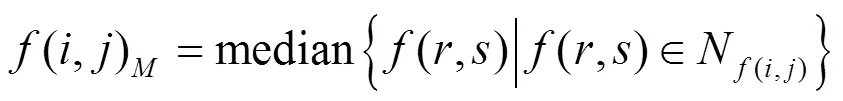
1.2.3 边缘检测

边缘检测[9]的实质是采用算法来提取出图像前景中的对象和背景间的交界线。相对于其他边缘检测算法，Sobel算法检测速度快，对噪声具有平滑和抑制的能力。Sobel算法分别使用水平和垂直方向的窗口算子，结合式(4)、(5)进行卷积运算，并求出梯度值|f|+|f|。

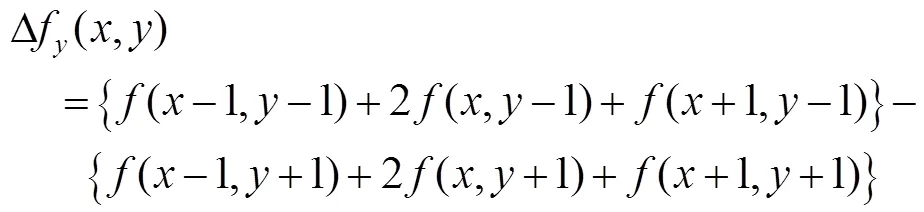
通过设定阈值使图像二值化，梯度值大于等于阈值的点为边缘点，反之则不是边缘点，从而实现边缘检测。

1.2.4 Hough圆变换

Hough变换[10]是一种“投票表决”的算法，其常用来对图像中的直线和圆进行检测，返回直线或圆的圆心。其检测圆的基本思想如下：

1) 利用“圆的任一弦的垂直平分线必通过圆心”这一性质，在图像平面上对于每个前景点(0,0)，在给定的步长上按行（或列）扫描，取该行（或列）上所有前景点(x,y)；

2) 连接、两点，并做直线的垂直平分线；

3) 如果、两点都在圆周上，必经过圆心，与Hough变换相同，将变换平面上每个点作为一个累加器，经过的每个点分别加1，由于噪声点比例毕竟小于有效图形所占比例，因此非圆心点所通过的直线数量会远小于圆心点通过的直线数量，变换结束后寻找各累加器的最大值所在位置便得到该圆的圆心坐标。半径值则存储在另外一个内存空间上，该内存空间上各单元记录该点与点的距离（即半径），找到圆心后，在半径平面上对应位置的值即圆心的半径。

2 数据提取

基于二维图片的三维重构，其首要关键点是从二维图片中提取出三维的坐标点信息。基于球床二维截面图的三维重构，其关键点就是从图片中提取出每个截面圆圆周上数点的三维坐标。而实际情况中，由于受到实验时光照、截面深度、折射率实际匹配度等因素的影响，使得CCD相机最终摄取到的图片质量降低，主要表现为：图片中除了出现小球的截面圆之外，还出现容器的上、下、左、右边界处的壁面；因受壁面强反光，而导致的图片中相应壁面位置亮度过强，进而遮盖住了壁面附近的小球，使得壁面附近小球截面圆受到强光干扰而出现残缺；由于激光亮度的限制，以及光束范围的限制，导致球床下部和背离激光的右侧受光不足，进而使二维截面照片中，相应于球床右侧和下部的截面圆亮度过低，轮廓几不可见；因PMMA材料和NaI折射率匹配的偏差，使得球床中深度较大的截面圆反射到CCD镜头时发生扭曲，照片中的圆亦扭曲。以上诸因素，将直接影响数据能否提取以及提取出数据的准确性。

针对以上问题，本文根据图片处理技术给出相应的解决方案。OpenCV是计算机视觉领域中的一套经典的开源软件[9]。本文借助OpenCV，采用阈值分割、滤波、边缘检测和霍夫圆检测等手段，提高图片质量，突出图片中截面圆的亮度，增强了亮度过低的轮廓，并采用最小外接矩形的方法，提取出圆周扭曲严重的截面圆上的点坐标。

2.1 壁面的消除

由于球床结构的特点，摄取的照片不可避免地会受到球床壁面反射光的干扰。图1为球床中心附近截面处的截面照片。照片中，上壁面面积大，反光能力强，导致照片中的上壁面光线强度大，占据照片中的范围也大。假如不对其进行处理，而是将照片整体进行阈值变换和滤波之后，直接进行霍夫圆检测（图2），将会导致检测结果中误检出许多本没有的截面圆。而本文使用OpenCV工具将壁面的景像擦除，再于阈值变换和滤波之后进行霍夫圆检测（图3），结果显示在壁面处，误检的截面圆大量减少。表明在二维照片中直接擦除壁面的景像，对正确检测出截面圆是有效的。

图1 球床中截面附近位置（z=5 mm处）

图2 阈值分割、中值滤波得到的图片(a)和检测出来的圆形的结果(b)（z=5 mm处）

图3 对壁面景象进行擦除(a)和检测出来的圆形的结果(b)

2.2 边缘修补

由于受激光光强和光束范围的限制，球床下部和右上部受光不足，摄取到的照片中，下方和右上方的圆轮廓光强过低，导致该处的轮廓检测和坐标提取失效（图4）。若是对一张照片整体使用单一阈值进行阈值变换，那将导致局部轮廓提取残缺严重。但若是能够单独截取出这些光强低的部位，使用与之适应的阈值进行阈值变换，就能大大提高轮廓提取质量。本文使用OpenCV工具编写程序，实现局部阈值变换和轮廓增强（图5），之后再进行轮廓圆检测，结果显示残缺的圆被有效检出（图6）。

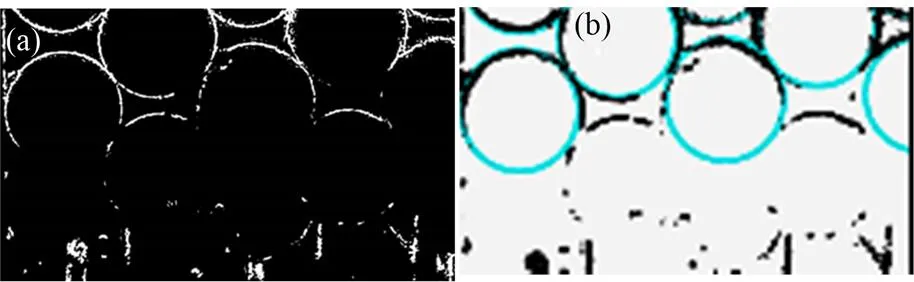
图4 图片下方残缺的轮廓(a)和轮廓残缺处圆形检测失败(b)

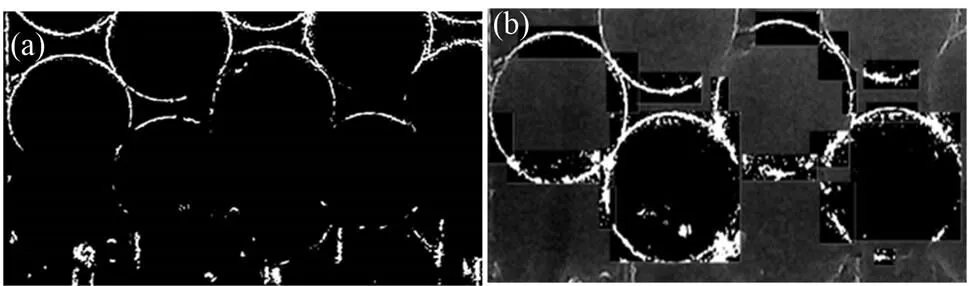
图5 轮廓局部增强前(a)和后(b)

图6 轮廓局部增强前(a)和后(b)的圆形检测对比

2.3 轮廓变形

基于RIMS搭建的可视化球床模型，PMMA材料和NaI溶液的折射率配比程度将会影响相机摄取到的轮廓图片的质量。由于实际折射率匹配过程中，折射率无法达到精确的一致，使得从球床远处截面反射到相机上的过程中，必然导致当激光从深度过大的球床截面反射到相机CCD板上之前，发生过多的偏折散射，致使最终摄取到的截面圆发生扭曲（图7）。

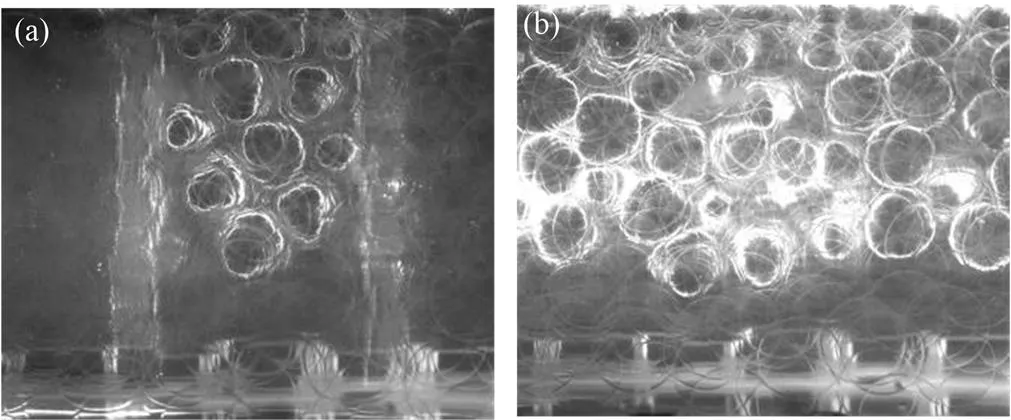
图7 z=−30 cm (a)和z=−20 cm (b)处的球床截面

截面圆的扭曲过大，圆某些部位的轮廓变粗，若是直接在图片进行阈值和滤波变换之后就进行霍夫圆检测，将导致轮廓圆的定位出现较大偏差。如图8中，图8(a)共有8个圆轮廓，图8(b)相应位置检测出的圆轮廓并不与真实轮廓完全重合，如最下面的球，霍夫变换得到的标准圆轮廓并不与原来的轮廓相重合，而是比白色轮廓略大；最左边一个小球的检测结果也是类似。

图8 阈值、滤波处理(a)和霍夫圆检测(b)

针对截面圆变形后，霍夫圆检测不准确的问题，本文提出首先对轮廓进行局部增强，之后使用OpenCV中的cvBoundingRect[9]函数，求取轮廓的最小外接矩形，并定位出圆心的位置，即矩形中心点的位置。如图9所示，是轮廓增强前后的图片，图10是对增强之后的图片求取最小外接矩形。

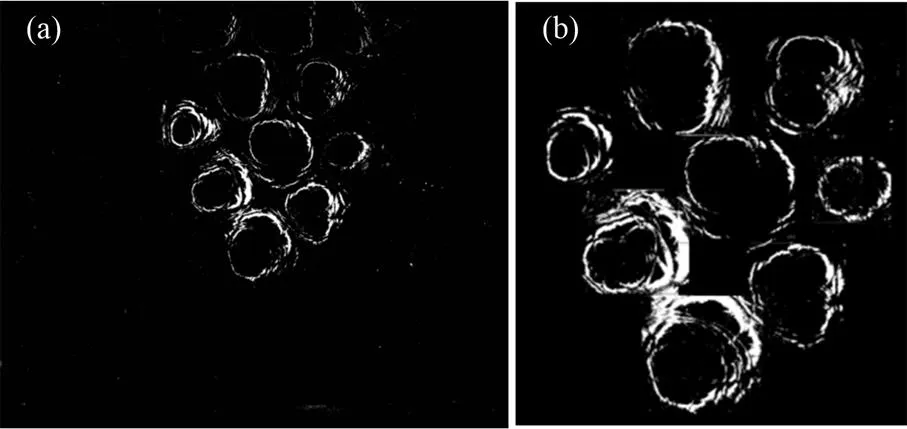
图9 轮廓增强前(a)和后(b)

圆周上数据的提取，需要知道轮廓圆的半径值。由于cvBoundingRect函数得到的是轮廓的外接矩形，不是正方形，因而本文对矩形的长边和短边求取算术平均值作为轮廓圆的直径。

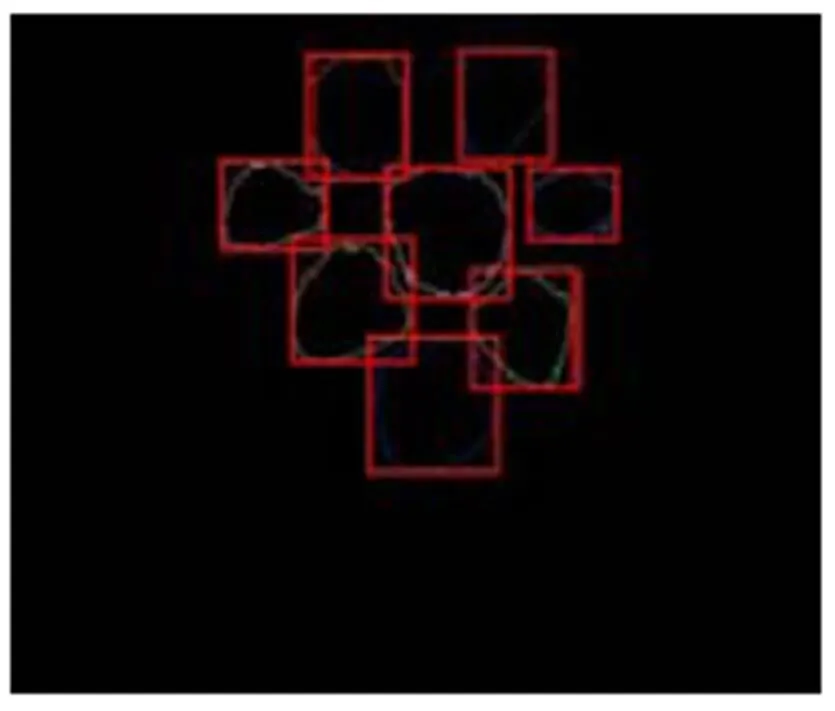
图10 求取最小外接矩形

2.4 三维重构完整步骤

在克服了图片质量低，并成功提取出所有照片中轮廓圆上数点的三维坐标之后，就可以使用MATLAB中的nlinfit函数，进行球形拟合，拟合出球床中所有小球的球心坐标，并画出最终的球床结构三维图。三维重构完整步骤如下：

1) 根据RIMS原理的要求，配置与球折射率匹配的NaI溶液。

2) 保持相机和激光的相对位置固定，按照一定深度间隔拍摄球床完整的截面照片，并记录下每张照片相应于球床的深度。

3) 将一标尺插入溶液中的适当位置，并拍下用于相机标定的照片，从照片中算出照片上单位像素和实际空间长度的转换比例值。

4) 提取出每张照片中每个截面圆上至少10个点的二维像素坐标，将之乘上上一步相机标定时算出的比例值，再结合该照片所处的实际深度值，便可以得到截面圆上点的实际三维坐标。

5) 从提取出来的所有三维点坐标中，归类出属于同一个球面的点，接着使用MATLAB中的nlinfit函数，对归类出的点进行球面拟合，得到球床中所有小球的球心坐标。将坐标系原点从相机光心转移到球床中的某个小球球心上，得到每个小球球心的相对坐标。

6) 计算球床的球径重叠率，评估三维重构的准确性。

3 三维重构验证

为验证本文所提出的三维重构程序，建立了一个按照体心立方排布的规则球床，并对其实施三维重构的完整过程。

3.1 规则球床实际的球心

试验所采用的球床是由414个3 cm直径的PMMA小球按照体心立方规则排列而成。球床总共12层，整体形状和上顶盖形状如图11所示，奇数层和偶数层小球的排列如图12所示。从球床最底部往上，第1、3、5、7、9、11层球，都是按照图12(a)排列，每层32个球，最近邻两个球之间的距离为35 mm；第2、4、6、8、10、12层球的排布，是按照图12(b)所示的规律，每层37个球，最近邻两球之间的间距为35 mm。球床外容器水平截面是一个八边形，长边112 mm，短边82 mm，球床竖直高度为21.65 cm，每层球高度16.956 mm。

图11 规则球床上顶盖形状(a)和整体形状(b)

两层小球的排列情况为如图12所示。

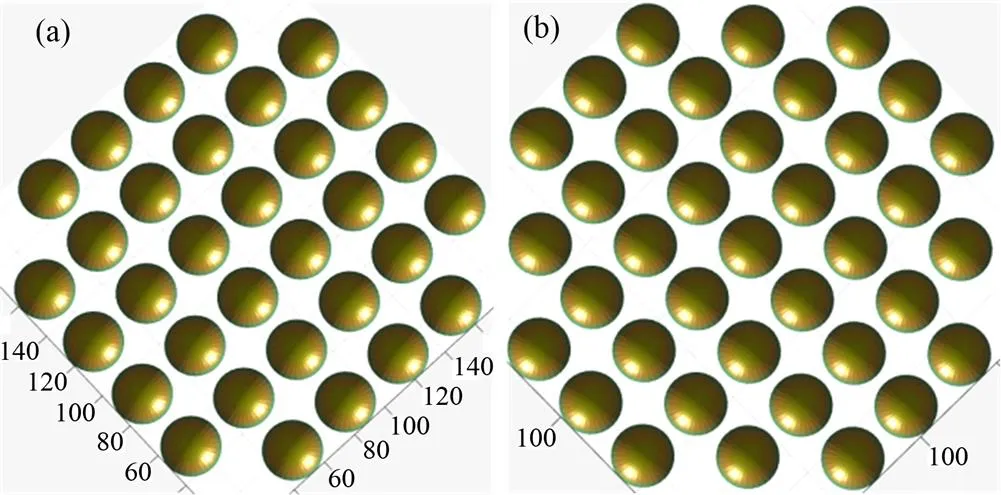
图12 第1、3、5、7、9、11层(a)和第2、4、6、8、10、12层(b)球的排列

3.2 照片摄取

将摄像机和激光片光源固定在三维台架上，并且相机光轴和光源方向相互垂直摆放。考虑到每个小球的直径是30 mm，因而控制片光源每沿着光轴方向前进5 mm拍摄一张照片，这样对于每一个小球，都可以得到5张不同深度的清晰的轮廓照片。拍照从球床离相机最近的一端开始，片光源每向前移动5 mm，就拍摄一张球床截面照片，直到片光源移动到球床离相机最远的一端，拍照停止。于是，便可以得到球床全部的截面图片。

3.3 球床重构及结果

从摄取到照片中提取出点数据，并进行球形拟合，得到球床中所有小球的球心和半径值。根据得到的球心和半径值，利用MATLAB强大的绘图功能画出球床的排列结构。

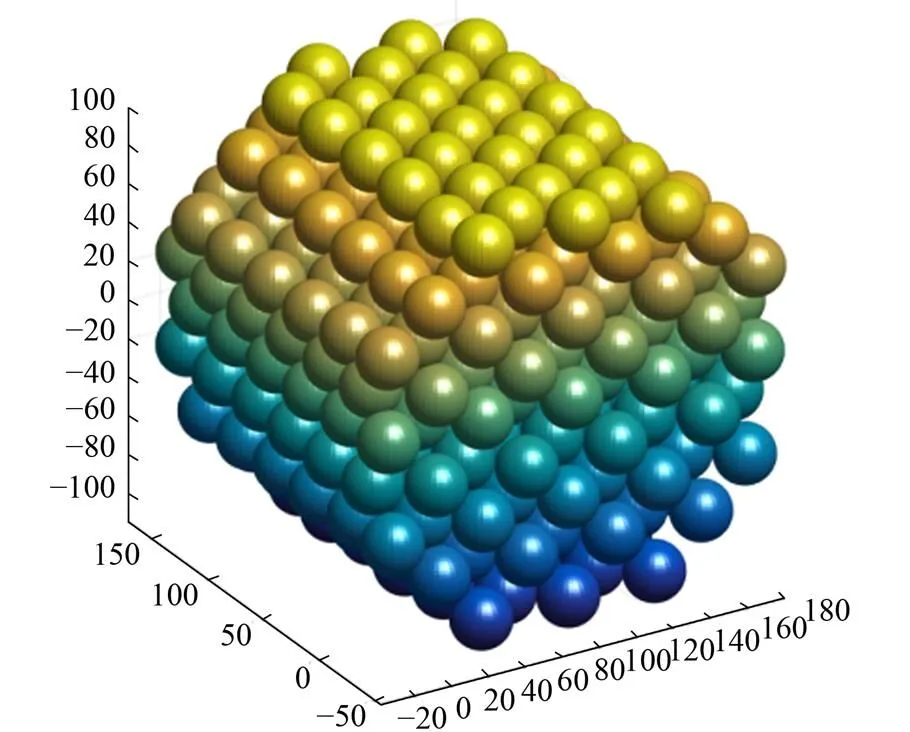
图13 球床三维重构结果

其中，各层小球的重构结果如图14所示。从各层小球重构的结果上来看，每层小球的排布都没有达到实际理想的规则排布，这将导致三维重构产生误差，并出现相邻小球发生重叠的现象，然而实际上，相邻两层小球之间是相切接触。因而本文使用相邻小球之间的直径重叠量来衡量三维重构的误差情况。

3.4 直径重叠量和直径重叠率

在实际的球床中，每相邻小球之间的重合量极小，可以近似认为相切。因此三维重构的结果中，相邻小球之间的重叠量就是衡量三维重构准确度的量度。在三维重构的结果中，假设球床一共有个小球，其中第个小球和与之相邻的第个小球存在重叠，这两个小球之间的重构距离L，那么球和球之间的直径重叠率定义为：

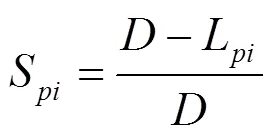
式中：是小球的真实直径。

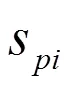
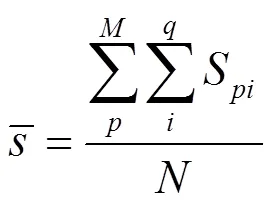
式中：是与小球发生重叠的相邻小球个数。

在本次试验中，真实球床小球之间存在1320次相切接触。在三维重构的结果中发生重叠的次数为852次，每个小球的直径平均重叠率为4.36%，平均重叠量为1.309 mm。本文将852次的重叠情况按照重叠量的多少分为了5类，这5类的分类情况以及具体占比情况如表1所示。

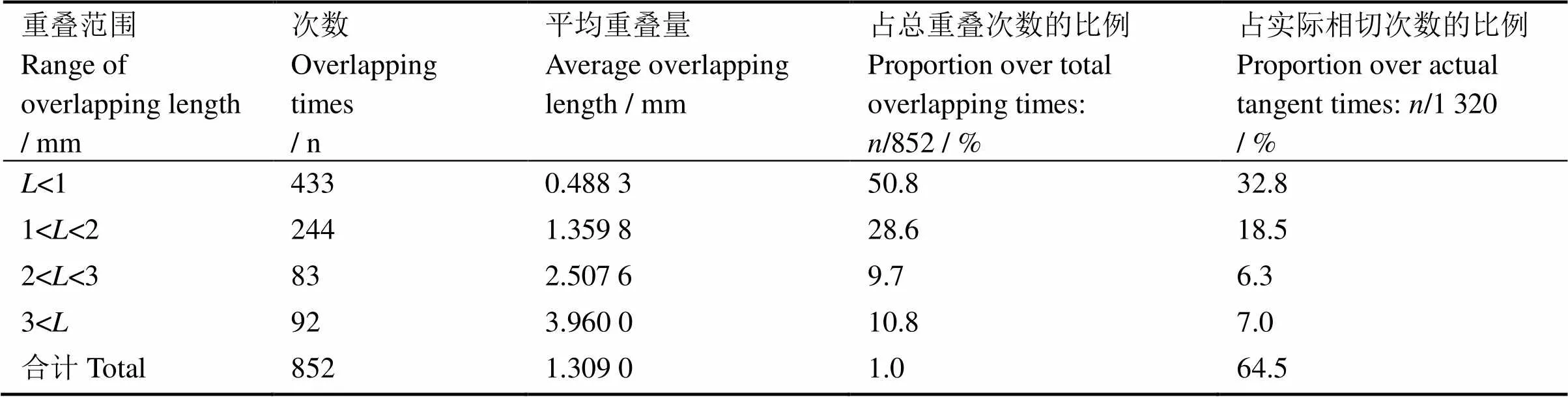
表1 各范围重叠量占比

从表1可见，在实际本该近似为相切接触的接触方式中，有64.5%的比例发生了重叠接触，然而，如果认为重叠量小于2 mm可以接受的话，则大于2 mm的重叠所占的比例为13.3%。

4 结语

由于高温气冷堆堆芯堆积因子研究的手段尚不能完全适用于熔盐堆的堆积因子研究，且目前在熔盐堆堆芯堆积因子的研究方面手段尚且缺乏，本课题组尝试使用折射率匹配结合三维重构的手段来研究这项技术在重构球床内颗粒位置的可行性。本文针对可视化球床装置的三维重构方法进行研究，使用了阈值分割、图像滤波、Hough变换等图片处理方法，虽然实现了球床的三维重构和每个小球的球心定位，然而重构的误差却有待提高，仅有68.2%的比例不发生重叠或重叠率低于1 mm。可见本文提出的针对球床堆芯的三维重构方法有待改进。

1 David LeBlanc.Molten salt reactors: a new beginning for an old idea[J].Nuclear Engineering and Design, 2010, 240: 1644−1656.

2 Benenati R, Brosilow C B. Void fraction distribution in beds of spheres[J]. Aiche Journal, 1962, 8(3): 359−361.DOI: 10.1002/aic.690080319.

3 Mueller G. Radial porosity in packed beds of spheres[J]. Powder Technology, 2010, 203(3): 626−633. DOI: 10.1016/j.powtec.2010.07.007.

4 Auwerda G J, Kloosterman J, Lathouwers D,. Macroscopic and microscopic packing properties of experimental and computational pebble beds[J]. Nuclear Technology, 2013, 183(3): 272−286.

5 Nguyen N L, Van Buren V, Von Garnier A,. Application of magnetic resonance imaging (MRI) for investigation of fluid dynamics in trickle bed reactors and of droplet separation kinetics in packed beds[J]. Chemical Engineering Science, 2005, 60(22): 6289−6297.DOI: 10.1016/j.ces.2005.04.083.

6 Wiederseiner S, Andreini N, Epely-Chauvin G,. Refractive-index and density matching in concentrated particle suspensions: a review[J]. Experiments in Fluids, 2011, 50(5): 1183−1206.DOI: 10.1007/s00348-010-0996 -8.

7 艾淑芳, 闫钧华, 李大雷, 等. 遥感图像中的机场跑道检测算法[J]. 电光与控制, 2017, 24(2): 43−46.DOI: 10.3969/j.issn.1671-637X.017.0.009. AI Shufang, YAN Junhua, LI Dalei,. An algorithm for detecting the airport runway in remote sensing image[J]. Electronics Optics & Control, 2017, 24(2): 43−46. DOI: 10.3969/j.issn.1671-637X.017.0.009.

8 雷浩鹏. 数字图像去噪算法研究及应用[D]. 长沙: 长沙理工大学, 2010. DOI: 10.7666/d.Y1699449. LEI Haopeng. The research and application of digital image de-noising algorithm[D]. Changsha: Changsha University of Science & Technology, 2010. DOI: 10.7666/d.Y1699449.

9 于仕琪, 刘瑞祯. 学习OpenCV[M]. 北京: 清华大学出版社, 2009.YU Shiqi, LIU Ruizhen. Learning OpenCV[M]. Beijing: Tstinghua University Press, 2009.

10 杨治明, 周齐国. 基于霍夫变换理论的图形识别[J]. 重庆工业高等专科学校学报, 2002, 17(4): 16−17.DOI: 10.3969/j.issn.1673-1999.2002.04.005. YANG Zhiming, ZHOU Qiguo. The recognition of the geometric figure based on the Hough transformation theory[J]. Journal of Chongqing Polytechnic College, 2002, 17(4): 16−17. DOI:10.3969/j.issn.1673-1999. 2002.04.005.

A 3D-reconstruction research on the visual liquid-pebble bed

LIN Dafu1,2LIU Fengrui1,2CHEN Xingwei1YAN Rui1MEI Mudan1ZHANG Jie1ZOU Yang1

1(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China)2(University of Chinese Academy of Sciences, Beijing 100049, China)

Thorium-based molten salt reactor with solid fuel (TMSR-SF) is one type of the fourth nuclear power plant which combines high-temperature graphite-matrix coated-particle pebble fuel for high- temperature gas-cooled reactors and liquid salts developed for the molten salt reactors. The design of TMSR-SF requires detailed understanding of the packing structure of the pebble bed in reactor core.This article is aimed to explore the effectiveness of refractive index matched scanning technique (RIMS) in the 3D-reconstruction of reactor core.The cross sections of the pebble bed are imaged by a charge-coupled device (CCD), then the threshold transformation, filter transformation and Hough transformation are used to process the images, and the coordinates of points on the spheres’ edge are extracted. Then an algorithm is used to acquire the relative center coordinates of each sphere.The result shows that excluding irrelevant distractors can improve the accuracy of the 3D-reconstruction, and creating region of interest (ROI) to make threshold transformation is a good method to enhance circles’ edges, and when the circles in the images distort, minimum bounding rectangle (MBR) functions is more effective than Hough circle transformation.Our scheme of reconstruction can reconstruct the 3D packing structure of the pebble bed with themean distance-overlapped which is 1.43 mm, and this precision needs to be improved later.

RIMS, Image processing, Visual liquid-pebble bed, 3D-reconstrution, Regularly arranged pebble bed

LIN Dafu, male, born in 1992, graduated from Northwest University in 2015, master student, focusing on reactor thermal-hydraulics

ZOU Yang, E-mail: zouyang@sinap.ac.cn

2017-06-01, accepted date: 2017-07-14

TL99

10.11889/j.0253-3219.2017.hjs.40.100606

林大富，男，1992年出生，2015年毕业于西北大学，现为硕士研究生，研究领域为反应堆热工水力学

邹杨，E-mail: zouyang@sinap.ac.cn

2017-06-01，

2017-07-14

Supported by Strategic Priority Research Program of Chinese Academy of Sciences (No.XDA02001002), the Frontier Science Key Program of Chinese Academy of Sciences (No.QYZDY-SSW-JSC016)

中国科学院战略性先导科技专项(No.XDA02001002)、中国科学院前沿科学重点研究项目(No.QYZDY-SSW-JSC016)资助