球形燃料元件中包覆颗粒的分布效应研究

冀锐敏 严睿 李晓晓 戴叶 刘桂民 邹杨



球形燃料元件中包覆颗粒的分布效应研究

冀锐敏1,2严睿1李晓晓1戴叶1刘桂民1邹杨1

1（中国科学院上海应用物理研究所嘉定园区 上海201800） 2（中国科学院大学 北京 100049）

在球形燃料元件中，包覆颗粒的填充因子低于10%，分布具有很大的随机性。本文利用MATLAB程序实现了4种填充的建模方式，即体积等效规则填充、扰动的规则填充、随机的规则填充和完全随机填充模拟燃料球中包覆颗粒的分布。基于固态燃料钍基熔盐堆(Thorium-based Molten Salt Reactor with Solid Fuel, TMSR-SF1)设计中选用的包覆颗粒燃料参数，使用蒙特卡罗程序MCNP6 1.0和ENDF/B VII.0数据库进行了全反射边界条件下的单燃料球临界计算，精确量化了不同的建模方式引起的中子物理特性参数的差异。计算表明，这4种建模方式形成了不同的包覆颗粒聚集程度。包覆颗粒的聚集会导致丹可夫效应的增强，从而增大了中子被燃料吸收的概率，无限增殖因数随之增大，燃料温度系数随之减小。

包覆颗粒燃料，无限增殖因数，温度系数

包覆颗粒燃料球具有失效温度高、支持在线换料等特点[1−3]，已经在高温气冷堆(High-temperature Reactors, HTRs)中得到应用验证。氟盐冷却高温堆(Fluoride-salt-cooled High-temperature Reactors, FHRs)设计中也将包覆颗粒燃料球作为燃料元件的一种主要选项，以达到高安全性和较好的经济性。燃料球中容纳了数以万计的包覆颗粒，这些颗粒的分布具有随机性。这种随机分布对燃料球的中子物理性质具有一定影响。在堆芯物理计算分析中，由于蒙特卡罗程序对栅元、曲面编号数量都有一定的限制，因此研究中常更关注燃料球的随机堆积，对燃料球内的包覆颗粒常选用体积等效规则填充的方式简化处理[4−7]。然而，这种建模处理方式并不能保证燃料区域内包覆颗粒的完整性，不同位置的燃料球中的包覆颗粒的装载量不一致，有一定的差异，因此需要进一步实现包覆颗粒的随机分布模拟，以逼近燃料元件的真实情况。近年来，为了实现这一功能，MCNP (Monte Carlo N Particle Transport Code)等蒙特卡罗程序增加了栅元位置随机扰动的功 能[8−9]，但不支持画图功能，用户需谨慎使用。单球模型的计算表明这种扰动对反应性的影响较小，为10−5量级[5,9]，有待其他方法的对比或验证。

中国科学院“未来先进核裂变能——钍基熔盐堆核能系统”战略先导专项之中的固态燃料钍基熔盐堆(Thorium-based Molten Salt Reactor with Solid Fuel, TMSR-SF1)设计中也采用球型燃料元件，相应的研究工作主要采取规则分布[10−12]。为了实现包覆燃料颗粒随机分布的建模功能，更好地模拟燃料球的实际情况，并研究包覆颗粒不同的分布对中子学特性的影响，本文利用MATLAB程序实现了体积等效规则填充、扰动的规则填充、随机的规则填充和完全随机填充这4种填充的建模方式。并以TMSR-SF1的球型燃料元件为分析基准，开展了不同包覆颗粒燃料分布形式下的中子输运计算，分析了包覆颗粒燃料的分布对关键物理参数，如无限增殖因数、燃料的温度反应性系数等的影响。

1 计算模型与程序介绍

1.1 燃料球结构

球形燃料元件是采用准等静压机械法制备，即将包覆颗粒与石墨粉混合，然后装入模具压制而 成[13]。通过X 线无损检测实时成像技术测试方法，结合X 线计算机断层扫描(Computed Tomography, CT)重建软件可以快速重建出三维断层图像，球形燃料元件内的颗粒分布如图1所示。

图1 球形燃料元件内包覆燃料颗粒空间分布示意图

TMSR-SF1设计中所用的球形燃料元件的基本参数见表1。燃料球由中心燃料填充区域和外部石墨壳组成。燃料填充区域内由约11669个包覆燃料颗粒和石墨基体混合而成。包覆燃料颗粒由UO2核心和4层包覆层组成。

表1 TMSR-SF1球形燃料元件的参数

1.2 计算模型

球形燃料元件的结构具有双重非均匀性，包覆颗粒与燃料区内的基体构成一重非均匀性，燃料区和石墨壳构成另一重非均匀性。这种双重非均匀性增加了中子物理计算的难度。但由于蒙特卡罗程序可以处理任意三维复杂几何结构，可以通过精细的计算模型结合连续截面数据，对各种物理过程提供细致的处理，因此双重非均匀性得到很好的解决。

本文以全反射边界条件的球形燃料元件为计算模型。建立模型的核心工作是使用MATLAB程序基于规则填充和随机填充来模拟包覆颗粒在燃料填充区域的分布。根据TMSR-SF1的设计参数和ENDF/B-VII数据库提供的温度点，计算中石墨散射截面温度选择1000 K，其他所有截面温度选择900 K。

1.2.1 填充方式研究

首先详细描述包覆颗粒燃料的5层结构，然后用MCNP中重复几何结构选项描述包覆燃料颗粒在燃料球内的分布。选用简单立方体栅元(SimpleCubic, SC)规则地填充燃料区域，又称为规则分布模型。规则分布模型进一步细分为以下三种：

1) 体积等效规则填充

通过体积等效方法计算得到简单立方体的边长，因此包覆颗粒燃料的填充是规则的，并且燃料填充区域的边界处存在包覆颗粒被切割的情况。根据燃料球参数，计算可得简立方体的边长约为0.178cm。此种填充方式的示意图见图2(a)。

2) 扰动的规则填充

为了满足包覆颗粒填充的随机特性，在规则填充的基础上，对包覆颗粒的位置增加有限的扰动。MCNP中的URAN卡可以实现这个功能，但扰动程度仍然受限于立方体栅格。扰动原理及其参数设置见式(1)，其中：1、2和3是(0, 1)之间的随机数；δ、δ和δ为用户输入的最大扰动量。此种填充方式的示意图见图2(b)。

这一随机扰动功能仅在计算中开启，画图功能并不支持。为避免包覆颗粒在边界处的切割情况，并且得到最大程度的扰动，缩小立方体边长至0.170cm，燃料填充区域内精确填充包覆颗粒11669个，其余区域直接填充石墨基体。

3) 随机的规则填充

为扩大填充的随机性，进一步缩小立方体边长，将燃料填充区域划分成更多的小区域，然后通过程序随机选择填充包覆颗粒或者石墨基体，以保证包覆颗粒的完整性和填充数目。包覆颗粒的直径为0.092 cm，为达到最大程度的随机性，选择立方体边长为0.093 cm，燃料填充区域内能完整填充包覆颗粒的立方体区域有76759个，通过程序选择将其中的11669个填充包覆颗粒，其余直接填充石墨基体。此种填充方式如图2(c)所示。

4) 完全随机填充

通过MATLAB程序随机产生包覆颗粒位置，保证包覆颗粒燃料之间不会发生重叠，也不会与石墨壳边界相切。在MCNP建模中，逐一定义每个包覆颗粒燃料，随后定义石墨基体。因为MCNP程序中栅元的描述字数有一定的限制，因此需燃料区域划分为多个区域分别进行表述。完全随机填充方式如图2(d)所示。

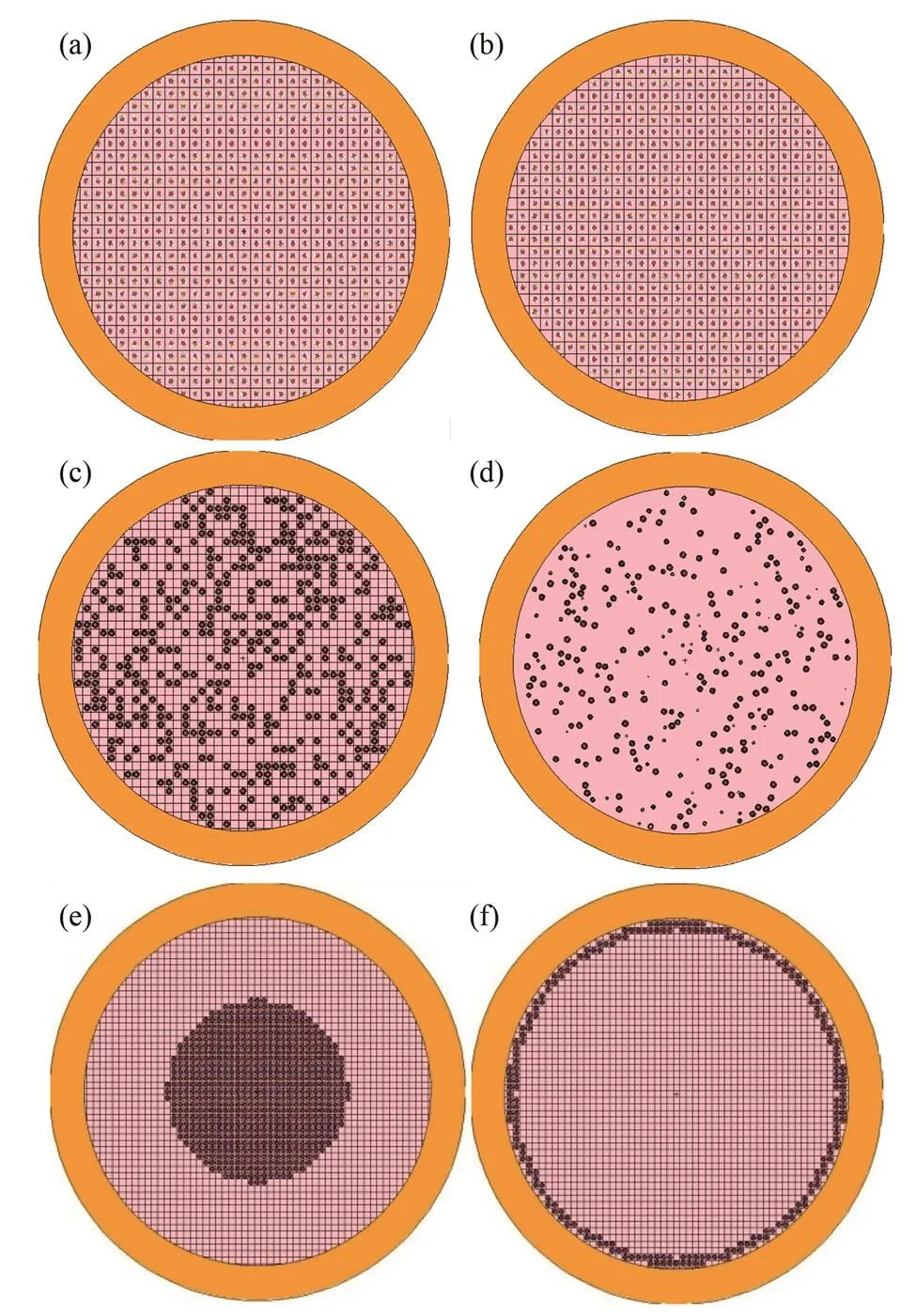
图2 多种填充方式示意图 (a) 体积等效规则填充，(b) 扰动的规则填充，(c) 随机的规则填充，(d) 完全随机填充，(e) 向燃料球心集中，(f) 向燃料球壳集中

1.2.2 规律填充的研究

为研究包覆颗粒不同填充方式的影响，在规则填充的基础上，通过MATLAB程序完成包覆颗粒有规律的填充。本文选取了集中于球心和球壳的两种填充规律，分别见图2(e)和(f)。

1.3 程序介绍

MCNP程序是由美国洛斯阿拉莫斯国家实验室(Los Alamos National Laboratory, LANL)开发的采用蒙特卡罗方法进行输运计算的大型计算机程序[8]。它能够处理中子、电子和光子在各种介质中的运动并给出相应的结果，因此在反应堆物理、辐射防护、核探测等多方面得到了广泛的应用。MCNP程序输入灵活，能够完整地、详尽地在几何结构和材料等方面描述出模型细节；可以选择使用国际、国内数据库资源；程序输出丰富，用户可以根据需求编制输出卡，提取有实际物理意义的多种参数，如有效增殖系数、能谱、单群或多群截面、中子产生和泄漏率等。计算中选用的MCNP版本为MCNP6 1.0，数据库为ENDF/B-VII.0。

2 结果与讨论

2.1 随机填充方式的研究

对图2中的(a)−(d)填充方式均做50组不同的输入，分别计算无限增殖因数∞和燃料温度系数F。计算燃料温度系数时，假设燃料温度上升至1200K。为保证计算精度，临界计算中投入的每代粒子数为105，有效循环次数为103，单次临界计算的标准差约0.00007。

1) 体积等效规则填充

首先完成包覆颗粒的建模，随后将其放入简单立方体内，把这一结构设置为无限重复栅元，在保持无限栅格的前提下，移动燃料球的位置，变化边界条件，达到不同的切割效应。根据体积等效原则，50次燃料球随机定位的情况中最少装载约11637个包覆颗粒(−2.79‰)，最多装载约11684个包覆颗粒燃料(+1.30‰)，平均少装载3.5个包覆颗粒燃料(−0.29‰)。

2) 扰动的规则填充

50次扰动统计结果为：包覆颗粒距离燃料球心的平均距离(o)为1.8358 cm。

3) 随机的规则填充

50次不同的填充统计结果为：包覆颗粒距离燃料球心的o为1.8408 cm。

4) 完全随机填充

经统计，50次不同的填充情况中，包覆颗粒距离燃料球心的o为1.8454 cm。

4种填充方式的计算结果统计见表2。4种不同的填充方式，共200次的计算结果统计表明，平均无限增殖因数∞平均值为1.54738，最大和最小平均无限介质增殖因数∞之间相差(Δ)为7.37×10−3，平均燃料温度系数F为−2.616×10−5K−1。

表2 4种填充方式结果统计

对于以上计算结果进一步采用MATLAB中的箱线图进行统计，见图3。图3(a)−(d)中的横坐标分别对应于图2中的填充方式。箱线图中从下往上的4个横线显示了数据的5个特征值，下内限值、下四分位数(1)、中值(Medium)、上四分位数(3)和上内限值。箱内含有50%的值。下内限值的定义为下四分位数(1)减1.5倍的上下四分位数的差值(R=3−1)。上内限值的定义为3加1.5倍的R。上下内限之外的值以“+”表示，称之为异常值。内箱线图可以粗略估计数据是否具有对称性，粗略观察数据的分散程度。由图3(a)可见，∞数据R为0.0005，中值在箱的下端，可见数据对称性较差，并且数据分布较为分散；图3(b)中∞数据R为0.0001，中值在箱的中端，可见数据分布较为集中且对称性较好；图3(c)中∞数据R为0.0002，中值在箱的下端，数据的对称性较差，数据分布较为集中，但数据中存在少量的异常值；图3(d)中∞数据R为0.0002，中值在箱的中间，数据有较好的对称性，数据分布也较为集中。

2.2 规律填充的研究

2.2.1 集中于球壳

在集中于球壳规则填充的基础上，通过改变立方体栅元的长度，改变包覆颗粒之间的平均距离，计算结果见表3。其中：为简立方体长度；o为包覆颗粒到燃料球心的平均距离；2为包覆颗粒间的平均距离；G为石墨温度系数。随着填充栅元的逐步变大，∞逐渐从1.56261增加至1.54595，相差1.666×10−2，燃料温度系数逐渐从−2.459×10−5K−1增加至−2.634×10−5K−1，变化了8%。

为分析这一变化原因，根据定义分别计算了4因子：快中子增殖因数、逃脱俘获共振因数、热中子利用系数和有效裂变中子数。随着包覆颗粒之间平均距离的接近，空间自屏效应发生了变化，燃料核吸收共振中子的能力减弱，增加约1.4%，而降低约1.3‰，降低约0.04‰，降低约0.01‰。

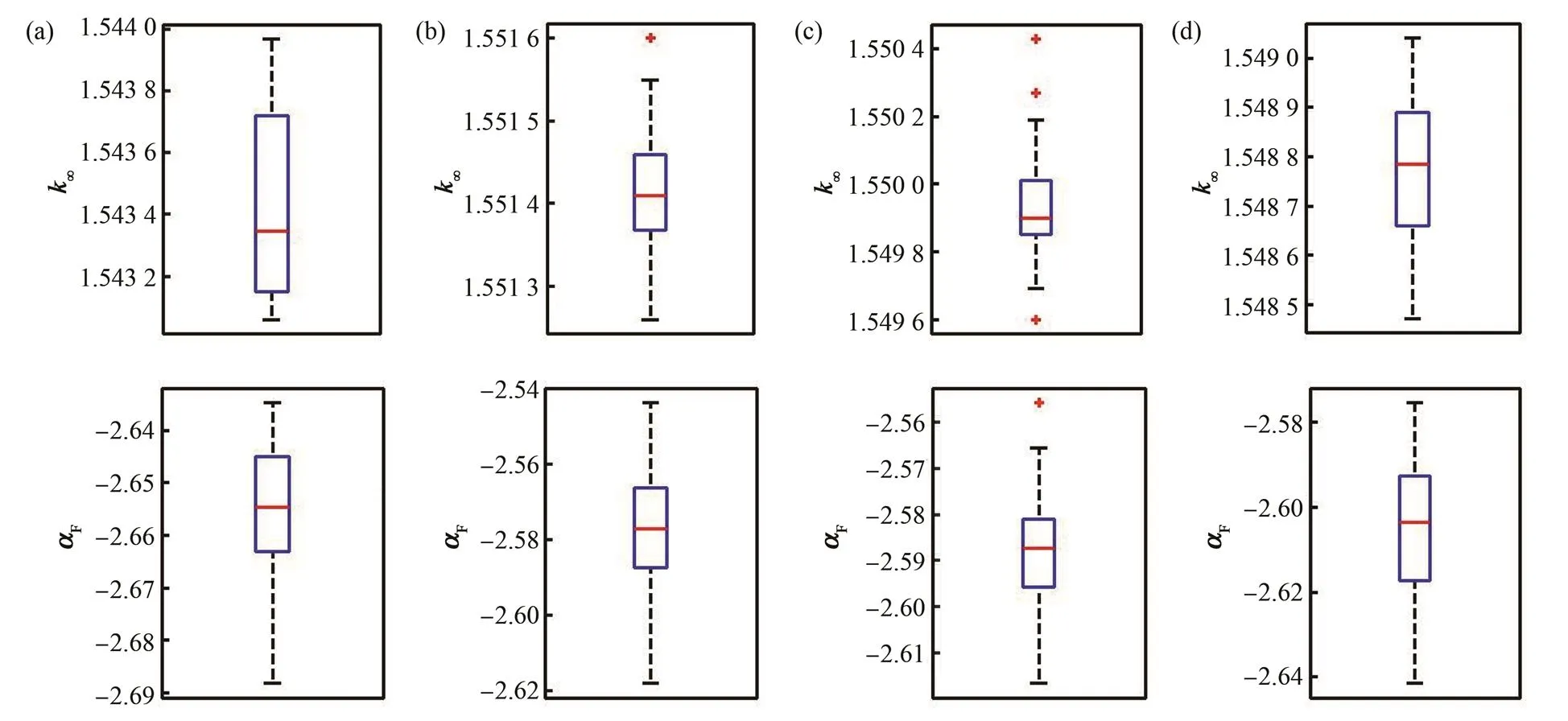
图3 不同随机填充计算结果统计 (a) 体积等效规则填充，(b) 扰动的规则填充，(c) 随机的规则填充，(d) 完全随机填充

2.2.2 集中球心

在集中于球心规则填充的基础上，通过改变立方体栅元的长度，改变包覆颗粒之间的平均距离，计算结果见表3。随着填充栅元的逐步变大，包覆颗粒之间的平均距离逐渐从1.3461 cm增加至2.5040cm，所有包覆颗粒到燃料球心的平均距离也相应地从0.981 4 cm增加至1.825 7 cm，无限增殖因数∞逐渐从1.664 14减小至1.547 34，相差0.1168，燃料温度系数逐渐从−1.434×10−5K−1增加至−2.604×10−5K−1，增加了80%。

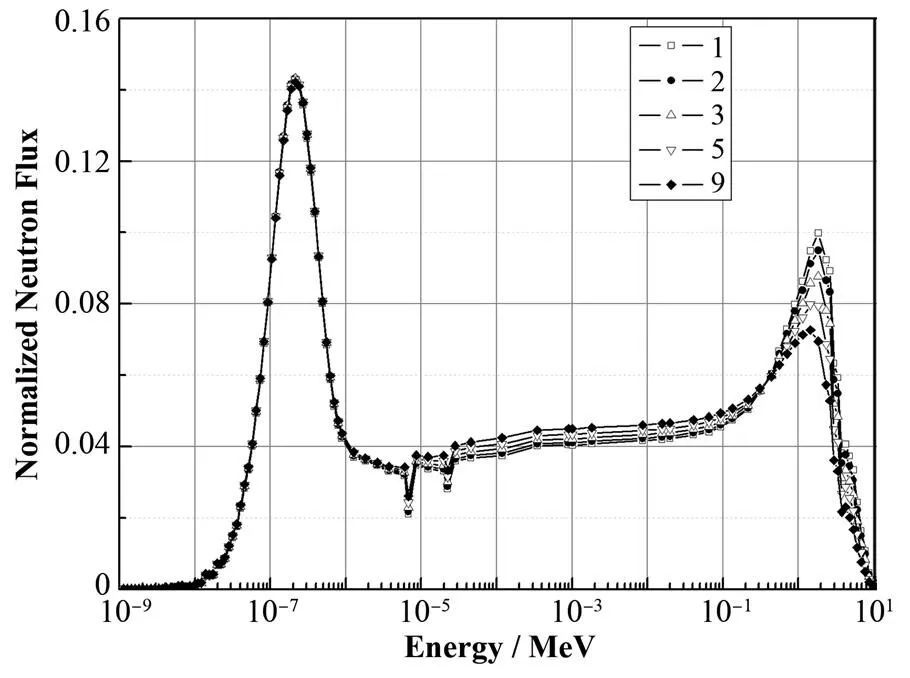
图4 燃料区域归一化中子能谱分布

为分析这一变化原因，提取出燃料中的能谱，见图4。图4中的曲线编号与表3中序号一致，包覆颗粒的集中导致燃料区内慢化减弱，能谱变硬。根据定义分别计算了4因子：、、和，见图5。图5中的横坐标对应于表3中的序号。

图5 4因子变化曲线

4因子中，逃脱俘获共振因数的变化最为剧烈。降低约9.2%，增加约9.3‰，增加约3.7‰，增加约1.7‰。随着包覆颗粒的密集，丹可夫效应增强，燃料核吸收共振中子的能力显著降低，导致无限增殖因数增加，燃料温度负反馈减弱。

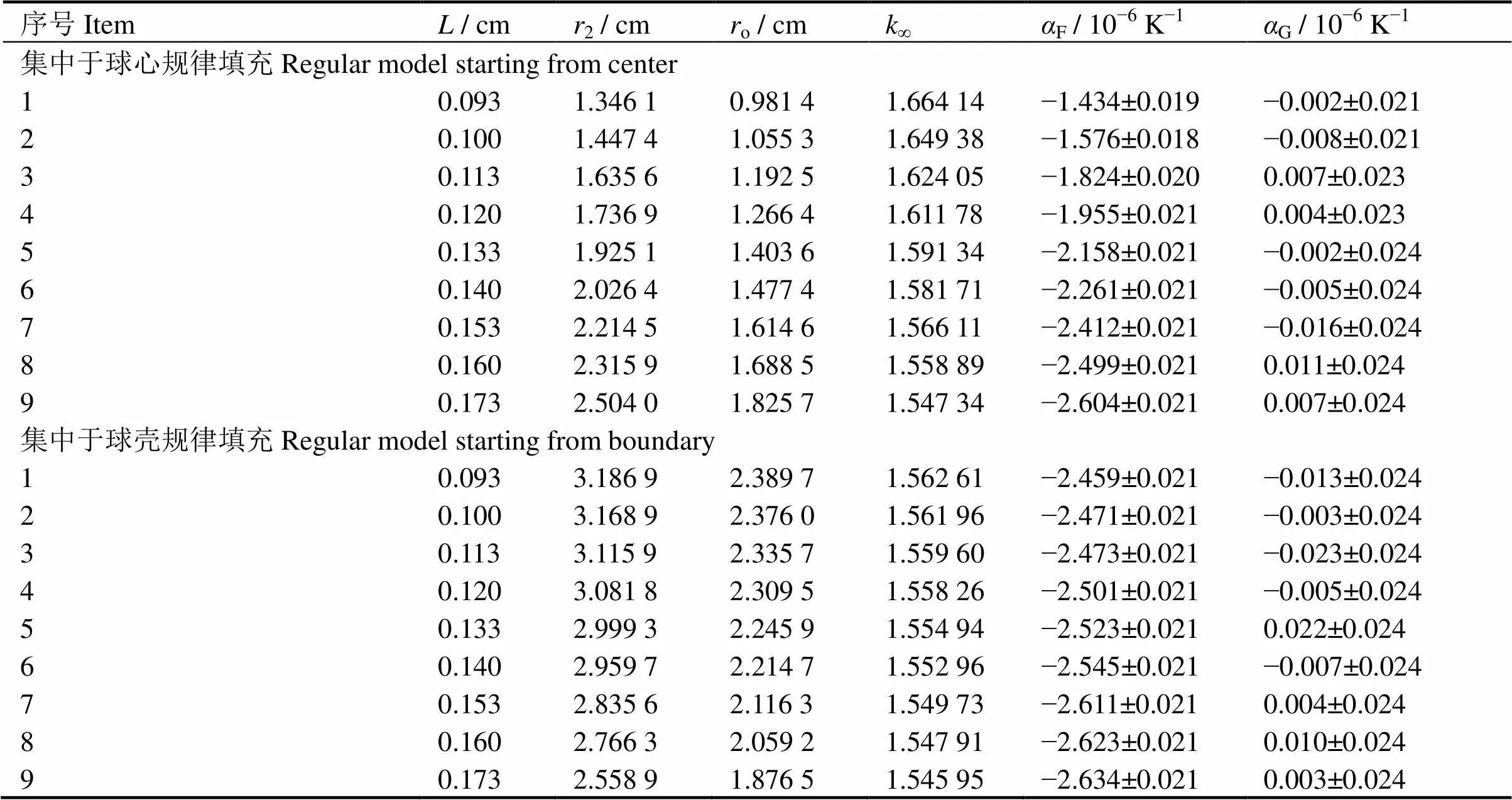
表3 规律填充的计算结果

3 结语

本文通过MATLAB程序实现了球形燃料元件中包覆颗粒燃料的特定分布形式，并以TMSR-SF1设计中选用的包覆颗粒燃料为分析基准，结合MCNP程序计算分析了燃料中包覆颗粒分布对中子物理特性的影响，通过计算结果分析形成以下结论：

1) 燃料中包覆颗粒的分布对无限增殖因数和燃料温度系数有较大影响，对石墨慢化剂温度系数的影响则较小。两种指定规律填充的计算结果均表明，包覆颗粒的集中会导致逃脱共振吸收能力增强与燃料填充区内石墨基体慢化能力的下降，无限增殖因数会随之增大，燃料的温度反应性系数会随着减小。

2) 完全随机填充模式和实际情况更接近，建模和计算所需的时间更长。相对随机填充而言，随机的规则填充的包覆颗粒相对较为集中，因此无限增殖因数会被高估约1.16×10−3，燃料的温度反应性系数会被低估 1.5%。

3) 体积等效规则填充方式是在全堆芯蒙特卡罗计算中使用的方式，建模和计算所需的时间最短，但会造成不同位置燃料球内包覆颗粒的切割，包覆颗粒的分布也更为分散，因此无限增殖因数被低估约5×10−3，燃料的温度反应性系数被高估2%。

1 Allen T, Ball S, BlandfordE,. Preliminary fluoride salt-cooled high temperature reactor (FHR) subsystems definition, functional requirement definition and licensing basis event (LBE) identification white paper[R]. Berkeley, USA: University of California, UCBTH-12-001, 2012.

2 Forsberg C, Hu LW, Richard J,. Fluoride-salt-cooled high temperature test reactor (FHTR): goals, options, ownership, requirements, design, licensing, and support facilities[R]. USA: Massachusetts Institute of Technology, MIT-ANP-TR-154, 2014.

3 Sun K, Hu L, Forsberg C. Neutronic design features of a transportable fluoride-salt-cooled high-temperature reactor[J]. ASME Journal of Nuclear Engineering and Radiation Science, 2016, 2(3): 031003. DOI: 10.1115/1.4032873.

4 Hong-Chul Kim, Song Hyun Kim, Jong Kyung Kim. A new strategy to simulate a random geometry in a pebble-bed core with the Monte Carlo code MCNP[J]. Annals of Nuclear Energy, 2011, 38(9): 1877−1883. DOI: 10.1016/j.anucene.2011.05.012.

5 Amin A, Naser V, Mohammad B G. An exact MCNP modeling of pebble bed reactors[J]. World Academy of Science, Engineering and Technology, 2011,5(11): 190−1913. DOI: 10.13140/2.1.3136.8321.

6 Wei J. Neutronic analysis of stochastic distribution of fuel particles in very high temperature gas-cooled reactors[D]. USA: University of Michigan,2008.

7 常鸿, 杨永伟, 经荥清. 球床式高温气冷堆初次临界物理计算的蒙特卡罗方法模型分析[J]. 核动力工程, 2005, 26(5):419−424. DOI: 10.3969/j.issn.0258-0926.2005.05. 001.

CHANG Hong, YANG Yongwei, JING Xingqing. Model analysis of Monte-Carlo method for first criticality physics calculation in pebble bed high temperature gas-cooled reactor[J]. Nuclear Power Engineering, 2005, 26(5):419−424. DOI: 10.3969/j.issn.0258-0926.2005.05. 001.

8 Pelowitz D B. MCNP6TMuser’s manual[R]. Los Alamos, NM, USA: Los Alamos National Laboratory, LA-CP-13-00634, 2013.

9 Forrest B B, William R M. Stochastic geometry capability in MCNP5 for the analysis of particle fuel[J]. Annals of Nuclear Energy, 2004, 31(17): 2039−2047. DOI: 10.1016/j.anucene.2004.08.006.

10 Zuo JX, Jing JP, Bi JS,. Framework analysis of fluoride salt-cooled high temperature reactor probabilistic safety assessment[J]. Nuclear Science and Techniques, 2015, 26(5): 050602. DOI: 10.13538/j.1001-8042/nst.26.050602.

11 Zhang ZH, Xia XB, Cai J,. Simulation of radiation dose distribution and thermal analysis for the bulk shielding of an optimized molten salt reactor[J]. Nuclear Science and Techniques, 2015, 26(4): 040603. DOI: 10.13538/j.1001-8042/nst.26.040603.

12 Ji RM, Li MH, Zou Y,.Impact of photoneutrons on reactivity measurements for TMSR-SF1[J]. Nuclear Science and Techniques, 2017, 28(6): 76.DOI: 10.1007/s41365-017-0234-7.

13 刘马林, 刘荣正, 李自强, 等. 颗粒学在高温气冷堆核能工程中的应用[J]. 中国粉体技术, 2014,20(4): 1−7. DOI: 10.13732/j.issn.1008-5548.2014.04.001.

LIU Malin, LIU Rongzheng, LI Ziqiang,.Application of particuology in high temperature gas cooled nuclear reactor engineering[J].China Powder Science and Technology, 2014,20(4): 1−7. DOI: 10. 13732/j.issn.1008-5548.2014.04.001.

Effect of TRISO-particles distributions in pebble fuel

JI Ruimin1,2YAN Rui1LI Xiaoxiao1DAI Ye1LIU Guimin1ZOU Yang1

1(Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Jiading Campus,Shanghai 201800,China) 2(University of Chinese Academy of Sciences,Beijing 100049,China)

Packing fraction of tristructural-isotropic (TRISO) particles in pebble fuel is lower than 10% in general, which leads to great randomness in distribution, resulting in various challenges in neutronics modeling, such as double heterogeneity effect, preserving exact number of particles, and their random distributions in pebble.This study aims to verify the calculations, the infinite pebble fuel with refectory boundary conditions based on the thorium-based molten salt reactor with solid fuel (TMSR-SF1) pebble design using Monte-Carlo code MCNP6 ver1.0 and ENDF/B VII.0.Four types of models of TRISO particles have been performed based on MATLAB, the equivalently filled regular model, the disturbed regular model, the randomly filled regular model, and the fully random model.The neutronic effect of various modeling approaches was quantitatively evaluated.The results show that the four kinds of modeling methods form different randomness. The clustering of the coated particles enhances the Dancof effect which raises the neutron absorption probability in the fuel. As a result, the infinite multiplication factor is increased while the fuel temperature coefficient is decreased.

Coated particle fuel, Infinite multiplication factor, Temperature coefficient

JI Ruimin, female, born in 1984, graduated from Shanghai Institute of Applied Physics, Chinese Academy of Sciences with a master’s degree in 2008, focusing on the study of reactor physics

LIU Guimin, E-mail: liuguimin@sinap.ac.cn; YAN Rui,E-mail: yanrui@sinap.ac.cn

2017-03-24, accepted date: 2017-04-20

TL99

10.11889/j.0253-3219.2017.hjs.40.100604

冀锐敏，女，1984年出生，2008年于中国科学院上海应用物理研究所获硕士学位，主要从事反应堆物理研究

刘桂民，E-mail: liuguimin@sinap.ac.cn；严睿，E-mail: yanrui@sinap.ac.cn

2017-03-24，

2017-04-20

Supported by Strategic PriorityResearch Programof Chinese Academy of Sciences (No.XDA02010000)

中国科学院战略性先导科技专项(No.XDA02010000)资助