关于一个参量化的全平面Hilbert积分不等式

曾志红, 杨必成

(1. 广东第二师范学院学报编辑部, 广州 510303； 2. 广东第二师范学院数学系, 广州 510303)

关于一个参量化的全平面Hilbert积分不等式

曾志红1, 杨必成2*

(1. 广东第二师范学院学报编辑部, 广州 510303； 2. 广东第二师范学院数学系, 广州 510303)

探讨了一个新的参量化的全平面Hilbert积分不等式：建立2个权函数，运用带权的Hölder不等式，应用实分析技巧，引入非零的独立参量a、b、、β以及满足关系σ+μ=<1-β的参数σ、μ,得到一个新的全平面非齐次核的具有最佳常数因子K(σ)且含中间变量的Hilbert型积分不等式及其等价式和特殊参数下的齐次与非齐次核不等式.

权函数； 全平面Hilbert积分不等式； 等价式； 最佳常数

Keywords： weight function; Hilbert’s integral inequality in the whole plane; equivalent form; best possible constant factor

(1)

这里,常数因子π为最佳值.

基于式(1)的Hilbert积分不等式的部分推广形式[2-7]有-1齐次核k(x,y)的；有引入一对共轭指数，或引入贝塔函数及独立参量(0,)，或引入2对共轭指数(p,q)、(r,s) (p,r>1,1/p+1/q=1/r+1/s=1)及独立参数>0得到的. 这些Hilbert积分不等式的研究区域均为第一象限. 目前，在全平面上研究Hilbert积分不等式的文献还比较少.

2007年,YANG[8]得到全平面非齐次核的具有最佳常数因子的Hilbert型积分不等式:

(2)

随后,文献[9-16]继续讨论了这一课题.

本文在文献[8]的基础上引入独立参量及含指数函数的中间变量，运用权函数方法和实分析技巧，建立如下一个类似式(2)的全平面齐次核的具有最佳常数因子的Hilbert型积分不等式:

(3)

其中，σ,μ>0,σ+μ=. 并进一步探讨了其更一般的形式、等价式及特殊参数下的齐次与非齐次核不等式.

1 权函数与初始不等式

定义1设a,b≠0,σ,μ>0,σ+μ=<1-β. 定义如下权函数:

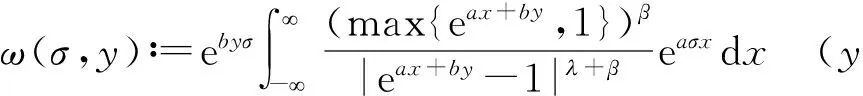
(4)

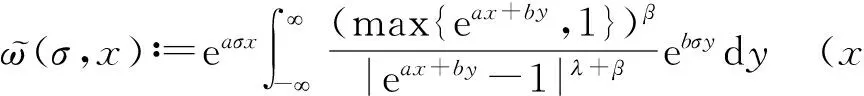
(5)

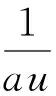
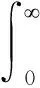
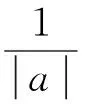
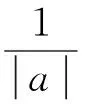
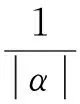
(6)

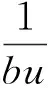
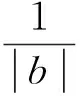
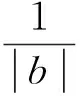
(7)

定理1设p>1,1/p+1/q=1,a,b≠0,σ,μ>0,σ+μ=<1-β,则

K(σ)∶=Kb1/pKa1/q=

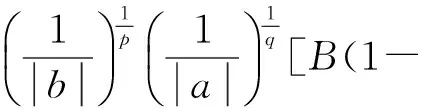
(8)

f(x)≥0,x,且. 则有如下不等式:

(9)

证明由带权的Hölder不等式[17]及式(7),有

(10)

下证式(10)中间取严格不等号. 否则,对于某个y,使式(10)中间取等号,有不全为0的常数A、B，使a.e.于[17]. 若A=0,则B=0,这与A、B不全为0的条件矛盾. 不妨设A≠0,则a.e.于. 这与条件矛盾. 由式(10)、(6)及交换积分次序的Fubini定理[18],有

(11)

再由式(7)、(8),可得式(9). 证毕.

2 具有最佳常数因子的等价式

定理2设p>1,1/p+1/q=1,a,b≠0,σ,μ>0,σ+μ=<1-β,K(σ)如式(8)所示. 若及,则有如下与式(9)等价的不等式:

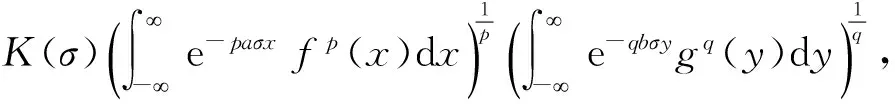
(12)

这里,式(12)与式(9)的常数因子K(σ)均为最佳值. 特别当a=b=1时,有非齐次核的具有最佳常数因子k(σ)∶=[B(1--β,σ)+B(1--β,μ)]的等价不等式:

(13)

(14)

证明由Hölder不等式,有

(15)

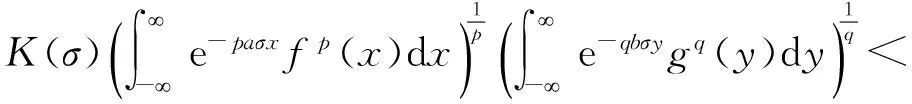
由此可得式(9),而且式(9)与式(12)等价.

任意给足够大的n+,定义集合Ea∶={x;ax≥0},Fb∶={y;by≤0},及函数

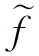
则

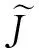
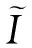
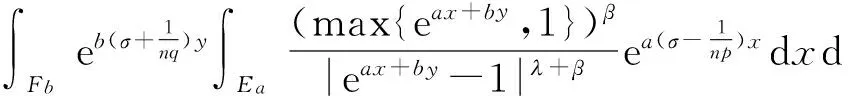
作变换u=eax+by,有

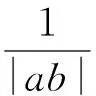
(16)

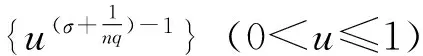
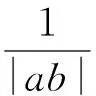
(17)

及K(σ)≤k. 故k=K(σ)是式(12)的最佳值. 式(9)的常数因子K(σ)必是最佳值,否则,由式(15),必导出式(12)的常数因子也不是最佳值的矛盾. 证毕.

评注在式(12)与式(9)中,令a=1,b=-1,以eg(y)取代g(y),则有及如下具有最佳常数因子的齐次核等价不等式:

(18)

(19)

当β=-时,式(18)变为式(3).

[1] SCHUR I. Bernerkungen zur theorie der beschränkten Billnearformen mit unendlich vielen veranderlichen [J]. Journal Für Die Reine und Angewandte Mathematik,1911,140:1-28.

[2] HARDY G H. Note on a theorem of Hilbert concerning series of positive terms [J]. Proceedings of the London Mathematical Society,1925,23(2):45-46.

[3] HARDY G H,LITTLEWOOD J E,POLYA G. Inequalities [M]. Cambridge:Cambridge University Press,1952.

[4] MITRINOVIC D S,PECARIC J E,FINK A M. Inequalities involving functions and their integrals and derivatives [M]. Boston:Kluwer Academic Publishers,1991.

[5] YANG B C. On Hilbert’s integral inequality [J]. Journal of Mathematical Analysis and Applications,1998,220:778-785.

[6] YANG B C. A note on Hilbert’s integral inequality [J]. Chinese Quarterly,1998,13(4):83-86.

[7] YANG B C. On an extension of Hilbert’s integral inequali-ty with some parameters [J]. Australian Journal of Mathe-matical Analysis and Applications,2004,1(1):1-8.

[8] YANG B C. A new Hilbert’s type integral inequality [J]. Soochow Journal of Mathematics,2007,33(4)：849-859.

[9] 杨必成. 一个新的参量化Hilbert型积分不等式[J]. 吉林大学学报(理学版),2008,46(6):1085-1090.

YANG B C. A new Hilbert-type integral inequality with some parameters[J]. Journal of Jilin University(Science Edition),2008,46(6):1085-1090.

[10] XIN D M,YANG B C. A Hilbert-type integral inequality in the whole plane with the homogeneous kernel of degree -2[J]. Journal of Inequalities and Applications,2011(1):1-11.

[11] WANG A Z,YANG B C. A new Hilbert-type integral inequality in the whole plane with the non-homogeneous kernel[J]. Journal of Inequalities and Applications,2011(1):123-131.

[12] XIE Z T,RAJA RAMA GANDHI K,ZENG Z. A new Hilbert-type integral inequality with the homogeneous kernel of real degree form and the integral in whole plane [J]. Bulletin of Society for Mathematical Services & Applications,2013,2(1):95-109.

[13] XIE Z T,ZENG Z. A new Hilbert-type inequality in whole plane with the homogeneous kernel of degree 0 [J]. I-manager’s Journal on Mathematics,2013,2(1):13-19.

[14] XIE Z T,ZENG Z,SUN Y F. A new Hilbert-type inequality with the homogeneous kernel of degree-2 [J]. Advances and Applications in Mathematical Sciences,2013,12(7):391-401.

[15] YANG B C,CHEN Q. Two kinds of Hilbert-type integral inequalities in the whole plane [J]. Journal of Inequalities and Applications,2015(1):1-11.

[16] RASSIAS M T,YANG B C. A Hilbert-type integral inequality in the whole plane related to the hypergeometric function and the beta function [J]. Journal of Mathematical Analysis and Applications,2015,428(2):1286-1308.

[17] 匡继昌. 常用不等式[M]. 济南:山东科技出版社,2004.

[18] 匡继昌. 实分析与泛函分析(续论) [M]. 北京:高等教育出版社,2015.

A Parametric Hilbert’s Integral Inequality in the Whole Plane

ZENG Zhihong1, YANG Bicheng2*

(1. Editorial Department of Journal, Guangdong University of Education, Guangzhou 510303, China;2. Department of Mathematics, Guangdong University of Education, Guangzhou 510303, China)

A new parametric Hilbert’s integral inequality in the whole plane is discussed. Two weight functions are established. By using the weighted Hölder’s inequality, the real analysis techniques, and by introducing the non-zero independent parametersa,b,,βand the parametersσ,μsatisfyingσ+μ=<1-β, a new Hilbert-type integral inequality with intermediate variable, the best constant factorK(σ) and non-homogeneous kernel is obtained, as well as its equivalent inequality and the inequalities with homogeneous or non-homogeneous kernel under special parameters.

2017-03-31 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(61370186);广东第二师范学院教授、博士科研专项基金项目 (2015ARF25)

*通讯作者:杨必成，教授，Email:bcyang@gdei.edu.cn.

O178

A

1000-5463(2017)05-0100-04

【中文责编：庄晓琼 英文审校：肖菁】