用条件(PWPE)刻画的序幺半群

王 田, 梁星亮

(1. 甘肃中医药大学(定西校区)理科部, 定西 743000； 2. 兰州大学数学与统计学院, 兰州 730000； 3. 陕西科技大学文理学院, 西安 710021)

用条件(PWPE)刻画的序幺半群

王 田1, 梁星亮2,3*

(1. 甘肃中医药大学(定西校区)理科部, 定西 743000； 2. 兰州大学数学与统计学院, 兰州 730000； 3. 陕西科技大学文理学院, 西安 710021)

借助S-系理论及序半群理论的方法,在序S-系范畴中引入了条件(PWPE),刻画了循环(Rees商)序S-系满足这一条件的序幺半群的结构特征. 进一步地,给出了Rees商序S-系的条件(PWPE)与其他平坦性质一致的序幺半群的刻画,并推广了条件(PWP)的相关结果．

条件(PWPE)； 序S-系； 序幺半群

Keywords： condition(PWPE);S-poset; pomonoid

序S-系理论作为序幺半群的一种表示与同调代数具有密切的联系,序S-系平坦性质的研究是该理论中重要的研究内容之一,已取得了丰富的研究成果[1-12]. 20世纪80年代,FAKHRUDDIN[1-2]最早研究了序S-系的平坦性质. 2005年,SHI等[8-9]将S-系范畴中的条件(P)和平坦性推广至序S-系范畴中,并证明了每一个满足条件(P)的序S-系是序平坦的. 进一步地,引入了序平坦序S-系的主弱形式,称之为序主弱平坦序S-系,并利用该性质刻画了左PP、左PSF序幺半群. 2009年,GOLCHIN和REZAEI[4]在序S-系范畴中利用子拉回图定义了条件(PWP),该条件是条件(P)的主弱形式. 由文献[4]可以得到条件(PWP)与序主弱平坦性之间的关系:

条件(PWP)⟹序主弱平坦性.

为进一步探索平坦性质在序S-系中的应用,本文通过引入条件(PWP)的一种推广形式,称之为条件(PWPE),建立了该条件与序主弱平坦性之间的联系,研究了循环(Rees商)序S-系满足这一条件的序幺半群的结构特征,进而推广了条件(PWP)的已有相关结果.

1 预备知识

设S是序幺半群,1是其单位元,E(S)表示S中所有幂等元的集合,文中未说明的术语和事实见文献[3,5,7]. 设A是一个带有偏序≤的集合,f是A×S到A的映射,简记为f(a,s)=as. 如果对任意的a,a′A,s,s′S,满足以下条件:

(1)a(ss′)=(as)s′, 以及a·1=a.

(2)a≤a′推出as≤a′s,并且s≤s′推出as≤as′.

则称(A,f)是一个序右S-系,或称S序右作用于A上[1]. 为了方便起见,简记为AS或A. 类似地可以定义序左S-系SA.

设ρK是由K决定的Rees商序同余. 称序幺半群S的凸的真右理想K是强左零化的[4-5],如果对任意的tS,x,ySK,由[x]ρKt≤[y]ρKt推出xt≤yt.

称序右S-系A满足条件(PWP)[4],如果对任意的a,a′A,sS,若as≤a′s,则存在a″A,u,vS,使得a=a″u,a′=a″v,且us≤vs.

称序右S-系A是序主弱平坦的[9],如果对任意的a,a′A,sS,若a⊗s≤a′⊗s在A⊗S中成立,则a⊗s≤a′⊗s在A⊗Ss中成立.

首先给出满足条件(PWPE)的序S-系的定义.

定义1称序右S-系A满足条件(PWPE),如果对任意的a,a′A,sS,as≤a′s,存在a″A,u,vS,e,fE(S),使得ae=a″ue,a′f=a″vf,es=s=fs且us≤vs.

注记1显然,在定义1中,当e=f=1时,条件(PWPE)就是条件(PWP). 因此,每一个满足条件(PWP)的序S-系都满足条件(PWPE). 但由文献[5]的例3.11可知其逆不成立. 另外,由定义1可知SS和ΘS都满足条件(PWPE).

下面建立条件(PWPE)与序主弱平坦性之间的关系:

命题1设A是序右S-系. 若A满足条件(PWPE),则A是序主弱平坦的.

证明假设A是满足条件(PWPE)的序右S-系. 若a⊗s≤a′⊗s在A⊗S中成立,则由文献[9]的推论3.3知as≤a′s. 根据假设,存在a″A,u,vS和e,fE(S),使得ae=a″ue,a′f=a″vf,es=s=fs且us≤vs. 因此,在A⊗Ss中有

a⊗s=a⊗es=ae⊗s=a″ue⊗s=a″⊗ues=a″⊗us≤

a″⊗vs=a″⊗vfs=a″vf⊗s=a′f⊗s=a′⊗fs=a′⊗s,

故A是序主弱平坦的. 证毕.

利用命题1可给出序群的一个新的等价刻画:

推论1对任意序幺半群S,以下条件等价:

(1)所有的序S-系满足条件(PWPE),且|E(S)|=1;

(2)S是序群.

证明(1)⟹(2). 假设所有的序S-系满足条件(PWPE). 根据命题1,所有的序S-系是序主弱平坦的，则由文献[6]的定理2.3知S是正则序幺半群. 又因为|E(S)|=1,容易得到S就是序群.

(2)⟹(1)显然成立. 证毕.

2 主要结果

本节主要研究满足条件(PWPE)的序S-系的同调分类问题. 首先,由定义1可给出循环序S-系满足条件(PWPE)的序幺半群的刻画：

命题2设ρ是S上的序右同余,则循环序S-系S/ρ满足条件(PWPE)当且仅当对∀x,y,tS，

[x]ρt≤[y]ρt⟹(∃u,vS)(e,fE(S))((xe)ρ(ue)∧

(yf)ρ(vf)∧et=t=ft∧ut≤vt).

推论2[4]设ρ是S上的序右同余,则循环序S-系S/ρ满足条件(PWP)当且仅当对任意的x,y,tS,若[x]ρt≤[y]ρt,则存在u,vS,使得xρu,yρv且ut≤vt.

由命题2可得以下推论:

推论3设sS,则主右理想sS满足条件(PWPE)当且仅当对∀x,y,tS，

sxt≤syt⟹(∃u,vS)(e,fE(S))(sxe=sue∧syf=

svf∧et=t=ft∧ut≤vt).

为了刻画满足条件(PWPE)的Rees商序S-系,给出以下定义:

定义2称序幺半群S的凸的真右理想K是强E-左零化的,如果对∀tS,x,ySK,

[x]ρKt≤[y]ρKt⟹(∃u,vS)(e,fE(S))(et=t=

ft∧ut≤vt∧xe≠ue⟹xe,ueK∧yf≠vf⟹yf,vfK).

注记2显然,S的每一个凸的强左零化真右理想都是强E-左零化的. 然而,文献[5]的例3.11说明了反之不然.

下面给出Rees商序S-系满足条件(PWPE)的序幺半群的刻画.

定理1设K是序幺半群S的凸的真右理想，则 Rees 商序右S-系S/K满足条件(PWPE)当且仅当K是强左稳定的和强E-左零化的.

证明必要性. 假设S/K满足条件(PWPE). 则由命题1知,S/K是序主弱平坦的,于是由文献[5]的引理3.7知,K是强左稳定的. 下证K是强E-左零化的. 设[xt]≤[yt],其中tS,x,ySK. 因为S/K满足条件(PWPE),由命题2知,存在u,vS,e,fE(S),使得(xe)ρK(ue),(yf)ρK(vf),et=t=ft且ut≤vt. 根据ρK的定义,由xe≠ue和yf≠vf得xe,ueK和yf,vfK. 因此,K是强E-左零化的.

充分性. 假设K是凸的强左稳定和强E-左零化真右理想. 为了证明S/K满足条件(PWPE),只需验证S满足命题2的条件即可. 若x,y,tS满足[xt]≤[yt],则由文献[3]的引理3知xt≤yt,或者存在k,k′K使得xt≤k且k′≤yt. 如果xt≤yt,则只需取u=x,y=v,e=f=1即可;否则,将考虑以下4种情形:

情形1.x,yK. 取u=v=x,e=1=f即可;

情形2.xK,yK. 因为K是强左稳定的,并且ytS,所以存在kK使得kyt≤yt,于是取u=ky,v=y且e=1=f即可;

情形3.xK,yK. 类似于情况2;

情形4.x,yK. 因为K是强E-左零化的,所以存在u,vS,e,fE(S),使得xe≠ue⟹xe,ueK,yf≠vf⟹yf,vfK,et=t=ft且ut≤vt,故(xe)ρK(ue),(yf)ρK(vf).

综上所述,S/K满足条件(PWPE). 证毕.

推论4[4]设K是序幺半群S的凸的真右理想，则Rees商序右S-系S/K满足条件(PWP)当且仅当K是强左稳定的和强左零化的.

正如命题1所述,条件(PWPE)⟹序主弱平坦,但以下例子说明了反之不然.

例1[4]设S={0,1,r,s,t}是满足如下运算

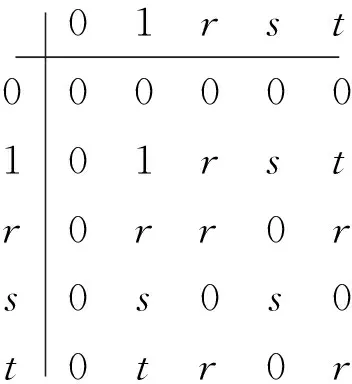
的幺半群,并且S仅有的非平凡序关系为t<0且r<0. 令K={0,r}，则(S,≤)是一个序幺半群,并且容易验证K是凸的强左稳定真右理想. 由文献[4]的例6.3知,S/K是序主弱平坦的. 然而,根据定理1,S/K不满足条件(PWPE). 这是因为1,tSK,且[1]t≤[t]t,但不存在元素u,vS和e,fE(S)满足1e≠ue⟹1e,ueK,tf≠vf⟹tf,vfK,et=t=ft且ut≤vt,从而K不是强E-左零化的.

接下来考虑Rees商序S-系的条件(PWPE)与其他平坦性质一致的序幺半群的刻画.

定理2对任意序幺半群S,以下条件等价:

(1)所有满足条件(PWPE)的Rees商序S-系S/K满足条件(PWP);

(2)S的每一个凸的强左稳定和强E-左零化真右理想是强左零化的.

证明(1)⟹(2). 假设K是S的凸的强左稳定和强E-左零化真右理想. 则由定理1知,S/K满足条件(PWPE). 根据条件(1),S/K满足条件(PWP),于是由文献[5]的引理3.8知,K是强左零化的.

(2)⟹(1). 设K是S的凸的右理想,并且S/K满足条件(PWPE). 如果K是S的真右理想,那么由定理1知,K是强左稳定的和强E-左零化的. 从而根据条件(2),K是强左零化的理想,进而由文献[5]的引理3.8知,S/K满足条件(PWP). 如果K=S,显然,S/K≅ΘS满足条件(PWP),即结论成立.

定理3对任意序幺半群S,以下条件等价:

(1)所有满足条件(PWPE)的Rees商序S-系S/K满足条件(P);

(2)S是弱右reversible序幺半群,且S中没有真的强左稳定和强E-左零化凸右理想K使得|K|>1.

证明(1)⟹(2). 由于ΘS满足条件(PWPE),所以根据条件(1),ΘS满足条件(P). 由文献[3]的定理1,S是弱右reversible序幺半群. 反设S有真的强左稳定和强E-左零化凸右理想K且|K|>1,则由定理1知,S/K满足条件(PWPE). 从而根据条件(1),S/K满足条件(P),于是由文献[7]的引理1.8知,|K|=1,矛盾.

(2)⟹(1). 令K是S的凸的右理想,并且S/K满足条件(PWPE). 如果K是S的真右理想, 那么由定理1知,K是强左稳定的和强E-左零化的. 根据条件(2),|K|=1,故S/K满足条件(P). 如果K=S,因为S是弱右reversible序幺半群,所以根据文献[3]的定理1,S/K≅ΘS满足条件(P),故结论成立. 证毕.

类似地,可以证明下面2个定理.

定理4对任意序幺半群S,以下条件等价:

(1)所有满足条件(PWPE)的Rees商序S-系S/K是强平坦的;

(2)S是左collapsible序幺半群,且S中没有真的强左稳定和强E-左零化凸右理想K使得|K|>1.

定理5对任意序幺半群S,以下条件等价:

(1)所有满足条件(PWPE)的Rees商序S-系S/K是投射的;

(2)S有左零元,且S中没有真的强左稳定和强E-左零化凸右理想K使得|K|>1.

最后给出Rees商序S-系的条件(PWPE)与自由性一致的序幺半群的结构特征.

定理6对任意序幺半群S,以下条件等价:

(1)所有满足条件(PWPE)的Rees商序S-系S/K是自由的;

(2)|S|=1.

证明(1)⟹(2). 因为ΘS满足条件(PWPE),所以由假设知ΘS是自由的. 根据文献[3]的定理1,|S|=1.

(2)⟹(1)显然. 证毕.

在定理1～定理6中,若将序S-系和序幺半群中的偏序均取作平凡序时,就可以直接得到S-系理论的相应经典结果[13].

[1] FAKHRUDDIN S M. Absolute flatness and amalgams in pomonoids [J]. Semigroup Forum,1986,33:15-22.

[2] FAKHRUDDIN S M. On the category ofS-posets [J]. Acta Scientiarum Mathematicarum(Szeged),1998,52(1/2):85-92.

[3] BULMAN-FLEMING S,GUTERMUTH D,GILMOUR A,et al. Flatness properties ofS-posets [J]. Communications in Algebra,2006,34(4):1291-1317.

[4] GOLCHIN A,REZAEI P. Subpullbacks and flatness pro-perties ofS-posets [J]. Communications in Algebra,2009,37(6):1995-2007.

[5] LIANG X L,LUO Y F. On condition (PWP)wforS-posets [J]. Turkish Journal of Mathematics,2015,39:795-809.

[6] QIAO H S,LI F. When allS-posets are principally weakly flat [J]. Semigroup Forum,2007,75:536-542.

[7] QIAO H S,LIU Z K. On the homological classification of pomonoids by their Rees factorS-posets [J]. Semigroup Forum,2009,79(2):385-399.

[8] SHI X P,LIU Z K,WANG F G,et al. Indecomposable,projective,and flatS-posets [J]. Communications in Algebra,2005,33:235-251.

[9] SHI X P. Strongly flat and po-flatS-posets [J]. Communications in Algebra,2005,33(12):4515-4531.

[10] ZHANG X,LAAN V. On homological classification of pom-onoids by regular weak injectivity properties ofS-posets [J]. Central European Journal of Mathematics,2007,5(1):181-200.

[11] ZHANG X,LAAN V. On injective hulls ofS-posets [J]. Semigroup Forum,2015,91:62-70.

[12] 张霞,徐彦涛. 偏序群S上S-偏序系的内射包 [J]. 华南师范大学学报(自然科学版),2014,46(4):12-15.

ZHANG X,XU Y T. Injective hulls ofS-posets over a pogroupS[J]. Journal of South China Normal University(Natural Science Edition),2014,46(4):12-15.

[13] GOLCHIN A,MOHAMMADZADEH H. On condition (PWPE) [J]. Southeast Asian Bulletin of Mathematics,2009,33:245-256.

Characterization of Pomonoids by Condition (PWPE)

WANG Tian1, LIANG Xingliang2,3*

(1. Science Department, Gansu University of Chinese Medicine (Dingxi Campus), Dingxi 743000, China；2. School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000, China；3. College of Arts and Science, Shaanxi University of Science and Technology, Xi’an 710021, China)

By usingS-act theory and ordered semigroup theory, condition(PWPE) in the category ofS-posets is introduced, and pomonoids over which cyclic (Rees factor)S-posets satisfy this new condition are characterized. Moreover, a classification of pomonoids is given for which Rees factorS-posets satisfying condition(PWPE) have some other flatness properties and vice versa. As applications, some important results on condition(PWPE) are extended.

2016-05-16 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(11501451);陕西省自然科学基础研究计划项目(2017JQ1026)

*通讯作者:梁星亮,讲师,Email:lxl_119@126.com.

O152.7

A

1000-5463(2017)05-0104-04

【中文责编：庄晓琼 英文审校：肖菁】