圆锥曲线切点弦的一个统一性质——对一道高考解几试题的探究所得

陈学忠

福建省仙游第一中学 (351200)

圆锥曲线切点弦的一个统一性质
——对一道高考解几试题的探究所得

陈学忠

福建省仙游第一中学 (351200)

2016高考全国卷Ⅰ文科试题题20是：

如图1，在直角坐标系xOy中，直线l：y=t(t≠0)交y轴于点M，交抛物线C：y2=2px(p>0)于点P，M关于点P的对称点为N，连结ON并延长交C于点H.

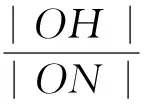
(2)除H以外，直线MH与C是否有其它公共点？说明理由.

这是一道难度适中内涵丰富，值得深入探究的高考试题，本文拟对此进行一番探究.

结论1.1 已知抛物线C：y2=2px(p>0)，过y轴上的点M且平行于x轴的直线与抛物线C、弦OH(O为坐标原点)分别交于点P、N，若MP=PN，则ON=NH，且直线MH与抛物线C相切于点H.

一、逆向探究：探究结论的逆命题

探究1 结论1.1的逆命题成立吗？即若直线MH与抛物线C相切于点H，那么MP=PN且ON=NH能否成立？

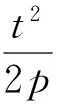
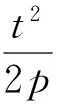
结论1.2 已知抛物线C：y2=2px(p>0)，过y轴上的点M且平行于x轴的直线与抛物线C、弦OH(O为坐标原点)分别交于点P、N，若直线MH与抛物线C相切于点H，则MP=PN，ON=NH，且直线OH与抛物线C在点P处的切线平行.

二、纵向探究：把特殊弦“OH”换为抛物线C的任意弦“AH”

由点M在y轴上且原点O为抛物线C的顶点，易知MO为抛物线C在点O处的切线；反之，若直线MO与抛物线C相切于点O，则点M必在y轴上.故结论1.2可改述为

结论1.3 已知抛物线C：y2=2px(p>0)，过C外一点M且平行于x轴的直线与抛物线C、弦OH(O为坐标原点)分别交于点P、N，若直线MO、MH与抛物线C分别相切于点O、H，则MP=PN，ON=NH，且直线OH与抛物线C在点P处的切线平行.

探究2 上述结论中的弦OH是以抛物线C的顶点O为一个端点的特殊弦，如果把其推广为抛物线C的任意弦AH，那么相应的结论能否成立？

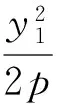
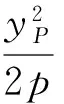
性质Ⅰ 已知抛物线C：y2=2px(p>0)，过C外一点M且平行于x轴的直线与抛物线C、弦AH分别交于点P、N，若直线MA、MH与抛物线C分别相切于点A、H，则MP=PN，AN=NH，且直线AH与抛物线C在点P处的切线平行.

特别地，当点A重合于原点O，则结论性质Ⅰ即为结论1.3.

三、横向探究：由抛物线到椭圆、双曲线的探究

著名数学教育家G·波利亚曾形象地指出：“好问题同某种蘑菇有些相像，它们都成堆地成长，找到一个以后，你应当在周围找一找，很可能附近有好几个.”

探究3 结论Ⅰ揭示了抛物线C外一点对应的切点弦与过这点且平行于抛物线C的对称轴的直线的内在联系，那么，椭圆、双曲线是否具有类似性质？

如果把结论Ⅰ 中“过点M且平行于x轴的直线”照搬到椭圆、双曲线中，显然行不通，这是因为抛物线是无心曲线，而椭圆、双曲线是有心曲线，其间似乎横亘着一道不可逾越的鸿沟.难道“过点M且平行于x轴的直线”这一关于抛物线C的条件在椭圆、双曲线中没有共同的“语言”？

重新审视这一条件，如果把无穷远点看作抛物线C的中心，那么“过点M且平行于x轴的直线”就是“点M与抛物线C的中心的连线”.真是“山穷水尽疑无路，柳暗花明又一村”！探究得以继续.

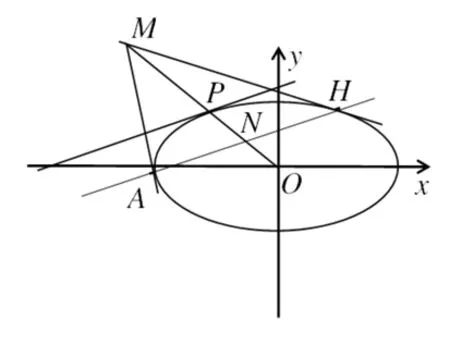
图2

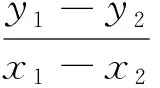
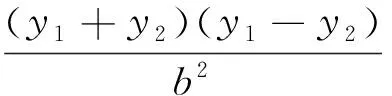
当x1=x2时，弦AH垂直于x轴，点M、P、N在x轴上，上述结论显然成立.综上可得

AH于点P、N，若直线MA、MH与椭圆C分别相切于点A、H，则AN=NH，且直线AH与椭圆C在点P处的切线平行.

类似地，容易得到

综合性质Ⅰ、Ⅱ 、Ⅲ，可得关于圆锥曲线切点弦的一个统一性质：

统一性质设AH为圆锥曲线C关于点M的切点弦，点M与曲线C的中心(对于抛物线，视无穷远点为其中心)的连线交曲线C于点P(对于双曲线，点P与切点弦AH在同一支)，则切点弦AH被该连线所平分，且切点弦AH所在的直线与曲线C在点P处的切线平行.

以上对一道高考试题进行逆向、纵向、横向探究，得到了圆锥曲线切点弦的一个统一性质.高考试题是命题者心血和智慧的结晶，是命题者留给我们的一笔宝贵“财富”.作为一线教师，要经常研究高考试题，不仅要研究试题的解法，还要深入研究试题的背景，探索隐藏在试题背后的奥秘，发掘试题的内涵，发现新的规律.只有这样，才能领会到试题的深刻背景，才能胸有成竹，高屋建瓴，才能引领学生跳出题海，做到触类旁通、举一反三.也可以引导学生对试题进行探究性学习，引导学生从试题出发，提出新的问题，探究新的结论，使学生经历在教师引导下的“问题—探究—发现”的“再创造”过程，这有助于学生初步了解数学概念和结论产生的过程，体验创造的激情，建立严谨的态度和不怕困难的科学精神；有助于学生勇于质疑和善于反思的习惯，培养学生发现、提出、解决问题的能力；有助于发展学生的创新意识和创造能力.