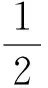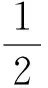从一道课本例题“证明+<2”说起
丁胜锋
广东省云浮市邓发纪念中学 (527300)
丁胜锋
广东省云浮市邓发纪念中学 (527300)

这是一道比较简单的不等式的证明,教材的意图是想通过这道题目来说明直接证明不容易,根据不等式的特点,寻求成立的充分条件,从而让学生掌握分析法证明的基本思想和操作方法.我们很多老师在实际教学中也就是按照课本上的方式处理问题,然而,学生或多或少会产生疑问,这道题除了分析方法外,难道就没有其它的方法?笔者从函数的观点来证明不等式问题.


图1

我们取x1=3,x2=7,也得到不等式的证明.
例若a,b∈R,且e 根据上述结论,我们可得到如下结论: 上述结论都是通过构造函数来解决不等式的问题,但如何恰当的构造函数,这需要根据题目本身的结构来构造,有时候我只需根据题目的原型结构来构造,有时候需要适当的变形,但具体选择那种方式来构造,这需要根据题目本身来决定.下面我们通过一个例子来多角度的说明怎样构造函数. (1)求a,b值;(2)证明:f(x)>1. 试题分析:试题(1)问不难,主要是考察导数的几何意义,函数在一点处的切线方程,只要学生对切线概念充分理解并能准确求导,即可解决第(1)问.但第(2)问中函数不等式对大多数学生设置了门槛,这个门槛主要是导函数f′(x)的零点不好求,因此需要对函数不等式做适当的变形后再构造函数来处理. e-lnx≥e(-lnx)③,当且仅当-lnx=1时等号成立. (1)若g(x)与f(x)在同一点处有相同的极值,求实数a的值; (2)若对一切x∈(0,+∞),有不等式f(x)≥2xg(x)-x2+5x-3恒成立,求实数a的取值范围; 因此关于不等式还是函数不等式的证明,我们可以通过题目本身的结构特点来构造函数,通过研究函数性质来加以证明.为我们提供了解决不等式的一个有力工具.但我们在构造函数时,又会出现构造的函数“好”“坏”直接影响解题成败,一般来说,应尽可能的构造较为简捷且很容易求出导函数零点的函数,要做到这一点,需要我们熟悉初等函数之间的组合. [1]吴振奎.中学数学证明方法[M].辽宁人民出版社,1985. [2]华中师范大学数学系.数学分析[M].高等教育出版社,2010. [3]王健.一道课本例题的多视角探究.中学数学教学参考,2016,8.