混凝土条形基础合理高度研究
杨卫忠
(郑州大学土木工程学院,河南 郑州 450001)
混凝土条形基础合理高度研究
杨卫忠
(郑州大学土木工程学院,河南 郑州 450001)
在分析《建筑地基基础设计规范》中混凝土条形基础有关规定的基础上,将基础视为悬臂梁,对基础的控制截面、承载力、允许宽高比等进行研究,研究表明,无筋条形基础应重视抗弯承载力的校核,而变截面钢筋混凝土条形基础的控制截面在最大弯矩处,考虑弯曲变形和剪切变形的影响,导出基础最大挠度计算公式,并依此建立合理基础高度的确定方法,研究成果为此类基础设计和规范修订提供参考。
混凝土; 条形基础; 控制截面; 合理高度;最大挠度
1 引言
混凝土条形基础是建筑工程中常用的形式之一,有墙下条形基础和柱下条形基础两种形式,属于扩展基础,其中,不配钢筋的条形基础也称为刚性基础。安全的基础设计需满足地基承载力和变形及基础自身的抗弯、抗剪承载力要求,基础具有足够的底面面积是保证地基承载力和变形的充要条件,而基础高度则是影响基础承载力的主要因素。现行《建筑地基基础规范》[1](以下简称基础规范)对此类基础有相应规定,对无筋扩展基础,是通过验算基础的宽高比来保证;而对底板配置钢筋的条形基础,则需验算其弯曲和剪切承载力,同时,还需满足相应的构造要求。因而,设计人员通常按经验选定基础高度,然后再进行相关的验算。但是,笔者在教学中发现条形基础设计中的某些规定不尽合理。
已有文献[2-3]仅涉及混凝土刚性条形基础的设计和钢筋混凝土条形基础的最优配筋,而且均基于已废止的规范。在近年来的注册土木工程师(岩土)继续教育必修教材[4]中,为了保证地基反力线性分布,建议基础的宽高比不超过2.5。
条形基础属于典型的混凝土受弯构件,因此,本文结合基础规范和现行混凝土结构设计规范[5](以下简称混凝土规范),对基础高度及相关问题进行研究,为此类基础设计和规范修订提供参考。在下文的研究中,是在假定基底的压应力满足地基承载力和变形的要求的前提下,仅涉及基础本身的承载力。

表1 混凝土无筋条形基础台阶宽高比的允许值
2 刚性基础的设计规定与讨论
刚性基础的允许宽高比如表1所示,表中的pk 为作用的标准组合时基础底面的平均压力值(kPa)。当混凝土基础单侧扩展范围内基础底面处的平均压力值超过300kPa时,尚应进行抗剪强度验算。
对上述规定进行分析后不难看出以下问题:
1)按混凝土规范规定,混凝土的抗拉或抗压强度与混凝土强度等级有关,只要混凝土的等级相同,其相应强度也相等。因此,对具有相同等级的混凝土基础和毛石混凝土基础,其宽高比的允许值也应一致,但是,表1中两种基础的宽高比允许值并不完全相同。
2)对基础底面处的平均压力值超过300kPa的基础,尚应进行抗剪强度验算,而基础规范的正文中并未给出具体规定,仅在条文说明中给出了验算公式,如式(1)所示。

式中:Vs——相应于作用的基本组合时的地基土平均净反力产生的沿墙(柱)边缘或变阶处的剪力设计值;
A——沿墙(柱)边缘或变阶处基础的垂直截面面积。
式(1)是利用材料力学的剪应力计算公式并取素混凝土剪切强度等于0.55ft得到的。正如基础规范所述,条文说明不具备与规范正文的同等法律效力,仅供使用者作为理解和把握规范规定的参考。
在混凝土规范附录D中给出了素混凝土的抗弯承载力计算公式,未给出素混凝土的抗剪承载力计算公式,但是,该规范的正文中则给出了对不配置箍筋和弯起钢筋的一般板类受弯构件的斜截面承载力计算规定,即
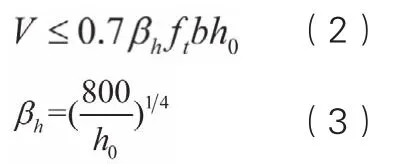
式(3)中,当h0<800mm时,取h0=800mm;当h0>2000mm时,取h0=2000mm。
进一步分析后不难看出,当素混凝土的抗拉强度也取0.55ft,截面有效高度h0取0.95倍截面高度,且不考虑截面高度影响系数时,式(2)和式(1)计算得到的抗剪承载力相等。因此,可将式(1)列入基础规范的正文,以完善规范条文。
3)表1中的允许宽高比是按pk划分,进行基础承载力计算则采用基本组合,而且是地基的净反力设计值。当刚性基础高度大于由允许宽高比确定的高度时,基础的抗弯和抗剪承载力是否就能满足,也有待进一步分析。
在开始下文的研究之前,首先讨论基础的控制截面。
3 控制截面
结构构件的设计主要是对控制截面进行承载力计算和截面验算。控制截面即是结构或构件的截面抗力与截面内力的比值为最小者处。条形基础属于混凝土受弯构件,其计算简图可视为嵌固于墙或基础梁的单向倒置悬臂梁,地基净反力就是作用在梁上的荷载,分析中可取单位长度的基础为研究对象,计算简图如图1所示。

图1 计算简图
这里,L、H分别为基础的悬挑长度和根部高度,ps,max为最大地基净反力设计值,为固定端截面的地基净反力系数。
利用力学知识,可得距离端部x处由地基净反力产生的截面剪力和弯矩分别为

下面就以刚性基础为例来推导其控制截面。由式(1),其截面的剪切承载力则为

截面剪切抗力与作用效应之比则为
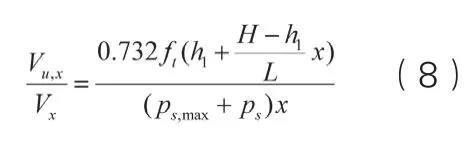
对式(8)右边对x求导,得

而截面的抗弯承载力则可利用混凝土规范附录中的公式确定,采用类似的分析方法,也可得到抗弯控制截面也在基础的固定端,即在弯矩最大的截面处。
对形如图1所示的钢筋混凝土锥形条形基础,同样也能得出:固定端截面不仅是其剪切控制截面,而且还是配筋最大的截面。因此,下面的分析就针对该截面进行。
4 刚性基础的允许宽高比
由式(1)可得满足抗剪承载力的最大地基净反力如式(9)所示。

利用混凝土规范附录D的相关公式,可得满足抗弯承载力的最大地基净反力如式(10)所示。


满足式(11)要求时,无筋混凝土条形基础只要满足抗弯承载力,其抗剪承载力一定也能满足要求,即可不必验算基础的抗剪承载力。否则,就需验算基础的抗剪承载力。表2给出几组不同应力比和基础高度时按式(11)给出的宽高比。
从上表中不难看出,宽高比均大于1.25,而且当基础高度越大(不大于1600mm)时,该限值也越大;基底应力分布越不均匀,该限值也越大。因此,在设计素混凝土条形基础时,应予以重视抗弯承载力的校核,尤其当基础高度较大且地基净反力设计值较高时。
上述结论与混凝土强度等级无关,而混凝土强度等级仅影响容许的地基净反力设计值。

表2 混凝土不需抗剪验算的宽高比
5 钢筋混凝土条形基础的允许宽高比
关于钢筋混凝土条形基础宽高比的限值,在基础规范中仅有关于轴心或偏心荷载作用下柱下矩形独立基础的规定,即不大于2.5,而墙下条形基础则无明确规定,但是,在2002版的建筑地基基础设计规范[6]中,墙下条形基础和柱下独立基础的弯矩计算采用了相同公式,而该式前提是宽高比不大于2.5。此要求可理解为保证基底应力线性分布而设置。
工程上在设计此类基础时,通常按上述要求来初选基础的根部高度。文献[4]作者又建议,在基底应力较小时,基础高度可适当放宽,而在基底应力较大时,则需加大。但是,该文并未给出具体值和定量分析。
要保证基底反力线性分布,基础就必须具有足够大的刚度,即基础的变形要小,达到所谓的刚性假定。而在混凝土框架-剪力墙结构中,为了满足楼(屋)盖在水平面内具有无限刚度的假定,通过限制剪力墙的最大间距来保证,而在该最大间距的确定时,则将楼盖视为支承于剪力墙的水平梁,通过控制其挠度与跨度的比值(即挠跨比)来实现[7]。基于此思路,也可通过控制基础的挠跨比来达到此目的。关于基础的最大挠度计算,则可采用混凝土规范的结构分析方法,截面刚度采用弹性刚度,即弹性模量取混凝土的弹性模量,截面模量按实际截面尺寸计算,不考虑内部钢筋的影响。
对图1所示的悬臂梁,考虑弯曲和剪切变形的最大挠度可利用结构力学公式计算,即

进一步计算和分析可得具体表达式为

式中ξ为变截面时的挠度修正系数,一般在1.1~2之间,可近似按式(14)计算。当地基反力均匀分布时,取η=1。

这里,h1是条形基础的端部高度。
由于条形基础属于悬臂构件,跨度取2倍的悬挑长度,当给定容许的挠跨比后,即可求得允许宽高比的具体值,涉及到的超越方程可利用数值分析中的牛顿公式求解,当取其一次近似解即可获得满意的精度,初始宽高比可取2,具体求解公式如下:

关于基础的容许挠跨比[f /2L],笔者建议可按1/8000取值,此限值大致相当于普通混凝土构件挠跨比的1/10,考虑了变形计算时的荷载为准永久组合,而且还考虑了荷载长期效应的影响。因此,按式(15)计算时,可直接采用基本组合时的基底净反力。
6 钢筋混凝土条形基础的合理高度
在已知基础底面宽度(即悬挑长度也已知)、和地基净反力后,钢筋混凝土条形基础设计的关键是确定其根部高度。根据上述分析,满足抗剪承载力和刚性假定要求的最小基础高度可总结为如下关系式:
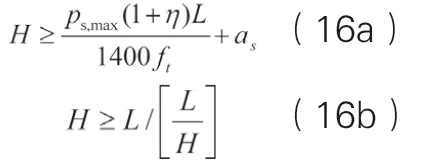
若最大基础高度取最大弯矩作用下截面最小配筋率(按基础规范取为0.15%)时对应的高度,利用抗弯承载力计算公式并适当简化,即

若基础高度超过式(17)限值,则直接按最小配筋率配筋。
在确定了基础根部高度后,根据基础外形的构造要求来确定其他尺寸,即基础的端部高度不宜小于200mm,阶梯形基础的每阶高度宜为300mm~500mm,而锥形基础的坡度不宜大于1:3。
下面结合文献[4]的某工程实例给出具体计算步骤,基础剖面尺寸及基底净反力如图2。
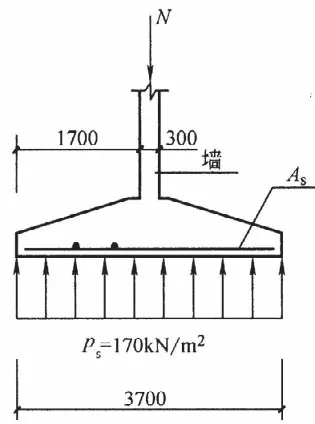
图2 剖面尺寸及地基净反力
若采用C30混凝土和HRB400级钢筋,h1=300mm,则有:Ec=30000N/mm2,ft=1.43N/mm2,fc=14.3N/mm2,fy=360N/mm2,L=1700mm。基底设置C15混凝土垫层,as=50mm。
由式(1 6 a),解得:H≥339mm;由式(15)、(16b)解得:H≥654mm;由式(17)解得:H≤726mm。综合考虑后,可取H=700mm。此结果与该文献结果一致。
进一步考虑地基净反力较大或较小的情况,而其他条件不变。
情况I:地基净反力设计值改为255kN/m2,可解得:H≥483mm, H≥784mm和H≤876mm。因此,可取H=800mm。
情况II:地基净反力设计值为105kN/m2,可解得:H≥228mm, H≥528mm和H≤580mm。因此,可取H=550mm。
上述3种情况,按0.4倍挑长得到的基础根部高度均为680mm,而本文采用考虑基础刚度的截面高度确定法得到的结果则反映了地基净反力、材料等因素的影响,结果更为合理,从而也避免了基础高度确定的经验性。
对条形基础这样的单筋矩形截面受弯构件,且抗剪承载力较为富裕,内力臂系数可偏于安全地取为0.95,因此,基础底板需配钢筋的面积计算式如下:

上式结果较现行基础规范结果则更为经济。
7 结论
假定地基反力为线性分布,且满足地基承载力和变形要求,通过对混凝土条形基础的承载力分析,主要研究结论总结如下:(1)满足基础规范的允许宽高比,部分基础的抗弯承载力验算比抗剪承载力验算更重要。(2)变截面条形基础底板的控制截面可取为弯矩最大处。(3)考虑弯曲和剪切变形,建议变截面条形基础最大挠度计算公式,并依此确定基础的允许宽高比和合理高度,而基础的允许挠跨比可取1/8000。
[1]中华人民共和国住房和城乡建设部.建筑地基基础设计规范(GB500007-2011)[S].北京:中国建筑工业出版社,2011.
[2]宋相道,李华亭.刚性基础设计中的一些问题[J].建筑结构,2004,34(4):51~53.
[3]王常清,霍达.钢筋混凝土条形基础的最优化设计[OL].http:/www.cnki.net.
[4]朱炳寅,娄宇,杨琦.地基基础设计方法及实例[M].第2版.北京:中国建筑工业出版社,2013.
[5]中华人民共和国住房和城乡建设部.混凝土结构设计规范(GB500010-2010)[S].北京:中国建筑工业出版社,2010.
[6]中华人民共和国建设部.建筑地基基础设计规范(GB500007-2002)[S].北京:中国建筑工业出版社,2002.
[7]程文瀼主编.混凝土结构设计[M].武汉:武汉大学出版社,2006.
2017-08-23

