变截面悬臂梁最大挠度简化计算

康兰兰

（河南建筑职业技术学院，河南 郑州 450064）

变截面悬臂梁最大挠度简化计算

康兰兰

（河南建筑职业技术学院，河南 郑州 450064）

考虑梁的弯曲变形和剪切变形，利用单位荷载法得到了等宽、截面高度线性变化的矩形截面悬臂梁在均布和集中荷载作用下的最大挠度计算公式，定义该挠度与按根部高度的等截面梁最大挠度之比为挠度增大系数，构件两端的截面模量之比是影响挠度增大的最主要因素，荷载分布形式也有一定影响，通过参数分析，得到其简化表达式，计算结果表明，所建议的公式具有很高的精度且计算简便。

悬臂梁； 最大挠度； 变截面

0 引言

对承受横向荷载作用的构件而言，弯矩和剪力是其主要内力，采用变截面则易于充分发挥材料强度，节约了材料，因此，在土木工程中变截面构件较为常见，如挑梁、门式刚架的梁和柱、锥形扩展基础等。相对等截面梁而言，变截面梁的挠度较大，过大的变形影响结构的正常使用。一般的力学教材或结构设计手册都有等截面构件在常用荷载下的挠度计算公式，而变截面梁由于截面特性是位置的变量，当采用积分法计算其挠度时，其显式表达一般较复杂甚至无法求解。因此，变截面构件的挠度，常采用近似方法计算。其中，共轭梁法[1]需计算虚梁内力图的合力及位置，相应地，计算也较为复杂；等效刚度法[2]将构件分若干段后，利用最大挠度相等得到其等效刚度，再利用等截面梁的挠度计算公式得到具体挠度，该法的计算工作量较大。而在工程实践中，构件的截面变化往往具有某些规律，如宽度相同仅高度线性变化的矩形截面。因此，有必要研究一种易于求解此类截面构件最大挠度而又具有较高精度的实用方法。

本文利用经典结构力学中的单位荷载法，考虑构件的弯曲和剪切变形，通过合理的积分计算，得到高度线性变化的悬臂构件在均布和集中荷载作用下最大挠度计算公式，进一步通过参数研究，得到简化的实用计算公式，为此类构件的挠度计算提供了简单实用的计算方法。

1 构件参数和最大挠度计算原理

1.1 构件参数

以矩形截面的悬臂梁为例，截面宽度为b，梁悬挑长度为L，端部和根部高度分别为h1和h，如图1所示。

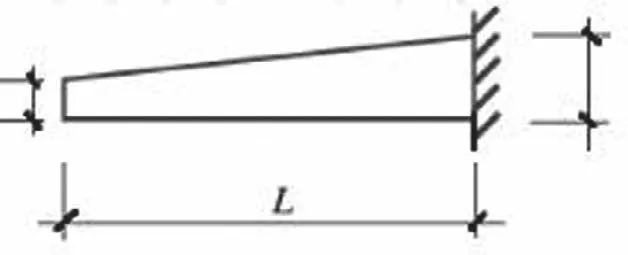
图1 构件参数

构件端部和根部的截面面积和截面模量分别如下：

端部截面，

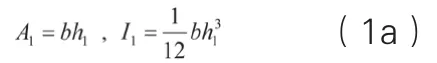
根部截面，

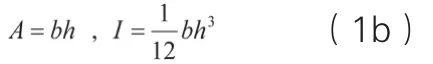
由于截面高度线性变化，则构件的高度变化率为

1.2 最大挠度计算原理

对图1所示的悬臂构件，最大挠度发生在自由端，可利用单位荷载法求出。即在端部施加与荷载引起挠度方向一致的单位力，分别计算荷载和单位力引起的在截面位置x处的弯矩和剪力，考虑了弯曲和剪切变形的最大挠度即为

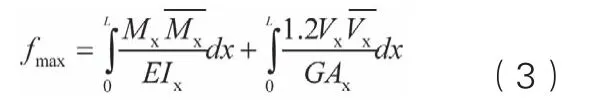
式中

1.2 ——考虑了截面上剪应力的不均匀系数。

显然，式（3）中的第1项即为弯曲变形产生的挠度，第2项则为剪切变形产生的挠度。

2 最大挠度的理论解

2.1 集中荷载作用

当端部作用集中力F时，截面位置坐标原点定义在截面积面积为0处，该点离端部的距离a即为

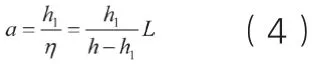
相应地，截面位置x处的截面特性和内力如下：

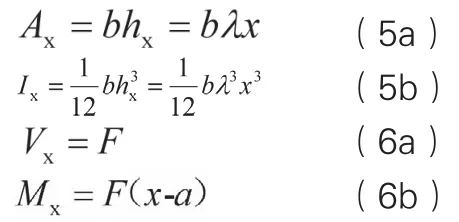
将式（5）～（7）代入式（3），同时，积分区间变为[a ， a+L]，通过积分得最大挠度为

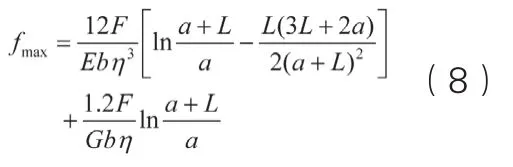
2.2 均布荷载作用

当梁上作用均布荷载p时，采用与集中荷载相同的处理方法，仅荷载引起的截面弯矩和剪力不同，其余参数不变。利用平衡条件可得截面位置x处的内力如式（9）所示。

同样利用式（3），即得最大挠度为

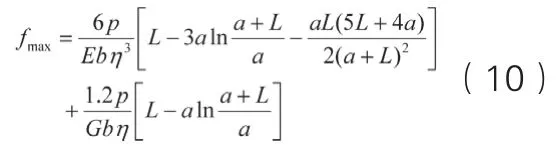
3 最大挠度的简化解

若截面高度等于根部截面高度的等截面悬臂梁在荷载作用下的最大挠度记为，而变截面梁最大挠度可表达为此挠度与挠度增大系数ξ的乘积，即

端部集中力作用时，

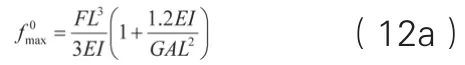
梁上均布力作用时，

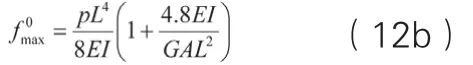
将式（8）、（10）和（12）分别代入式（11），即得两种典型荷载作用时的挠度增大系数。不难看出，所得的挠度增大系数甚为复杂而难于应用，可通过数值分析方法得到其简化表达式。

由挠度增大系数与F、E、G和b的无关，而与ln（I/I1）相关。为了建立其关系式，构件参数分别取：h1=50、100、200、400、500（mm）；L=500、1000、1500、2000、2500、3000（mm）；η=0.01、0.05、0.10、0.15、0.2、0.25、0.30、0.35、0.40、0.50，通过分析可得具体关系式如下：

集中荷载作用，

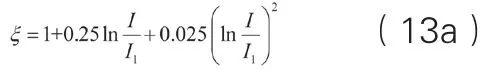
均布荷载作用，

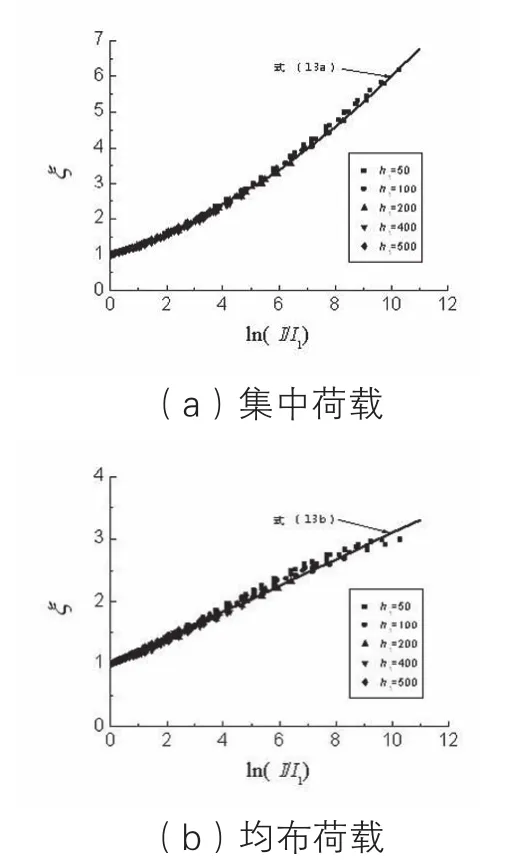
图2 简化解与理论解的比较

图2给出了理论值与简化计算结果的比较。仔细研究后不难看出，简化解具有较高的精度，能满足工程要求。

利用式（1），式（13）可相应地转换为式（14），即

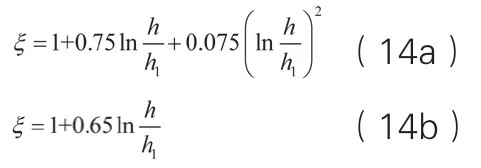
若变截面梁为工程上的混凝土梁，则有G=0.4E，式（12）可进一步简化。同样，对跨高比（L/h）不大的浅梁和短梁，剪力引起的梁挠度不能忽略。

尽管上述导出的挠度增大系数是基于矩形截面梁的分析，只要梁的截面高度是线性变化，式（13）的结果同样也具有很高的精度。

4 算例

某悬挑长度为L=2100mm的变截面挑梁，梁上作用均布线荷载为p=20kN/m。已知：梁端部截面尺寸为200mm×200mm，根部截面尺寸为200mm×450mm，材料的弹性模量E和剪切变形模量G分别为30GPa和12GPa，试确定其最大挠度。

由于该变截面梁属于均布荷载情况，由式（10）理论公式计算得最大挠度为1.7077mm，而按式（11）得最大挠度为1.527×1.116=1.7041mm。二者误差为0.2%。

由此可以看出，本文简化方法可以利用一般等截面的计算结果，不仅计算简单，而且具有较好的计算精度，能满足工程设计要求。

[1]龙驭球，包世华，支秉琛.结构力学（上册）[M].北京：高等教育出版社，1994.

[2]朱皓明，高轩能，沈剑波.变截面悬臂构件挠度计算的等效柱法[J].井冈山大学学报（自然科学版），2010，3l（4）：71-75.

2017-08-23