初中数学几何题解题技巧

安徽省芜湖市无为县福渡初中 吴子赟

初中数学几何题解题技巧

安徽省芜湖市无为县福渡初中 吴子赟

几何题在初中数学内容中占据着十分重要的地位，是初中数学教学重难点之一。由于几何题强大的灵活性、广泛的知识点及其逻辑的严谨性，让很多学生往往都无从下手。但如果能掌握几何题的解题技巧，那么解决这类题目就可谓轻而易举了。本文就初中数学几何题解题技巧做了几点阐述。

初中数学；几何题；解题技巧；辅助线；实际应用

在初中数学几何题当中，有许多解题技巧可以用来帮助我们得分。在这些解题方法当中，最典型的三点就是归纳总结常见题型和常见解法、灵活掌握并运用辅助线以及总结特殊题型下的常见辅助线。若能熟练掌握这些解题技巧，不仅能让解题速度加倍，还能做出一定程度的难题。解题技巧无论在初中数学的哪一种题型中，都具有十分重要的意义，在几何题型中，其地位更加重要。对几何题感到头疼烦恼的同学，看了本文定能有所帮助。作为一名初中数学老师，对于几点典型的几何题解题技巧，下面做一个更加详细的阐述。

一、归纳总结常见题型和常见解法

在初中数学考卷当中，几何题的题型其实是大有规律可循的。针对这些不同类型的几何题，掌握其对应的解法，即可让几何成绩上一层楼。在初中几何题中，常见的题型并不是很多，学会归纳总结常见题型的解法，对解答几何题大有帮助。在初中几何题中，证明题是最常见的题型，而在证明题当中，又大多以线段及角的关系作为考查点，其通常包括线段与角的相等关系证明、线段与角的和差关系的证明。对于这一类题型，解题思路常常是利用“全等三角形”、“等角对等边”、“比例线段”等知识点，此外，常见的还有利用中间量作为过渡等等。“三角形全等”的知识点是考查最多的内容，全等三角形的判断包括了“角边角”、“角角边”、“边角边”等方法。学会掌握细致的相关知识点，在解几何题的过程中就能够派上用场，为解几何题添上一臂之力。

二、灵活掌握并运用辅助线

辅助线是初中数学几何题的解题要素，学会灵活运用辅助线是每一个学生必不可少的技能，这是除掌握题型解法外更值得老师和学生关注的问题。当一些几何题无法直接解出或者直解遇到障碍时，添加辅助线往往会让人有柳暗花明之感。例如：如图，在△ABC中，∠C=90°，AB=AC，AD=AB，AE=CF，请证明：DE=DF。

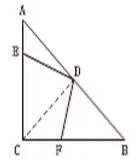
通过分析可知，在图中并不能直接找到线段相等的依据，也无法找到两个全等的三角形。学生常常会因此陷入困境。但是如果再仔细观察图形，并在脑中产生作辅助线的自觉性，便不难发现，可以通过连接CD作一条辅助线，形成两个全等的三角形AED与三角形CDF。其证明过程如下：如图，连接CD。因为∠C=90°，AC=BC，所以三角形ABC为等腰直角三角形，所以△ACD≌△BCD，且也为等腰直角三角形，所以CD=AD，∠CAB=∠BCD=45°。又因为AE=CF，所以△AED≌△CDF，则DE=DF得证。本题仅做例子以说明辅助线的重要性，学生在解几何题时应该时刻注意对辅助线的应用方法有所掌握。此外，还有很多几何中的基本知识点要烂熟于心，在本题中，就涉及等腰直角三角形两边相等的基本知识点。在三角形中，中线或角平分线常常是辅助线，而在等腰直角三角形中，斜边上的中线则往往就是辅助线。在梯形中，通过平移梯形中的某腰或者做某条线的垂直线，将梯形转变为平行四边形来解题，也是常见的辅助线添加方法。在几何题中，辅助线作用颇多，学生一定要加以重视。

三、掌握实际问题中的几何应用技巧

几何题的考查形式可以是直接的条件描述，也可以通过实际应用题的形式进行表述。在实际应用题中，出题者要求考生从实际问题中构建出几何模型，将应用题转换成几何题进行解答。实际应用题通过生活中的实例来考查学生对几何知识点的掌握程度，另一方面，这类题型也加强了学生运用所学知识解决生活问题的能力，将理论运用到实践当中去。应用题还能在一定程度上加强学生的思维能力，让学生对问题进行抽象概括、综合分析以及推理证明的能力得到提高。例如，公路MN与公路PQ相交于点P，且∠QPN=30°，在线段PQ上距P点120米处有一学校A，一拖拉机在MN公路上延MN方向行驶，其噪音在距其90米内均会受到影响，请问A学校是否会受到拖拉机噪音的影响？在此题中，应该根据题意在纸上做出示意图，不难发现，以A点为圆心，以90米为半径做圆，只要拖拉机行驶到圆内，则学校就会受影响。通过图形不难发现，从A点作MN的垂线AD，只要AD＜90米就会受影响。通过辅助线构成三角形APD，且∠PAN=30°，所以AD=60米，小于90米，所以学校会受影响。本例说明了应用题是如何构建几何模型的，在应用题中，一般只要构建出了几何模型，其解题方法并不难。

初中数学几何题说难则难，说不难亦不难。只要教会学生掌握几何题的三大解题技巧，并熟练几何基本知识点，那么大多数初中几何题都能得到解决。

[1]王磊．初中几何题的解题思路分析[J]语数外学习（初中版·中旬刊），2013（5）．

[2]李秀丽．初中数学教学中几何解题思路分析[J]中小学教学研究，2013（4）．

[3]王春霞．几何解题技巧及思维能力培养[J]中学生数理化(教与学 )，2013（6）．