必经节点集约束型无环最短路径算法研究
李 东,严 义,王丹东,王 强
(杭州电子科技大学计算机学院,浙江 杭州 310018)
必经节点集约束型无环最短路径算法研究
李 东,严 义,王丹东,王 强
(杭州电子科技大学计算机学院,浙江 杭州 310018)
基于遗传算法和Dijkstra算法,提出了解决必经点集约束型无环最短路径问题的方法.将研究问题分解为只含源点、目的节点和必经节点集的非对称旅行商问题和消除环路问题.首先利用遗传算法求解非对称旅行商问题得到最优必经点序列.但求解得到的最优必经点序列组成的路径是有环路径,为解决环路问题,设计了分段Dijkstra破环策略.通过实验分析验证了算法是有效可行的,相对于传统方法,在时间效率上有较大的提升.
必经节点集约束;遗传算法;Dijkstra;最短路径;消除环路
0 引 言
随着电子商务、网络通信等不断发展,对约束型路径规划,特别是必经节点集约束型路径规划的需求日益增加.对于最短路径问题的研究已非常普遍,其中对旅行商问题(Traveling Salesman Problem,TSP)的研究最为广泛,可采用蚁群算法、遗传算法、LKH算法等来解决TSP问题[1-3],但TSP问题只是求解从源点出发经过所有节点最终回到源点的最短路径问题.Adam N.L.等[4]提出了用于解决子旅行商问题(Subset Traveling Salesman Problem, STSP)的方法,STSP问题要求路径需访问指定节点集,但目标路径可以存在环路.冯琳耀等[5]提出通过几何代数算法解决经过特定节点且路径节点数最少的问题,该算法关注点在于经过的节点数目少而不是经过的路径最短问题,且只适用于无向图,对于有向图最短路问题无法适用.黄书力等[6]基于Dijkstra算法提出了求解源点到目的节点经过指定中间节点集的最短路径问题,该算法求得的路径是一条有环路径,且只能用于求解无向无权网络.在网络规模小且必经点数目极少的情况下,可使用回溯法和动态规划等来解决研究问题[7],然而随着网络规模和必经节点集规模的增加,回溯法和动态规划等精确算法的时间复杂度成指数级增加,在指定时间内根本无法解决此类问题.
针对此类问题,本文将复杂的问题分解为非对称旅行商问题(Asymmetric Travelling Salesman Problem,ATSP)和消除环路问题,通过遗传算法和Dijkstra分段策略分别求解,并对问题进行了数学抽象和算法实现.
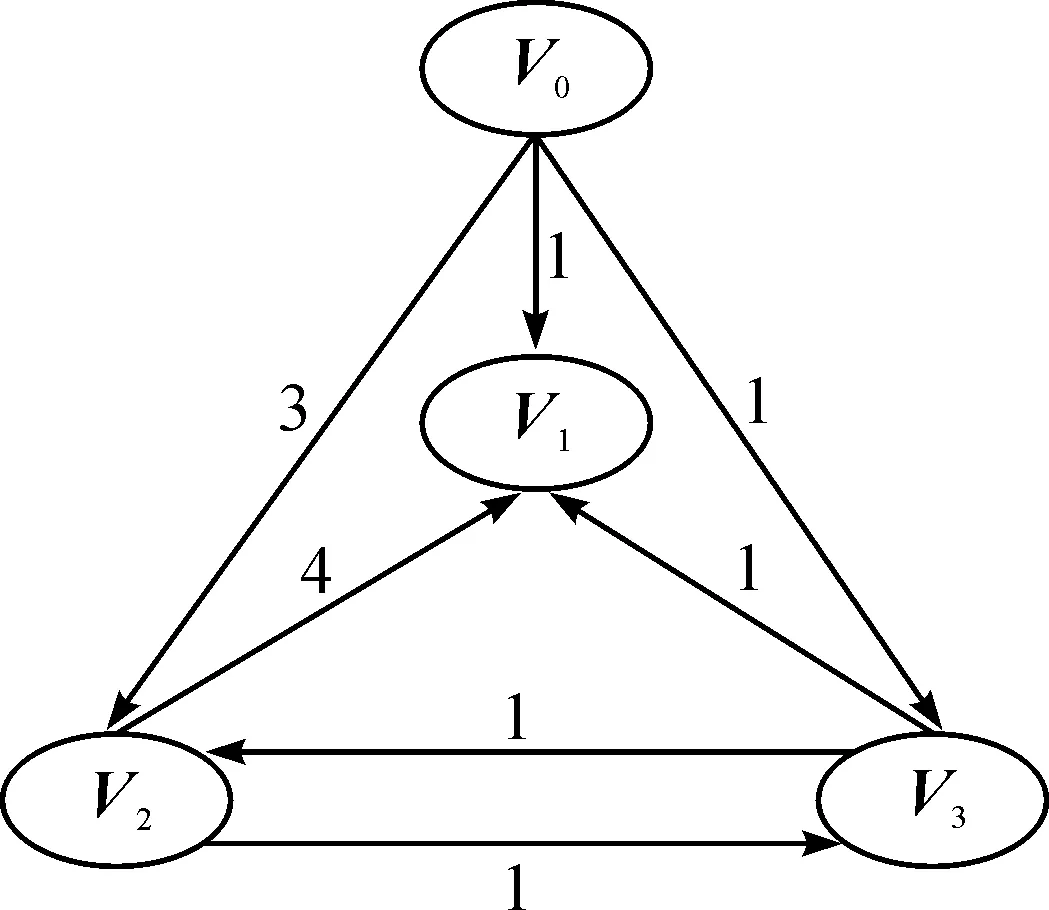
图1 必经点集约束型无环最短路径问题示例图
1 问题描述与定义
1.1 问题描述
本文研究的问题是在带权有向网络中,求解从源节点经过指定节点集到目的节点的最短路径,且路径中无环路,问题的实例网络如图1所示.源点V0到目的节点V1的最短路径是V0-V1,权值和为1,经过必经节点集{V2,V3}且无环的最短路径为V0-V2-V3-V1,权值和为5.V0-V3-V2-V3-V1这条路径权值和虽然较小(权值和为4),但这条路径存在回路,不满足问题要求.
1.2 问题定义
给定一个带权有向图G(V,E),V={v1,v2,…,vn}为顶点集,E={e1,e2,…,en}为有向边集,每条有向边的权重为wij.对于给定源点s和目的节点t,以及必经节点集V′⊆V-{s,t},找出从s到t的无环最短路径P,使得P通过V′中所有节点,简称为(s-V′-t)最短路问题.设x∈(0,1),若弧(i,j)在路径P中,xij=1,否则xij=0,则问题的数学模型是:
求解
(1)
(2)
(3)
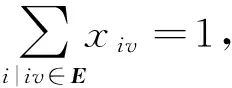
(4)
Vp∩V′=V′
(5)
其中,约束(2)和(3)定义了一条源点到目的节点t的路径;约束(4)是避免路径P中出现环路;约束(5)要求路径P经过必经节点集V′中的每一个节点.
2 算法设计与实现
2.1 算法总体设计
首先将原网络转换为只含源点、目的节点和必经节点集的子网络,子网络中节点间的权重为原网络中节点间的最短路径长度,然后将(s-V′-t)最短路问题分解为从源点经过所有子网络节点到达目的节点的最短路径问题,这其实是一个特殊的ATSP问题,可以利用改进的遗传算法求解此类ATSP问题得到最优必经点序列,最后利用Dijkstra分段破环策略求对最优必经点序列路径进行破环操作.
2.2 简化网络结构
定义1在一个网络中,若一个节点的出度之和为0或者入度之和为0,那么该节点称为边缘节点.
定义2在一个网络中,若一个节点的出度之和及入度之和均为0,那么该节点称为孤立节点.
简化网络结构就是从原网络中删除目标路径中必然不包含的节点.若某必经节点为孤立或边缘节点,那么目标路径是不存在的.若一个节点为孤立节点或者边缘节点,该节点必然不会出现在目标路径中,则可以删除此类节点以及以此类节点为起点或终点的弧.通过删除孤立节点和边缘节点,降低网络规模,提高算法的执行效率.
2.3 改进遗传算法求解最优必经点序列
最优必经点序列是特殊的ATSP问题,遗传算法是基于“适者生存”的一种高度并行、随机和自适应的优化算法,具备较好的全局搜索能力,能够快速搜索出解空间中的全体解,而不会陷入局部极值[8],故可以用来求解ATSP问题.在实际应用中,遗传算法的局部搜索能力较差,以致于单纯的遗传算法十分费时,在迭代后期搜索效率较低,为此本文通过改进遗传算法的选择和变异操作,大大提高了遗传算法的收敛速度和求值能力.
遗传算法求解实际问题主要步骤是:问题的描述和编码、产生初始种群、构造适应度函数、选择、交叉、变异算子的选取等.下面将根据(s-V′-t)最短路问题进行逐一讨论.
2.3.1 问题的描述和编码
遗传算法求解TSP问题常见的编码方式有顺序编码、近邻编码、矩阵编码、路径编码等[9],由于路径编码是最符合本文问题逻辑的编码方式,经过每一个必经点且不会产生回路,所以本文采用路径编码,源点为起始编码,目的节点为终止编码,中间编码为必经点序列.如编码0231表示图1中V0节点依次经过V2,V3到达V1的一条路径.
2.3.2 初始种群的产生
由于起始编码和终止编码是确定的,所以初始种群的产生只关注必经节点集的排列顺序.必经节点序列的编码方式采用随机方式和启发式方式,其中90%的初始种群通过随机产生,10%通过启发式产生,结合A*算法[10],启发式方式是从源点开始,距离上一编码和终止编码之和最近的点作为该条染色体当前位编码.混合产生方法能加快算法的收敛速度.
2.3.3 适应度函数的构造
适应度函数的构造是遗传算法的重要组成部分,直接影响遗传算法的收敛速度和成败.最优必经点序列不仅要求路径长度短而且要求序列中的环路数量少,为此本文在设计适应度函数时,充分考虑了这两方面的需求.设染色体路径长度为Rd,路径中出现的环路数量为n,每个环路惩罚权值为a,经过反复验证,a取网络节点数量与网络中边的最大权重的乘积效果最优.当n越小,路径长度Rd越小,越容易遗传到下一代,所以适应度函数取路径长度和环路惩罚值之和的倒数,即:
(6)
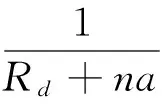
(7)
适应度函数的设计加入了环路惩罚机制,降低必经点优秀序列中存在环的可能性,可以大大降低破环的难度,提升了算法的效率和准确性.
2.3.4 选择操作
选择操作是从种群中选择优胜染色体,常用策略有轮盘赌选择和锦标赛选择等[11].本文为了加快遗传算法的收敛速度,选用轮盘赌选择和锦标赛选择混合的策略,对适应度值进行排序得到一定比例的前N个最优染色体直接进入下一代,剩余染色体通过轮盘赌方式选择.
2.3.5 交叉策略
本文采用交叉策略是最常见的路径交叉策略,把一对父代部分染色体片段进行交换重组生成一对新的染色体过程,这种交叉策略理论已经十分成熟,本文不作详细论述.
2.3.6 变异策略
互换变异是常用的路径变异策略,将一条染色体中的两个基因片段互换.反转变异是另一种常用的路径变异策略,将染色体片段进行反转.但是这两种变异策略的搜索邻域范围都比较小,为克服遗传算法局部搜索能力差的缺点,本文构造了大邻域搜索变异策略(Bigger Neighborhood Search Mutation Strategy, BNSMS).BNSMS策略的主要思想如下:
BNSMS策略主要结合反转变异和交换变异,遗传算法进行第一次迭代时采用变邻域反转变异策略,可以选择出接近最优值的一条路径,之后各代均采用交换变异策略,这样可以有效的跳出局部最优.变邻域反转变异策略步骤如下:
1)获取交叉后的当前最优解P′(s-b1-…-bi-…-bj-…-bn-t);
2)因为是有向网络,故通过染色体片段反转,扩大变异的搜索邻域,保持种群的多样性,基于这个思路,提出了循环反转方案进一步扩大搜索邻域,伪代码如下:
BNSMS变异策略不仅可以防止早熟,跳出局部最优,还具备较强的局部搜索能力,同时可以扩大搜索邻域,从而加快收敛速度.
2.4 解决环路问题
通过改进遗传算法求得优秀必经点序列,虽然在遗传算法中加入了降低环路数量处理,但依然不能保证路径中没有环路,若存在环路,需要进一步破环处理.基于Dijkstra算法,本文提出了一重Dijkstra破环策略和二重Dijkstra破环策略.一重Dijkstra破环策略如下:
1)对路径P′(s-b1-…-bi-…-bj-…-bn-t)进行分段破环求出当前段最优路径,保存到P中,并将这段路径中的节点禁忌,不允许出现在之后的路径中.如通过分段Dijkstra算法依次求(s-b1)、(b1-b2)…(bn-t)之间的最短路径,若(s-b1)中求得的路径为(s-v1-v2-b1),则节点{s,v1,v2}需要禁忌,再分段Dijkstra求(b1-b2)时,{s,v1,v2}不会出现在此时(b1-b2)的最短路径中.
2)若某段优秀序列(bi-bi+1)中进行分段破环时无法求出通路,说明(bi-bi+1)中的必走节点被前面求出的最短路径序列占用,需要分段打开之前的禁忌路径节点,再对当前序列对和打开序列对这两组序列对进行先后分段破环,若两段同时能够连通,说明这两组序列对之间的路径均为较好路径.若不能够同时连通,则说明当前序列对被占用的必走节点集不在被打开序列中,再依次向前打开释放禁忌节点.
二重破环是在一重破环失败的前提下使用的,说明两个不能连通的必经点之间的路径必走节点集被前面的两个或两个以上的必经点序列对占用.主要思想和一重破环类似,最大的区别是一重破环每次打开一组必经点序列对,而两重破环是同时打开两组必经点序列对.若一重破环和二重破环都无法成功破环,说明遗传算法求得的优秀必经点序列不是最优序列,此时将本次的优秀序列作为初始种群中的一条染色体继续寻优.根据算法的特点,无论是遗传算法求解必经点最优序列还是环路破环策略,其时间复杂度主要与必经点集规模有关,算法的总体流程如图2所示.
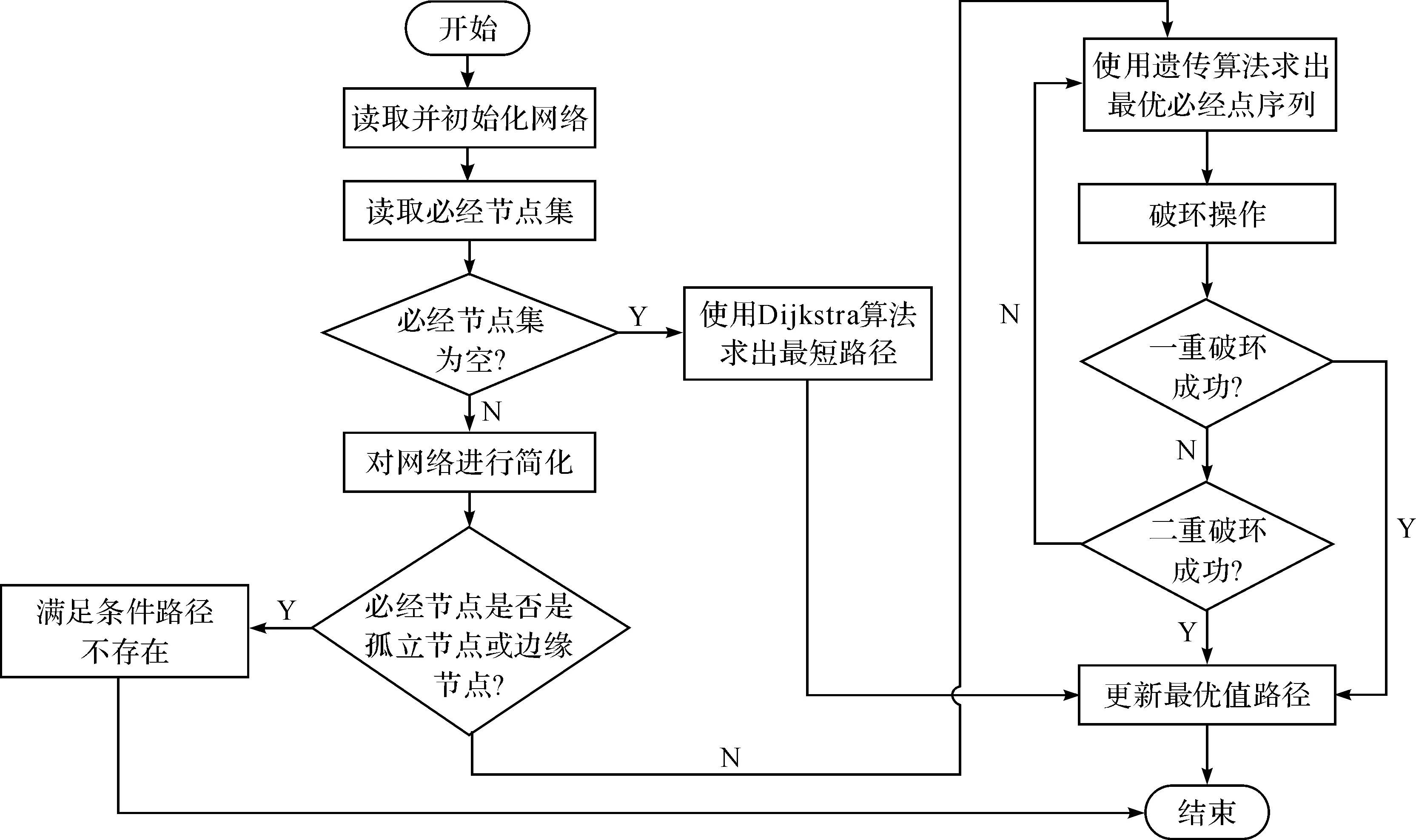
图2 算法流程
3 实验结果及分析
本文的实验环境是Ubuntu系统,2.2 GHz i3 CPU,算法采用C++语言实现.网络实例和必经节点集均是随机生成.网络实例的源点为1,目的节点为节点数目|V|.
3.1 验证算法的正确性
网络实例如图3所示,具有36个节点,弧段数为108,必经节点集规模为6,记为G(36,6).求解从源点1经必经节点集{18,19,24,28,29,35}到达目的节点36的最短路径.根据2.2节描述的简化网络方法删除边缘节点17,6,8,25以及删除以源节点1为终点的弧和以目的节点36为起点的弧,简化网络如图4所示.
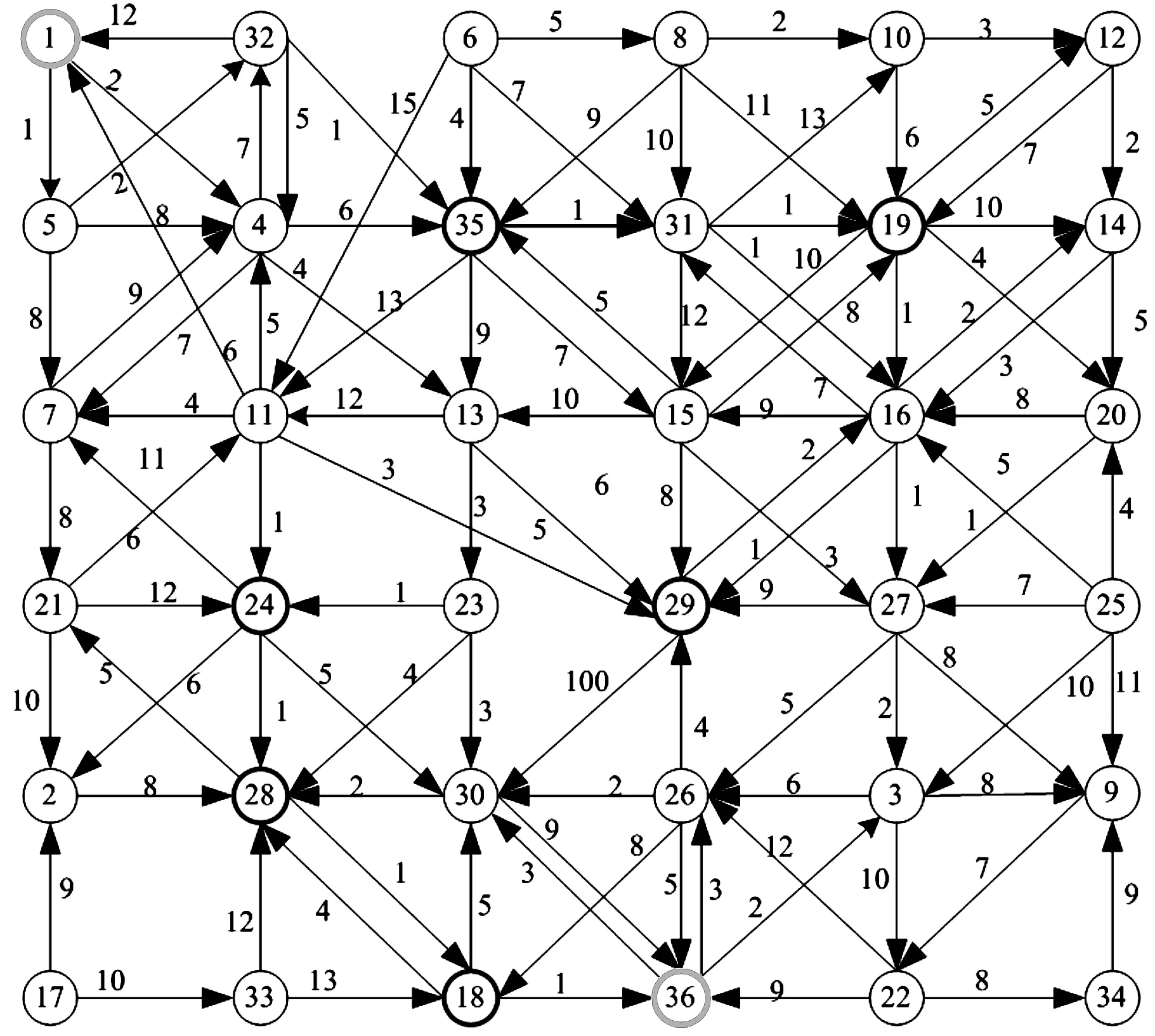
图3 G(36,6)实例网络
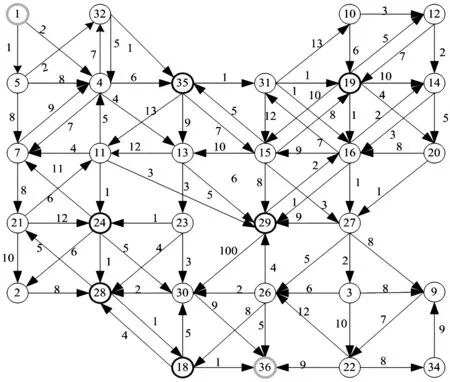
图4 G(36,6)简化网络
通过改进遗传算法求得的必经点最优序列为1-35-19-29-24-28-18-36,但这条最优序列组成的路径是有环路径,如表1所示,必经点29到必经点24之间的路径必须要经过节点16,而节点16已经出现在必经点19到必经点29的路径中,这样就形成环路,导致节点29与节点24之间在无环情况下无法连通,这时需要将节点19,16从禁忌节点集中删除,先后通过分段破环策略计算节点29到节点24和节点19到节点29之间的最短路径,使得两段路径能够同时连通.

表1 小规模网络有环路径
小规模网络破环过程如表2所示,最优不成环路径序列为1-5-32-35-31-19-14-20-27-26-29-15-13-23-24-28-18-36,路径权值和32,是网络G(36,6)中从源点1经过必经节点集到节点25的最短路径耗时10 ms,实验结果表明本文提出的算法是有效可行的.

表2 小规模网络破环过程
3.2 算法效率分析
图5展示的是必经点集规模大小为48的情况下,随着网络规模的增大,算法执行时间的变化情况,图6展示的是网络规模为2 000时,随着必经点集规模的增大,算法的执行时间变化情况.可以发现,在必经点集规模一定的情况下,算法执行时间变化较为平缓,但在网络规模一定的情况下,当必经节点集规模超出98时,随着必经节点集规模的增大,算法执行时间急剧增加,充分体现了本文算法的时间复杂度主要与必经节点集规模有关,对于大规模网络而必经点相对少的情况下,本文算法是十分高效可行的.
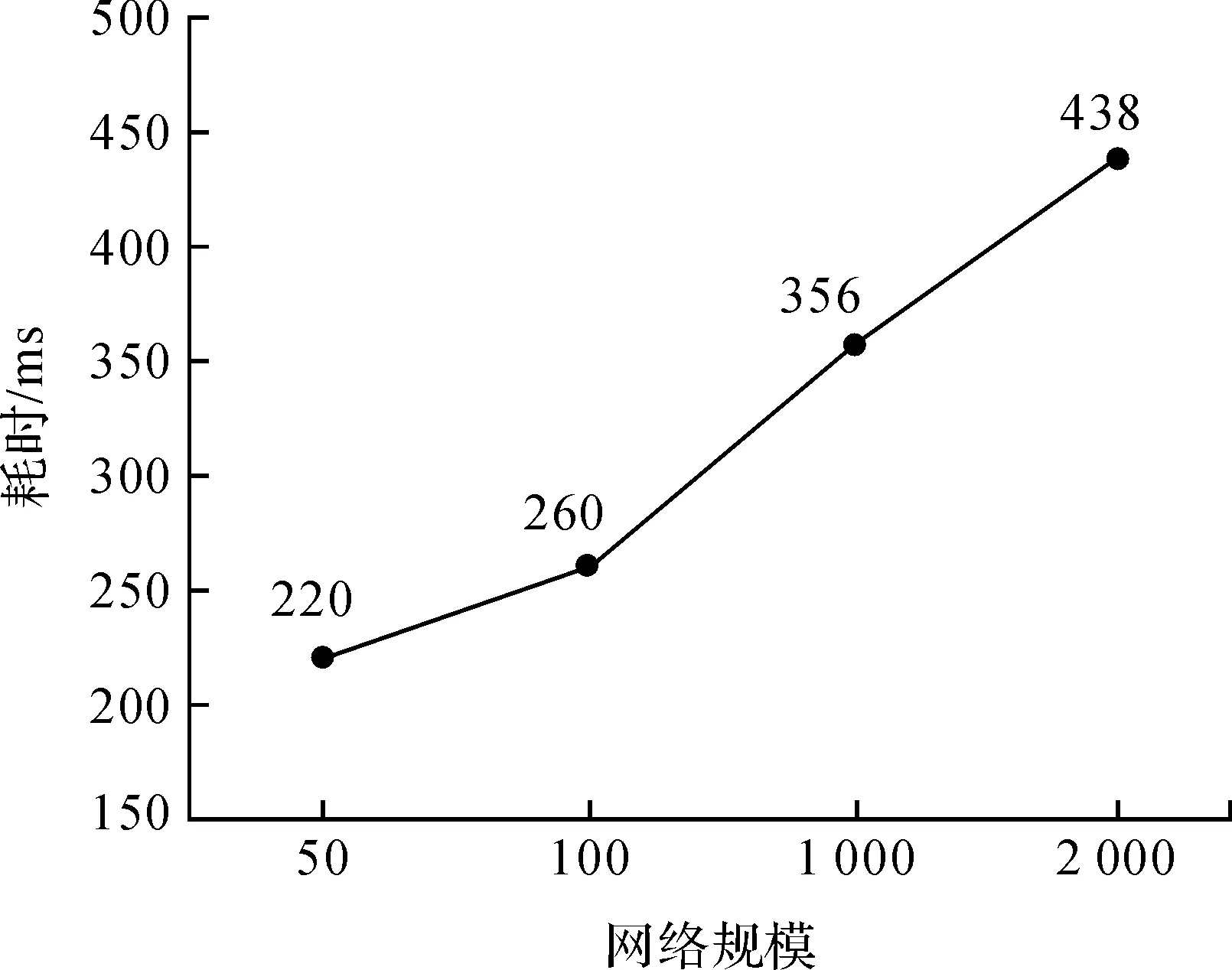
图5 指定必经节点集规模算法时间
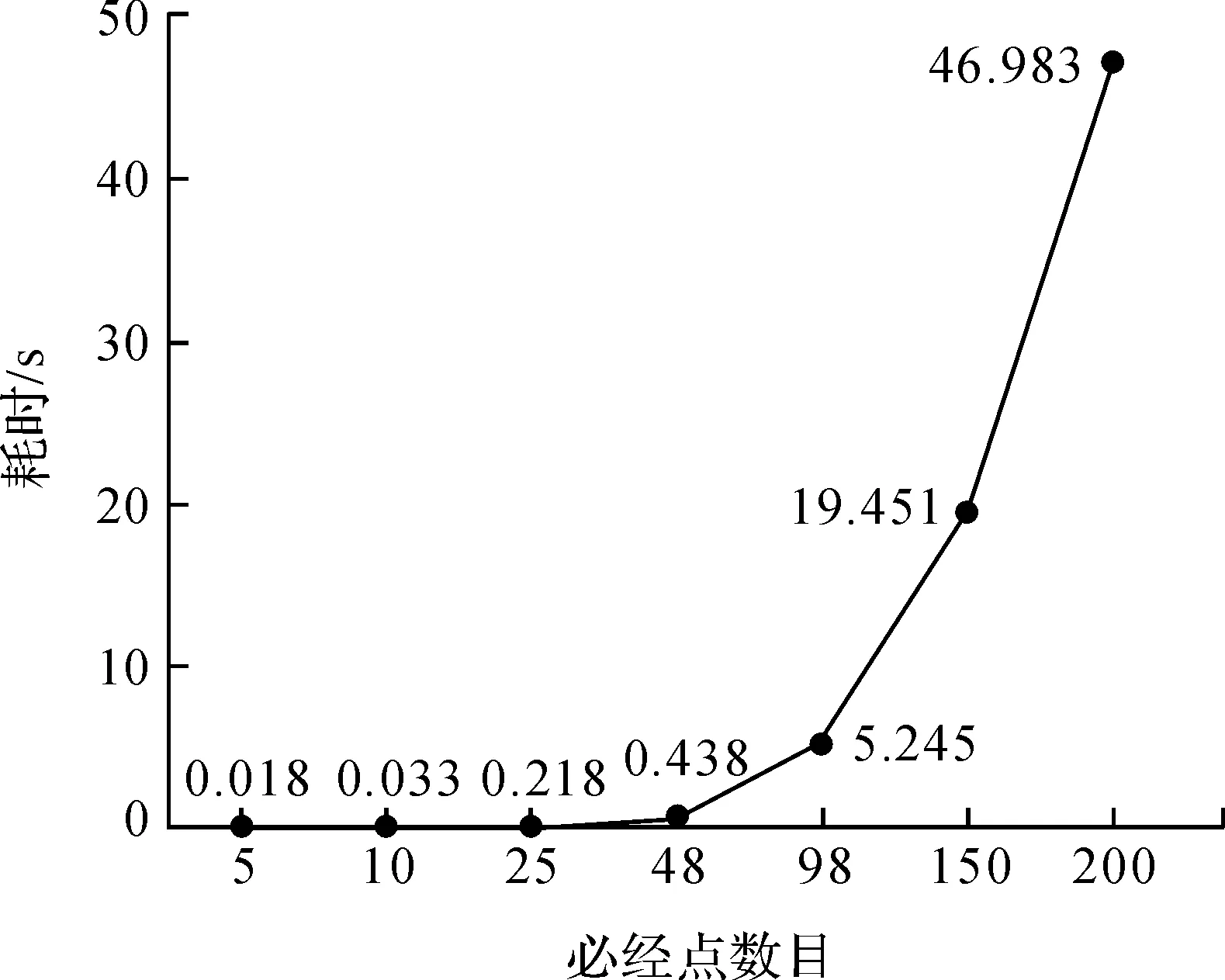
图6 指定网络规模算法时间
表3展示的是当必经点集规模为10时,网络节点规模分别为25,50,100条件下,加入减枝的回溯法和本文算法的平均运行时间与最短路径长度.

表3 2种算法在必经节点集规模为10条件下的实验结果
从表3中可以看出,本文算法和减枝优化的回溯法求解的最短路径权值相近.由于回溯法是确定型算法,可以求解出解空间里的所有解,本文算法的时间消耗相对于减枝优化的回溯法有了量级上的缩减,特别是随着网络规模的增加,回溯法的时间消耗成指数级增长,回溯法只适合求解小规模网络的必经节点集约束型无环最短路问题,所以本文算法的整体性能优于回溯法等确定型算法.
4 结束语
本文基于改进遗传算法和Dijkstra破环策略提出了解决必经点集约束型无环最短路问题的算法,通过加入BNSMS变异策略,提高了遗传算法的收敛速度,扩大了遗传算法的局部搜索能力.对于节点规模大而必经节点集规模小(100以内)的网络有较高的效率,但随着必经节点集的增加,算法的时空效率逐渐减弱,该问题有待进一步研究和探讨.
[1] 张泓,李爱平,刘雪梅.面向TSP求解的混合蚁群算法[J].计算机工程,2009,35(8):34-37.
[2] 蔡光跃,董恩清.遗传算法和蚁群算法在求解TSP问题上的对比分析[J].计算机工程与应用,2007,43(10):96-98.
[3] LIN Z W, FU J Z, SHEN H Y. Tool path generation for multi-axis freeform surface finishing with the LKH TSP solver[J]. Computer-Aided Design, 2015,69:51-61.
[4] LETCHFORD A N, Nasiri S D, Theis D O. Compact formulations of the Steiner Traveling Salesman Problem and related problems[J]. European Journal of Operational Research, 2013,228(1):83-92.
[5] 冯琳耀,袁林旺,罗文,等.节点约束型最短路径的几何代数算法[J].电子学报,2014,42(5):846-851.
[6] 黄书力,胡大裟,蒋玉明.经过指定的中间节点集的最短路径算法[J].计算机工程与应用,2015,51(11):41-46.
[7] IBARAKI T. Algorithms for Obtaining Shortest Paths Visiting Specified Nodes[J]. Siam Review, 1973,15(2):309-317.
[8] 曾文飞,张英杰,颜玲.遗传算法的基本原理及其应用研究[J].软件导刊,2009(9):54-56.
[9] 孙年芳.遗传算法求解TSP问题[J].长春理工大学学报(高教版),2009(2):123-124.
[10] 吴宏超,刘检华,唐承统,等.基于改进A*算法的管路自动布局设计与优化方法[J].计算机集成制造系统,2016,22(4):945-954.
[11] 王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002:10-12.
ResearchontheLoop-freeShortestPathAlgorithmwithNecessaryNodesConstraint
LI Dong, YAN Yi, WANG Dandong, WANG Qiang
(SchoolofComputer,HangzhouDianziUniversity,HangzhouZhejiang, 310018,China)
Based on the genetic algorithm and the Dijkstra algorithm, a method to solve the problem of the loop-free shortest path with necessary nodes constraint is proposed. The problem is decomposed into a special asymmetric ATSP problem and eliminates the loop path problem. Firstly, this paper uses genetic algorithm to solve the problem of special asymmetric ATSP and then obtains the optimal sequence of necessary nodes set. But the path composed of the optimal sequence consists of loop. In order to solve the problem of loop path, a segmented Dijkstra destruction strategy is designed. Finally, it is proved that the algorithm is effective and feasible through the experiments. And compared with the traditional method, the efficiency of time has been greatly improved.
necessary nodes constraint; genetic algorithm; Dijkstra; shortest path; eliminate the loop path
TP301.6
A
1001-9146(2017)05-0044-07
2016-00-00
李东(1989-),男,安徽临泉人,硕士研究生,嵌入式与智能控制.通信作者:严义教授,E-mail:yybjyyj@163.com.
10.13954/j.cnki.hdu.2017.05.009

