G1约束下基于三次内点插值的曲线逼近方法

金佳培，赵伟华，曾 宇，陈小雕

(杭州电子科技大学计算机学院，浙江 杭州 310018)

G1约束下基于三次内点插值的曲线逼近方法

金佳培，赵伟华，曾 宇，陈小雕

(杭州电子科技大学计算机学院，浙江 杭州 310018)

讨论了平面曲线的逼近问题，并提出了基于三次Bézier曲线插值的逼近算法.首先给出了插值三点三切向的三次Bézier曲线的计算公式，其本质上等价于一元三次方程的求解问题，并讨论了相关插值曲线的存在性.该插值曲线具有高达6次的逼近阶，可期望获取更好的逼近效果.然后，已满足误差的部分保持不变，针对不满足误差的部分，事先估算参数区间的划分段数，并计算每一小区间对应的逼近曲线.多段插值Bézier曲线自动具有G1连续性，可进一步合并成C2连续的三次B样条曲线.该方法只需修改不满足误差的局部曲线段，具有修改的局部性.数值实例证明了该方法具有更好的逼近效果和计算效率.

等距；逼近；内点插值法；三次Bézier曲线

0 引 言

等距曲线即平行曲线在计算机辅助设计(CAD)/计算机辅助制造(CAM)等领域有着广泛的应用[1].在实际的CAD/CAM系统中，往往需要使用NURBS曲线来逼近等距曲线，要求满足给定的精度，其关键指标或难点在于尽可能好的逼近效果、尽可能高的效率、自交情况的处理.本文讨论前两种指标，使用合理的计算量，在给定段数限制下获取尽可能高的逼近精度，或在给定精度限制下使用段数尽可能少的曲线，目前主要有3类方法.一是基于控制多边形的方法[2-4]，在给定曲线的控制多边形基础上，为每一个控制点增加一定方向及等距距离的平移，或通过数值迭代的方法加以进一步改善.二是圆逼近方法[5-7]，应用单位圆弧U(s(u))来逼近对应的单位法向曲线N(u)，最终得到的逼近曲线为C(u)+rU(s(u))给出的2个端点及其的导数，计算插值的单位圆弧比较容易的，关键在于参数化函数s(u)的选择，缺点是结果调整方面不够灵活[8].三是插值方法[9-11].标准Hermite插值方法的关键是估算逼近曲线端点处的导矢量.在空间曲线的情况下，文献[9]应用插值给定曲线的内点改进了插值效果.文献[10-11]采用三次Hermite曲线来逼近等距曲线.Josef H.等[10]提出了用最小二乘法来求解逼近问题，但是求解效果不如预期理想.当偏移曲线变得接近平坦时，文献[11]的方法变得很不稳定.端点处具有相同导数和曲率的两条曲线，内部形状也可以有很大的差别.因此，基于端点信息的方法获取的逼近曲线只有一种结果，很多情况下，获取的逼近效果很不稳定，甚至很差.本文以等距曲线为例，讨论基于三次Bézier曲线插值的曲线逼近方法.

1 带G1约束的内点插值法

1.1 三次Bézier曲线的插值问题

P0=Q0，P3=Q1，P1=Q0+αT0，P2=Q1-βT1

(1)

紧接着是如何确定α和β的值.内点插值法及其逼近效果如图1所示.图1(a)中，两条端点重合但不同形状的曲线，在端点处具有相同的导数和曲率；图1(b)中，当要求逼近曲线和原始曲线相切于原始曲线的某个内点时，在Hausdorff距离的度量下，逼近曲线也可以非常地接近原始曲线.基于这个观察，给定一个内点，本文推导出一个非线性方程组，并最后转化为一个单变量三次方程，通过该方程的求解，确定式(1)中α和β的值，从而确定三次Bézier插值曲线的控制点.

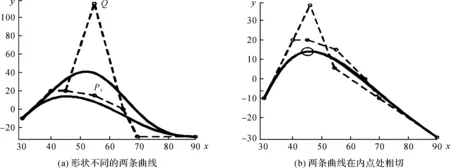
图1 内点插值法及其逼近效果示意图

1.2 公式推导

(2)

式(2)中的前2个方程是关于α和β的线性方程，求解可得

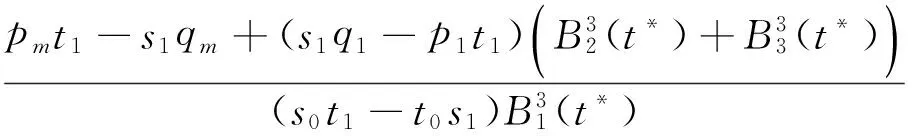
(3)

将式(3)代入式(2)中的第3个方程中，化简后得到一个关于未知数t*的三次方程

H(t*)=h3t*3+h2t*2+h1t*+h0=0.

(4)

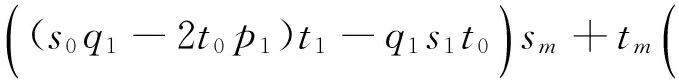
若式(4)中H(t*)在[0，1]内有多个根，则选取最接近(u*-a)/(b-a)的根.将t*的值代入式(3)，得到α和β的值.从而由式(1)得到最终的插值曲线.

1.3 插值曲线的存在性讨论

若Y″(a)X′(a)-Y′(a)X″(a)≠0，

sm=s0+X″(a)(u*-a)+X‴(a)(u*-a)2/2+O(h3)，
s1=s0+X″(a)(b-a)+X‴(a)(b-a)2/2+O(h3)，
tm=t0+Y″(a)(u*-a)+Y‴(a)(u*-a)2/2+O(h3)，
t1=t0+Y″(a)(b-a)+Y‴(a)(b-a)2/2+O(h3)，
pm=p0+X′(a)(u*-a)+X″(a)(u*-a)2/2+O(h3)，
p1=p0+X′(a)(b-a)+X″(a)(b-a)2/2+O(h3)，
qm=q0+Y′(a)(u*-a)+Y″(a)(u*-a)2/2+O(h3)，
q1=q0+Y′(a)(b-a)+Y″(a)(b-a)2/2+O(h3).

(5)

当参数区间的长度h=b-a足够小时，使得上述的泰勒展开式(5)成立，则有如下定理.

定理当参数区间长度h足够小使得式(5)成立时，式(4)中的H(t*)在区间(0，1)内至少有一实根.

证明首先将式(5)分别代入H(0)和H(1)得H(0)=-0.0625(Y″(a)X′(a)-Y′(a)X″(a))2h3+O(h4),H(1)=0.0625(Y″(a)X′(a)-Y′(a)X″(a))2h3+O(h4).当Y″(a)X′(a)-Y′(a)X″(a)≠0时，有H(0)<0且H(1)>0.由中间值定理知，存在t*∈(0，1)使得H(t*)=0.证毕.

1.4 内点参数u*的启发式设置方法

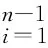
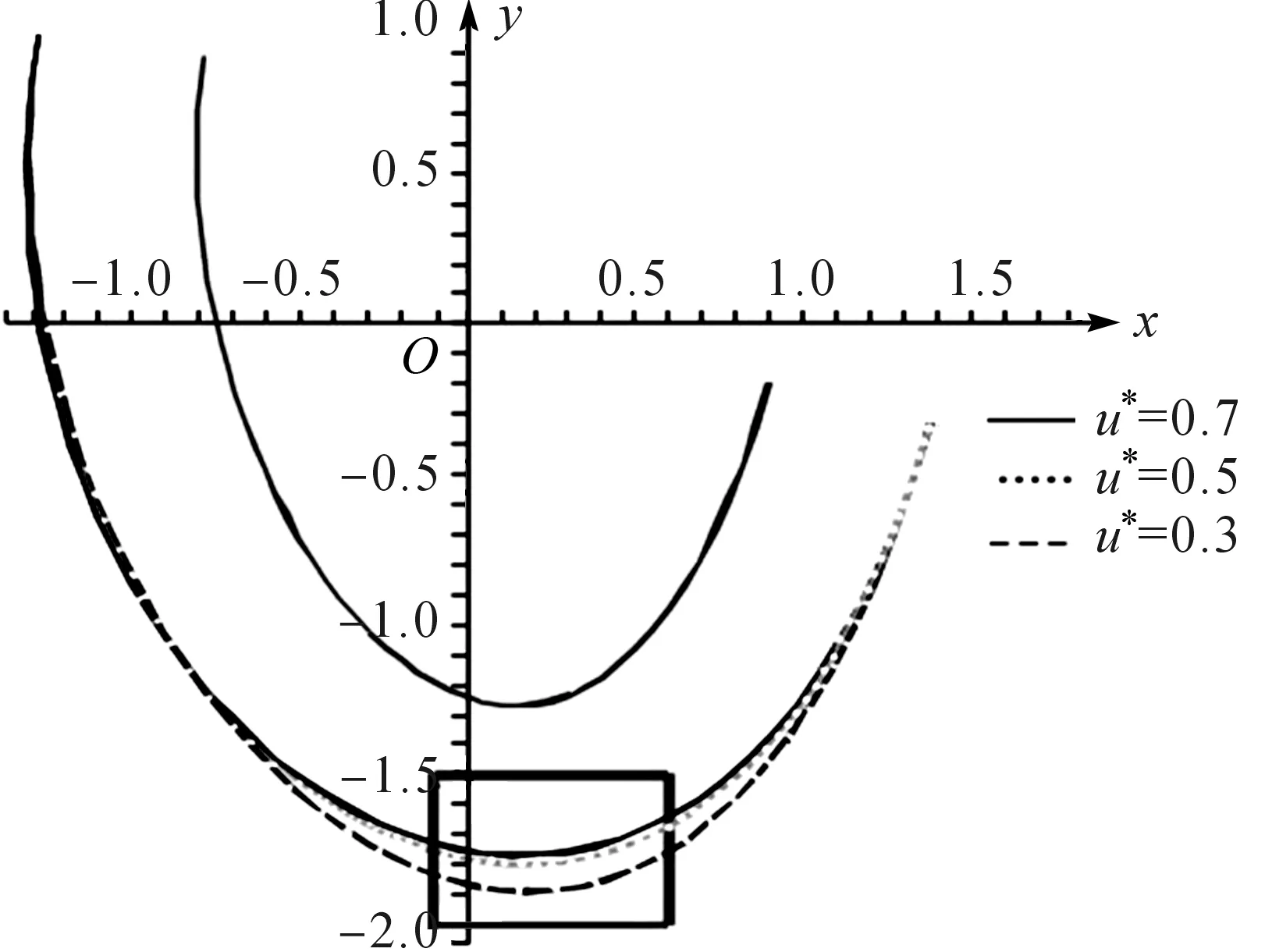
图2 选择不同的u*及其相应的逼近曲线

另外，本文提出了一个启发式的方法来确定u*的值，不同的u*及其相应的逼近曲线如图2所示，给定的曲线是没有拐点的.图2分别绘制了给定曲线，以及对应u*等于0.3，0.5和0.7时的逼近曲线；相应的等距曲线与逼近曲线之间的Hausdorff距离分别为0.120 6，0.031 1和0.021 2，其中u*=0.7对应的曲线具有最佳的逼近效果，而矩形框内的逼近效果不佳.这个例子中，给定曲线的曲率在参数um=0.68时达到最大，非常接近0.70.在本节的启发式方法中，如果给定曲线的曲率是单调的，那么参数u*可以简单设置为(a+b)/2；否则，u*的值可以设置为um，即全局或局部最大曲率发生处对应的参数.然后，根据式(3)可得到α和β的值，以及相应的插值曲线.

1.5 误差的逼近阶分析

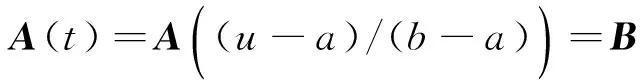
φ(a)=a，φ(u*)=u*，φ(b)=b，φ′(a)=λ1，φ′(u*)=λ2，φ′(b)=λ3.

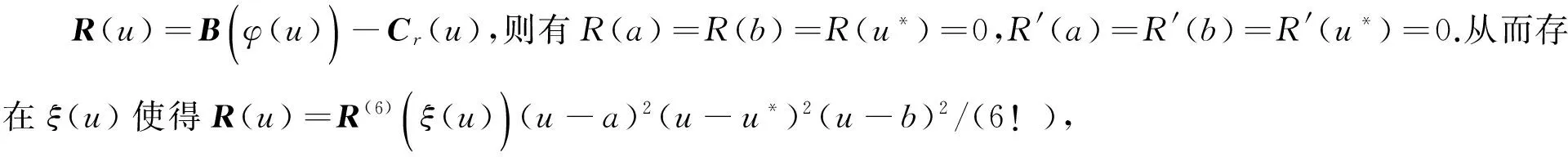
1.6 生成C2-连续逼近B样条曲线

首先是产生G1连续逼近三次Bézier曲线线段.若一条三次Bézier插值曲线已经满足给定的逼近误差，则该曲线已经是C2-连续，直接输出该曲线.否则，依据1.5节的方法估算划分参数子区间，将等距曲线细分为若干个小区间段，对应小区间内已经满足误差的曲线段不必重新计算，未满足误差的小区间局部加细直到满足误差即可.然后采用文献[6]中的方法，将两条G1连续的三次Bézier曲线合并成一条C2-连续的三次B样条曲线.最后，可得到C2-连续的逼近B样条曲线.

2 实例比较与讨论

本节演示一些例子说明内点插值方法，并与已有的方法进行比较.一般来说，文献[2]和文献[3]中基于控制多边形的方法在已有的方法中效率是最快的.插值方法是计算时间与对应逼近效果之间的一个折衷.文献[7]、文献[11]中的插值方法速度快，但相应的逼近效果可能一般，甚至存在算法不稳定的问题.文献[7]中的标准的三次Hermite插值方法通过端点处曲率的插值在不同的参数化方法下，可以产生相同的逼近曲线，但它对曲率比较敏感.通过选择合适的u*值，内点插值方法可以产生一个更好的效果，平均计算时间在几毫秒到几十毫秒之间.

例1图3显示了有4个控制点的凸三次Bézier曲线的实例.图3(a)对应的偏移半径为r=0.5，其中实心曲线来自于新方法，选定内点的参数对应为给定曲线最大曲率发生处的参数，对应由新方法产生的逼近曲线是一个三次Bézier曲线，与等距曲线几乎是一致的.其它不同线型虚线表示的曲线分别是由文献[2]方法、文献[3]方法、文献[4]方法、文献[10]方法和文献[11]方法所得到的.图3(b)表示等距半径为0.2，0.4，0.6，0.8，1.0，1.2时对应的逼近曲线.

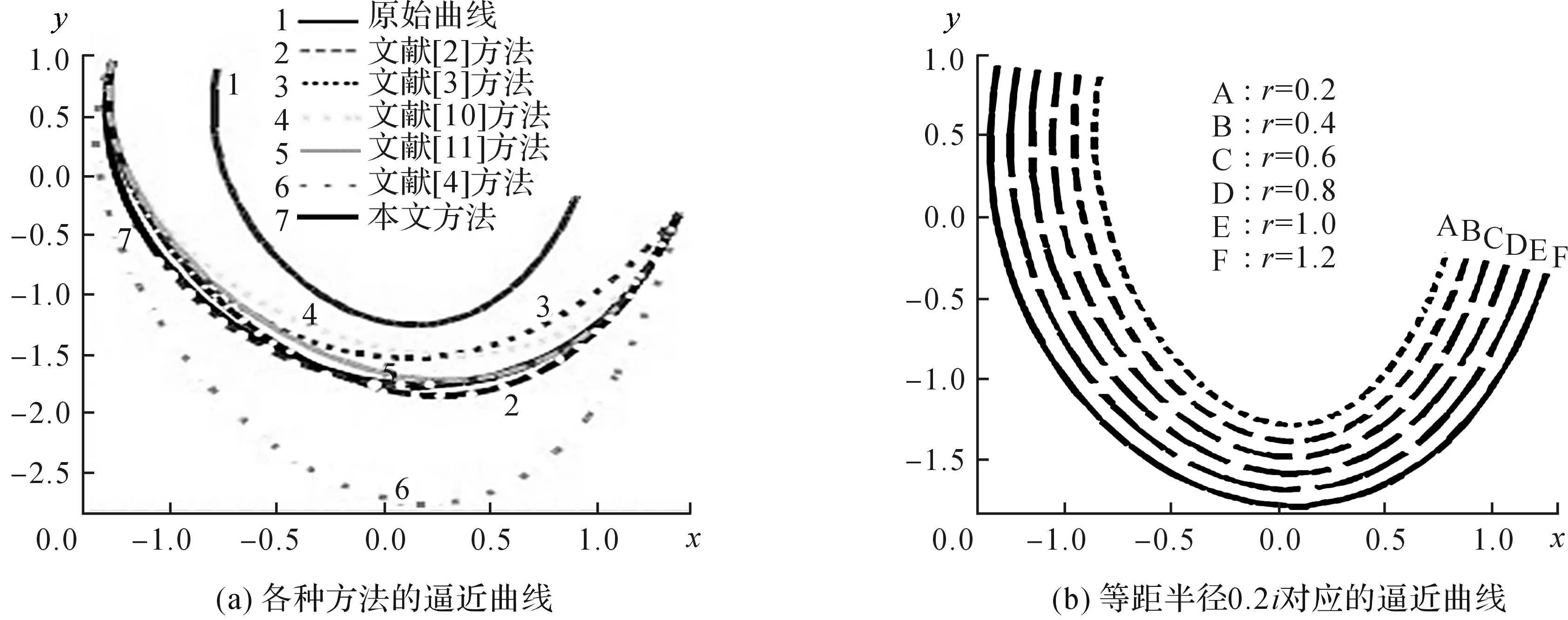
图3 一个凸三次Bézier曲线实例

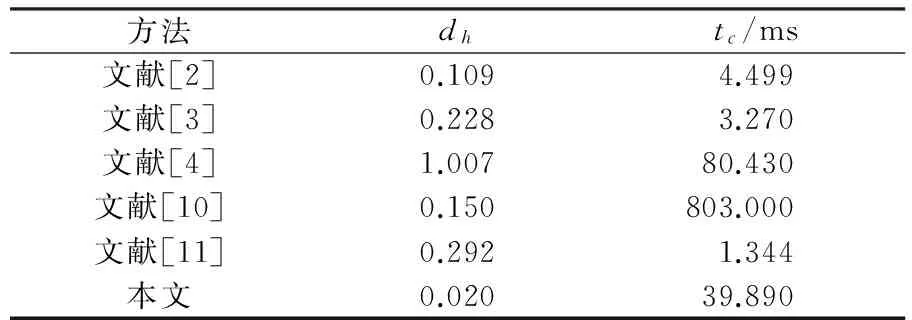
方法dhtc/ms文献[2]0.1094.499文献[3]0.2283.270文献[4]1.00780.430文献[10]0.150803.000文献[11]0.2921.344本文0.02039.890

相应的等距曲线与逼近曲线间的Hausdorff距离以及平均计算时间如表1所示.本例中，新方法的逼近效果是最好的，文献[2]方法次之.文献[10]的最小二乘法所需的计算时间是所有列出的方法中最多的，文献[3]方法和本文方法的计算时间次之，文献[2]、文献[4]和文献[11]方法的计算时间相对更少.

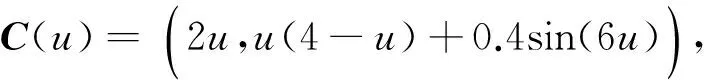
图4 非多项式曲线实例

例3图5显示了更多的例子，将文献[7]、文献[11]中的标准三次Hermite插值方法和本文方法作比较.从图中可以明显看出本文方法得到的曲线具有最小的逼近误差.本例表明，与标准的三次Hermite插值方法相比，本文方法可以提高相应的逼近效果.

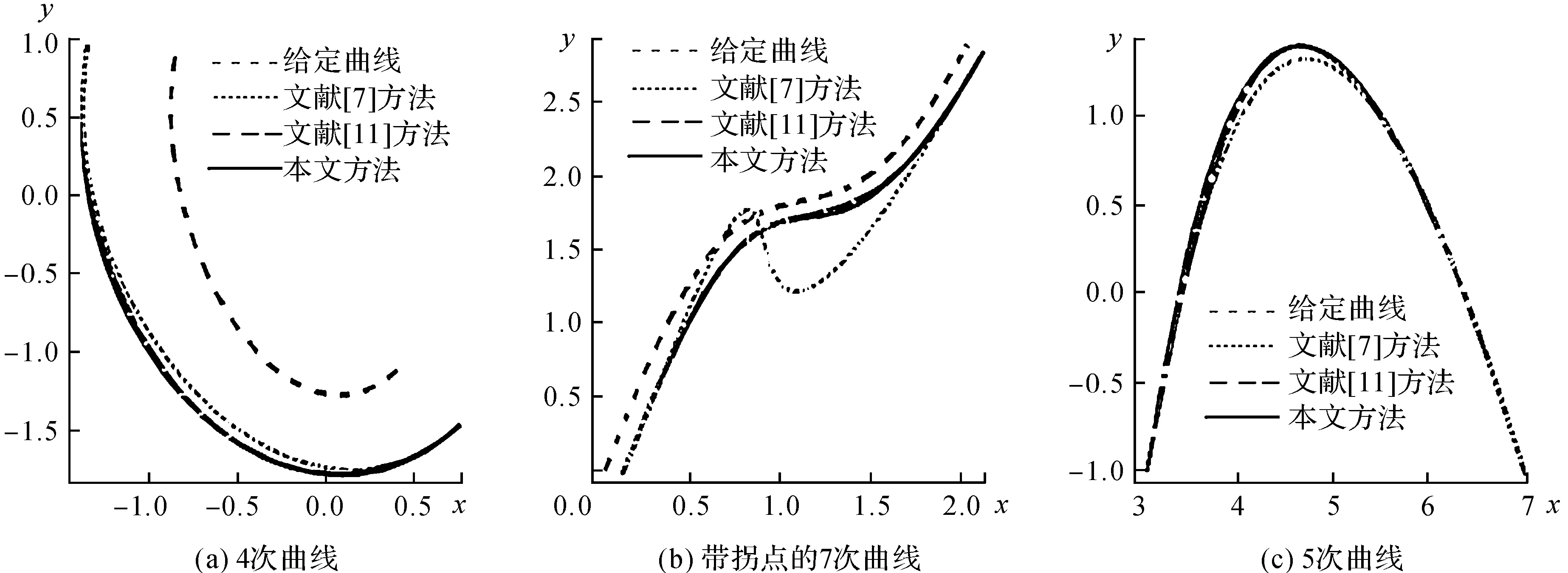
图5 文献[7]、文献[11]中Hermite插值方法和本文方法的比较

3 结束语

本文提出的内点插值方法本身计算相对简单，且具有计算的局部修改性，即当曲线局部编辑后，仅仅需要局部修改区域的计算.与全局计算方法相比，具有很高的计算效率，可以方便曲线的编辑.本文方法不需要控制多边形的信息，可应用于包括非多项式或任意形式表示的光滑曲线.本文方法理论上可达6次逼近阶，实例也表明了它有更好的逼近效果.未来工作仍有很大的发展空间.首先，当给定曲线形状比较复杂时，如何预先进行分段，使得每一小段曲线，本文的内点插值法得到的曲线可以满足给定的误差.其次，内点参数u*的最优化问题仍然未解决.再次，等距曲线本身的自交处理，即裁剪掉自相交的部分，也是未来可能的研究方向.最后，能否略过Bézier曲线局部逼近的步骤，直接使用B样条曲线来表示最终的逼近曲线，也是个值得讨论的问题.

[1] HU Q. Constrained polynomial approximation of quadric surfaces[J]. Applied Mathematics & Computation, 2014,248(248):354-362.

[2] TILLER W, HANSON E. Offsets of Two-Dimensional Profiles[J]. Computer Graphics & Applications IEEE, 1984,4(9):36-46.

[3] COBB E S. Design of sculptured surfaces using the B-spline representation[M]. Salt Lake City: University of Utah, 1984:33-52.

[4] COQUILLART S. Computing offsets of B-spline curves[J]. Computer-Aided Design, 1987,19(6):305-309.

[5] KHAN M, CHEN Z. Approximation of planar offset curves with globally bounded error for B- spline NC tool paths[J]. International Journal of Production Research, 2012,50(23):1-15.

[6] KIM Y J, LEE J, KIM M S, et al. Efficient offset trimming for planar rational curves using biarc trees[J]. Computer Aided Geometric Design, 2012,29(7):555-564.

[7] FAROUKI R T, NEFF C A. Analytic properties of plane offset curves[J]. Computer Aided Geometric Design, 1990,7(7):83-99.

[8] BASTL B, JÜTTLER B, KOSINKA J, et al. Volumes with piecewise quadratic medial surface transforms: Computation of boundaries and trimmed offsets[J]. Computer-Aided Design, 2010,42(6):571-579.

[9] HÖLLIG K, KOCH J. Geometric Hermite interpolation[J]. Computer Aided Geometric Design, 1995,12(6):567-580.

[10] HOSCHEK J, WISSEL N. Optimal approximate conversion of spline curves and spline approximation of offset curves[J]. Computer-Aided Design, 1988,20(8):475-483.

[11] KLASS R. An offset spline approximation for plane cubic splines[J]. Computer-Aided Design, 1983,15(5):297-299.

[12] ZHAO H Y, WANG G J, MATHEMATICS D O, et al. Offset approximation based on reparameterizing the path of a moving point along the base circle[J].高校应用数学学报B辑(英文版),2009,24(4):431-442.

CubicInnerPointInterpolationBasedMethodforApproximatingOffsetCurvesunderG1Constraint

JIN Jiapei, ZHAO Weihua, ZENG Yu, CHEN Xiaodiao

(SchoolofComputer,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Offset curves have wide applications in computer-aided design(CAD) and robot path planning(RPP). Interpolation method needs no information of the control polygon and seems to be more flexible. This paper discusses approximating offset curves and proposes a method based on cubic Bézier inner point interpolation. It derives the formulae of cubic Bézier curves which interpolate three points and three of their directional tangent vectors, which is turned into a univariate cubic polynomial equation; it also discusses the existence of the interpolation curve. It can achieve approximation order of 6, which means to possibly obtain better approximation effect. The cubic interpolation Bézier curves areG1continuous, which can be merged into aC2continuous B-spline curve. The proposed method is a local one, which means that only the segments not satisfying the given tolerance need to be subdivided into several sub-segments, and the number of the sub-segments can be pre-estimated. Numerical examples show that the proposed method can achieve much better approximation effect than previous methods.

offset; approximation; inner point interpolation method; cubic Bézier curve

TP391.41

A

1001-9146(2017)05-0038-06

10.13954/j.cnki.hdu.2017.05.008

2016-11-16

国家自然科学基金资助项目(61672009)

金佳培(1991-)，女，浙江海宁人，硕士研究生，计算机图形图像.通信作者：陈小雕教授，E-mail:xiaodiao@hdu.edu.cn.