基于地形因子改进融雪径流的模拟及验证

穆艾塔尔·赛地，丁建丽※，崔春亮



基于地形因子改进融雪径流的模拟及验证

穆艾塔尔·赛地1,2，丁建丽1,2※，崔春亮3

（1. 新疆大学资源与环境科学学院，乌鲁木齐 830046；2. 绿洲生态教育部重点实验室，乌鲁木齐830046； 3. 新疆水利水电科学研究院，乌鲁木齐 830049）

该文基于传统的气温指标经验融雪径流模型，提出结合高程、坡向和坡度的流域分带及度日因子改进计算方法，定量描述流域地形特征对气温空间差异与融雪量产生的影响，由此建立基于地形因子改进的融雪径流（snowmelt runoff model，SRM）模型。通过乌鲁木齐河上游山区流域2005-2007年春夏季融雪日径流的模拟和验证，对比分析这传统模型和改进融雪径流模型在数据稀缺流域中的应用效果。结果表明，2种模型模拟2005-2007年春夏季融雪日径流均有较好的模拟效果。比较传统模型，基于地形因子改进的融雪径流模型具有更高的模拟精度，通过流域分带和度日因子数计算的改进，减少了模拟误差，3 a平均的拟合优度2值从0.77增加到0.80，均方根误差从5.7减少到5.35 m3/s，模拟精度有所提高。可见，建立的基于坡向和坡度等地形因子改进的融雪径流模型在数据稀缺干旱流域融雪径流模拟中具有更好的适用性。

地形；坡度；径流；坡向；融雪；分带；度日因子数

0 引 言

在中国西北干旱、半干旱地区，高山冰雪融水与降水作为绿洲地带的宝贵水源及河川径流的主要补给源，具有重要战略地位。以新疆内陆河流为代表，天山北坡山区流域融雪与降水径流占年径流量的80%以上，冰雪融水补给的比例占36%，对当地人们的生活、生产与环境有直接影响[1-3]。近几十年，全球气候变化对干旱区水文水资源的影响十分显著，气温对山区冰雪覆盖的影响最为明显，造成融雪径流量和径流时间发生变化，春夏季如遇升温天气，极易导致融雪性洪水，对人民生命财产及生产造成较大的损失[4-6]。因此，以融雪径流为主的干旱流域模拟估算径流量及径流时间具有必要性，有利于做好当地水资源规划与开发利用工作。

新疆内陆河山区流域自然地理环境独特，气候条件多样，地形复杂，地面观测站点稀少，资料缺乏，不利于流域融雪过程的精细描述。国内外学者们构建多种水文物质平衡模型，尝试实现数据稀缺流域融雪径流的精确模拟。常用的水文物质平衡模型可分为2种：一种是基于气温指标的经验模型（temperature-index model）；另一种是基于表面物理过程的能量平衡模型（energy- balance model）。气温指标经验模型主要利用度日因子方法，把复杂的地表物理能量平衡过程转换成表面消融与气温之间的线性关系模型[7-9]。对建模方法而言，这2种模型均以融雪量的计算为核心，基于传统度日因子法，加入太阳辐射、积雪反照率和地形因子等其他参数和变量改进模型并提高精度[9-13]。由于气温资料容易获取，气温指标经验模型在融雪径流模拟计算中得到了广泛的应用。在数据稀缺流域，气温指标经验模型的应用具有一定的挑战性，主要是因为在资料稀缺条件下模型参数的适当选取和模型适用性的限制。

作为一种气温指标经验模型，融雪径流（snowmelt runoff model，SRM）模型可用于模拟和预报山区流域季节性、全年和序列多年的融雪日径流过程。SRM模型于20世纪80年代首次推出后，在世界的众多流域中得到应用和试验，结果已通过世界气象组织的评价与测试，成为结合应用遥感技术与水文分析来研究流域融雪径流的常用模型[1]。目前国内学者把SRM模型成功应用到西北干旱区融雪型补给河流的径流模拟中。如：马虹等[4,14-16]在数据稀缺条件下应用SRM模型，结合气候变化情景模拟，获得了干旱半干旱流域水文过程模拟较理想的研究成果。

SRM模型主要利用流域高程分带和度日因子法，把大于临界气温的度日因子数转算成融雪深度，通过叠加各高程分带的融雪径流来确定流域径流量，为数据稀缺流域提供了比较理想的日径流模拟预报方法[1-2]。该方法的缺点是度日因子数的计算仅考虑气温随海拔高程变化特征，对由地形遮蔽、坡度、坡向等地形特征引起的空间差异性不能做出合理的解释[17-18]。高海拔山区不同的坡向和坡度上地面接受的太阳辐射量存在一定的差异，因而气温变化也有差异，由此进一步影响积雪的分布、再分布和消融过程[18-19]。通过一定的方法在资料缺乏的山区流域定量描述坡向和坡度等地形因子对气温的影响，并由此改进度日因子及融雪量的估算具有独特研究价值。

本文选择乌鲁木齐河上游山区小流域，在数据稀缺条件下引入坡向和坡度等地形因子，提出结合海拔高程、坡向和坡度的流域分带及度日因子计算方法，改进传统SRM模型，建立基于地形因子改进的SRM模型，对比传统和改进后的SRM模型的模拟能力，验证基于地形因子改进的SRM模型在数据稀缺流域融雪径流模拟中的适用性，以期为干旱区缺少资料流域的水文模拟提供理论依据。

1 基于坡向和坡度的SRM模型改进

1.1 传统SRM模型

SRM模型计算融雪日径流利用描述流域特征的一些变量和参数，分别计算每天的融雪和降水对径流的贡献，并将其叠加到退水流量上，得到流域每天的融雪日径流量，计算公式如下：

式中为径流日序列；Q1为第+1天的日平均流量，m3/s。Q1由前1天融雪产生的水量、降雨产生的水量和退水流量组成：融雪产生的水量是日融雪量（cm/d）、积雪覆盖率、融雪径流系数c和流域面积（km2）的乘积；降雨产生的水量是日降水量（cm）、降雨径流系数c和流域面积（km2）的乘积；退水量是第天的日平均流量Q（m3/s）和退水系数的乘积。积雪覆盖率为积雪面积与流域面积的比值；为退水系数，表示没有融雪和降水的时间段内径流的下降值，k=Q+1/Q（1为退水期的日序列）[2]；10 000/86 400为由径流深到径流量的转换系数[2,20]。

传统SRM模型计算融雪径流利用度日模型。度日模型利用高程分带的平均海拔与气温直减率推算流域不同高程上的度日因子数，对相同海拔处不同坡向和坡度的气温差异不给予解释，其计算式为

1.2 基于地形因子改进的SRM模型

基于地形因子改进的SRM模型在传统SRM模型的高程分带方法中增加坡度和坡向因子，提出结合高程、坡向和坡度的流域分带及度日子因子计算方法，其融雪量的计算式为

式中ΔT和ΔT是基于坡向和坡度的气温调整值，℃；[(T–0+ΔT)+ΔT·ΔT]代表改进后的度日因子数，℃。

坡向和坡度通过太阳辐射的空间分布来影响气温。东南西北不同坡向上太阳辐射达到地面的时间存在差异，坡面和水平面上分布的太阳辐射量大小亦不等。Kang等[21-22]研究山区坡度和坡向与融雪量之间的关系，定量描述气温随坡向变化的空间特征，表1显示气温随坡向变化调整值。

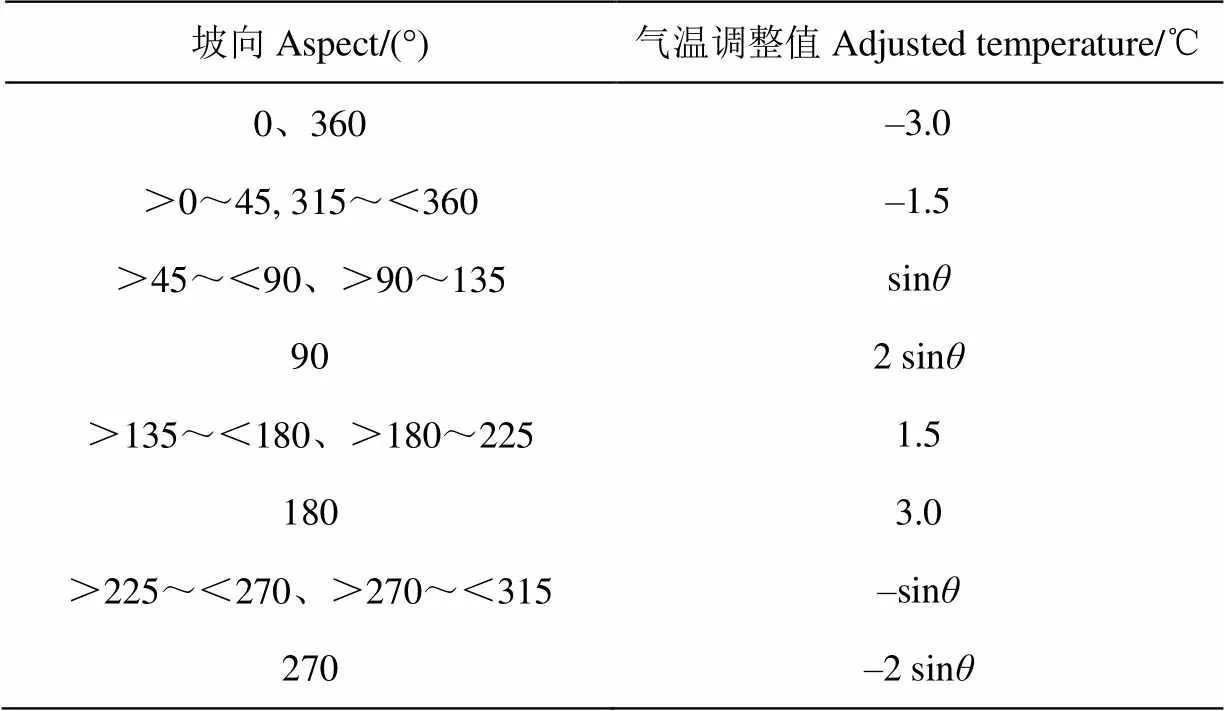
表1 气温随坡向变化调整值

注：气温调整参数。

Note:is adjusted temperature parameter.

1 d之内不同时间段山区地面接收的太阳辐射随时间逐步减少，气温也随之下降。表1中通过引入参数来定量表达1 d之内气温随时间的变化特征[21]。

=·/12 （5）

式中为模拟时间步长，取值范围1～24 h；为常数，取值为180°。结合式（5）和表1可计算基于坡向的气温调整值ΔT。

山区平坦的地面接受太阳辐射比斜坡多，气温也随之发生变化，以每隔15°坡度计算气温随坡度变化调整值[21]。计算式如下：

ΔT=0/15 （6）

式中0是坡度，（°）。

T=(TT0+ΔT)+ ΔT·ΔT（7）

2 模型应用及评价

2.1 研究区概况及数据来源

乌鲁木齐河水系（图1）位于天山北坡中段，处于86°45′E～87°56′E，43°00′N～44°07′N之间，发源于天山北坡的喀拉乌成山主峰—天格尔Ⅱ峰，流向东北，出山口后至乌拉泊折为正北，穿过乌鲁木齐市区，至米泉市西北部的古尔班通古特沙漠消失，全长为214.3 km，集水面积为924 km2，是一条冰雪融水补给为主的混合型河流，径流组成中融雪和降雨补给分别占36%和37%，在英雄桥水文站山口后进入山前平原，经过大西沟水管站被全部引入渠道和水库。据英雄桥水文站数据统计，1958—2012年，平均年径流量2.41×108m3，年平均气温是1.7 ℃，年降水量454.5 mm。本文选择出山口以上山区流域作为融雪径流模拟区，面积为1 073.64 km2，河长为62 km，海拔高程为1 683～4 459 m，平均海拔为3 066 m[2-3]。

图1 研究流域位置及水文气象站点分布

本文所利用的数据由分布在流域境内的3个观测站点提供。其中有2个水文站和1个气象站，分别为出山口的英雄桥水文站、海拔高程1 920 m；上游中部的跃进桥水文站、海拔高程2 313 m；在源流区的大西沟气象站，海拔高程3 539 m，研究流域观测站点的分布如图1所示。收集到的实测资料与遥感数据包括：1）英雄桥和跃进桥水文站2005—2007年的实测日平均流量、日平均气温、日降水量数据。大西沟气象站同期的实测日平均气温和日降水量数据；2）英雄桥和跃进桥水文站多年序列的月平均流量和年径流量、气温和降水量数据；3）积雪覆盖信息用中分辨率成像光谱仪（MODIS）陆地卫星（Terra）产品代号为MOD 10A2的积雪覆盖8 d最大化合成500 m积雪覆盖资料。选择乌鲁木齐河流域2005—2007年3—8月每年24景，共72景MOD 10A2数据提取流域积雪覆盖面积。

SRM模型以高程分带的方式进行流域空间离散，以日为时间步长对融雪期、全年和序列多年的径流量模拟进行时间离散化。空间离散化的目的是区分地形、气候等流域特征因子的垂直分布规律，形成一定数量的高程分带[20]。利用DEM数据把乌鲁木齐河流域划成分5个高程分带，用A、B、C、D和E记。分带A的高程为1 683～2 183 m，面积为88.77 km2；分带B的高程为＞2 183～2 683 m，面积为276.88 km2；分带C的高程为＞2 683～3 183 m，面积为263.27 km2；分带D的高程为＞3 183～3 683 m，面积为284.66 km2；分带E的高程为＞3 683～4 459 m，面积为160.06 km2。融雪径流以日为步长模拟2005—2007年春夏2季流域日径流。

2.2 模型参数值获取

2.2.1 气温

利用3个观测站的日平均气温和海拔高程计算流域气温直减率以及5个高程分带平均海拔上的度日因子数。其中，分带A和B利用英雄桥与跃进桥水文站之间的温度直减率以及日平均气温，通过式（3）计算基于海拔的气温调整值。对高程分带C、D和E以及12个子分带首先用跃进桥和大西沟之间的气温直减率以及各站的日平均气温，通过式（3）计算基于高程的度日因子调整值；其次结合表1和式（5）计算基于坡向的气温调整值；再次用式（6）计算基于坡度的气温调整值；最后按照式（7）计算每个分带的度日因子。3个观测站之间的气温直减率和基于坡向和坡度的温度调整值结果如表2和表3所示。利用DEM数据计算研究流域的坡向分布，并根据表1计算各坡向分组对应的流域面积，结果表明正东坡（90°）、正南坡（180°）、正西坡（270°）和正北坡（0°或360°）所对应的流域面积很小，其累计面积仅占流域总域面的0.87%，故计算气温随坡向的调整值时给予忽略。基于坡向的气温调整值计算主要考虑其他4个坡向分组，对应地把积雪集中分布的高海拔分带C，D和E各分成4个子分带，分别用C1、C2、C3、C4，D1、D2、D3、D4以及E1、E2、E3、E4记，形成A、B和12个子分带共14个融雪量计算单元。

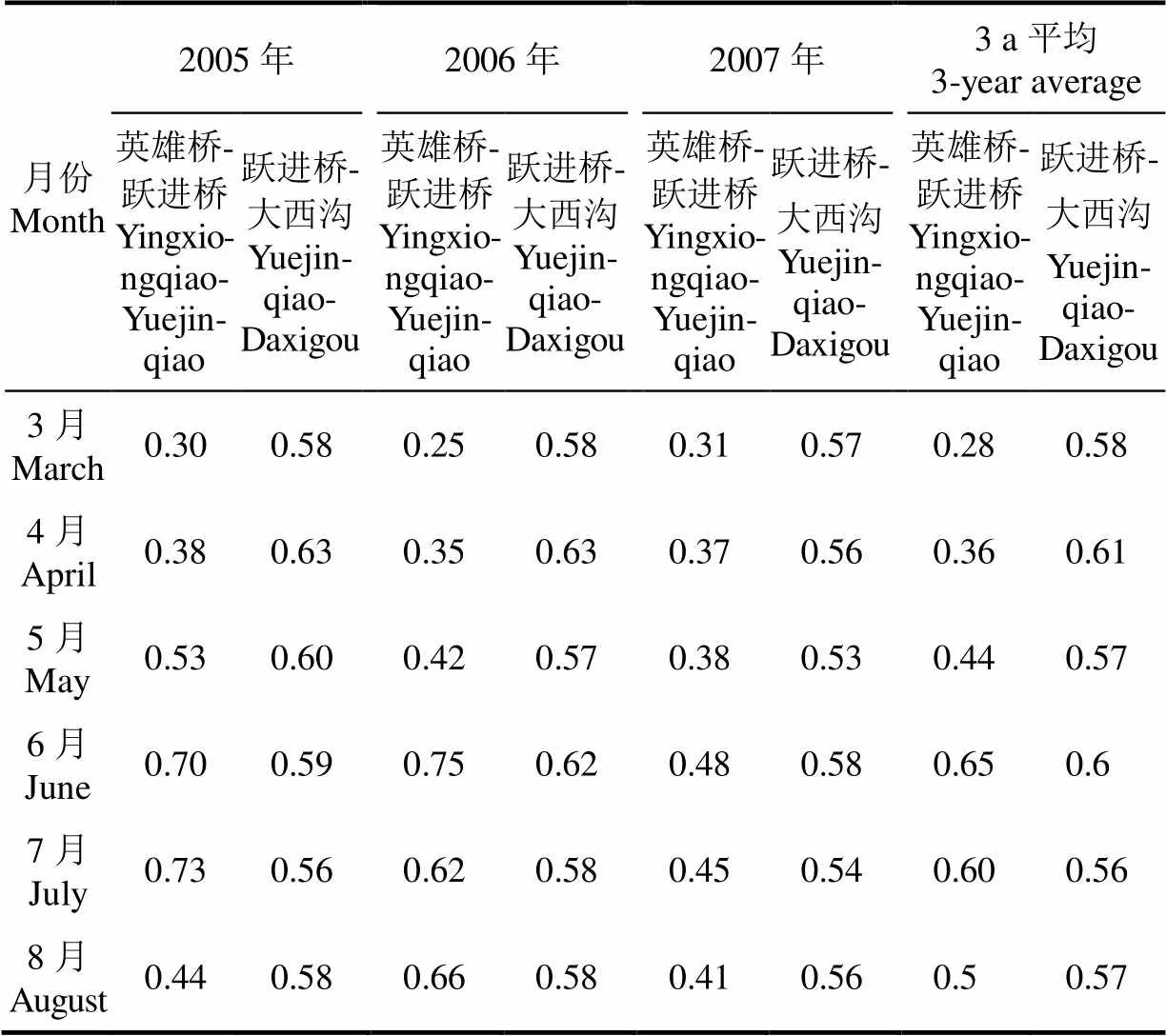
表2 乌鲁木齐河流域2005—2007年气温直减率

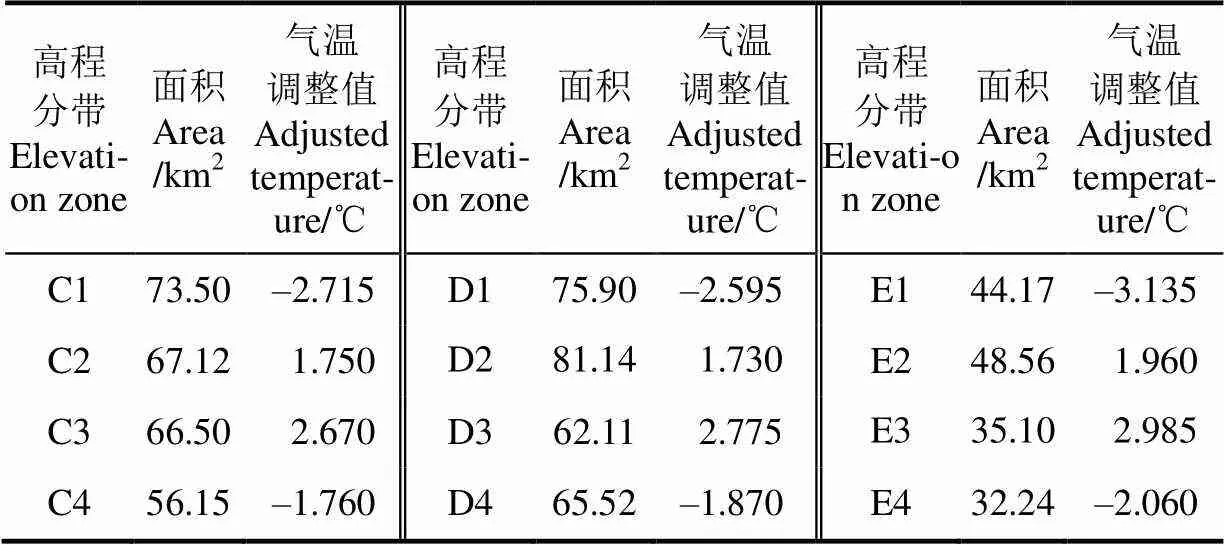
表3 基于坡向和坡度的高程分带面积及其气温调整值

2.2.2 降 水

水文模型的运行结果在很大程度上取决于输入数据的数量和质量[23]。山区流域降水观测数据稀缺而具有很大的不确定性，局部降雨特征显著，正确估算流域分带的降水量十分困难。通常利用观测数据和一定的降水梯度推算流域分带平均高程上的日降水量[24-26]。乌鲁木齐河流域3个观测站的降水资料分析结果表明，3个观测站的降水量数据没有显著的相关性或统一的变化趋势，无法利用实测资料确定流域降水梯度。因此，通过流域径流量和降水量的相关性来选择3个观测站中对流域代表性较好的降水量数据，并由此确定流域降水量的插值推算方案。对径流量和降水量而言，大西沟站的降水量与流域径流量之间存在相对较好的相关性，3 a均相关系数达0.52（<0.05）；跃进桥和英雄桥站的降水量与流域径流量之间的相关性不显著，3 a平均相关系数分别为0.23和0.20（>0.05）。大西沟气象站位于研究流域上游边缘高海拔山区，其观测数据不能充分反映流域7—8月洪水期中山地带和出山口发生的局部降雨，需要进一步利用英雄桥和跃进桥站的降水量把低海拔山区的降水量加入到模型计算中。因此，本文通过多次模拟和调整，最终确定产生最好模拟效果的降水输入方案，在3—6月平水期利用大西沟气象站的降水量，采用SRM模型最常用的3%的降水梯度[20]将大西沟气象站海拔3 539 m的降水量数据插值推算到流域分带的平均高程上；7—8月洪水期结合利用3个观测站的降水量数据，在高程分带A上利用英雄桥水文站的降水量，在高程分带B和C上利用跃进桥水文站的降水量，在高程分带D和E上利用大西沟气象站的降水量，并按照3%的降水梯度计算每个分带平均高程上的日降水量。

2.2.3 积雪覆盖率

与常用的NOAA-AVHRR数据相比，MODIS数据地理定位精度高，而且不需要在地表覆盖物之间进行分类，积雪信息可以直接读取[27-30]。MOD 10A2数据对积雪覆盖具有最大化、对云覆盖具有最小化的效果。因而，本研究利用MODIS数据提取积雪覆盖信息。2005—2007年3—8月乌鲁木齐河流域MOD 10A2数据受云覆盖影响很小，每年24景MOD 10A2数据云覆盖率分别为0.30%、0.94%和0.20%，可以精确地提取积雪覆盖面积。因此，本文计算积雪覆盖率首先针对消融期的MOD 10A2数据进行筛选，剔除个别受到云覆盖以及新降雪影响的异常数据，再利用线性插值方法获得流域分带积雪覆盖面积序列日资料。图2为乌鲁木齐河流域2005—2007年3—8月3 a平均积雪覆盖率变化曲线。

图2显示，乌鲁木齐河流域积雪从3月开始融化。海拔较低的高程分带A和B上积雪覆盖率较小，融化快，覆盖率迅速下降，到5月底积雪全化完；海拔较高的分带C、D和E上积雪覆盖率高，消融较缓慢。其中，高程分带C上积雪覆覆盖率在6月上旬、高程分带D上在7月中旬达到最小值。高程分带E上消融期为从3月到6月下旬，从7月开始随流域气温下降，积雪消融变慢、覆盖率保持基本稳定，取值为20%左右。

2.2.4 退水系数

根据退水系数公式[2]，可推理出

k+1=x·Q（8）

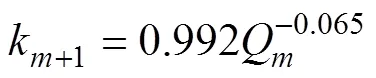
2.2.5 径流系数及度日因子

径流系数表示融雪和降雨对径流的贡献率。SRM模型作为确定性模型，根据流域特征确定径流系数，然后通过流域实测径流及其模拟结果之间的拟合程度优化调整，确定最佳模型[20]。干旱流域融雪与降雨产生的水量在产流过程中通过下渗和蒸散发等发生的耗散比较强烈，径流系数相对较小，但随着海拔升高径流系数呈增大势[20]。因此，乌鲁木齐河流域融雪和降雨径流系数的率定首先根据流域自然地理因素在融雪期内的变化特征进行初步估算，再结合模拟结果和实测结果的拟合程度进行适当的优化调整[1,4,16,20]。流域度日因子的估算主要针对积雪。胡汝骥[24]提出天山山地新雪、细雪、融冻雪等6种雪的密度未超过0.3 g/cm3，随海拔升高积雪深度和密度逐步增大。本文结合杨大庆等[33]在乌鲁木齐河上游的雪密度观测资料与新疆天山雪密度分布相关研究成果[24,31-32]，利用度日因子经验公式[20]计算流域积雪度日因子。5个高程分带的参数估算结果如表4所示。子分带C1～C4、D1～D4以及E1～E4的参数分别与分带C、D和E的参数取值一致。

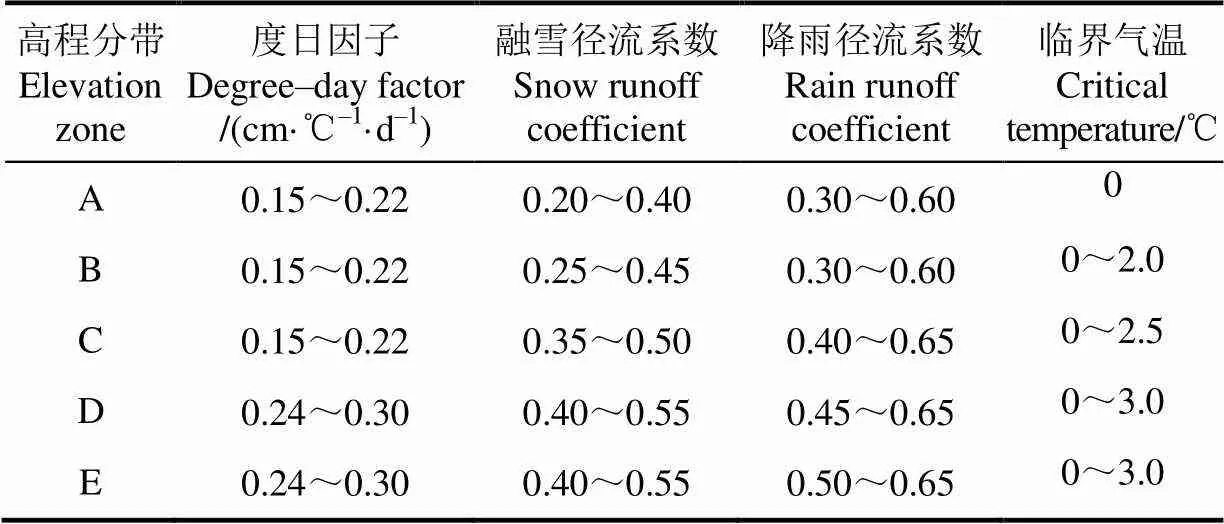
表4 乌鲁木齐河流域融雪径流模拟参数

2.3 结果验证

采用决定系数2，均方根误差（root mean square error，RMSE）和径流总量相对误差（relative error，RE）3个指标判断融雪径流模拟结果。2取值0～1，越接近于1表明模拟精度越高；RMSE取值越小代表模拟值和预测值越接近；RE取值越小代表模拟效果越好。

3 结果与分析

以2007年3—8月为模拟校准期、2005年和2006年3—8月为模拟验证期建立乌鲁木齐河流域融雪径流模型，模型精度如表5所示。可知，基于地形因子改进的高程分带和度日因子改进算法可以优化SRM模型的模拟效果。2007年融雪径流模拟中SRM模型改进后的2，RE和RMSE取值分别为0.84、2.16%和5.80 m3/s，相对传统SRM模型的0.82、4.17%和6.19 m3/s有所改进，减小了模拟误差。对模型验证而言，除了2006年RE值增加之外，改进后SRM模型的模拟效果比改进前传统的SRM模型好。2006年和2005年，改进后2分别达0.78和0.77，较改进前的2值0.76和0.74有所提高；同时，改进后的RMSE值较传统SRM模型有所减少，分别从6.51和4.30 m3/s减少到6.25和4.00 m3/s，提高了模拟精度。可知，改进前后的2种融雪径流SRM模型均有效，而且基于地形因子改进的SRM模型具有更好的模拟结果。2006年径流模拟相对误差增大可能的原因是改进后的模型把流域分成14个分带，使得积雪覆盖率分得更细，与改进前的相比其分布较分散。由此，插值计算后14个分带积雪覆盖总面积较改进前的积雪覆盖总面积减少6%，增大了相对误差。然而，总体而言，改进前模型的3 a平均2值、相对误差（其绝对值）和RMSE值为0.77、5.80%和5.70 m3/s；改进后2值、相对误差（其绝对值）和RMSE值分别达到0.80、5.10%和5.35 m3/s。可见改进后的SRM模型在乌鲁木齐河流域融雪径流模拟获得了比较理想的结果。

图3显示传统和改进后的SRM模型在鲁木齐河上游山区融雪径流的时间序列模拟结果。可知，2种模型模拟值和实测值拟合程度较好，变化趋势一致，对退水过程也有着较好的对应效果。但对峰谷对应出现偏大与偏小，洪峰流量模拟存在较大差异。这是因为山区流域经常发生局部大雨或暴雨等产生洪水径流，地面观测站无法及时监测记录这些突发降水，由此导致洪峰流量的精确模拟比较困难。

表5 传统SRM模型与基于地形因子改进的 SRM模型径流模拟结果评价

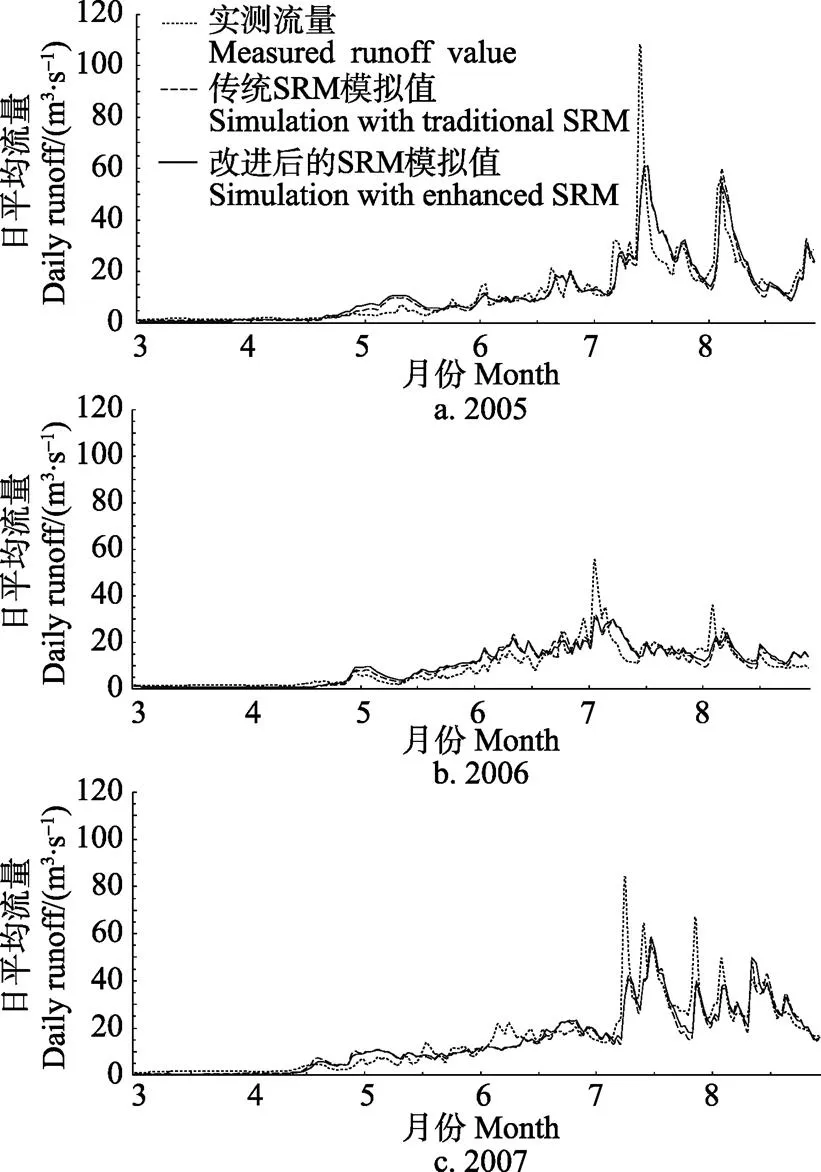
图3 乌鲁木齐河流域春夏季融雪径流模拟

4 讨 论

传统SRM和基于地形因子改进的SRM模型均属于基于度日因子的气温指数经验模型，利用流域高程分带的度日因子和临界气温值，把大于临界气温的度日因子数转算成融雪深度，模型建立成功与否关键在于准确把握气温变量。传统SRM模型对于相同海拔不同坡向和坡度的气温差异不给予解释，度日因子数计算比较简单，利用气温直减率和海拔高程获得。基于地形因子的SRM改进模型以流域高程分带及度日因子数计算方法作为突破点，定量描述流域地形特征对气温空间差异与融雪量造成的影响，解释流域相同海拔上的不同坡向和坡度的气温差异，为流域分带划分，度日因子数及融雪量的计算提供了新方法和思路。

对SRM和基于地形因子改进的SRM模型融雪日径流模拟产生的误差而言，首先融雪径流模型主要用于模拟预报以融雪径流为主的山区流域日径流过程。乌鲁木齐河流域除了融雪产流之外，降水也是主要产流方式之一，对径流的贡献分别为36%和37%[34]，径流组成中对径流的贡献与融雪径流相等，一定程度上不利于以融雪计算为主的SRM模型在该流域径流模拟效果的进一步提高；其次，积雪覆盖序列日资料的计算，MOD 10A2数据每隔8 d有一景图像，部分图像因受云覆盖或新降雪影响无法使用，使得采用的相邻2期MOD 10A2数据的间隔就延长。本文研究可利用的两期相邻数据间隔最长达24 d，在时间上不连续，不利于流域融雪过程的准确描述。选择具有代表性意义的MOD 10A2数据，并在2期MOD 10A2数据之间采用什么样的插值方法来获得连续的积雪信息是融雪径流模型建立过程中需要进一步研究的重要问题；再次，在干旱和半干旱区高山积雪升华作用比较强烈，而融雪径流模型对流域融雪主要考虑由融雪和降雨产生的径流以及它们的相关参数，没有解释径流的地下水补给以及流域截留、入渗、蒸散发和升华等对径流产生的影响；最后，模型参数的估算与流域规模有着一定的联系。一般大流域涵盖着复杂多变的气候分带，与小流域相比，大流域水文气象特征较复杂，参数估算也有着较大的难度，用户对流域特征的认识深度直接影响流域参数的估算是否有效。

5 结 论

利用乌鲁木齐河流域气象台站和水文站的实测资料，基于地形因子改进的SRM模型以流域高程分带及度日因子数计算方法作为突破点，定量解释流域相同海拔上的不同坡向和坡度的气温差异，提出结合海拔、坡向和坡度相结合的流域分带及度日因子数计算方法，由此改进传统SRM模型计算融雪径流。以2007年3—8月为模拟校准期，以2005年和2006年3—8月为模拟验证期，建立数据稀缺流域传统和基于地形因子改进的融雪径流改进模型，结果表明，模型改进后，乌鲁木齐河流域春夏季3 a平均2由0.77提高到0.80，而3 a平均RMSE 值由5.70 m3/s降低到5.35 m3/s，减少了径流量模拟值和实测值的差异，在融雪径流模拟中具有更好的模拟效果。

在数据稀缺干旱流域以模型变量的正确估算及有效的参数率定为前提，结合坡向和坡度可以改进融雪径流模拟效果，在一定程度上显示其提高模拟精度的潜力。本文研究首次把基于地形因子改进的SRM模型应用到乌鲁木齐河流域，为数据稀缺干旱流域的融雪径流模拟提供新的思路和方法。在今后的工作中，把改进后的模型推广应用到中国西北干旱区的冰雪融水径流模拟中，由此进一步验证该模型的适用性和优越性。

[1] Abudu S, Cui C, Saydi M, et al. Application of snowmelt runoff model (SRM) in mountainous watersheds: A review[J]. Water Science and Engineering, 2012, 5(2): 123－136.

[2] 穆艾塔尔·赛地，丁建丽，阿不都·沙拉木，等. 天山北坡山区流域融雪径流模拟研究[J]. 干旱区研究，33(3)：636－642. Muaitaer·Saidi, Ding Jianli, Abudu·Shalamu, et al. Simulation of snowmelt runoff in the catchments on northern slope of Tianshan mountains[J]. Arid Zone Research, 2016, 33(3): 636－642. (in Chinese with English abstract).

[3] 穆艾塔尔·赛地，阿不都·沙拉木，崔春亮，等. 新疆天山北坡山区流域水文特征分析[J]. 水文，2013，33(2)：87－92. Muaitaer·Saidi, Abudu·Shalamu, Cui Chunliang, et al. Hydrological characteristics of typical watersheds in north Tianshan [J]. Journal of China Hydrology, 2013, 33(2): 87－92. (in Chinese with English abstract).

[4] 马虹，程国栋. SRM融雪径流模型在西天山巩乃斯河流域的应用实验[J]. 科学通报，2003，48(19)：2088－2093. Ma Hong, Cheng Guodong. A test of snowmelt runoff model (SRM) for the Gongnaisi River basin in the western Tianshan Mountains, China[J]. Chinese Science Bulletin, 2003, 48(19): 2088－2093. (in Chinese with English abstract).

[5] Abudu S, Cui C, King J P, et al. Comparison of performance of statistical models in forecasting monthly streamflow of Kizil River, China[J]. Water Science and Engineering, 2010, 3(3): 269－281.

[6] 张璞，王建，刘艳，等. SRM模型在玛纳斯河流域春季洪水预警中的应用研究[J]. 遥感技术与应用，2009，24(4)：456－461. (in Chinese with English abstract). Zhang Pu, Wang Jian, Liu Yan, et al. Application of SRM to flood forecast and forwarning of Manasi River basin in spring [J]. Remote Sensing Technology and Application, 2009, 24(4): 456－461.

[7] Hock R. Temperature index melt modelling in mountain areas[J]. Journal of Hydrology, 2003, 282: 104－115.

[8] Kang K, Merwade V. Development and application of a storage－release based distributed hydrologic model using GIS[J]. Journal of Hydrology, 2011, 403(1): 1－13.

[9] 蒋熹，王宁练，贺建桥，等. 山地冰川表面分布式能量-物质平衡模型及其应用[J]. 科学通报，2010，55(18)：1757－1765. Jiang Xi, Wang Ninglian, He Jianqiao, et al. A distributed surface energy and mass balance model and its application to a mountain glacier in China[J]. Chinese Science Bulletin, 2010, 55(18): 1757－1765. (in Chinese with English abstract).

[10] Pellicciotti F, Brock B, Strasser U, et al. An enhanced temperature -index glacier melt model including the shortwave radiation balance: Development and testing for Haut Glacier d ′Arolla, Switzerland [J]. Journal of Glaciology. 2005, 51(175): 573－587.

[11] Hock R. A distributed temperature-index ice and snowmelt model including potential direct solar radiation [J]. Journal of Hydrology, 1999, 45(149): 101－111.

[12] Kondo J, Yamazaki T. A Prediction model for snowmelt, snow surface temperature and freezing depth using a heat balance method[J]. Journal of Applied Meteorology, 1990, 29: 375－384.

[13] Li X G, Williams M W. Snowmelt runoff modeling in an arid mountain watershed, Tarim Basin, China[J]. Hydrological Processes, 2008, 22(19), 3931－3940.

[14] 王建，沈永平，鲁安新，等. 气候变化对中国西北地区山区融雪径流的影响[J]. 冰川冻土，2001，23(1)：28－33. Wang Jian, Shen Yongping, Lu Anxin, et al. Impact of climate change on snowmelt runoff in the mountainous regions of Northwest China[J]. Journal of Glaciology and Geocryology. 2001, 23(1): 28－33. (in Chinese with English abstract).

[15] 张一驰，李宝林，包安明，等. 开都河流域融雪径流模拟研究[J]. 中国科学: 地球科学，2006，36(A02)：24－32. Zhang Yichi, Li Baolin, Bao Anming, et al. Simulation of snowmelt runoff model in Kaidu River basin[J]. Science in China Series D: Earth Sciences, 2006, 36(A02): 24－32. (in Chinese with English abstract).

[16] 刘俊峰，杨建平，陈仁升，等. SRM融雪径流模型在长江源区冬克玛底河流域的应用[J]. 地理学报，2006，61(11)：1149－1159. Liu Junfeng, Yang Jianping, Chen Rensheng, et al. The simulation of snowmelt runoff model in the Dongkemadi River basin, headwater of Yangtze River[J]. Acta Geographica Sinica, 2006, 61(11): 1149－1159. (in Chinese with English abstract).

[17] 卿文武，陈仁升，刘时银，等. 两类度日模型在天山科其喀尔巴西冰川消融估算中的应用[J]. 地球科学进展，2011，26(4)：409－416. Qing Wenwu, Chen Rensheng, Liu Shiyin, et al. Research and application of two kinds of temperature-index model on the Koxkar Glacier[J]. Advance in Earth Science, 2011, 26(4): 409－416. (in Chinese with English abstract).

[18] 张勇，刘时银，丁永建. 中国西部冰川度日因子的空间变化特征[J]. 地理学报，2006，61(1)：89－98. Zhang Yong, Liu Shiyin, Ding Yongjian. Spatial variation of degree-day factors on the observed glaciers in western China[J]. Acta Geographica Sinica, 2006, 61(1): 89－98. (in Chinese with English abstract).

[19] 穆振侠，姜卉芳. 2001年至2010年昆马力克河流域积雪时空变化特性分析[J]. 资源科学，2013，35(1)：148－156. Mu Zhenxia, Jiang Huifang. Spatial and temporal characteristics of snow cover in the Kunmalike river basin[J]. Resources Science, 2013, 35(1): 148－156. (in Chinese with English abstract).

[20] Martinec J, Rango A, Roberts R T. Snowmelt Runoff Model (SRM) User’s Manual [M]. NewMexico: New Mexico State University Press, 2008.

[21] Kang D H. Distributed Snowmelt Modeling with GIS and Casc2d at California Gulch, Colorado[D]. Fort Collins, Colorado: Colorado State University, 2005.

[22] Kang K, Lee J. Hydrologic modelling of the effect of snowmelt and temperature on a mountainous watershed[J]. Journal of Earth System Science, 2014, 123(4), 705－713.

[23] 袁喆，杨志勇，史晓亮，等. 灰色微分动态自记忆模型在径流模拟及预测中的应用[J]. 水利学报，2013(7)：791－799. Yuan Zhe, Yang Zhiyong, Shi Xiaoliang, et al. Differential hydrological gray self-memory model for runoff simulation and prediction[J]. Journal of Hydraulic Engineering, 2013(7): 791－799. (in Chinese with English abstract).

[24] 胡汝骥. 中国天山自然地理[M]. 北京：中国环境出版社，2004.

[25] 张学文，张家宝. 新疆气象手册[M]. 北京：气象出版社，2006.

[26] Rango A, Martinec J. Accuracy of snowmelt runoff simulation[J]. Nordic Hydrology, 1981, 12: 265－274.

[27] Martinec J, Rango A. Parameter values for snowmelt runoff modelling[J]. Journal of Hydrology, 1986, 84(3): 197－219.

[28] Boudhar A, Hanich L, Boulet G, et al. Evaluation of the snowmelt runoff model in the Moroccan High Atlas Mountains using two snow-cover estimates[J]. Hydrological Science Journal, 2009, 54(6): 1094－1113.

[29] Nagler T, Rott H, Malcher P, et al. Assimilation of meteorological and remote sensing data for snowmelt runoff forecasting[J]. Remote Sensing of Environment, 2008, 112(4): 1408－1420.

[30] Tekeli A E, Akyurek Z, Şorman A A, et al. Using MODIS snow cover maps in modeling snowmelt runoff process in the eastern part of Turkey[J]. Remote Sensing of Environment, 2005, 97(2): 216－230.

[31] 黄慰军，黄镇，崔彩霞，等. 新疆雪密度分布研究[J]. 中国农业气象，2007，28(4): 383－385. Huang Weijun, Huang Zhen, Cui Caixia, et al. A study on temporal and spatial distribution of snow density in Xinjiang, China[J]. Journal of Agrometeorology, 2007, 28(4): 383－385. (in Chinese with English abstract).

[32] 黄慰军，黄镇，崔彩霞，等. 新疆雪密度时空分布及其影响特征研究[J]. 冰川冻土，2007，29(1)：66－71. Huang Weijun, Hhuang Zhen, Cui Caixia, et al. Temporal and spatial distribution of Snow density and its characteristics in Xinjiang [J]. Journal of Glaciology and Geocryology, 2007, 29(1): 66－71. (in Chinese with English abstract).

[33] 杨大庆，张黄生，张志中. 乌鲁木齐河源雪密度观测研究[J]. 地理学报，1992，42(3): 260－266. Yang Daqing, Zhang Huangsheng, Zhang Zhizhong. A study on the snow density in the head area of Urumqi River basin [J]. Acta Geographica Sinica, 1992, 42(3): 260－266. (in Chinese with English abstract).

[34] 古丽巴哈·扎依提，迪丽努尔·阿吉. 乌鲁木齐河流域水文特性分析[J]. 枣庄学院学报，2010，27(5)：131－136. Gulbahar·Zayit, Dilnur·Aji. Analysis On the Hydrological Characteristics in theUrumqi River Basin[J]. Journal of Zaozhuang University, 2010, 27(5): 131－136. (in Chinese with English abstract).

穆艾塔尔·赛地，丁建丽，崔春亮. 基于地形因子改进融雪径流的模拟及验证[J]. 农业工程学报，2017，33(19)：179－186. doi：10.11975/j.issn.1002-6819.2017.19.023 http://www.tcsae.org

Muattar·Saydi, Ding Jianli, Cui Chunliang. Simulation and validation of enhanced snowmelt runoff model with topographic factor[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 179－186. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.19.023 http://www.tcsae.org

Simulation and validation of enhanced snowmelt runoff model with topographic factor

Muattar·Saydi1,2, Ding Jianli1,2※, Cui Chunliang3

(1.830046,; 2.830046,;3.830049,)

Snowmelt runoff is an important component of streamflow in the arid and semi-arid watersheds. It is often simulated by a snowmelt runoff model (SRM), an empirical temperature-index model with 3 main variables, such as air temperature, precipitation and snow cover area (SCA) and some additional deterministic parameters describing the basin characteristics. However, the SRM model only considers the effect of elevation on snowmelt and does not consider the effect of aspect and slope on the mountainous area. In order to introduce this model to the Urumqi River basin located at the northern slopes of Tianshan mountain, Xinjiang where the data acquisition was difficult, in this study, we improved the traditional SRM with topographic factor and validated the reliability of the enhanced snowmelt runoff model in simulating the daily runoff. The topographic factors of aspect and slope were introduced in the traditional SRM model. The degree-day factor in the traditional SRM model was improved by adjusted temperature based on aspect and slope. The adjusted values were obtained from previous studies on relationships between air temperature and aspect. Finally, the enhanced SRM included the aspect, slope and elevation. The Urumqi River basin covers an area of 1 073.64 km2, ranges in elevation from 1 683 to 4 459 m with the average elevation of 3 066 m. Three hydro-meteorological stations were available in this region. The watershed was classified into 5 elevation zones for traditional SRM and further into 14 zones by the aspect and slope for the enhanced SRM. Meteorological and hydrological data were collected daily from 3 hydro-meteorological stations located in the watershed, and the SCA was extracted from satellite images of the moderate resolution imaging spectroradiometer (MODIS).The precipitation data from Daxigou station was used to represent the most area of this region based on the relative high correlation between precipitation and runoff. In addition, the data from Yingxiongqiao and Yuejinqiao stations were also included in the low latitude area since the Daxigou station was located in the high elevation area. The degree-day factor and snow runoff coefficient and rain runoff coefficient were obtained for different elevation zones from literatures and empirical formula. The traditional and enhanced SRM models both were used to simulate the daily snowmelt runoff during the snowmelt season of spring and summer in 2007 with limited hydro-meteorological data. For the model validation, the daily runoff for the spring and summer snowmelt seasons from 2005 to 2006 was selected. The results showed that the enhanced models could well simulate daily snowmelt runoff in the mountainous catchments. After including the aspect and slope in the calculation of snowmelt water and numbers of degree-day, the enhanced SRM considering topographic factors performed better than the traditional SRM. The 3-year average of nash-sutcliffe2was increased from 0.77 for the traditional SRM model to 0.80 for the enhanced SRM, and the root mean square error (RMSE) was decreased from 5.7 m3/s for the traditional SRM to 5.35 m3/s for the enhanced SRM. The relative error of the total runoff amount was decreased from 4.17% for the traditional SRM to 2.16% for the enhance SRM. It can be concluded that the enhanced SRM with topographic factors proposed a new method to improve the daily snowmelt runoff simulation with the better performance and has a high potential to simulate snowmelt runoff in an arid mountainous watershed with sparse data.

topography; slope; runoff; aspect; snowmelt; zone; numbers of degree-day

10.11975/j.issn.1002-6819.2017.19.023

P334+.92;TV121+.6

A

1002-6819(2017)-19-0179-08

2017-02-20

2017-07-10

国家自然科学基金项目（41771470、51069017、U1303381）；自治区重点实验室专项基金项目(2016D03001)；新疆大学绿洲生态重点实验室项目（XJDX0201-2013-04）。

穆艾塔尔·赛地，新疆策勒人，博士生，高级工程师，主要从事干旱区水文水资源研究。Email：895798730@qq.com

※通信作者：丁建丽，男，山东人，博士，教授，主要从事干旱区资源环境遥感。Email：watarid@xju.edu.cn