一种结合小世界模型改良的NMF社区发现算法

赵雨露 张曦煌

(江南大学物联网工程学院 江苏 无锡 214122)

一种结合小世界模型改良的NMF社区发现算法

赵雨露 张曦煌

(江南大学物联网工程学院 江苏 无锡 214122)

社区发现是当前复杂网络与数据挖掘的热点，非负矩阵分解是社区发现的常用手段。针对当前非负矩阵分解的社区发现算法，为提高算法的准确率与可解释性，提出多阶邻居节点的概念，在小世界模型的基础上构建了规模可控的多阶复合信息矩阵，用后处理的方法减少了算法中随机因素带来的不稳定性。对于真实网络与人工网络的实验证明，新背景下的算法较原算法在性能上有一定的提升。

社区发现 非负矩阵分解 小世界模型 复杂网络

0 引 言

现实世界中存在大量可以抽象为复杂网络的关系形式，例如人际网络、通信网络和软件中API的调用等。这些网络中包含着大量潜藏的信息，从简单的网络中挖掘和总结出有价值的信息成为既有困难又有意义的工作。

在复杂网络的无标度、高聚集系数和节点中心性等基本特征中，社区结构是一种重要的基本特性。在社区发现的早期研究中，传统的图论与社会学中的层次聚类是主要的研究手段，自2002年NewMan[1]于PNAS上对社区的基本结构提出了更清晰的阐释后，社区结构研究进入全新的层次。针对社团发现的研究大量涌现，研究视角和研究方法也获得了极大丰富，包括渗流、边分割等一系列新视角与新方法。

目前，社区发现的主要手段有图的划分算法、边聚类算法、随机游走、模块度以及层次聚类等。本质上社区发现问题应归纳于无监督学习范畴，非负矩阵分解NMF(nonnegative matrix factorization) 模型作为一种有效的无监督学习手段，也受到了极大关注。研究发现，NMF与K-means和PLSI(probabilistic latent semantic indexing)等无监督学习方法关系密切且具有更好的解释性。将非负矩阵分解应用于对复杂网络中社区的挖掘，具有物理含义明确、计算简单和准确度较高等优点。

NMF是一种有Paatero等[2]提出的矩阵分解思想，直到1999年Lee等[3]将纯数学思想的NMF应用于图像处理并取得良好的成果后，NMF在提取隐含结构与模式时所具有的良好能力才得到重视，之后NMF被广泛应用于诸多领域。其中Wang等[4]提出采用NMF方法对复杂网络进行了社区划分，之后基于非负矩阵的社区发现算法得到了快速发展。众多该领域的学者对其进行了不同程度不同角度的改进。

当前对于基于非负矩阵分解的社区发现算法的主要改良方式主要有替换目标矩阵，例如基于物理过程或以共有邻居结点为依据构造信息矩阵的方法[5-6]、以针对目标矩阵的特殊性进行目标函数优化的方法[7-8]和将更多的先验信息融入信息矩阵的算法[9]等。他们都将基于NMF的社区发现算法发现速度或精度等性能进行了不同程度的提升。

本文权衡算法复杂度提出一种新的信息矩阵，提出一种算法降低NMF带来的随机性，采用真实数据集与人工网络数据集对算法进行实验。

1 预备知识

定义1对于节点v需要最短n条边可以连接的节点，称为节点v的n阶邻居节点。

定义2对于一个无向、无权的图G=(V，E)，V是其所有节点构成的集合，E为其所有连边构成的集合。其邻接矩阵设为A，对于V中的任意节点vi与节点vj之间若存在连边则A[i,j]=1，否则A[i,j]=0。

二十世纪末以来，对通信、社交与技术等网络的研究表明，大多数网络均具有高度的集群性、不均衡的度分布以及中心节点结构等特点。Watts等[10]于1998年发表在nature论文上以数学的方式定义了小世界网络，其中涉及两个重要的衡量网络特征特征路径长度与聚合系数。

定义3网络中，设定连接任意两点所需要的最少边数为两点间的路径长度，全部网络中所有节点间的路径长度的平均值，定义为网络的特征路径长度。其网络节点数量与特征路径长度的关系为：

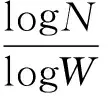
(1)

式中，N为节点总数，W为每个节点的联系宽度，n为特征路径长度。

可以看出随着网络节点数指数增长，平均步长近似线性增长。该文指出，社会关系中人普遍的联系宽度为260，在超过70亿节点的网络中从任一节点联系到另一节点仅需6.5步，即著名的“六度分割理论”。

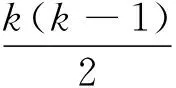
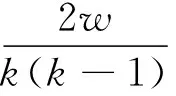
(2)

式中，w为实际的边数，k为节点v的连边个数，cc为节点v的聚合数。网络中所有节点的聚合数的平均值为网络的聚合数。网络的聚合系数反映了相邻两个节点之间的邻居节点的重合程度。

2 基于NMF的社区发现算法改进

2.1 非负矩阵分解与社区发现

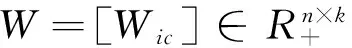
minD(X,WHT)s.t.M≥0H≥0

(3)

式中，D(x,y)为x与y差异性的损失函数，实际应用中D(x,y)可以选用平方误差函数或者广义KL散度函数。

平方误差函数是采用两个矩阵差的Frobenius范数平方表示，即：

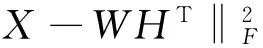
(4)

广义KL散度的定义为：

(5)

然后可以采用多步叠乘、梯度下降或交替最小二乘法等方法对目标函数进行优化。

2.2 一种基于小世界模型的复合多阶信息矩阵

目前绝大多数基于矩阵分解的社区发现算法多采用邻居矩阵作为数据矩阵，通过上节关于对此类算法应用于社区发现的解释可以发现数据矩阵若包含更多连边信息则会更有助于社区发现的质量，而邻接矩阵的缺陷在于只能反映某节点与其一阶邻居节点的关系不能直观地反映与其他更高阶的大多数节点的关系。

为此，本文采用一个三维矩阵M[i][j][l]描述任一节点与绝大多数节点之间形成的关系。i、j分别对应节点vi与节点vj，若两个节点在第l步建立联系，则M[i][j][1]=1；否则M[i][j][1]=0。考虑到矩阵中节点vi到达自身无太多实际意义，所以矩阵M[i][j][1]中的对角线应全为零。

通过小世界模型的特征路径长度概念可以发现，当三维矩阵中的l等于特征路径长度时，就可以将节点i与大多数的节点建立联系。为充分体现边的生成概率，通过多重路径到达的节点应该得到加权，即在第l层有t种路径从节点i到达某节点j，则该节点对应的M[i][j][1]=t。例如，图1中的节点v1到v5对应的M[1][5][2]=2,而v1到v4对应的M[1][2][4]=1。此外，文献[11]指出聚合系数对于社区结构的重要意义，同一节点可以被不同的步长多次访问，则每一次访问都应该被记录以加权体现访问概率，图1中的v1与v2对应的M[1][2][1]=1且M[1][2][2]=1。

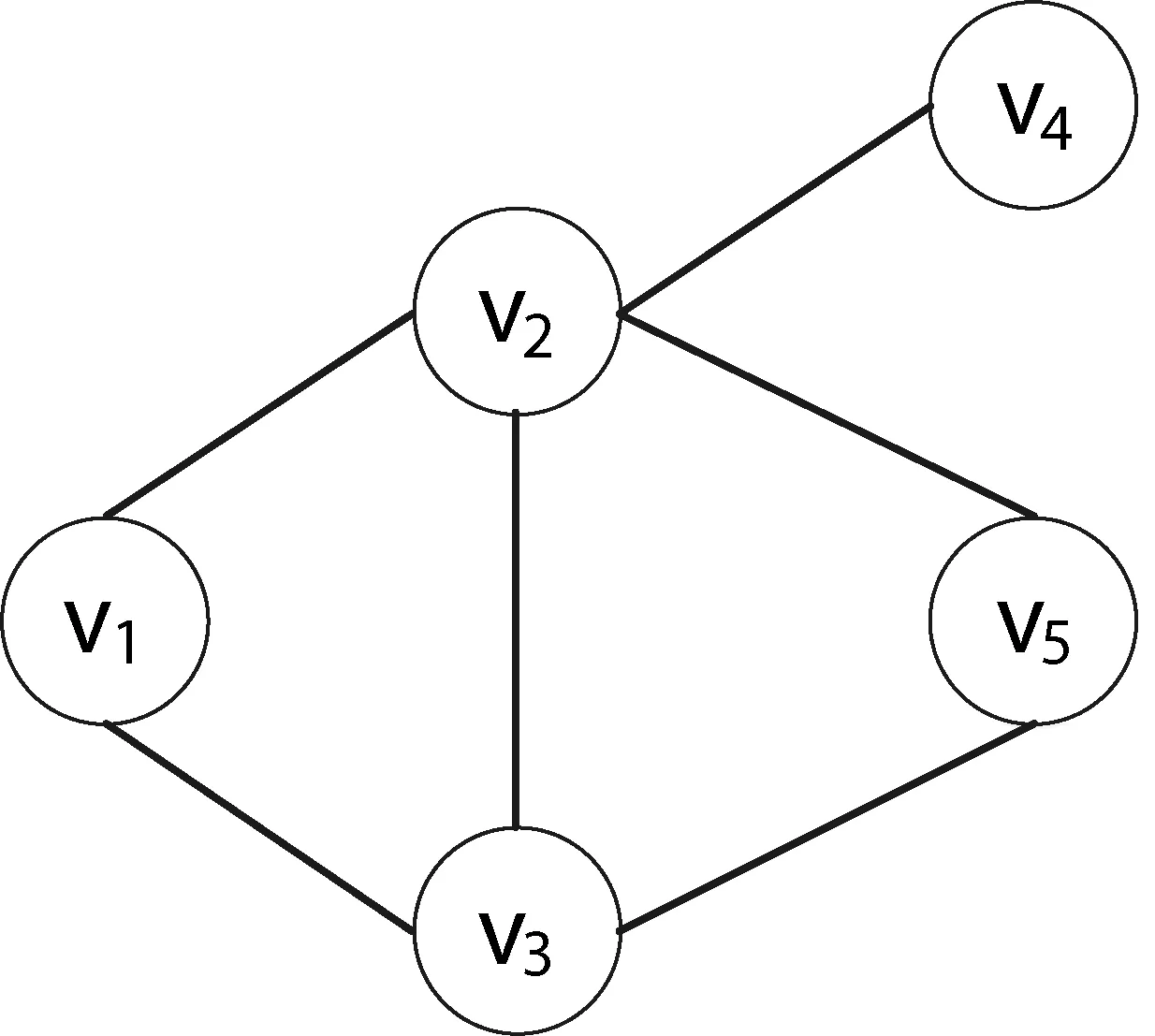
图1 五个节点构成的网络图

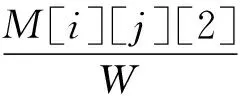
(6)

2.3 目标函数的求解与算法优化

实际应用中，复杂网络的信息矩阵有着一定的特殊性，例如对于共有n个节点的无向复杂网络信息矩阵一般为大小是n×n的对称矩阵，且主对角线全为零。基于此，大量的改良后的非负矩阵分解算法被提出，一种常应用于社区发现的改进非负矩阵分解的方法为文献[12]提出的SNMF算法。被分解后的两个矩阵为对称的大小为n×c的U与UT,SNMF的算法公式如下：

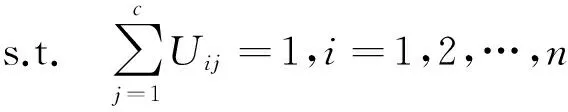
(7)

式中，n为节点的数量，c为社区的数量，Uij表示节点i隶属于社区j的概率。

为了得到矩阵U,可以采用欧氏距离衡量X与UUT的相似度，利用式(8)目标函数进行限定次数的迭代得到结果：

(8)

采用文本中的数据矩阵进行基于非负矩阵分解的社区发现进行多次实验，证明处于两个社区边界的节点会被随机的划分的两个社区中的任一一个，在数据上即表现为分解后的U中前几列差值较小的行数，由此带来了算法的不稳定性。为了提高稳定性，需要对输出的结果进行后处理。本文将利用信息矩阵对边界节点最终划归的社区进行判定。基本思路为，利用信息矩阵统计已经确定的社区中所有节点对于该边界节点的影响力之和，再取平均值，最后将节点划归平均值较大的社区内，其可表达为：

(9)

2.4 改进后的SNMF-sl算法描述

综上可以得到新的基于矩阵分解的社区发现算法，其步骤如下：

输入：邻接矩阵A，迭代次数T，划分成c个社区

输出：节点社区划分矩阵E

步骤1对邻接矩阵A进行处理，统计并计算出节点总数N，节点平均联系宽度W，特征路径长度1。

步骤2构造l阶的三维矩阵M。

步骤3通过式(6)进行处理后得到二维数据矩阵Γ。

步骤4按照式(8)迭代计算U矩阵(共迭代T次)，并对W进行归一化操作，使得W矩阵每一行元素之和为1。

步骤5筛选出U中隶属度差值较小的节点，并利用式(9)对最后结果进行后处理。

步骤6输出结果U。

2.5 算法复杂度分析

步骤1需要时间复杂度O(n)，步骤2需要时间复杂度O(nl)，步骤3的复杂度为O(n)，步骤4需要复杂度O(Tn2c)，若边界上未确定的节点总数为s平均带分入的社区数量为q社区平均节点数量为p则步骤4复杂度为O(sqp)。综上算法所需要的总复杂度为O(nl+Tn2c)。

3 基于非负矩阵分解的社区发现算法改进

3.1 实验数据集与评估方法

为了有效地测试对比改进后的算法与原算法，我们将分别采用真实数据集与人工网络数据集对算法分别进行测试，并采用相关指标量化两种算法的划分性能。所有实验均采用MATLAB实现，为了保证公平性，所有的数据矩阵都将使用同样的软件与硬件环境，目标函数变化小于e-10为终止条件，运行20次取平均值。

数据集Zachary Karate Club[13]是一个著名的复杂网络小型数据集，其包含34个节点，78条边。后来该俱乐部由于管理问题，该网络被分为两个大小相当的子社区。

Dolphin Social Network是由Lesseau等[14]用近七年时间对新西兰一海湾的宽吻海豚进行观察实验收集后得到的关系网络，其包含62个节点共有159条边，大致分为两个社区，亦是常用于社区发现的数据集之一。

American College football Network由美国2000年橄榄球赛季的高校代表队组成，网络中的连边表示橄榄球队之间进行过比赛。其一共包含115个节点，613条边构成，115个代表队来自12个联盟。

Books about US politics网络中，节点表示美国亚马逊在线售卖的书籍，若两本书被同一个顾客购买则两个节点之间建立起连边。一共包含105个节点，441条连边，可以大致分为三个不同的类型即三个社区。人工网络数据集采用Lancichinetti等[15]人提出的LFR benchmark，其可以生成指定规模不同需求的网络数据集，生成网络输入数据中一个重要的参数为混合参数mu。mu表示节点与社区外部节点链接的概率，mu值越大生成数据的社区之间的边界越模糊，mu值越小生成社区之间的边界越清晰。

为了方便比较几个算法的性能，本文采用标准互信息与准确率作为量化的评价方法。

(1) 精准率(ACC)

给定节点vi，lpi为该节点被社区划分的结果，lti为其实际所在的社区编号。精准率的实际意义为所有被划分节点中占正确节点的总数，根据文献[16]精准度的数学定义如下：

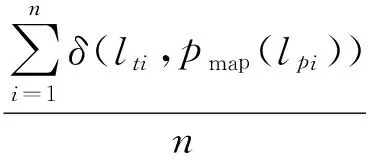
(10)

式中，对于函数δ(x,y)，当x=y时，函数值为1否则为0。pmap(lpi)为映射函数用以调取节点vi对应的社区编号。N为节点总数。ACC值的取值在0到1之间，越大说明社区划分的准确率越高，反之则准确率越低。

(2) 标准互信息(NMI)

标准互信息是一种由Lancichinetti等[17]提出的一种公认较为可靠的评估标准。其可以量化算法生成的结果与标准社区结构的相似程度，以方便进行评价比较。数学定义如下：

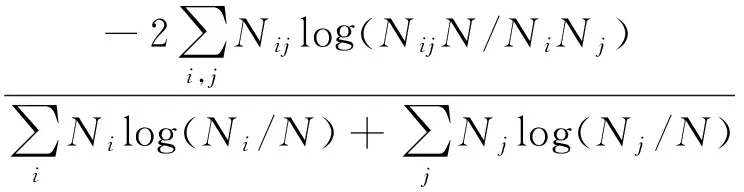
(11)

式中，N为含混矩阵，Nij代表i、j两个社区中共有的节点个数，而Ni、Nj分别表示N中对应的第i、j行的和。通过式(11)可知，NMI的取值范围处于0到1之间。NMI越小说明与标准网络区别越大，NMI越大说明与标准网络越相似。

3.2 实验与结果分析

为了比较文中提及的数据矩阵与后处理改进对社区划分结果的影响。将要以SNMF为基本方法分别以邻接矩阵A，基于物理过程的热量扩散得到的方法(heat)[5]，基于最共邻节点数量为依据的jaccard相似度方法[18]方法与本文提及的小世界模型下的多阶复合矩阵(sl)为信息矩阵进行非负矩阵分解。选用文中提及的四个真实数据集进行实验。真实网络结构并不一定完全符合完美的社区结构模型，故对真实的网络结构使用精准率作为评价指标。

表1的实验结果中，较邻接矩阵而言，各类新矩阵在基于NMF的社区划分中取得了更好的实验结果，说明矩阵中更为丰富的信息有利于提升社区划分的精度，而本文提出的新矩阵sl方法从基于NMF社区发现的物理解释出发构造，划分结果较其他算法更优。

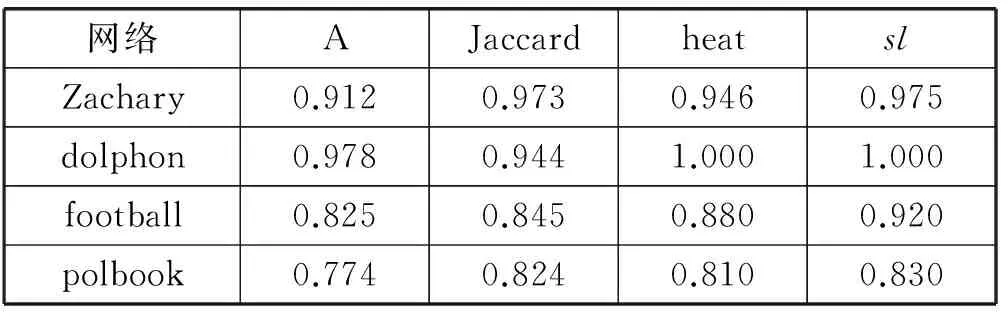
表1 采取不同数据矩阵的准确率比较

为了考察后处理对于社区划分结果稳定性的影响，本文采用人工网络LFR。其中LFR的数据设置如表2所示，这里，mu取值范围是0.35到0.8，每次递增0.05生成10个边界清晰程度不同的LFR-4000网络。

表2 LFR-4000人工网络参数设置

图2中记录的是在LFR-4000人工网络下，各种不同情况下NMI值的变化。

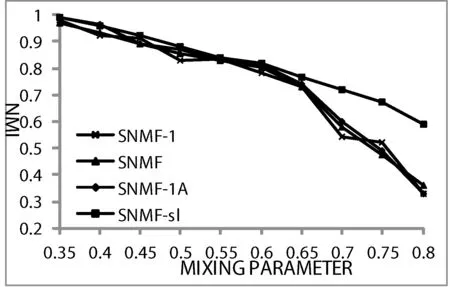
图2 不同实验条件下LFP-4000网络上NMI值比较

图中折线SNMF-1为采用SNMF算法随机的一次划分的NMI值结果，SNMF-1A为采用后处理后的SNMF算法开始随机的一次划分的NMI值结果，SNMF为运行算法20次的平均结果，SNMF-sl为采用了sl信息矩阵与后处理后运行20次的平均结果。

从以上的实验结果来看，sl方法得到的信息矩阵较其他类型的矩阵体现了更多的有用信息，令算法的精准率获得了提高。而新的后处理手段，尤其在社区边界不清晰的情况下使算法的结果趋于稳定，并且使得算法获得了更好的社区划分结果。值得注意的是，在人工网络的实验中当社区边界清晰时，改良后的算法与先前的算法并没有多少性能上的差异，但是当边界逐渐模糊发现社区难度变大时，改良后的算法优势更为明显，具有更好的适应性。

4 结 语

本文的实验结果表明，在矩阵分解的社区发现算法中，通过采用本文的信息矩阵与后处理方法，可以提高划分结果的精准性，同时提高算法结果的稳定性，可以有效降低运算次数。虽然通过小世界模型，控制了生成新信息矩阵的复杂度，但生成的矩阵不再是邻接矩阵，并且生成矩阵的复杂度依然很高。所以在以后的工作中，需要通过并行计算的实现方法提高算法的效率，使得本文算法更有利于应用。

[1] Newman M E J.The Structure and Function of Complex Networks[C]//SIAM Rev,2006:167-256.

[2] Paatero P,Tapper U.Positive matrix factorization:A non-negative factor model with optimal utilization of error estimates of data values[J].Environmetrics,1994,5(2):111-126.

[3] Lee D D,Seung H S.Learning the parts of objects by non-negative matrix factorization[J].Nature,1999,401(6755):788-791.

[4] Wang F,Li T,Wang X,et al.Community discovery using nonnegative matrix factorization[J].Data Mining and Knowledge Discovery,2011,22(3):493-521.

[5] Mahajan S,Pande A,Pande S,et al.Mining Web Graphs for Recommendations[J].International Journal of Electronics Communication and Computer Engineering,2014,5(2):351-353.

[6] Jiao J,Hu D,Zhang Z Y.A Novel Similarity Measurement for Community Structure Detection[C]//International Conference on Intelligent Human-Machine Systems and Cybernetics,2012:301-306.

[7] Staff P O.Correction: uncovering community structures with initialized bayesian nonnegative matrix factorization[J].Plos One,2014,9(9):e107884-e107884.

[8] Cao X,Wang X,Jin D,et al.ERRATUM:Identifying overlapping communities as well as hubs and outliers via nonnegative matrix factorization[J].Scientific Reports,2014,3(10):2993-2993.

[9] Zhang Z Y,Sun K D,Wang S Q.Enhanced Community Structure Detection in Complex Networks with Partial Background Information[J].Scientific Reports,2013,3(11):48005.

[10] Watts D J,Strogatz S H.Collective dynamics of ’small-world’ networks[C]//Nature,1998:440-442.

[11] Cui Y,Wang X,Li J.Detecting overlapping communities in networks using the maximal sub-graph and the clustering coefficient[J].Physica A Statistical Mechanics & Its Applications,2014,405(405):85-91.

[12] Xu J,Xiang L,Wang G,et al.Sparse Non-negative Matrix Factorization (SNMF) based color unmixing for breast histopathological image analysis[J].Computerized Medical Imaging & Graphics the Official Journal of the Computerized Medical Imaging Society,2015,46 Pt 1:20-29.

[13] Newman M E.Fast algorithm for detecting community structure in networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2004,69(6):066133.

[14] Lusseau D,Schneider K,Boisseau O J,et al.The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations[J].Behavioral Ecology and Sociobiology,2003,54(4):396-405.

[15] Lancichinetti A,Fortunato S,Radicchi F.Benchmark graphs for testing community detection algorithms[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2008,78(4 Pt 2):561-570.

[16] Li Y,Jia C,Yu J.A parameter-free community detection method based on centrality and dispersion of nodes in complex networks[J].Physica A Statistical Mechanics & Its Applications,2015,438:321-334.

[17] Lancichinetti A,Fortunato S,Kertész J.Detecting the overlapping and hierarchical community structure of complex networks[J].New Journal of Physics,2009,11(3):19-44.

[18] Zachary W W.An Information Flow Model for Conflict and Fission in Small Groups[J].Journal of Anthropological Research,1977,33(4):473.

ACOMMUNITYDETECTIONALGORITHMBASEDONSMALLWORLDMODELANDNMF

Zhao Yulu Zhang Xihuang

(SchoolofInternetofThingsEngineering,JiangnanUniversity,Wuxi214122,Jiangsu,China)

Community detection is the hotspot of current complex networks and data mining, whose common means is non-negative matrix factorization. To improve the accuracy and interpretability of community detection algorithm, we propose the concept of first-order neighbors. On the basis of the small-world model, this paper constructed a controllable scale multi-stage compound information matrix. Treatment reduced the algorithm after using random factors of instability. Regarding experimental proof of the real network and artificial networks, new algorithms increase in performance compared to the original algorithm.

Community detection Non-negative matrix factorization Small-world model Complex network

TP301.6

A

10.3969/j.issn.1000-386x.2017.10.048

2016-11-27。江苏省产学研合作项目(BY2015019-30)。赵雨露，硕士生，主研领域：数据挖掘。张曦煌，教授。