互相关直径测量的相位跟踪采样控制与校正

杨泽林 何云祥 何 莉

1(重庆理工大学电气与电子工程学院 重庆 400054)

2(綦江齿轮传动有限公司计量中心 重庆 401421)

互相关直径测量的相位跟踪采样控制与校正

杨泽林1何云祥2何 莉1

1(重庆理工大学电气与电子工程学院 重庆 400054)

2(綦江齿轮传动有限公司计量中心 重庆 401421)

为了提高互相关法直径测量的精度，需要对工件表面误差信号进行等相位间隔跟踪整周期采样。介绍分频法实现相位跟踪采样控制的原理；对相位间隔准确度的影响进行了讨论，提出固有误差和随机误差的概念，对其产生原因进行了分析；引入附加角测量环节对采样相位间隔进行校正，给出校正算法；结合ARM7 LPC2148 MCU嵌入式系统，介绍相位跟踪采样控制、校正测量及同步的具体实现。实验测试表明：转速频率波动大于千分之一，采样控制系统的分频系数即会发生改变，相位跟踪性良好；在3 000转/分以下，采样相位间隔误差控制在0.001 13度以内；证明附加角测量和采样相位间隔校正是必要的。

直径测量 互相关原理 嵌入式系统 相位跟踪采样 校正

0 引 言

随着对产品技术指标要求的提高，现场质量控制由抽检转变为每件必检，由单指标转变为多指标，因此需要新的在线检测方法及技术装置。直径是圆形工件的最基本参数，通常通过量具人工测量，而圆度则由计量室定期抽检，用专用仪器测量，显然不能满足生产现场质量控制需求。CCD光学图像法[1]可以同时测量直径和圆度，但对工件表面及工作环境要求较高，测量精度较低且对于锥形工件测量困难；Taylor Hobson-265圆柱度仪利用单测头对工件表面进行旋转扫描，可以精密测量圆度，通过组合法也可以间接测量直径，但严格要求测头移动轨迹通过圆心，且工件与仪器转台要保证很高同心度和同轴度。所以装夹调整时间过长，测量效率极低，也不能用于现场质量控制。上述方法测量原理直观，但均属于静态局部的测量，没有全面客观地反映圆形工件的直径等参数。

利用互相关原理对回转工件两路表面误差信号进行动态测量处理，可以高精度地测量圆形工件的内(外)直径。并可同时测量圆度和锥度等多种参数，不需要苛刻的测量条件而且速度快，非常适合生产现场的在线测量与质量控制。其原理是通过提取两路信号的相位差及其对应的弦长而求取直径，其中相位差的精度是保证直径测量精度的关键。互相关法是目前测量相位差应用较多的一种方法[2-5]，采样控制分为非整周期采样和整周期采样。非周期采样只需按等时间间隔采样一组数据即可，采样控制简单准确，但算法复杂，对采集数据段有绝对零点的要求。因此需对数据作预处理，在利用零相位滤波器提取基频信号周期时会出现误差，导致相位差的测量出现误差[6-7]。整周期采样是按照等相位间隔Δφ=2π/N采样一个或多个周期数据，作离散频谱等分析时，分析谱线落在振动信号的频率上，从而获得比较准确的频谱定位。避免频谱泄漏和栅栏效应对频谱分析精度的影响，也使离散相关函数谱线定位没有误差，亦可准确测量相位差，而且算法简单，使用约束条件少[8-10]。但严格要求采样间隔Δφ的准确度且不能随信号周期或转速的波动而改变，应有很好的相位跟踪性能，采样控制实现困难。

在机械回转运动分析测量中，由于提供了转速参考信号，相比通信、电力电子和流量等测量较容易实现整周期等相位间隔采样，如用圆光栅、锁相环和时钟分频法[11]等提供采样控制信号。圆光栅旋转时即可输出等相位间隔采样控制信号而且相位跟踪特性很好，但需要安装在回转轴上，适用于专用测量系统。锁相环利用鉴相压控震荡原理对转速参考信号倍频产生采样控制信号，如果参考信号不稳定，特别是低频时，相位跟踪实时性较差[12]，锁相范围小，电路复杂。分频法可利用定时/计数器通过软件方便实现，而且相位间隔改变灵活，跟踪范围宽，实时性好，但相位间隔准确度较差。以嵌入式系统ARM LPC2148 MCU为硬件基础，利用其丰富的定时/计数器资源，实时跟踪测量转速，对时钟分频实现相位跟踪采样控制，产生等相位间隔采样控制信号。并对相位间隔Δφ的误差进行分析，提出了相位间隔Δφ准确度的校正方法及相应的相位跟踪采样控制系统，提高Δφ的准确度，保证直径测量精度。以此开发的测量系统已成功应用于重卡变速箱一轴内追孔加工过程的锥度在线自动测量与质量控制[13]。

1 测量算法原理

互相关测量直径的原理如图1所示。W3为光电转速传感器，每转输出一个转速脉冲，W1、W2为激光位移传感器。被测工件以O为圆心旋转时，W1、W2测出弦长L(θ)，同时输出被测圆的表面回转误差信号X(θ)和Y(θ)。X(θ)、Y(θ)是被测圆同一截面的表面回转误差信号，因此X(θ)、Y(θ)具有很强的相关性，X(θ)、Y(θ)的互相关函数为：

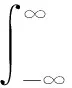
(1)

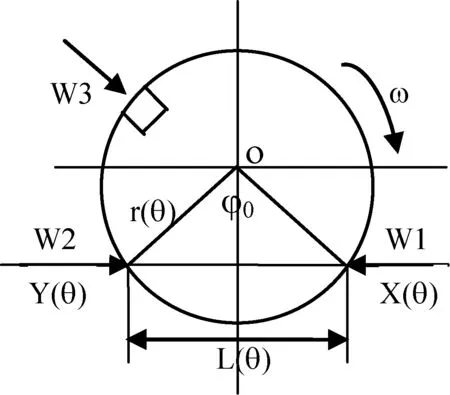
图1 互相关直径测量原理图

由互相关理论可知：互相关函数曲线的最大峰值所在点为Y(θ)，相对X(θ)相位延迟角度φ0，亦为图1中弦长对应的圆心夹角φ0，根据直角三角形的边角关系，得到圆的直径：

d(θ)=L(θ)/sin(φ0/2)

(2)

所有函数均以相位为参考变量，因此，应对信号X(θ)和Y(θ)按等相位间隔采样，利用离散傅里叶变换(DFT)求得离散互功率谱Sxy(n)。再进行离散傅里叶反变换(DFT-1)，即可得到基于相位延迟或者X(θ)与Y(θ)相位差的离散互相关函数Rxy(k)[14]，从而求得图1中相位差φ0：

Rxy(k)=K×DFT-1[Sxy(n)]

(3)

φ0=n×Δφ

(4)

其中，n为φ0在Rxy(k)中的位置序号，Δφ为离散相关函数相位差分辨率。根据离散傅里叶变换理论，频谱函数的频率分辨率：

(5)

其中fs为采样频率,Δt为采样时间间隔，N为采样数据段点数，T为采样数据段时间长度。对于回转运动，引入转速参量ω，取采样数据长度T为一个旋转周期，则有：

(6)

可见，Δφ既是按角度采样的角度间隔，又是互相关函数Rxy(k)的相位差分辨率。如果严格按照式(5)产生采样控制信号，保证Δφ准确，则相位差φ0和直径的精度可以得到保证，否则弦长对应的圆心夹角φ0会产生误差，而且会随着式(4)中n的变化而累积。

2 分频法相位跟踪采样控制与误差分析

2.1 分频法相位跟踪采样控制原理

分频法相位跟踪采样控制原理[15]如图2中(a)所示，根据定时0测量得到的转速信号频率fT，利用MCU的计数器2对系统时钟fclk分频，输出采样控制信号fAD，并使fAD=N×fT。

图2 控制和校正测量原理图

首先，确定每个旋转周期的采样点数N，定时器0测量转速频率fT，根据式(7)计算分频器的分频系数M：

M×N×fT=fclk

(7)

将求得的分频系数M下载到分频器中，对时钟信号M分频，即可得到相位跟踪采样控制信号fAD。信号fclk、fT、fAD它们的波形及相互关系如图3-图6所示。

图4 转速信号fT波形

图5 相位跟踪控制信号fAD波形

图3 时钟信号fclk波形

图6 同步相位跟踪信号fAD波形

2.2 误差分析

在测量过程中除图1和式(2)中弦长的测量误差，圆度形状误差外，由于将采样控制由时间间隔换算成相位间隔、转速波动、计数器位数和时钟速度等因素，使得采样相位间隔不满足式(6)的要求而产生采样误差，是直径测量产生误差的一个关键原因。这使得采样数据段不是严格的整周期采样，出现截断效应使离散互相关函数的谱线出现泄漏和栅栏效应，谱线位置产生偏移。作为相位差φ0计量单元的离散相位谱线分辨率Δφ的值将不准确，对直径测量精度的影响最显著。因此，Δφ的准确度对测量精度尤为重要。

2.2.1 固有误差

理论上，对于任何转速、采样点数与系统时钟，分频法实现相位跟踪采样的基础原理表达式(7)是很难成立的，即求取分频系数M时不能整除，使Δφ≠2π/N而产生了误差，称此误差为分频法Δφ的固有误差。

2.2.2 随机误差

在实际的应用中，分频系数M是根据前一转甚至前几转的转速预测计算得到的[16]。虽然有较好的相位跟踪实时性，但仍不能很好地契合当前转速，完全满足式(7)的要求，同样会使Δφ偏离2π/N而产生误差。在转速不稳的工况下，其误差会更大，称此误差为分频法Δφ的随机误差。

因为上述两个产生误差的原因，使得相位跟踪采样控制信号相对于转速信号，在没有同步的情况下，在一个旋转周期，出现了Δθ1和Δθ2两个随机附加角，分布在每一个采样数据段的头尾，如图5所示，总的附加角为Δθ1+Δθ2，且不等于Δφ，因此不能保证Δφ=2π/N，使Δφ不准确，从而影响相位差φ0和直径的测量精度。由于Δθ1的随机性，使第一个采样数据相对转速参考信号的相位不确定，会给分析结果增加一个随机初始相位偏移，不仅使φ0的定位出现错位，而且由于式(4)累积效应使φ0出现误差。

3 采样相位间隔校正及实现

为了消除固有误差和随机误差对采样间隔Δφ准确度的影响，在分频法相位跟踪采样控制系统中增加同步功能，使Δθ1=0。利用定时器1增加一个测量环节，将转速信号fT和采样控制信号fAD输入到它的捕获端，测量出当前转的Δθ2，对Δφ的准确度进行校正，得到客观准确的Δ′φ，校正后的Δ′φ为：

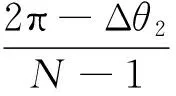
(8)

ARM7 LPC2148 MCU具有三个功能完全相同的定时/计数器硬件模块，互不关联，可以独立运行，不受CPU的控制。利用它们各自完成转速测量、相位跟踪采样控制与校正：将每次开始采样的第一个ADC启动脉冲与转速脉冲同步，使Δθ1=0，将附加角全部集中在Δθ2中，其时序波形如图6所示。1) 定时/计数器0实现转速测量、采样及其同步控制：开始采样后的第一个转速信号fT的上升沿清零分频器，将计算的分频系数M装入分频器，置fAD信号为高电平，使信号fAD与信号fT上升沿同步，即Δθ1=0，同时启动分频器对时钟信号fclk(60 MHz)进行M分频，输出相位跟踪采样控制信号fAD；2) 定时器1测量附加角Δθ2：fAD的上升沿清零并启动定时器1，对时钟信号fclk计数，转速信号fT上升沿停止定时器1，结束采样的转速信号fT上升沿时刻，定时器1的计数值则为Δθ2。实现了同步整周期采样和附加角Δθ2测量，Δθ2的测量控制原理如图2中(b)所示。

4 实验测试与结果

实验测试在直径测量系统上进行，主要目的是观察分频系数M、实际相位间隔Δ′φ随转速变化的响应，以检验分频法相位跟踪采样控制的跟踪性能，Δφ的校正效果与同步功能。用dg1022u信号发生器产生转速信号fT，用dso_x 2012a示波器观察fAD、fT的波形及同步关系，参数M和Δ′φ通过MCU串口输出，PC机串口助手软件接收并显示。取N=128和N=256，在fT=9.99～10.01 Hz和49.95～50.05 Hz范围各取三点进行测试。测试结果如表1所示，fAD、fT波形如图7所示。

表1 M,Δθ2,Δ′φ测试结果

图7 fAD、fT实测波形图

图7表明fAD、fT实现了同步，Δθ1=0，稳定了采样数据段的初始相位。无论是高转速或低转速段，N=128或N=256，千分之一的转速波动，均会引起分频系数M的改变，说明分频法能够很好地宽范围地跟踪响应转速波动。测控软件和定时器1能灵敏地测量出附加角Δθ2和校正Δφ，采样间隔误差Δφ-Δ′φ控制在0.001 13度以内。但随着转速的增加，分频系数M对转速波动的响应会减弱，这可以通过提高系统时钟频率加以改善。

5 结 语

利用ARM嵌入式系统可以由软件方便地实现分频法相位跟踪采样控制，而且有很好的实时相位跟踪性能和较宽频率跟踪范围；基于附加角度Δθ2的测量校正原理概念直观清晰，计算量极小且效果显著，对采样相位间隔进行校正后可以大大提高相位差测量的准确度；软硬件实现简单，功能扩展灵活。可广泛用于周期信号及谐波的频谱分析、数字相关解调、旋转机械动平衡、信号相位差、时间延迟、测距定位等及关联参数的精密测量。

[1] 程朋乐.面向装配的微小型零件视觉检测技术[J].电子测量与仪器学报,2013,27(2):151-155.

[2] 邬江,蒲书缙.利用互相关方法提取相位差技术[J].电子信息对抗技术,2016,31(4):22-25.

[3] 蔡炯.基于自相关函数包络检测的复合调制定距方法[J].计算机应用与软件,2015,32(9):123-126.

[4] Liang Y R,Duan H Z,Yeh H C,et al.Fundamental limits on the digital phase measurement method based on cross-correlation analysis[J].Review of Scientific Instruments,2012,83(9):S1-S9.

[5] 蒋婷,刘建平,张一闻.基于多麦克风阵列的枪声定位算法研究[J].计算机应用与软件,2012,29(12):229-231.

[6] 沈廷鳌,涂亚庆,刘翔宇,等.基于相关原理的非整周期信号相位差测量算法[J].振动与冲击,2014,33(21):171-182.

[7] 常宽,厉伟.基于全相位FFT的介质损耗因数测量算法的研究[J].工程与试验,2015,55(4):5-7.

[8] 刘玉周,赵斌.移相相关法计算相位差的研究[J].激光技术,2014,38(5):638-642.

[9] 解德英,谢品芳,付志红,等.电网工频信号非整周期采样误差分析[J].电子测量与仪器学报,2010,24(2):113-118.

[10] 张强,葛颖森,黄永升.基于DFT的数字相位计设计[J].自动化与仪器仪表,2015(2):33-35.

[11] 梁文军,杨世锡,魏义敏.基于FPGA的转子振动信号整周期等相位采样控制方法[J].机电工程,2011,28(2):148-152.

[12] 远坂俊昭.锁相环((PLL)电路设计与应用[M].何希才,译.北京:科学出版社.

[13] Yang Z,Chen Y.Research on measuring method of cone angle and auto-measuring system with high precision[C]//International Conference on Electronic Measurement & Instruments.IEEE,2011:287-290.

[14] 朱冰莲.数字信号处理[M].电子工业出版社,2011.

[15] 杨世锡,梁文军,于保华.振动信号多通道同步整周期数据采集卡设计[J].振动、测试与诊断,2013,33(1):23-28.

[16] 胡劲松,吴昭同,严拱标.提高旋转机械振动信号整周期采样精度的一种方法[J].浙江大学学报(工学版),2002,36(3):273-274.

PHASETRACKINGSAMPLINGCONTROLANDCORRECTIONFORCROSSCORRELATIONDIAMETERMEASUREMENT

Yang Zelin1He Yunxiang2He Li1

1(SchoolofElectricalandElectronicEngineering,ChongqingUniversityofTechnology,Chongqing400054,China)2(MeteringCenter,QijiangGearTransmissionCo.,Ltd,Chongqing401421,China)

In order to improve the accuracy of cross correlation diameter measurement，it is necessary to track the workpiece surface error signal by integer period and equal phase interval sampling. This paper introduces the principle of phase tracking sampling control by frequency division method. The influence of phase interval accuracy is discussed, and the concept of inherent error and random error is proposed, and the cause of the error is analysed. We introduce the additional angle measurement link to correct the sampling phase interval, and give the correction algorithm. Based on the ARM7 LPC2148 MCU embedded system, we introduce the implementation of phase tracking sampling control, calibration measurement and synchronization. Experimental tests show that the frequency division of the sampling control system will change and the phase tracking is good when the frequency fluctuation of the speed is greater than 1/1 000. At 3 000 r/min, the sampling phase interval error is controlled within 0.001 13 degrees. It is necessary to prove that the additional angle measurement and the sampling phase interval correction.

Diameter measurement Cross correlation Embedded system Phase tracking sampling Correction

TP271.81

A

10.3969/j.issn.1000-386x.2017.10.047

2016-11-30。重庆市教委科学技术研究项目(kj130833)。杨泽林，副教授，主研领域：动态测试，嵌入式系统及应用。何云祥，高工。何莉，副教授。