基于相似性填充和信任因子的协同过滤算法

王建芳 谷振鹏 刘冉东 刘永利

(河南理工大学计算机科学与技术学院 河南 焦作 454000)

基于相似性填充和信任因子的协同过滤算法

王建芳 谷振鹏 刘冉东 刘永利

(河南理工大学计算机科学与技术学院 河南 焦作 454000)

针对传统协同过滤算法中用户交叉评分项较少的情况，提出一种相似度与社交网络中信任因子结合的新方法。首先利用评分矩阵获取用户间相对缺失的评分项。其次通过概率矩阵分解技术进行降维获得近似评分矩阵，用以动态填充上述缺失项目评分，以填充后的用户评分计算用户间相似度。对于部分填充中存在误差的项目通过信任因子动态调整，获得更符合实际的相似度。在公开数据集MovieLens的实验结果显示，该方法较传统方法在推荐精度方面提升2.1%以上。

协同过滤 数据稀疏 相似性 填充 信任因子

0 引 言

互联网由Web1.0时代进入Web2.0时代，用户逐渐地由信息消费者扩展到信息生产者和消费者。随着用户参与信息生产，网络信息规模呈爆炸式增长。海量信息为信息检索提供了可能的同时导致了信息过载。为了缓和这种矛盾，帮助用户在海量数据中准确快速地找到其感兴趣的信息，推荐系统应运而生[1]。由于协同过滤能够处理电影、音乐和商品推荐等难以进行文本描述的项目，因而广泛应用于电子商务等行业[2]。虽然协同过滤取得显著优秀性能，但仍面临许多问题，例如实际应用中数据往往极度稀疏[3]。以电子商务为例，在电子商务系统中用户购买的商品通常不足网站商品总数的1%。用户只对极少数商品进行评分。传统的相似性计算方法仅使用共同评价项目，用户间具有隐式相似度，但由于没有共同评分项而无法计算其相似度。

国内外学者提出采用将降维技术来缓解推荐算法中的数据稀疏问题。Sarwar等[4]首先提出采用奇异值分解SVD(Singular Value Decomposition)，以矩阵分解角度实现降维，提取隐因子信息。Salakhutdinov等[5]提出概率矩阵分解PMF(Probabilistic Matrix Factorization)技术，给与SVD概率解释并加以正则项避免过拟合。台湾林智仁等[6]提出了支持向量机的研究对降维技术进行改进。降维技术在保留大部分数据信息的情况下减少数据维数，虽然取得一定成果，但不可避免的损失一部分有用信息。为了提高数据利用率，研究人员提出了改进相似性的计算方法[7-10]。Bobadilla等[11]提出利用均值填补缺失信息以充分挖掘用户特征信息。孙小华等[12]综合基于SVD的协同过滤算法和基于k近邻的协同过滤算法两者的优势，提出了Pear_Afrer_SVD算法。该算法先使用SVD技术对原始评分矩阵R进行分解。再通过分解矩阵逆向求近似评分矩阵。之后利用填充后的近似评分矩阵进行用户相似度计算，最后采用k近邻算法选择目标用户的邻居，并通过邻居做出推荐预测。

基于上述存在的问题，本文提出了一种基于用户和相似性填充的协同过滤算法CF-PFCF。该算法通过部分填充评分矩阵，用户所有的评价行为可以被充分挖掘，同时引入用户信任因子，能够有效地衡量每位用户评价信息的可信性和可靠性，避免用户的恶意评分行为，从而提高推荐精度。

1 相关工作

经过最近几年的研究，协同过滤模型已成为个性化推荐系统中应用最广泛的模型。典型的协同过滤可以分为基于内存的协同过滤和基于模型的协同过滤。基于内存的协同过滤考虑需要用户对项目的兴趣度，该信息通常以评分矩阵的形式表示。

矩阵中每一行ri表示用户i评价电影的集合，所有用户集合用U表示；每一列rj表示评价电影j的用户集合，所有电影集合用V表示。每一个元素ri,j表示用户i对电影j的评分。传统的协同过滤算法步骤为计算用户相似度、由相似度矩阵确定目标用户邻居集合，由邻居集合对目标用户预测评分三步。

郝立燕等[13]提出用SOFT_IMPUTE算法补全稀疏的评分矩阵结合相似度因子与k近邻算法做出推荐预测，通过补全的评分矩阵加以信任因子限制得到WCF-SOFT算法。基于填补的相似度计算方法不可避免地会使预测评分参与计算，影响原始用户特征信息。杨兴耀等[14]提出基于信任模型填充的协同过滤推荐模型CFTM，该方法通过分析日常人类行为习惯，利用评分矩阵采样建立信任模型对用户相似性进行填充。然而单纯信任因子无法充分挖掘用户特征信息。

基于模型的协同过滤则是通过对原始评分矩阵建模，迭代预测出评分矩阵中的缺失项，可有效解决数据稀疏问题和冷启动问题。PMF[5,15]是现代推荐系统中基于模型的协同过滤基础算法之一，核心思想是：假设用户与电影间的关系可以由少数几个因素的线性组合决定。用矩阵的角度来描述，评分矩阵R分解为两个低维矩阵的乘积 ，其中矩阵U为k×n阶矩阵，描述用户的k个属性，矩阵V为k×m阶矩阵，描述电影的k个属性。根据秩的性质，k不得大于矩阵R的秩。通过分解出的用户特征矩阵U和电影特征矩阵V，逆向可求得近似评分矩阵。

2 CF-PFCF算法思想

CF-PFCF算法是以用户历史评分数据为背景，遵循协同过滤的基础流程，首先对原始用户-评分矩阵利用PMF算法得到近似矩阵，该近似矩阵与均值相比更能反映用户行为，因此作为填充数据。其次针对性的填充用户间一方评价而另一方缺失评价的项目，计算填充相似度和共同评分相似度，以充分挖掘数据。然后计算用户信任因子，分别以用户共同评分下的相似度、用户的评分次数、用户评分和被评分项目均值之差来限制填充相似度。通过共同评分相似度和信任因子对填充相似度的共同限制，减弱相似性计算中的由填充带来的假设性，加权得到最终的调和相似度。以该调和相似度为基础由k-近邻算法得到用户邻居集。最后进行预测评分。

2.1 动态填充

填充稀疏矩阵的目的是更充分地利用已有评分信息计算用户之间的相似性，使得用户相似性计算更加准确。研究者已经提出许多填充评分矩阵缺失值的方法。其中最简单的填充方法以用户评分均值[16]、项目评分均值、用户评分中值、项目评分中值进行对用户并集中缺失值填充。该填充方法保证原始用户-评分矩阵的评分项参与运算，但用固定值填充导致被填充用户的特征被平均化。因此在一定程度上减弱了被填充用户的数据特征，致使计算相似度准确率不高，甚至降低准确率。

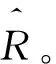
Va⊕b=Va∪b-Va∩b

(1)

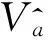
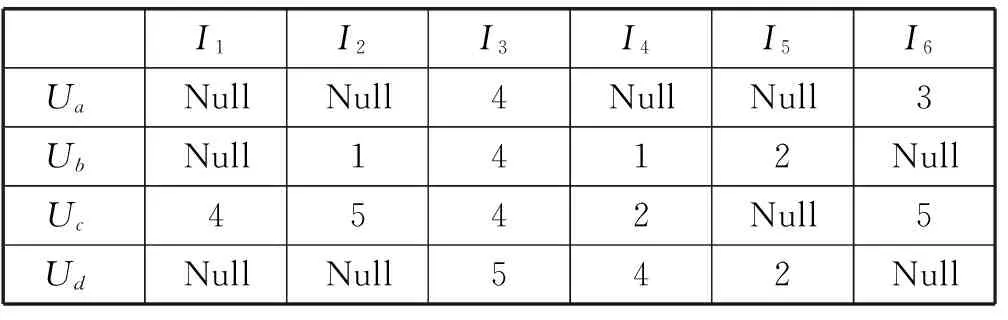
表1 评分矩阵

表1表示一个具有4个用户6个项目的评分矩阵，每行表示用户对所有项目的评分行为，Null代表该用户没有对项目进行评分操作。经式(1)填充方法和PMF方法可得填充逻辑表和近似评分矩阵如表2和表3所示。

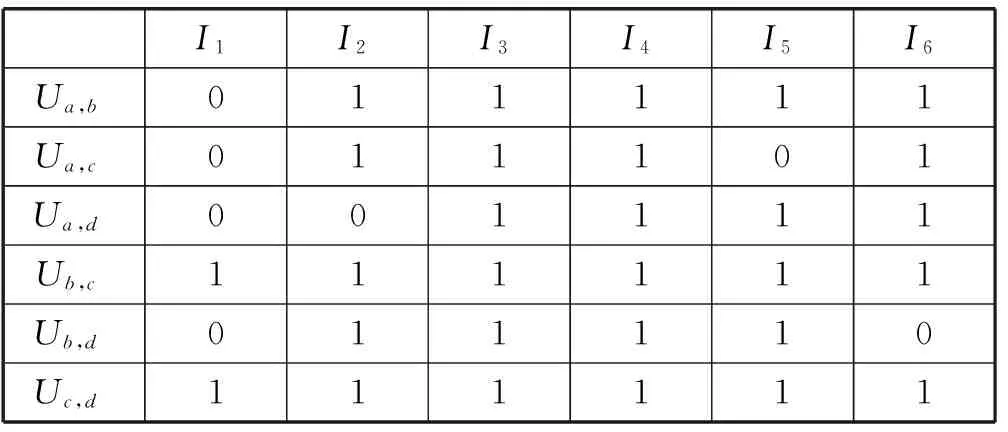
表2 填充逻辑矩阵

表3 近似评分矩阵

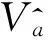
simfill_pearson(a,b)=

(2)

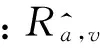
通过该填充算法，在保证充分利用原始评分矩阵用户特征信息的前提下避免过度填充，减弱填充算法中的假设性。

2.2 信任因子

虽然填充算法保证用户间评分信息充分参与计算，但由于原始评分矩阵过于稀疏，即使进行部分填充其相似度假设性依然较强，式(2)计算出的相似度没有考虑用户之间的实际关系。因此在进行预测评分时，应考虑到多种因素对相似性的影响，这些因素被称为信任因子[13]。

1) 基于传统皮尔逊相似度对其进行加权调整，通过式(1)对用户间共同评价项进行计算，得出传统皮尔逊相似度Simpearson，该相似度计算不带有任何填充项，可反映用户间真实关系。通过加权调整，可得调和的用户相似度，如式(3)：

Sim_adj=αSimfill_pearson+(1-α)Simpearson

(3)

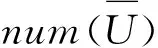
(4)

3) 实际中一些用户喜欢评高分，一些用户喜欢评低分，甚至存在恶意评分用户，单纯用户评价等级不能衡量用户的信任度，需要加以限制。因此引入评价偏差Du，如式(5)：

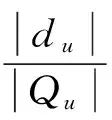
(5)

其中：Qu为用户u所评价过的电影集合，du为用户u评价偏差较小的电影集合。用户u对电影i的评价如果小于某个参考值则认为用户u对电影i的评价偏差较小，该用户的评价无异常。通常这个参考值取电影的评价均值。通过式(6)进行计算：

(6)

如果式(6)成立，则ru,i∈du。设置ε为0.5，实验显示ε越小，偏差要求越苛刻，取值过小会使用户丧失信任。

基于式(2)-式(6)对相似度进行加权调整，得到调和相似度，如式(7)：

Simtr=αSimfill_pearson+(1-α)Simpearson+w1Nu+w2Du

(7)

关于权重值的设定，可用机器学习算法、专家经验等，本文采用粒子群算法，不断交叉验证，最终获取一组较优的权重值例如(0.7,0.1,0.2)。通过调和相似度，运用k近邻算法对用户评分进行预测。

3 CF-PFCF算法描述

结合相似度部分填充和信任因子，提出CF-PFCF算法，具体步骤如下：

算法1CF-PFCF算法

输入：用户-评分矩阵R，待预测用户-评分项集合Rpre，邻居数k。

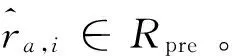
算法实现：

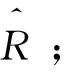
步骤2遍历原始评分矩阵R计算相似度矩阵Simfill_pearson和Simpearson；

repeat

步骤2.1获得用户ua和用户ub各自评价电影集合的交集Va∩b和并集Va∪b；

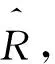
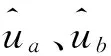
until遍历评分矩阵R；

步骤3遍历评分矩阵R计算信任因子；

repeat

步骤3.1获取用户ua和用户ub共同评分集合，并计算共同评分下的相似度；

步骤3.2统计每位用户评价电影总数得到用户评价数目集合num(u)；

步骤3.3统计每位用户评价过电影序号获得用户历史评价记录集合userv；

步骤3.4对每部电影求其平均评价值averv；

步骤3.5通过评分矩阵R得到对电影i评价过的用户集合UI；

until遍历评分矩阵R；

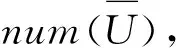
步骤5由averv和userv通过式(5)、式(6)计算用户评价偏差Du；

步骤6利用式(7)计算综合相似度Simtr；

步骤7通过对UI对应Simtr进行降序排序，取前k个用户作为用户ua的邻居集合Uneighbor；

步骤8预测用户-评分项集合Rpre；

repeat

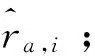
until遍历集合Rpre。

4 实验结果与分析

4.1 数据集与误差标准

本实验采用由美国明尼苏达大学GroupLens实验组创建并维护的Movielens-100K数据集包含943名用户对1 682部电影的100 000条评分，评分集为{1,2,3,4,5}，评分越大说明用户对电影的认可度越高。数据的稀疏度为100 000/(943×1 692) = 93.7%。为进一步验证本文算法的通用性，本文额外引用了Movielens-1M数据集，该数据集同样由GroupLens实验组提供。与Movielens-100K数据集相比，Movielens-1M数据集具有大的数据量，它包含了6 040个用户对3 706部电影的1 000 209个评分数据，数据的稀疏度为95.5%。实验将数据集划分为比例为8∶2的两个互不相交的训练集和测试集。

实验性能有许多评价标准，例如查全率、均方根误差、查准率等。本文采用平均绝对误差(MAE)作为度量标准。假设测试集中实际评分分别为{p1，p2，…，pn},算法预测的评分为{q1，q2，…，qn},则MAE定义为：

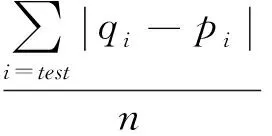
(8)

MAE值越小，说明算法可行性越强。

4.2 实验结果与性能比较

为了验证本文所使用的填充算法对传统协同过滤算法的改善作用，首先将皮尔逊、余弦、调整余弦相似度算法在Movielens-100K数据下进行对比测试。如图1所示。

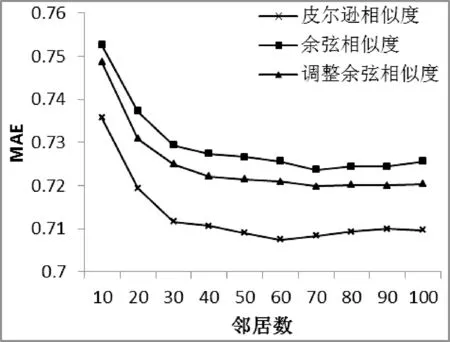
图1 传统相似度对比

实验结果显示：余弦相似度误差最大，皮尔逊相似度误差最小，三种相似度算法随着邻居数增多，误差逐渐减小并收敛。因此本文选择以皮尔逊相似度为基础进行实验。

以皮尔逊相似度为基础，对评分矩阵进行全PMF填充、部分PMF填充(本文所用填充方法)进行对比，如图2所示，其中全PMF填充方法为传统的填充算法，填充效果如表2所示。

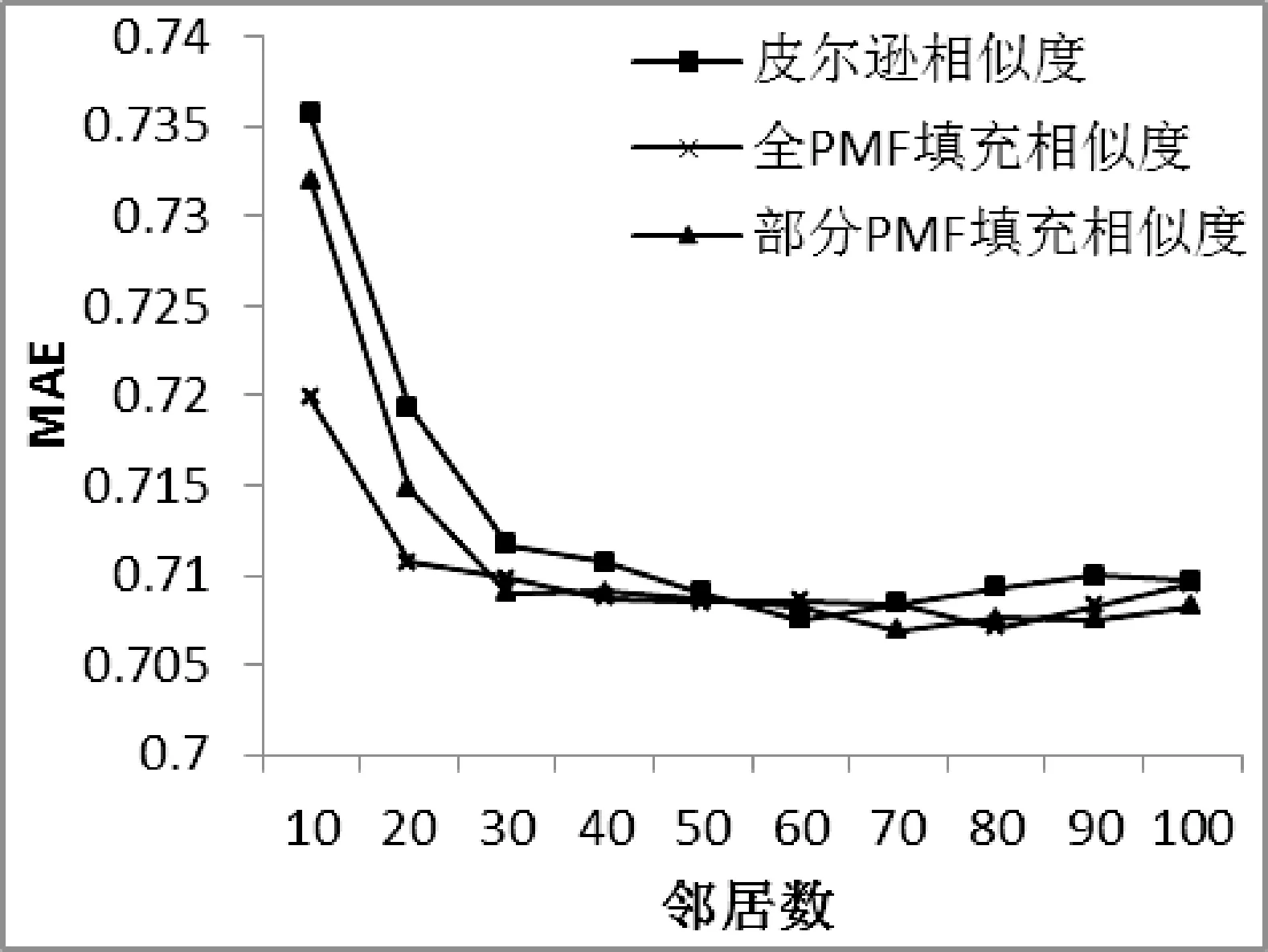
图2 改进相似度对比

基于皮尔逊相似度算法在邻居数少的情况下填充算法精度提高，部分PMF填充算法在邻居数为70的情况下精度达到最优。图1、图2表明单纯PMF填充相似度下精度提升依然不明显，为此加入原始皮尔逊相似度进行权重调整。

如图3所示，依上文式(3)进行相似度调和，实验结果显示，单纯填充相似度和单纯的皮尔逊相似度下的计算结果不理想，在基于全PMF填充算法下的权重调整中，权重因子α=0.8时结果最优。而在基于部分PMF填充算法下，权重因子α=0.7时结果最优，且优于全PMF填充算法的调和结果。

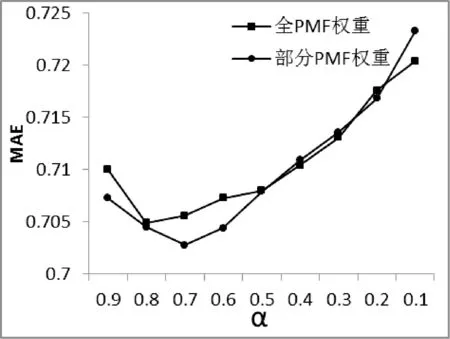
图3 填充权重对比

如图4所示，以部分PMF填充算法调和参数α=0.7为基础，结合式(7)，对参数w1和w2进行调参，其中x轴表示参数w1的变化，y轴表示w2的参数变化，z轴表示MAE，有图可得在参数w1=0.1和w2=0.2时，MAE达到较优。

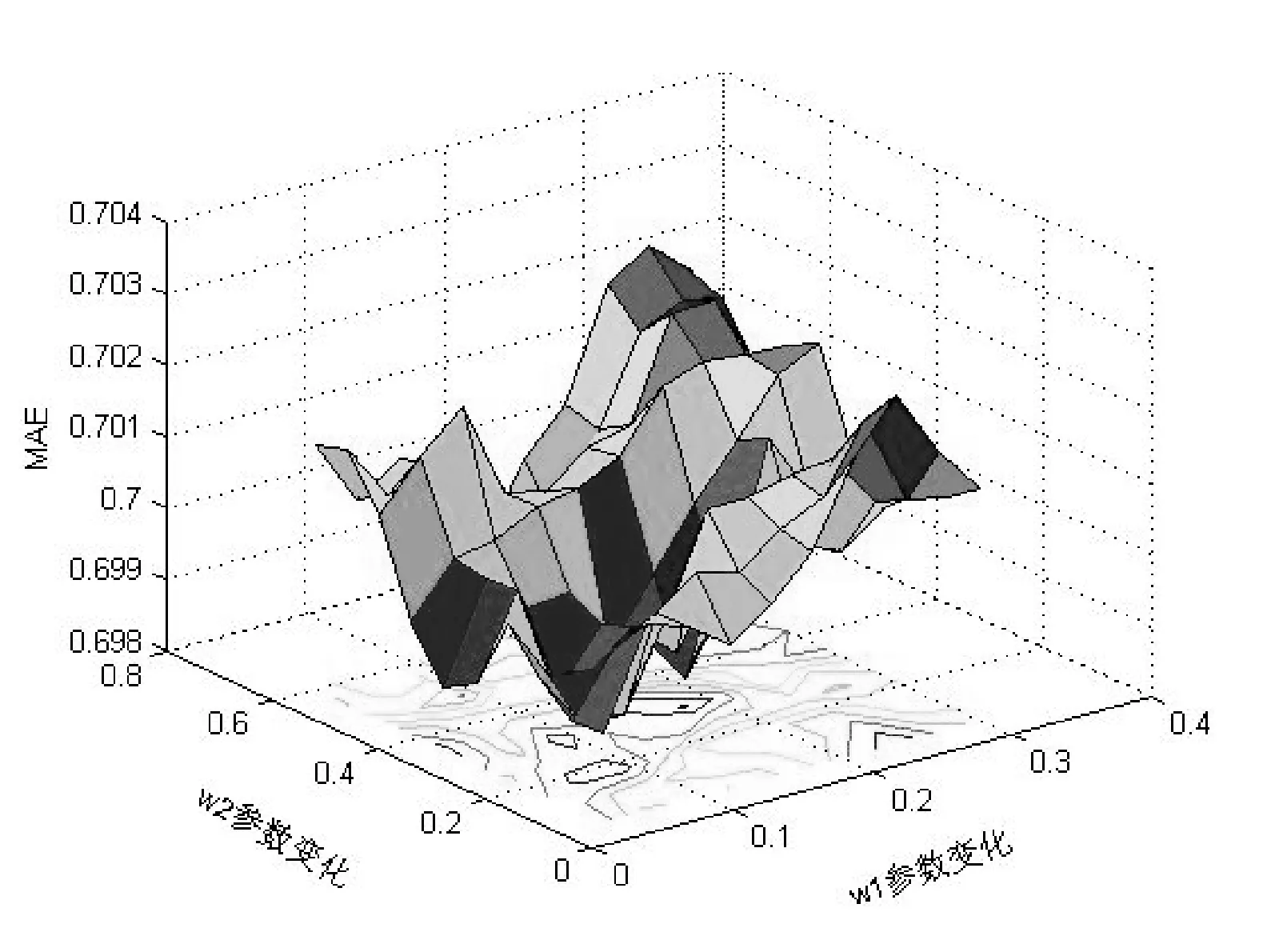
图4 调和权重对比

如图5所示在确定权重因子情况下对不同邻居数的实验结果进行对比，以皮尔逊相似度和部分填充PMF相似度预测误差作对比。实验显示在信任因子限制下，预测精度显著提升并在邻居数为40时达到最优。

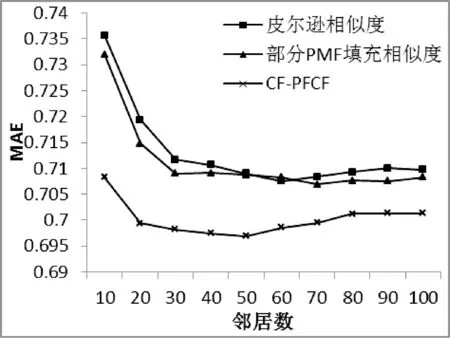
图5 CF-PFCF算法结果

将本文CF-PFCF算法与郝立燕等[13]提出的WCF-SOFT算法和杨兴耀等[14]提出的基于信任模型填充的协同过滤的CFTM算法做比较。在Movielens-100K数据集和Movielens-1M数据集下实验结果如图6、图7所示。通过计算可知本文方法较传统方法CFTM能提升3.6%推荐精度以上，较WCF-SOFT算法能提升2.1%推荐精度以上。

图6 基于Movielens-100K的性能比较

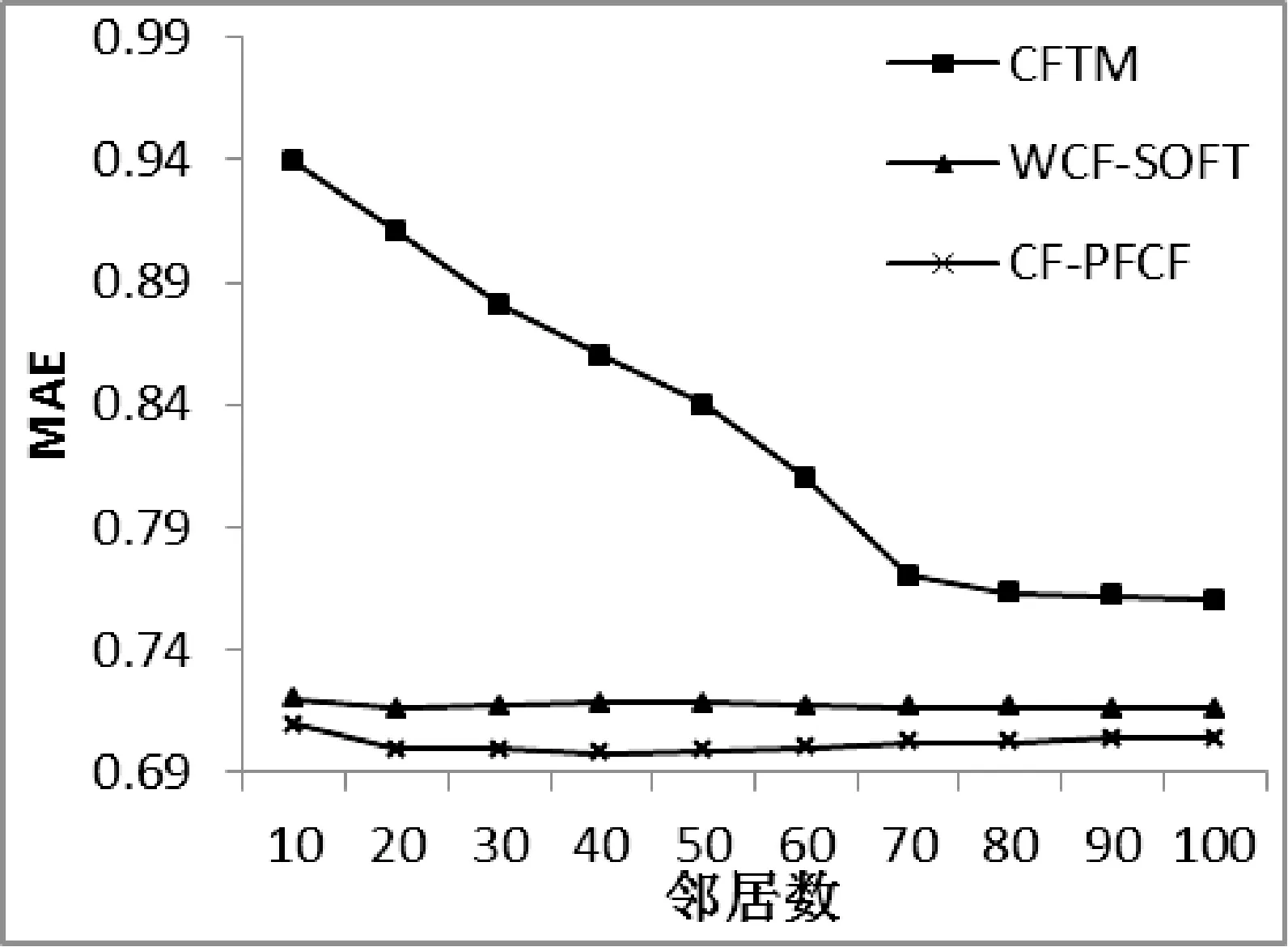
图7 基于Movielens-1M的性能比较

实验结果可以看出本文算法精度明显优于WCF-SOFT、CFTM算法。由于CFTM算法主要计算信任因子没有对相似度进行恰当改进，所以CFTM算法误差较大，在邻居数为90时达到最优，邻居数为100时误差上升。WCF-SOFT算法稳定性较强，本文算法对WCF-SOFT算法的填充部分进行改进，以部分填充代替全局填充降低填充评分的假设性成分，并加以共同评分相似度和信任因子共同限制。

5 结 语

本文对填充矩阵和信任因子做了研究，在高维稀疏的数据和基于用户的协同过滤算法的基础上提出部分相似性填充和信任因子概念。部分填充保证用户特征充分利用的前提下避免过度填充，解决了高维稀疏评分矩阵用户间共同评分稀少甚至缺失的问题，并对填充算法的假设性进行限制。尽管算法提高了整体精确度，但由于用户信任因子的影响，该算法随着邻居数增多精确度非单调下降。下一步需要研究如何增强算法稳定性，使误差随着邻居数增加单调递减并收敛。

[1] Aleksandra,Mirjana,Alexandros.Recommender systems in e-learning environments:a survey of the state-of-the-art and possible extensions[J].Artificial Intelligence Review,2015,44(4):1-34.

[2] Conforti R,Leoni M D,Rosa M L,et al.A recommendation system for predicting risks across multiple business process instances[J].Decision Support Systems,2015,69:1-19.

[3] Jing H,Liang A C,Lin S D,et al.A Transfer Probabilistic Collective Factorization Model to Handle Sparse Data in Collaborative Filtering[C]//IEEE International Conference on Data Mining.IEEE,2015:250-259.

[4] Sarwar B M,Karypis G,Konstan J,et al.Incremental SVD-Based Algorithms for Highly Scaleable Recommender Systems[C]//Conference on Computer and Information Technology,2002.

[5] Salakhutdinov B R,Mnih A.Probabilistic matrix factorization[C]//International Conference on Machine Learning,2012:880-887.

[6] Lee C,Lin C.Large-Scale Linear RankSVM[J].Neural Computation,2014,26(4):781-817.

[7] Lin H,Yang X,Wang W,et al.A Performance Weighted Collaborative Filtering algorithm for personalized radiology education[J].Journal of Biomedical Informatics,2014,51(1):107-113.

[8] Bokde D,Girase S.Matrix Factorization Model in Collaborative Filtering Algorithms:A Survey[J].Procedia Computer Science,2015,49(1):136-146.

[9] Algiriyage N,Jayasena S,Dias G.Web user profiling using hierarchical clustering with improved similarity measure[C]//Moratuwa Engineering Research Conference.IEEE,2015:295-300.

[10] Wu Z,Chen Y,Li T.Personalized recommendation based on the improved similarity and fuzzy clustering[C]//International Conference on Information Science,Electronics and Electrical Engineering.IEEE,2014:1353-1357.

[11] Bobadilla J,Serradilla F.A new collaborative filtering metric that improves the behavior of recommender systems[J].Knowledge-Based Systems,2010,23(6):520-528.

[12] 孙小华,陈洪,孔繁胜.在协同过滤中结合奇异值分解与最近邻方法[J].计算机应用研究,2006,23(9):206-208.

[13] 郝立燕,王靖.基于填充和相似性信任因子的协同过滤推荐算法[J].计算机应用,2013,33(3):834-837.

[14] 杨兴耀,于炯,吐尔根·依布拉音,等.基于信任模型填充的协同过滤推荐模型[J].计算机工程,2015,41(5):6-13.

[15] Yang W F,Wang M,Chen Z.Fast Probabilistic Matrix Factorization for recommender system[C]//IEEE International Conference on Mechatronics and Automation,2014:1889-1894.

[16] Mazumder R,Hastie T,Tibshirani R.Spectral Regularization Algorithms for Learning Large Incomplete Matrices[J].Journal of Machine Learning Research,2010,11(11):2287-2322.

ACOLLABORATIVEFILTERINGRECOMMENDATIONALGORITHMBASEDONSIMILARITYFILLINGANDTRUSTFACTOR

Wang Jianfang Gu Zhenpeng Liu Randong Liu Yongli

(SchoolofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo454000,Henan,China)

Since there are few users cross rating items in the traditional collaborative filtering algorithm, a new method is proposed to combine the similarity with the trust factor in the social network. First, the rating matrix is adopted to obtain the relative missing rating items between the users. Then, an approximate rating matrix is obtained by probabilistic matrix factorization method to selectively fill the missing rating matrix. Meanwhile, the trust factor is presented to adjust the error in process of calculate similarity. The results on the publicly available MovieLens datasets show that the proposed algorithm can improve the recommendation accuracy by above 2.1% on the classic algorithm.

Collaborative filtering Sparsity Similarity Filling Trust factor

TP391

A

10.3969/j.issn.1000-386x.2017.10.045

2016-12-22。国家自然科学基金项目(61202286)；河南省高等学校青年骨干教师资助项目(2015GGJS-068)；2015年度河南省高等学校重点科研项目(15A520074)。王建芳，副教授，主研领域：数据挖掘，人工智能。谷振鹏，硕士。刘冉东，硕士。刘永利，副教授。