混合最小二乘回归的稀疏子空间聚类算法

王 越 严 亮 张 强

(重庆理工大学计算机科学与工程系 重庆 400054)

混合最小二乘回归的稀疏子空间聚类算法

王 越 严 亮 张 强

(重庆理工大学计算机科学与工程系 重庆 400054)

稀疏子空间聚类的关键在于在求得真实反映数据集的相似度矩阵，然后将相似度矩阵代入谱聚类求解。相似度矩阵既要刻画数据集的子空间特性，同时也要反映出同一类数据点之间的两两相关程度，稀疏子空间聚类(SSC)专注于每一个数据表示系数的最大稀疏性，缺乏对数据集全局结构的描述;最小二乘回归(LSR)保证了同一类数据的结构相关性，但是不够稀疏。将最小二乘回归引入稀疏子空间聚类算法中，从而保证数据的相似度矩阵兼具稀疏性和分组效应。在运动分割和人脸聚类的实验中，将该算法和SSC、LSR算法对比，可以发现该算法在准确率上的优势。

稀疏子空间聚类 最小二乘回归 谱聚类 运动分割 人脸聚类

0 引 言

在聚类算法这个领域里，随着数据维度剧增，结构复杂化，很多聚类算法出现数据类之间差异无法判断，计算困难等问题。稀疏子空间聚类算法从2009年问世，如今在机器学习、计算机视觉、图像处理等众多领域有广泛用途。

在稀疏子空间聚类这个大家族中，涌现了许多卓越的算法，2009年Elhamifar等[1]提出稀疏子空间聚算法(SSC)用稀疏表示揭示了数据的本质特征，通过数据点的线性表示来划分不同的子空间，采用向量稀疏表示追求用最少的基或者字典原子来线性表示数据，过分追求数据的稀疏性，忽略了数据集的全局结构。2010年Liu等[2-3]提出的低秩子空间聚类(LRR)，选择通过相似度矩阵秩的最小化作为目标函数，秩是矩阵的稀疏度量(二维稀疏性)，虽然保证数据的全局结构，数据有噪声时稀疏差，不能准确反映子空间特性。2012年Lu等[4]提出最小二乘回归子空间聚类(LSR)，每一个数据点的线性表示时，通过采用最小二乘回归的方法来保证数据的全局结构，相比于LRR算法有较大进步。

本文通过考虑各种算法的优缺点，决定将最小二乘回归引入稀疏子空间聚类算法中，从而得到能反映数据的全局结构的同时又有足够稀疏性的相似的矩阵。在求解中引入最小二乘法的约束，从而避免过稀疏的缺点，同时添加数据集全局结构的因素，改善了稀疏子空间聚类算法不足，进而提高算法的鲁棒性和准确率。

1 相关工作

子空间聚类将高维数据表示成多个低维子空间的并，每一类对应一个子空间如图1。子空间聚类的求解方法有代数方法、迭代方法、统计学方法和基于谱聚类[5]的方法。前三种算法，在子空间的维数和个数未知的情况下，很难求解，并且奇异点和噪声对算法比较敏感。基于谱聚类的子空间分割方法，由于基于图谱理论，可以自动识别子空间维数和个数。

图1 三维空间可以看成是一个二维平面子空间和两个线性一维子空间

聚类融合[6]是利用不同的算法或同一算法寻找算法之间的切合点，以切合点为桥梁，将不同算法融合，来得到更高效稳定的聚类结果。本文研究重点是如何求解能真实逼近数据关系的相似度矩阵，针对两种不同算法考虑的侧重点不同，将他们融合进行取长补短，使得相似的矩阵更加准确。

2 原理及相关算法

2.1 稀疏子空间聚类

稀疏子空间聚类算法[7-10]，是运用子空间的基或者少量线性无关的向量来表示，让矩阵大部分系数都为0的子空间聚类算法。稀疏性的表现往往可以从系数矩阵的稀疏性看出。

设有n个D维的数据X={x1,x2,…,xn}，为了获得每个数据点的最稀疏的表示，经过凸松弛处理，稀疏最优化模型为：

(1)

输入：数据矩阵X，参数λ

初始化： Z=J=0,E=0,Y1=0,Y2=0,μ=10-6

maxu=1010,ρ=1.1,ε=10-8

While(‖X-XZ-E‖∞<ε&‖Z-J‖∞<ε)

Z=(I+XtX)-1(XtX-XtE+J+(XtY1-Y2)/μ)

Y1=Y1+μ(X-XZ-E)

Y2=Y2+μ(Z-J)

μ=min(ρμ,maxμ)

输出：系数矩阵Z

当子空间独立的时候，数据的系数矩阵成对角块结构，很好地将一个类区别开，每一个Zi代表一个子空间，Zi的个数代表子空间的个数，Zi的维度代表子空间数据点的个数。在得到数据点的系数后，由于每一个点所用的基不同，所以Zi,j≠Zj,i，为了保证对称性，令W=|Z|+|Z|T将系数矩阵W代入NJW谱聚类求得聚类结果。

SSC的缺点：

1) 在追求用尽可能少的基或者字典原子来表示数据时候，如果太过稀疏，同一类的数据点在相似度矩阵上的稀疏可能为0，这导致可能将同一类数据点划分到不同的类。

2) 如果同一类的数据两两之间相关性比较强，算法是随机选择子空间的基来表示，所以系数矩阵不能反映同一类数据两两之间相关性程度。

3) 不能高效地求解每一个数据点的l1-范数最小化问题，时间复杂度太高。

2.2 最小二乘回归(LSR)[4]

当子空间独立的时候，SSC、LRR[11]、MSR等算法都能保证相似度矩阵的块对角结构。稀疏子空间强调稀疏性，不仅是类间稀疏，同一类里面也同样稀疏，忽视了同一类数据相互间的结构关系，子空间分割中同一类里面的数据的相关性也是非常重要的，当数据充足的情况下，数据间往往具有较强的相关性。文献[4]当每一个数据被线性表示时，引入最小二乘法求解在整体上最佳逼近数据的表示系数，由于是NP问题，松弛为求解矩阵的Frobenius范数。

最小二乘回归优化模型：

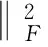
(2)

得到相似度矩阵W=|Z|+|Z|T，再将矩阵代入NJW谱聚类算法，求得聚类结果。

通过最小二乘法在求解相似度矩阵时，将每一数据的线性表示联合考虑，很好地保证数据的结构相关性，但是这样就会导致相比于SSC不够稀疏。

2.3 混合最小二乘的稀疏子空间聚类算法

目前考虑数据全局结构相关性最好的算法为最小二乘回归(LSR)算法，其充分利用数据之间的结构关系，在数据间的结构关系是用Frobenius范数的最小求解代替，可以保证数据间的结构关系，将Frobenius范数引入稀疏子空间聚类的。类间的稀疏性约束，是通过Z的l1-范数最小求解来达到的，为了平衡两者间的权重，将两者融合，选取适当的权重因子λ1。通过求解两者融合的目标函数，从而得到更逼近真实数据的相似度矩阵。于是本文提出将两种算法结合兼顾数据的稀疏性和分组性。

求相似度矩阵优化模型为：

(3)

算法

输入：n个D维的数据X={x1,x2,…,xn}。

1. 解决最小化问题得到Z=[z1,z2,…,zn]。

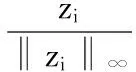
3. 得到相似度矩阵W=|Z|+|Z|T。

4. 对相似度矩阵W使用谱聚类。

输出：数据集的类分配。

3 实验内容

3.1 人工数据集进行实验

为了进一步详细了解数据的相似度矩阵，采用文献[12]的数据构造方法，构造方法其实就是两个自定义矩阵相乘，针对250个200维的数据集，数据由五个子空间构成，每个子空间为50×200的矩阵。实验结果如图2所示。

图2 三种算法的系数矩阵

实验结果表明：每一个方块代表一个子空间(代表一类)，图2(a)是用SSC算法求解的系数矩阵，属于一个子空间的相似度矩阵的系数不为0，其子空间内系数表示比较稀疏。图2(b)是用LSR算法求解的相似度系数矩阵，子空间系数比较均匀但不稀疏。图2(c)是用混合最小二乘回归的稀疏子空间聚类算法求解的系数矩阵，可以看到效果比较好。

为了检测本文的算法的性能，我们将算法分别在运动分割和人脸聚类进行实验，同时对比SSC和LSR算法。对于运动分割，采用Hopkins 155数据集，对于人脸聚类，采用Extended Yale B数据集。

实验中，采用聚类错误率来评价聚类算法的性能：

实验分别采用SSC、LRR、LSR、本文算法进行实验，并对比实验结果。

3.2 运动分割实验

运动分割[13]是指根据场景中的不同运动对一个包含多个运动物体的视频序列进行分割。传统的运动分割是根据多幅图像之间的相关信息进行运动估计，从而计算出运动场，再进行运动物体的分割。本文的运动分割是依据具有相同运动轨迹的点在同一个线性子空间上，通过子空间进行聚类。数据集为x为2F×N维，其中F为视频的帧数，N为二维轨迹的数目。这些二维轨迹通过跟踪算法提取。

Hopkins 155数据集包含两个或者三个运动的155个视频序列，其中两个运动物体的120个视频序列，三个运动物体的35个视频序列，由于单个固定运动的子空间维数不超过4，所以将数据点从2F维降到4n(n为聚类的数量)。如果直接进行使用会造成误差，降低准确率，通过降维，我们可以减少冗余信息造成的误差，从而提高聚类精度。数据进行降维实验，将实验结果可视化如图3所示。

图3 三种算法在car3数据上的可视化实验结果

不同算法在Hopkins 155上的实验结果如表1-表2所示。

表1 三种算法在Hopkins 155上的实验结果

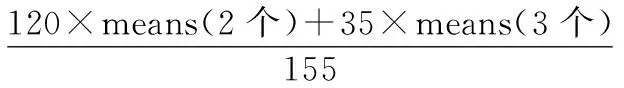
*Means(all)=

实验结果分析：本文采用不准确ALM算法来求解，因为求解需要反复迭代，所以算法运行时间较长，三种算法在运行时间是上相差不大。由于实验量比较大，本文选取均值和中值两个指标来评判实验的结果，从实验的数据上来看，当运动的个数增加的时候算法的错误率会有所增加，但是本文算法在均值和中值上面依旧错误率明显降低。

3.3 人脸聚类实验

人脸聚类[14]是将多个人在不同的光照，角度，表情下的一组图像集合进行聚类，依据同一个人的面部特征会处于同一个子空间理论，于是我们可以将Extended Yale B人脸数据集运用于子空间聚类。

Extended Yale B人脸数据集包含38个人，每一个人在不同光照、角度、表情下的人脸图像64张，将38人进行标号为1～38号。为了进行实验，将数据集分为1～10、11～20、21～30、31～38四组，每一组单独进行聚类实验，为了降低实验的计算复杂度，我们将192×168的图片抽样到48×42的图片，将一幅图片作为一个2 016维的数据点，来进行聚类。下面以两人不同光照和角度的20张图片为例，如图4所示。

图4 两个人的20张图的数据集

人脸实验的实验结果如表3所示。

表3 三种算法在Extended Yale B数据集上的结果

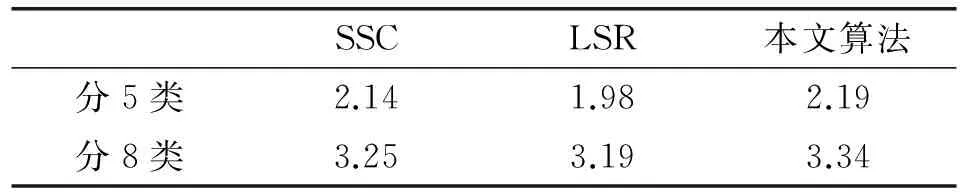
表4 三种算法在Extended Yale B上的运算时间/min

在实验中，对于四组数据集，我们对每一组进行单独实验，随机抽取数据进行聚类。由于聚类数低于5，准确率几乎100%，所以本文主要采用聚5类和聚8类，因为聚类数越多，各种算法之间的差异性就体现出来了。本文算法在人脸聚类实验中，算法运行时间并没有显著变化，但在准确率上高于目前流行的SSC、LSR算法。

4 结 语

本文将最小二乘回归融于稀疏子空间聚类中，从而得到兼具稀疏性和分组性的相似度矩阵，通过在Hopkins 155运动分割集和Extended Yale B中实验聚类效果优异。本文缺点是无法自动确定比重，其次算法都是针对线性子空间的，对于非线性子空间就不适用。这两点也是进一步研究的重点。

[1] Elhamifar E,Vidal R.Sparse subspace clustering[C]//Computer Vision and Pattern Recognition,2009.CVPR 2009.IEEE Conference on.IEEE,2009:2790-2797.

[2] Liu G,Lin Z,Yu Y.Robust Subspace Segmentation by Low-Rank Representation[C]//International Conference on Machine Learning.DBLP,2010:663-670.

[3] Liu G,Yan S.Latent Low-Rank Representation for subspace segmentation and feature extraction[C]//International Conference on Computer Vision.IEEE Computer Society,2011:1615-1622.

[4] Lu C Y,Min H,Zhao Z Q,et al.Robust and Efficient Subspace Segmentation via Least Squares Regression[M].Computer Vision-ECCV 2012.Springer Berlin Heidelberg,2012:347-360.

[5] Chen G,Lerman G.Spectral Curvature Clustering (SCC)[J].International Journal of Computer Vision,2009,81(3):317-330.

[6] 阳琳贇,王文渊.聚类融合方法综述[J].计算机应用研究,2005,22(12):8-10.

[7] 李小平,王卫卫,罗亮.图像分割的改进稀疏子空间聚类方法[J].系统工程与电子技术,2015,37(10):2418-2424.

[8] 付刚,吴观茂.迭代加权的稀疏子空间聚类[J].电脑知识与技术,2015,11(28):30-31.

[9] 李涛,王卫卫,翟栋.图像分割的加权稀疏子空间聚类方法[J].系统工程与电子技术,2014,36(3):580-585.

[10] 欧阳佩佩,赵志刚,刘桂峰.一种改进的稀疏子空间聚类算法[J].青岛大学学报(自然科学版),2014,27(3):44-48.

[11] 刘建华.基于隐空间的低秩稀疏子空间聚类[J].西北师范大学学报(自然科学版),2015(3):49-53.

[12] 刘紫涵,吴鹏海,吴艳兰.三种谱聚类算法及其应用研究[J].计算机应用研究,2017(4):1026-1031.

[13] 任永功.视频运动对象分割技术的研究[J].小型微型计算机系统,2004,6(3):1082-1085.

[14] 魏衍君,杨明莉.基于聚类建模的三维人脸识别技术研究[J].陕西科技大学学报(自然科学版),2012,30(2):77-81.

SPARSESUBSPACECLUSTERINGALGORITHMBASEDONLEASTSQUARESREGRESSION

Wang Yue Yan Liang Zhang Qiang

(CollegeofComputerScienceandEngineering,ChongqingUniversityofTechnology,Chongqing400054,China)

The key of sparse subspace clustering is to get the true reflection of the similarity matrix of data set. And then the similarity matrix is brought into the spectral clustering algorithm. Similarity matrix not only describes the data set, but also reflects the correlation of the within-cluster data. The sparse subspace clustering (SSC) focuses on the maximum sparsity of each data representation coefficient, lacks overall structure description of data sets. The least-squares regression (LSR) ensures the relevance structure of the within-cluster data, but is not sparse enough. We introduce the least-squares regression into sparse subspace clustering algorithms, so as to ensure the similarity matrix of the data is sparseness and grouping effect. Compared with SSC, LSR algorithm, our algorithm can produce more accurate results in the experiment.

Sparse subspace clustering Least-squares regression Spectral clustering Motion segmentation Face clustering

TP391.1

A

10.3969/j.issn.1000-386x.2017.10.042

2016-09-14。王越，教授，主研领域：数据库技术及应用，数据挖掘及应用。严亮，硕士生。张强，硕士生。