基于EEMD和改进多小波的故障诊断的研究

王海瑞 宋怡然 王 雪 李荣远

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

基于EEMD和改进多小波的故障诊断的研究

王海瑞 宋怡然 王 雪 李荣远

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

针对滚动轴承振动故障信号具有非线性和非平稳的特点以及多小波阈值函数的选取对去噪效果的影响，提出一种基于EEMD(总体经验模态分解)和改进多小波阈值结合的故障特征提取的方法。首先，使用EEMD方法对采集到的信号进行分解，根据峭度值以及能量值选取有效的IMF(基本模态)分量，再选取合适的多小波函数对选取的IMF分量进行去噪，最后利用频谱分析法对去噪后的IMF分量进行重构，从而识别出故障特征频率，并通过获取的频率判断故障类型。实验结果表明，此方法可行且取得了较好的效果。

EEMD 多小波 阈值 故障诊断 滚动轴承

0 引 言

目前，在滚动轴承的故障诊断中，主要以研究振动信号中所产生的故障特征进行故障诊断。一般来说，滚动轴承故障诊断技术分为4个过程：首先对选取的能反映出滚动轴承状态信息的信号进行预处理；接着对信号进行特征提取，选取能够反映其故障征兆的特征值；然后根据特征值选取与之相适合的处理方法对特征值进行分析，从而得出其故障的状态诊断与分析；最后按照结果做出相应的决策，及时对设备做出相应的处理。而提取故障特征的有效性决定了能否准确地判断故障类型。所以，判断滚动轴承故障的关键就是准确全面地提取故障特征信号中的信息。

EMD可用于非线性与非平稳信号处理，可是EMD分解本身存在模态混叠等不足，为减少模态混叠对实验结果带来的影响，Wu等提出了利用高斯白噪声的总体经验模态分解(EEMD)方法[1]。小波变换的多分辨分析使其在时频域都有较强的局部识别能力，多小波是对小波的继承与发展。多小波是由两个或两个以上的函数作为尺度函数生成的小波，不但具有小波的多分辨率分析，还具有对称性、正交性、高阶消失矩等特点[2]，但是对于小波来说，除了Haar小波外，其他小波基函数不能同时具有这些特点[3]。文献[4]将EEMD与改进小波阈值去噪结合，并使用算法优化阈值函数，在处理磁记忆信号时得到比较理想的效果；文献[5]对传统小波的阈值以及阈值函数进行改进，并应用在含噪声的心音信号中，不仅克服了传统阈值的不足，还较好地保留了信号的尖峰；文献[6]利用能量比自适应选择阈值，并应用到多小波阈值去噪上，结果比单小波方法具有更好的降噪效果，且更易于提取出早期故障信息；文献[7]将多小波消噪应用于抑制局部放电检测中的噪声干扰中，结果表明多小波不仅能够处理多种形态的局放信号，而且在抑制噪声同时，更好地保留局部放电信息。将基于上述内容，本文将EEMD和多小波方法结合起来，对滚动轴承进行故障特征信息的提取与诊断，为了进一步提高实验结果的准确性，提出一种改进阈值函数去噪的多小波去噪方法，并且与只使用EEMD的方法进行比较。实验结果得出的时域图与频谱图表明，此方法可行且取得了较好的效果。

1 EEMD方法

EMD对非平稳信号具有自适应分解的能力，但其本身存在模态混叠以及端点效应等问题。因此Huang等[8-9]在EMD的基础上提出了EEMD分解方法。即在原有信号中加入高斯白噪声并经过多次EMD分解，利用了白噪声的频率平均分布的统计特性，自适应地从滚动轴承振动信号中分离出高频调制信号，从而有效地抑制模态混叠问题。

EEMD算法分解过程具体如下：

(1) 对需要处理的信号x(t)加入随机高斯白噪声序列(一般白噪声标准差是原始信号标准差的0.1～0.4倍)。

(2) 对加入白噪声后信号进行EMD分解，得到K个IMF分量cj(t)及余项r(t)，j=1，2，…，K。

将上述步骤(1)、(2)重复N次，每次加入不同的白噪声序列。即：

(1)

式中，xi(t)为第i次加入白噪声后的信号，cij(t)为第i次加入高斯白噪声后分解所得第j个IMF，j=1，2，…，K。

(3) 计算分解后IMF的均值，把各个IMF的均值作为最终的结果。即：

(2)

(3)

式中，cj(t)为对原信号经过EEMD分解后所得第j个IMF分量。

2 多小波理论及阈值函数改进

2.1 多小波理论

多小波是在小波分析基础上的新发展。多小波是指由两个或两个以上的函数作为尺度函数生成的小波[10]。多小波具有小波的多分辨分析，所以与小波类似，多小波也有其尺度函数与多小波系数。其多尺度函数φ1(x),…,φm(x)与多小波函数φ1(x),…,φm(x)分别满足下列两尺度矩阵方程：

(4)

(5)

在式(4)、式(5)中，Gk、Hk分别为多小波r×r的低通和高通滤波器矩阵。

多小波的尺度系数与小波系数分别表示为Uj,k=(U1,j,k,…，Ui,j,k)T,Vj,k=(V1,j,k,…，Vi,j,k)T，则多小波的分解公式与重构公式如下：

(6)

(7)

(8)

常用的多小波包括GHM、CL及SA4[11]等，其中GHM多小波具有对称性、正交性、紧支撑性及二阶消失矩。多小波与小波的另一个区别为多小波在对信号进行分解和重构前后需要进行预、后处理。再根据实验效果，本文选择r=2的GHM多小波；预、后处理采用重复行预滤波方法。

2.2 多小波阈值函数的改进

多小波去噪过程如下图1所示。含噪声信号经过预处理之后进行多尺度小波分解，根据设定的阈值函数及数值处理噪声，然后完成多小波重构与后处理，从而获得去噪后的信号。

图1 多小波去噪流程图

其中阈值函数及数值的确定决定去噪效果，Donoho和Johnstone提出的软、硬阈值函数都具有一定的缺点[12]。为了减少传统阈值函数带来的不利影响，提高去噪信号的信噪比，结合软、硬阈值函数的优缺点，提出一种改进的多小波阈值函数，如下所示：

(9)

为了证明提出的改进阈值函数方法可以带来更好的效果，选择信噪比和均方根误差指标对降噪后的信号进行分析[13]，进而比较出三种阈值处理方法降噪效果优越性。其中当信噪比越大，均方根误差越小时，信号所含噪声成分越少，即说明此种方法的降噪效果越好。信噪比(SNR)和均方根误差(RMSE)具体表达式如下：

(10)

(11)

表1 给出了三种阈值函数处理方法得出的数据结果，由表所示，新阈值函数处理方法的两项指标都明显优于传统阈值处理方法。表明改进阈值后的多小波在信号去噪方面取得的效果更好。

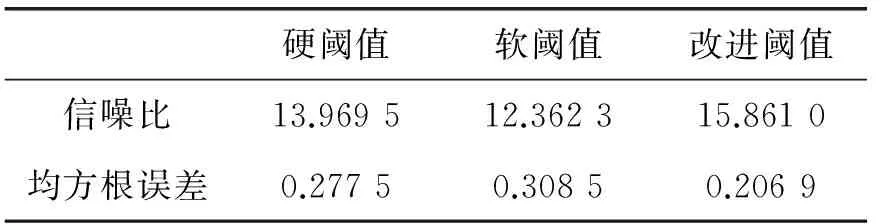
表1 三种阈值函数处理方法结果

3 实验分析

3.1 实验过程

峭度值反映了信号中冲击成分的大小[14]，当滚动轴承发生故障时信号会含有较多的冲击成分。其中信号中的冲击成分所占的比率越大，峭度值越大。当轴承出现故障时，由于接触部件的撞击会产生能量集中的周期性脉冲信号[15]。其中撞击越严重，信号中含有的能量越集中，数值也就越大。综合上述内容，选择峭度与能量作为筛选IMF分量的标准。峭度(K)公式与能量(E)公式分别为：

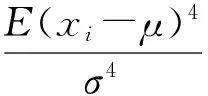
(12)

(13)

在式(12)、式(13)中，σ代表信号的均方差，μ代表信号的均值。

以内圈故障信号为例，表2为内圈故障信号经EEMD分解后的前六个IMF分量的峭度与能量，峭度值从大到小排列分别为：IMF1、IMF2、IMF3、IMF5、IMF4、IMF6；能量值从大到小排列分别为：IMF1、IMF2、IMF3、IMF4、IMF5、IMF6。综合两个指标，选择IMF1、IMF2、IMF3分别进行多小波阈值去噪后进行重构。

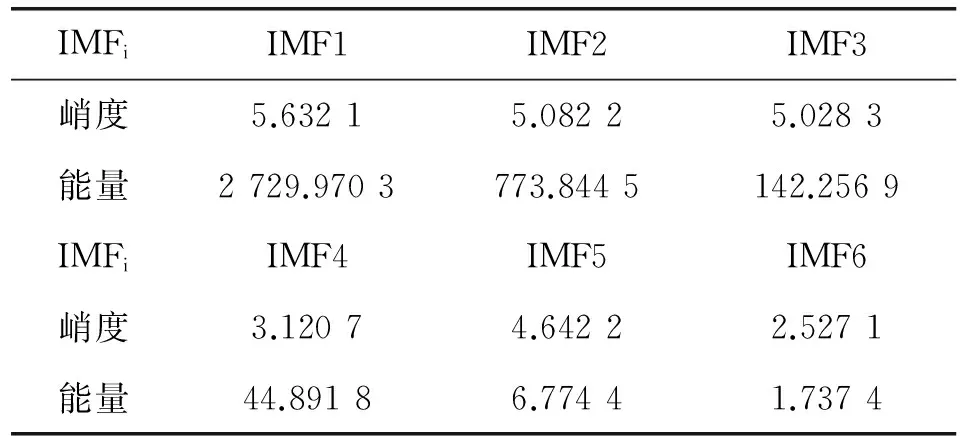
表2 各IMF分量峭度值与能量值

通过上述分析，利用EEMD与多小波的滚动轴承故障诊断可以分为以下几个步骤：

(1) 应用EEMD方法对待处理信号进行分解，分解出多个IMF分量，根据峭度准则以及能量值的大小按从大到小排列，并综合选取前三个IMF分量。

(2) 选用改进的阈值函数作为多小波降噪中的阈值处理函数。

(3) 对选取出的IMF分量分别采样多小波阈值方法进行降噪处理并重构。

(4) 为了验证方法的有效性，使用频谱分析法对重构信号进行分析与处理，从而判断出故障类型。

3.2 实验信号分析

本文利用美国凯斯西储大学振动实验室提供的数据进行实验，此振动信号的采样频率为12 KHz。三种故障频率如表3所示，分别为内圈(162 Hz)，外圈(107 Hz)，滚动体(141 Hz)。

表3 三种故障频率值

此实验室给出的数据故障信号都含有噪声，为了突出本文方法在处理噪声干扰方面的优势，图2、图4、图6分别为三种不同故障信号未经过处理和使用本文处理后的时域图。从对比图可以直观地看出，在原信号的时域图(a)中很难分辨出滚动轴承故障明显的冲击特征，但是经过EEMD分解和多小波去噪处理后，时域图(b)中的冲击特征得到了明显的变化。

根据时域图的对比效果可以看出本文提出方法在去噪效果上表现较好。为了进一步证明方法结合的优越性，图3、图5、图7分别给出了内圈、外圈以及滚动体故障信号重构IMF分量的频谱图。其中(a)图为没有进行去噪处理的频谱图，(b)图为经过改进多小波阈值去噪处理后频谱图。从两者的对比图可以看出，虽然进行EEMD分解后筛选出的前三个IMF分量重构后保留了信号中的有效信息，可以分析出故障频率。而由于EEMD分解后的IMF分量是按从高频到低频的顺序排列的，在高频成分的IMF分量中常含大量的随机噪声，所以重构后的信号在没有进行去噪处理后依旧保留了噪声影响。从图3(a)、5(a)、7(a)中可以看出有明显的噪声频率干扰，这样会影响最终的故障类型的判断。而图3(b)、5(b)、7(b)的频谱不仅分析出故障频率，还有效的去除了噪声的干扰，效果明显。综合分析图2-图7的时域图与频谱图，说明本文的方法可以应用到滚动轴承的故障诊断中，并且可以取得好的实验效果。

图2 内圈故障处理对比时域图

图3 内圈故障处理对比频谱图

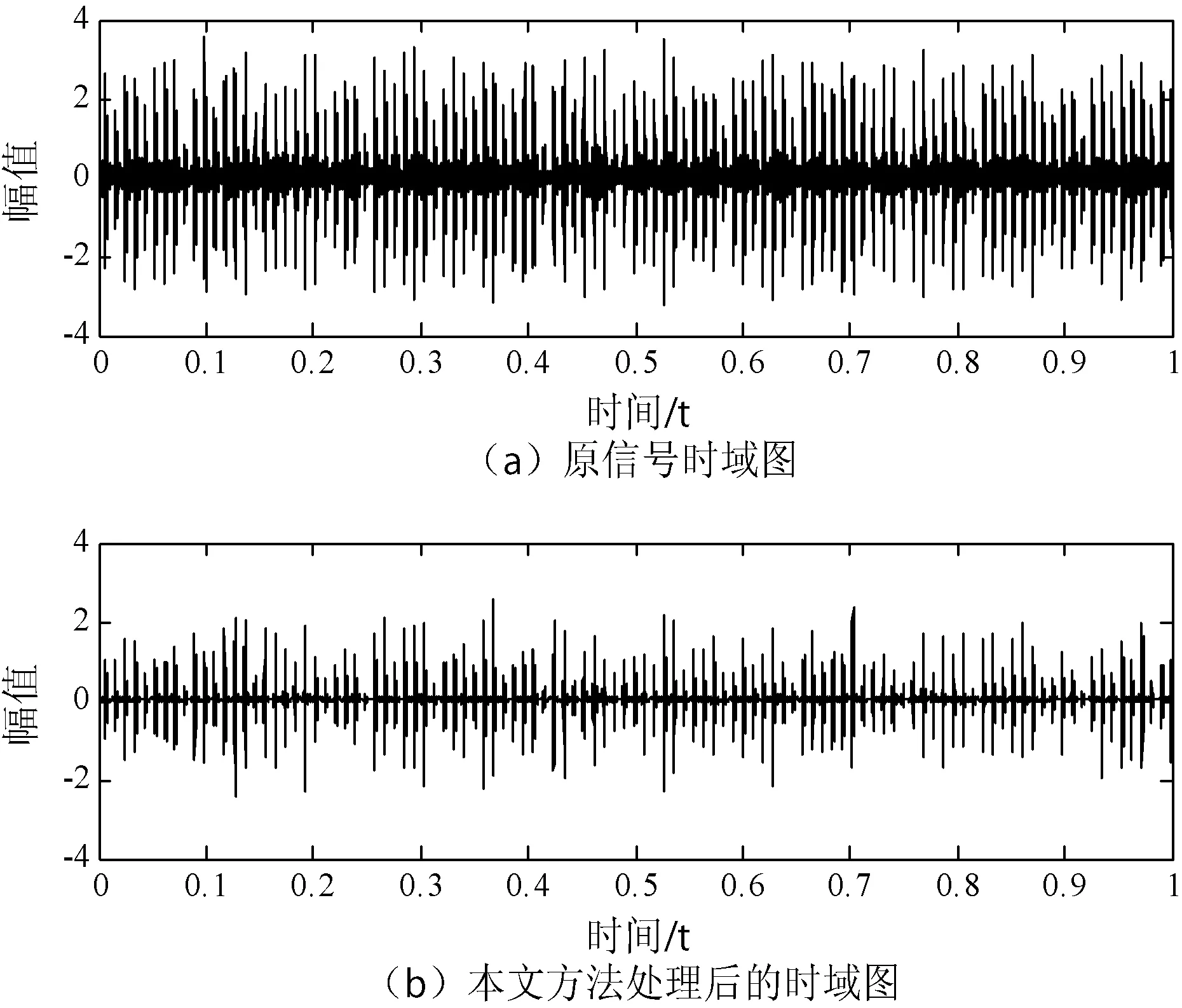
图4 外圈故障处理对比时域图

图5 外圈故障处理对比频谱图

图6 滚动体故障处理对比时域图

图7 滚动体故障处理对比频谱图

4 结 语

针对滚动轴承的故障分析，本文提出基于EEMD与多小波改进阈值的故障提取方法，首先应用EEMD对原信号进行分解，自适应的分解成多个IMF分量，根据峭度值与能量值综合选取含有故障信息最丰富的前几个IMF分量，但重构后的IMF分量中依然含有随机噪声，不能直接进行故障诊断；多小波作为一个新兴的去噪方法，其对称性、正交性、高阶消失矩等特点使其在去噪方面取得了较好的效果，已广泛应用在电力信号及图像处理中，但是在滚动轴承中的应用还比较少。在此基础上又提出了一种改进的阈值去噪方法，使多小波的去噪效果得到了进一步加强。相比于单一的使用EEMD方法进行故障提取，本文方法在故障提取方面效果更好。

[1] Wu Z, Huang N E.A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proc. R. Soc. Lond. A, 2004,460：1597-1611.

[2] Goodman T N T, Lee S L. Wavelets of Multiplicity r[J].Transactions of the American Mathematical Society, 1994,342(1):307-324.

[3] 卢娜.基于多小波的水电机组振动特征提取及故障诊断方法研究[D].武汉：武汉大学，2014.

[4] 张雪英，谢飞，乔铁柱，等.基于EEMD与改进小波阈值的磁记忆信号降噪研究[J].太原理工大学学报，2015，46(5)：592-596.

[5] Wang Y, Wang H, Liu L, et al. An Improved Wavelet Threshold Shrinkage Algorithm for Noise Reduction of Heart Sounds[C]//International Conference on Electrical and Control Engineering. IEEE, 2010:5018-5021.

[6] 张建宇，李文斌，张随征，等.多小波自适应阈值降噪在故障诊断中的应用[J].北京工业大学学报，2013，39(2)：166-172.

[7] 钱勇，黄成军，陈陈，等.多小波消噪算法在局部放电检测中的应用[J].中国电机工程学报，2007，27(6):89-95.

[8] Huang N E, Shen Z, Long S R, et al. The Empirical mode of decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc Royal Society，1988，454:903-995.

[9] Wu Zhaohua, Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]．Advances in Adaptive Data Analysis，2009，1(1)：1-4.

[10] 程正兴，杨守志，张玲玲.多小波理论的发展与研究[J].工程数学学报，2001，18(5)：1-16.

[11] Khadem S E, Rezaee M. Development of vibration signature analysis using multiwavelet systems[J].Journal of Sound & Vibration, 2003,261(4):613-633.

[12] 曹京京，胡辽林，赵瑞.一种改进小波阈值函数的光纤光栅传感信号去噪方法[J].传感技术学报，2015，28(4)：521-525.

[13] 刘志刚, 黄慧汇. 基于不同预处理方法的多小波暂态信号去噪[J]. 电子学报, 2004, 32(6):1054-1056.

[14] 吴小涛，杨锰，袁晓辉，等.基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J].振动与冲击，2015，34(2)：38-44.

[15] 胡爱军，马万里，唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]．中国电机工程学报，2012，32(11)：106-111.

THERESEARCHOFFAULTDIAGNOSISBASEDONEEMDANDIMPROVEDMULTI-WAVELET

Wang Hairui Song Yiran Wang Xue Li Rongyuan

(FacultyofInformationEngineeringandAutomation，KunmingUniversityofScienceandTechnology，Kunming650500，Yunnan,China)

For rolling vibration fault signal with nonlinear and non-stationary characteristics and the selection of multi-wavelet threshold de-noising function affects the results, a fault feature extracted method based on EEMD and multi-wavelet improved threshold is proposed. First, we adopted EEMD method to decompose the collected signal, and then picked kurtosis and energy as the standard to select a valid IMF component, and then selected the appropriate function of the multi-wavelet to make the IMF component de-noised. Finally, the IMF component is reconstructed by spectral analysis method to identify the fault characteristic frequency, and the fault type is determined by the frequency acquisition. Experimental results show that this method is feasible and has achieved good results.

EEMD Multi-wavelet Threshold Fault diagnosis Rolling

TP302.1

A

10.3969/j.issn.1000-386x.2017.10.026

2016-12-28。王海瑞，教授，主研领域：计算机应用，故障诊断。宋怡然，硕士生。王雪，硕士生。李荣远，硕士生。