塑性铰法分析现浇楼板钢筋混凝土框架结构抗震性能
孙威,黄炎生
塑性铰法分析现浇楼板钢筋混凝土框架结构抗震性能
孙威,黄炎生
(华南理工大学土木与交通学院,广东广州,510640)
为提高建模和分析效率,提出通过修改梁端塑性铰属性来模拟楼板效应的方法。塑性铰法采用杆系单元建模,由梁与楼板的共同受力特性推导出梁端转角和弯矩承载力的关系,并以塑性铰属性的方式赋予整体杆系分析模型。应用该方法对1个典型的2层钢筋混凝土框架结构进行抗震性能分析,将计算结果与直接建立楼板的分析模型计算结果进行比较。研究结果表明:本文提出的塑性铰法能够有效的对楼板的作用效应进行模拟。
钢筋混凝土框架结构;抗震性能;楼板效应;塑性铰属性
进行钢筋混凝土框架结构的抗震性能分析是保证结构在地震作用下安全可靠的重要依据,分析结果的准确性直接关系到结构的安全性能。国内外学者早在20世纪七八十年代就已经发现现浇楼板对框架梁端的抗弯能力具有不可忽视的增强作用,并进行了大量的研究。王素裹等[1−4]使用有限元软件ABAQUS研究了现浇楼板对RC框架结构破坏形式的影响,并得出了采用建议的现浇楼板有效翼缘宽度考虑楼板效应的等代方法。林旭川等[5]对考虑楼板效应的RC框架结构进行了震害仿真分析。PANTAZOPOULOU等[6−11]通过实验以及数值分析证明了框架梁因楼板的参与,在一定程度上改变了其抗弯刚度和承载力。此外,刘源等[12−16]从“强柱弱梁”的角度研究现浇楼板的作用。上述研究表明:忽略楼板的作用效应,仅采用梁柱杆件模型来分析结构的抗震性能,将导致分析结果产生较大误差。目前主流的结构分析软件多数采用杆系有限元模型,同时通过板壳单元来考虑楼板效应,由于板壳单元本身复杂性以及与杆单元位移协调等问题,分析结果并不理想。采用实体单元分析可以保证较高的精度,但实体单元法同时存在建模复杂,计算耗时等诸多缺陷。如何有效的在抗震性能分析中考虑楼板作用是本文的研究重点。本文作者通过研究梁端处梁和楼板的共同受力特性,推导出考虑楼板效应时梁端转角和弯矩承载力曲线,将该曲线以塑性铰属性的方式赋予整体杆系分析模型,用以计算结构整体的抗震性能。以2层典型钢筋混凝土框架结构为例,进行Pushover抗震性能分析,结果表明,该方法能够有效地模拟出地震作用下楼板的作用效应,求得的Pushover曲线与实体单元建模分析所得的Pushover曲线吻合良好。
1 框架结构梁端力学性能
通过梁端的力学表现来模拟楼板的作用效应,首先需要了解钢筋混凝土框架结构梁端本身的力学性能,以及考虑楼板作用效应后梁端力学性能发生的相应变化规律。
1.1 梁端截面弯矩承载力计算
图1所示为梁端截面示意图。不考虑楼板效应,当梁端上部拉筋为2排放置时(图1),梁端弯矩承载力可由下式计算求得:

框架梁因楼板的协同作用,在一定程度上改变了梁端的弯矩承载力。由于板筋的参与,框架结构梁端参与承受弯矩作用的受拉钢筋面积增加,此时,考虑梁端和楼板作用的截面弯矩承载力计算公式如下:

钢筋应力和混凝土应力符号统一表述为,拉应力为正,压应力为负。
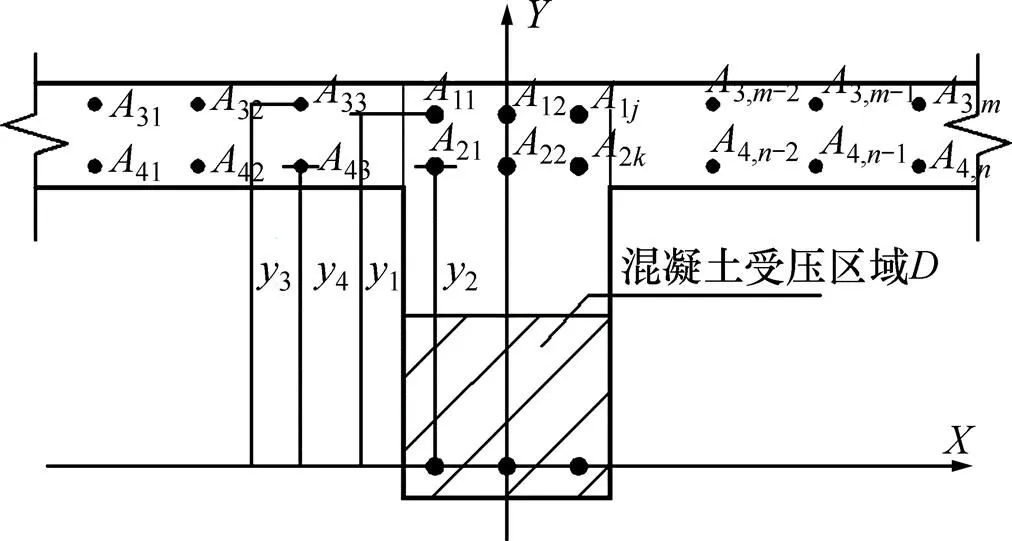
图1 梁端截面示意图
1.2 梁端塑性区域转角计算
钢筋混凝土框架结构梁端承受弯矩作用时,随着荷载增加,钢筋屈服之后,截面的承载能力提高幅度有限,而其相应的曲率增大迅速,此时,该截面相当于一个能转动的塑性铰。塑性区域转角示意图如图2所示。由图2可知:梁端转角=1+2(其中:1为梁端塑性区域自身转角;2为框架梁弹性区域相对于塑性区域的转角)。同时在塑性区域尺寸详图中,3对应于1,4对应于2,由简单的几何关系可推导,3=1,4=2。由于梁端转动角度一般较小,因此,可近似认为tantan1tan2tan3tan4。再由塑性区域的几何尺寸,以及塑性区域内钢筋的拉、压应变,梁端转角的计算公式可表示为
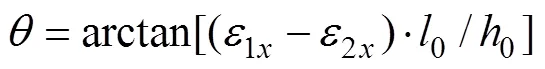
(a) 塑性区域尺寸详图;(b) 梁端转动简图
图2 塑性区域转角示意图
Fig. 2 Schematic diagram of rotation angle in plastic zone
2 塑性铰法的计算原理及步骤
2.1 塑性铰法计算模型说明
塑性铰法计算的核心是准确的模拟出考虑楼板效应时梁端的力学性能。选用合适的模型进行分析是达到该要求的必要条件。钢筋混凝土框架结构中,由于所处位置的不同,框架梁可分为2种:边梁和中梁(后文未加说明时,边梁和中梁均表示考虑楼板效应后的梁模型)。图3所示为塑性铰法计算模型。独立梁、边梁和中梁的分析模型均取梁跨度的一半进行建模,同时固结柱的底端作为边界条件(图3)。图3中为柱纵向间距,为柱横向间距。独立梁模型为基础计算模型,与杆件单元模型相对应。边梁和中梁模型均为实体单元分析模型。
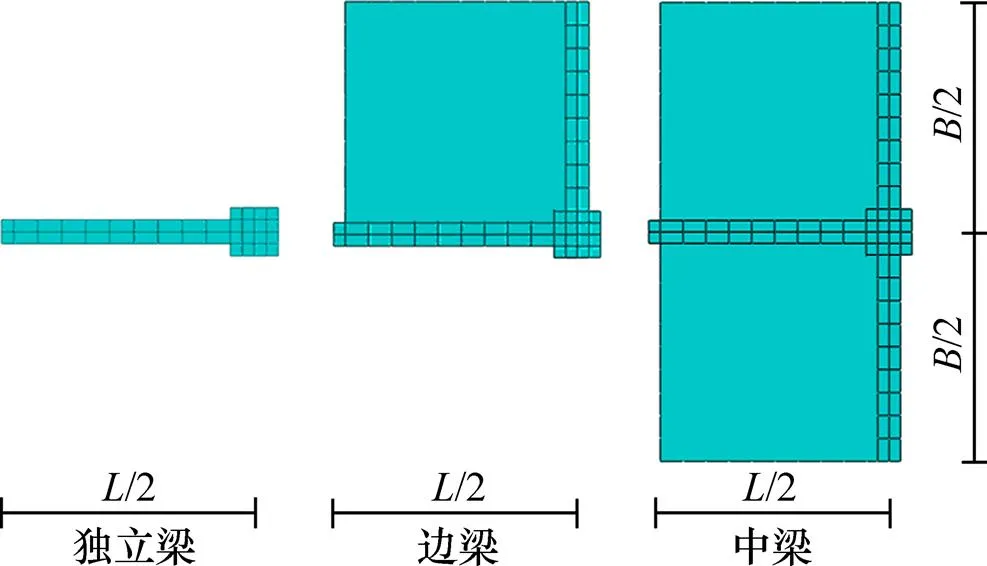
图3 塑性铰法计算模型
2.2 梁端塑性铰曲线说明
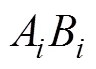

1—独立梁;2—边梁;3—中梁。
2.3 塑性铰法计算原理
塑性铰法的计算原理为:将实际配筋情况下实体建模的中梁(或边梁)模型所求得的梁端转角和弯矩承载力曲线,采用塑性铰属性方式赋予到整体杆系分析模型中对应的杆件单元,以达到考虑楼板效应的目的。为了清楚描述塑性铰法的计算原理,首先介绍下杆系模型中杆件单元截面特性以及其塑性铰默认计算原则。一般有限元分析软件中的杆件单元,其截面通常为规则矩形,在杆件端部定义的塑性铰,其属性曲线中的1点和1′点(图4中独立梁塑性铰初始转角对应点)将通过已定义的杆件截面属性(截面尺寸和配筋情况等)自动计算生成,1点和1′点(图4中独立梁塑性铰破坏转角对应点)的弯矩值默认取为其对应1点和1′点的1.1倍。如何以规则截面形式的独立梁杆件等效模拟出中梁(或边梁)模型计算得到的梁端塑性铰的力学性能,是塑性铰法计算需解决的首要问题。据 图4,该问题可简化表述为在杆件单元中,如何将按实际配筋的梁端塑性铰属性曲线111转变为实体模型计算得到的边梁(或中梁)塑性铰属性曲线222(或333)。
本文提出梁端有效拉筋面积修正系数、梁端弯曲刚度增大系数和塑性铰强化系数的概念,用以阐述杆件单元中塑性铰属性的转换问题。
1) 梁端有效拉筋面积修正系数。实际配筋情况下,梁端的计算截面如图5所示。
由图5可看出:板筋对于梁端弯矩的贡献,离梁越近的板筋贡献度越大;反之,板筋离梁距离达到一定程度后,对梁端弯矩的贡献很小。由于板筋的参与,使得独立梁梁端弯矩承载力由原来的1(对应于图4中的数值),变化为2(或3)。通过研究发现,在杆件单元的截面属性中,通过修正梁端的拉筋面积,可达到修正塑性铰初始转角时刻梁端弯矩承载力的 目的。
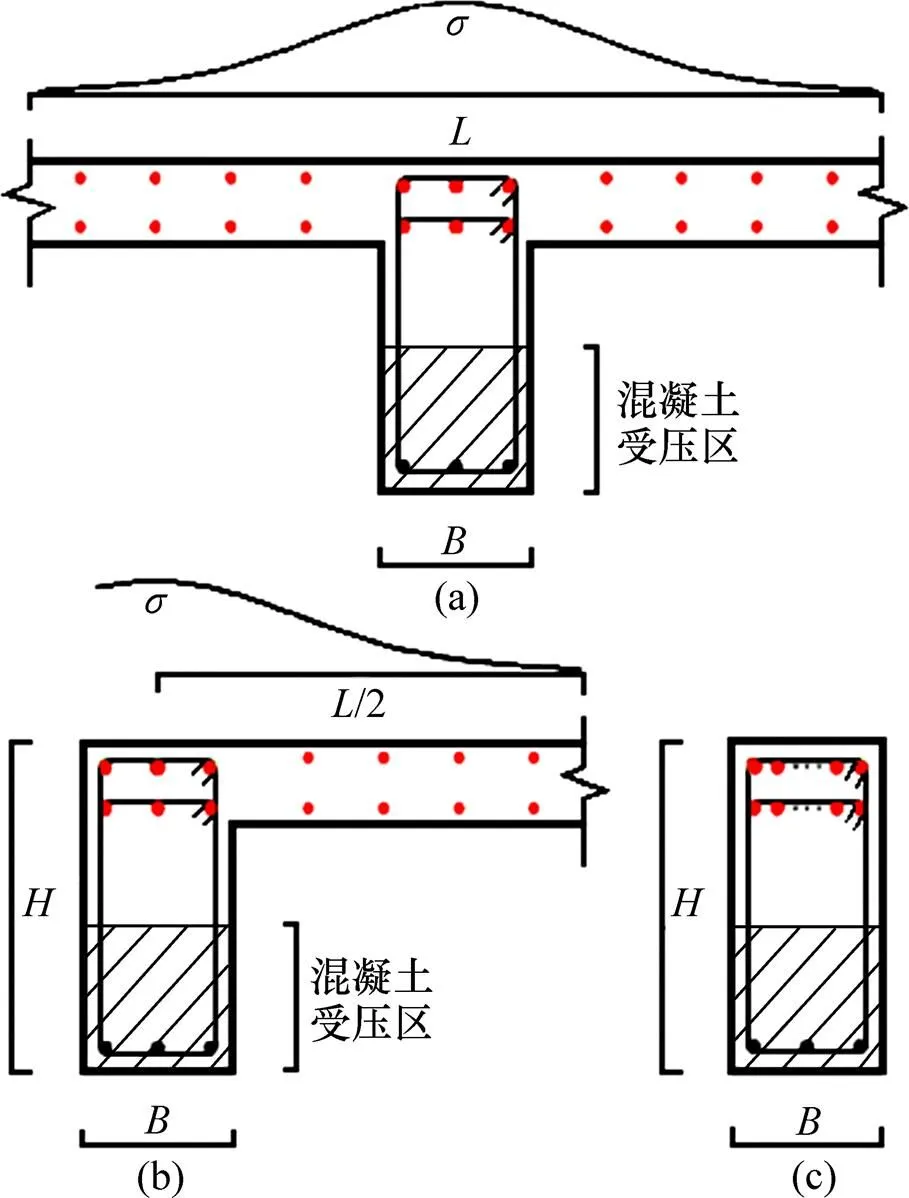
(a) 中梁梁端计算截面;(b) 边梁梁端计算截面;(c) 规则杆件单元所需定义的截面
2) 梁端弯曲刚度增大系数。从图4可知:边梁(或中梁)在梁端塑性铰产生前的弹性阶段,梁端弯曲刚度比较于独立梁,均有一定程度的增大。仅对梁端拉筋面积进行修正,并不能真正将1段曲线转换为2段曲线(或3段曲线),还需对梁端的弯曲刚度进行调整。
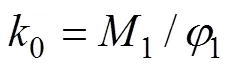
3) 塑性铰强化系数。塑性铰产生后,进入塑性铰强化阶段,梁端拉筋屈服,应力达到限值。靠近梁端的板筋也逐步达到应力限值,对应于图4中AB区段。从图4可看出:边梁(或中梁)在塑性铰强化区段的曲线22(或曲线33)与独立梁在塑性铰强化区段曲线11的斜率并不相同。
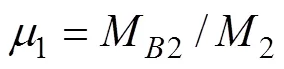
综上,通过有效拉筋面积修正系数、梁端弯曲刚度增大系数和塑性铰强化系数这3个系数对杆件单元梁端拉筋面积的修正以及截面属性的调整,可有效模拟出中梁(或边梁)模型计算求得的塑性铰属性曲线。
2.4 塑性铰法计算步骤
塑性铰法计算结构抗震性能的步骤可分为5 部分。
1) ABAQUS有限元分析软件中分别建立独立梁、边梁和中梁计算模型。
2) 在远离柱的梁端分别施加正负位移荷载,应用式(1)和式(2)分别计算出各荷载步梁端截面弯矩承载力,并汇总得到梁端转角和梁端弯矩承载力的关系 曲线。

4) 由2.3节内容计算边梁和中梁塑性铰属性的修正系数:梁端有效拉筋面积修正系数、梁端弯曲刚度增大系数和塑性铰强化系数。
5) 按实际配筋形式建立杆系模型,通过第4步的塑性铰修正系数分别对边梁和中梁梁端配筋和塑性铰属性进行修正,采用修正后的杆系模型计算结构Pushover抗震能力曲线。
3 整体模型法的计算步骤
整体模型法作为验算塑性铰法的一种方法,在ABAQUS有限元分析软件中,采用实体单元模拟混凝土,线单元模拟钢筋,并采用embed技术模拟混凝土与钢筋之间的连接作用。按照实际配筋情况建立模型,并赋予相应的荷载与边界条件。记结构顶点侧向位移为,底层柱总水平剪力为,加载水平地震作用后,从计算结果中提取各荷载步下顶点侧向位移和底层柱总水平剪力的数据,绘成曲线,即为整体模型法求得的结构抗震能力曲线。
4 算例分析
通过一个具体算例来介绍塑性铰法如何求解钢筋混凝土框架结构的抗震性能。算例模型为2层标准钢筋混凝土框架模型,如图6所示。楼层层高为3 m,跨度为4 m。梁、柱纵筋强度为400 MPa,楼板板筋强度为300 MPa。梁、柱纵筋直径为16 mm,板筋直径为8 mm,板筋间距为100 mm。梁截面尺寸(长×宽)为200 mm×400 mm,柱截面尺寸(长×宽)为400 mm×400 mm。梁、柱截面配筋如图7所示,箍筋直径为8 mm,间距为100 mm。梁、柱保护层厚度为20 mm,楼板保护层厚度为15 mm。梁上结构自重等效线荷载=10 kN/m。采用Pushover方法分析其抗震性能。
4.1 塑性铰法
在ABUQUS有限元软件中建立图8所示独立梁、边梁和中梁计算模型,并在远离柱的梁端分别施加正、负位移荷载。以图8所示施加的荷载为例,计算得到混凝土应力分布云图和钢筋应力分布云图。
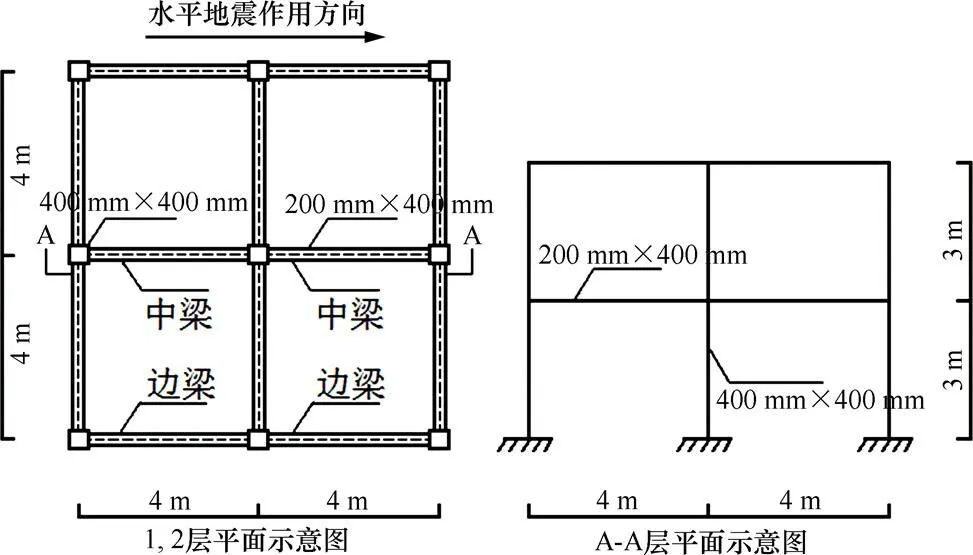
图6 钢筋混凝土框架结构示意图

图7 梁柱配筋示意图
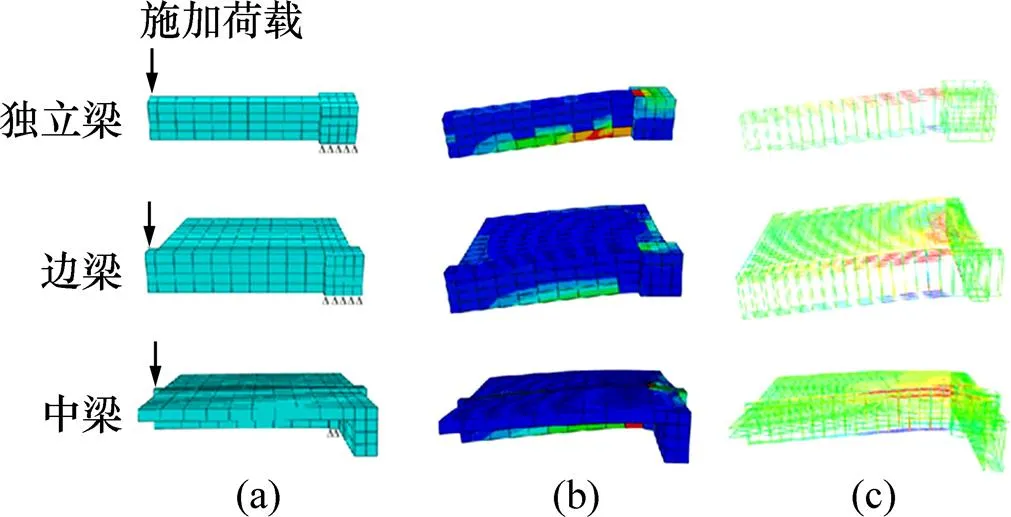
(a) 模型;(b) 混凝土应力云图;(c) 钢筋应力云图
提取各荷载步对应的钢筋应力,采用式(1)和 (2)求取独立梁、边梁和中梁梁端截面在各荷载步下的弯矩。同时通过式(3)计算得到各荷载步下梁端塑性区域转角。将求取的弯矩和转角数据绘于图13中。其中,曲线1、曲线2和曲线3分别表示独立梁,边梁和中梁的梁端转角与弯矩关系曲线。由独立梁梁端转角和弯矩关系曲线,可得塑性铰初始转角为1=0.4°,1′=−0.28°,塑性铰初始时刻独立梁梁端弯矩1=159.7 kN∙m,1′=−89.9 kN∙m,塑性铰破坏时刻转角2=3.012 7°,2′=−3.012 8°。
由图13中数据,通过2.3节塑性铰属性修正系数的相关计算,可得边梁和中梁的梁端有效拉筋面积修正系数、梁端弯曲刚度增大系数和塑性铰强化系数,结果如表1所示。

1—θ1/2塑性铰转角;2—θ1塑性铰转角;3—θ2塑性铰转角。
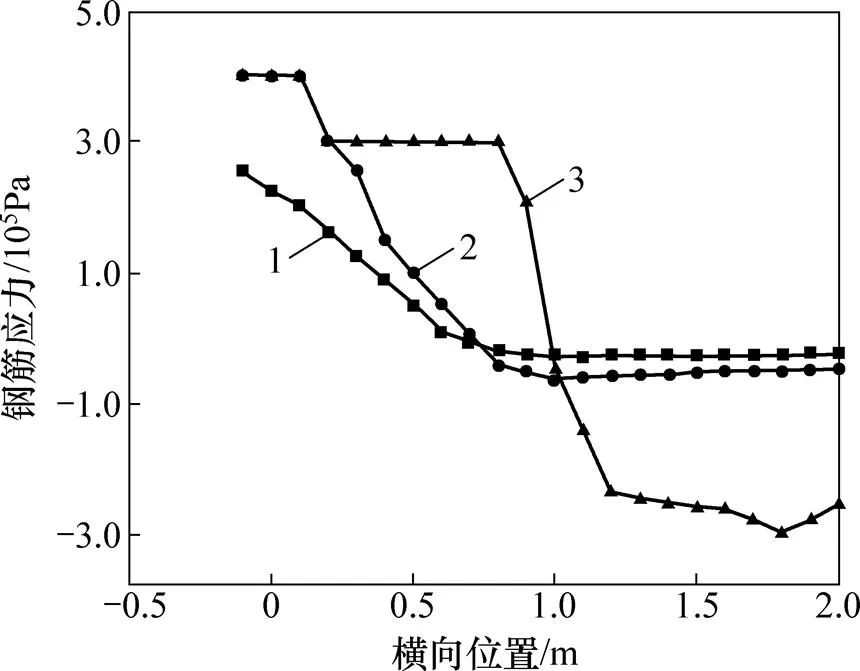
1—θ1/2塑性铰转角;2—θ1塑性铰转角;3—θ2塑性铰转角。
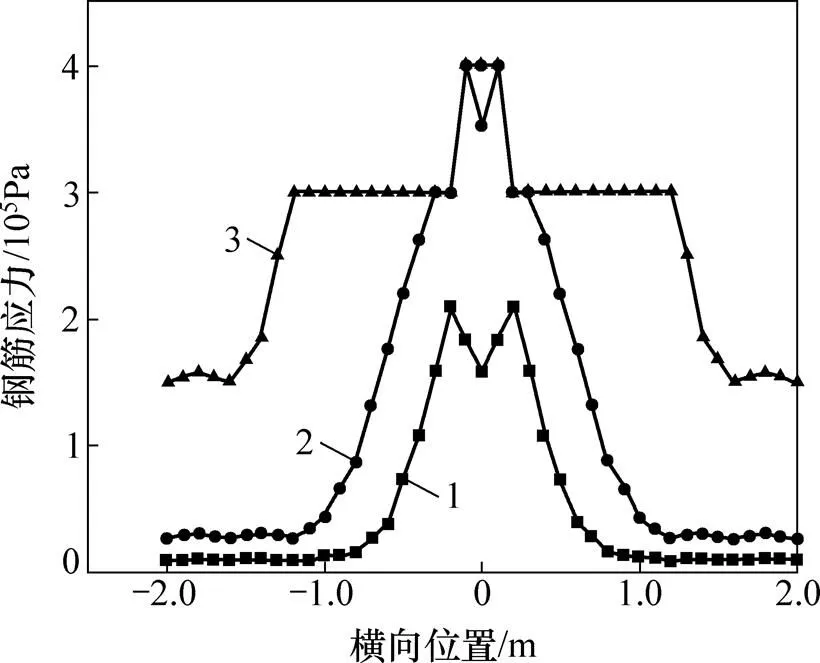
1—θ1/2塑性铰转角;2—θ1塑性铰转角;3—θ2塑性铰转角。

1—θ1/2塑性铰转角;2—θ1塑性铰转角;3—θ2塑性铰转角。
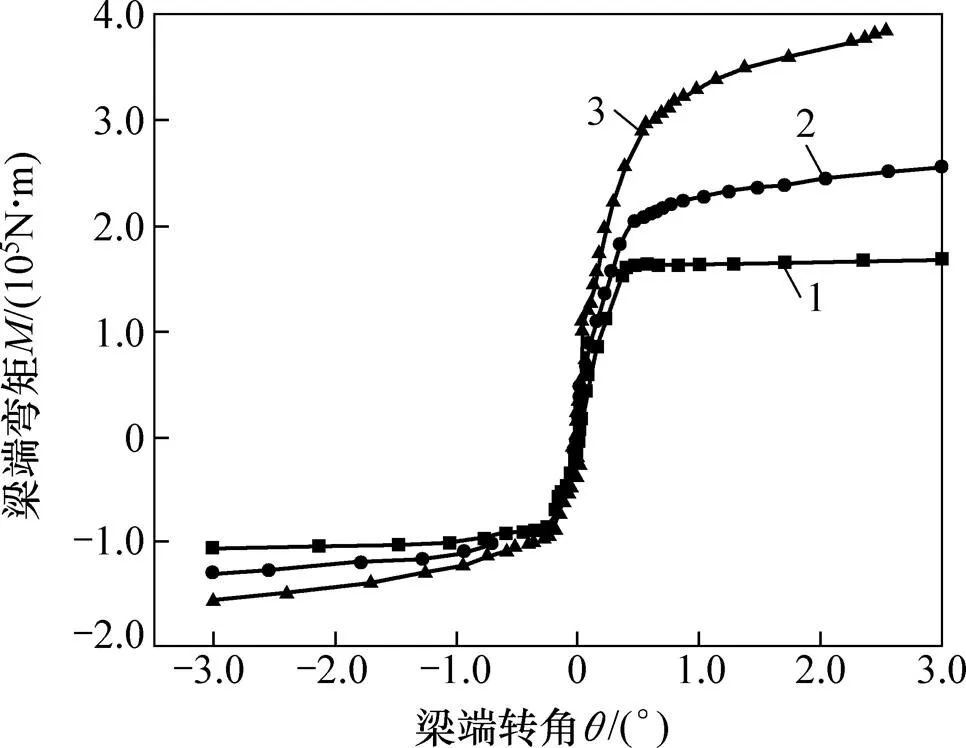
1—独立梁;2—考虑楼板的边梁;3—考虑楼板的中梁。
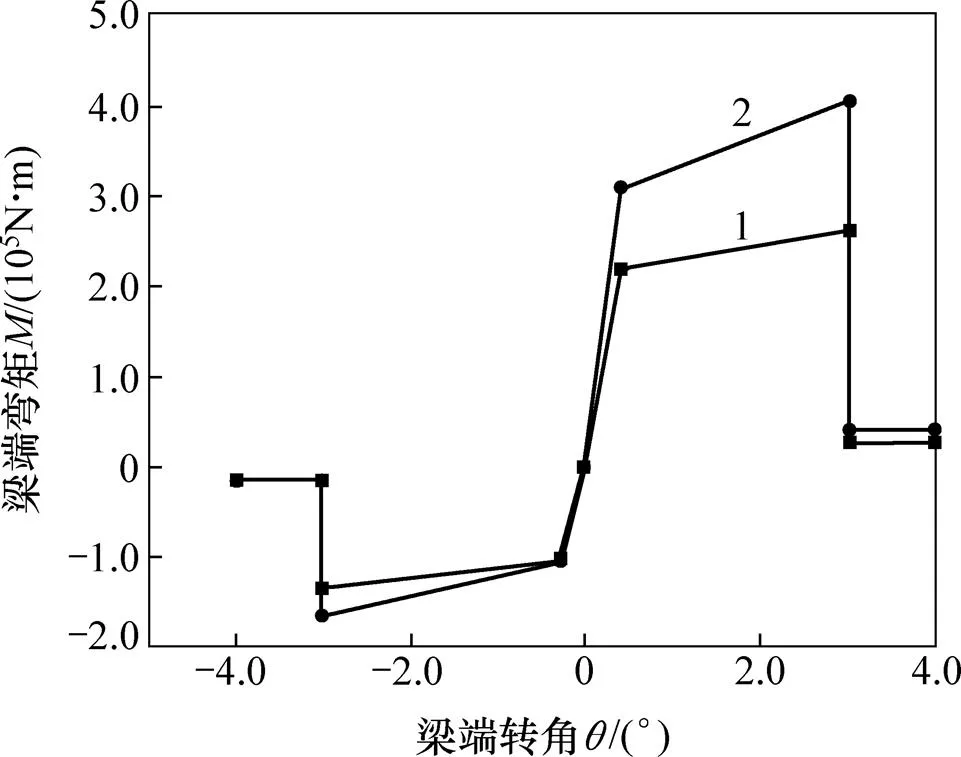
1—考虑楼板的边梁;2—考虑楼板的中梁。
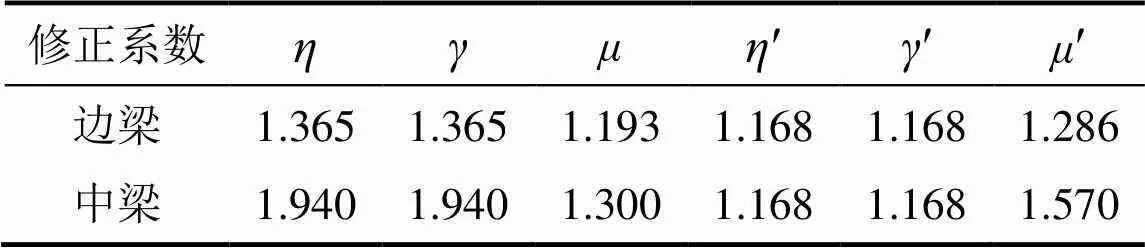
表1 塑性铰属性修正系数
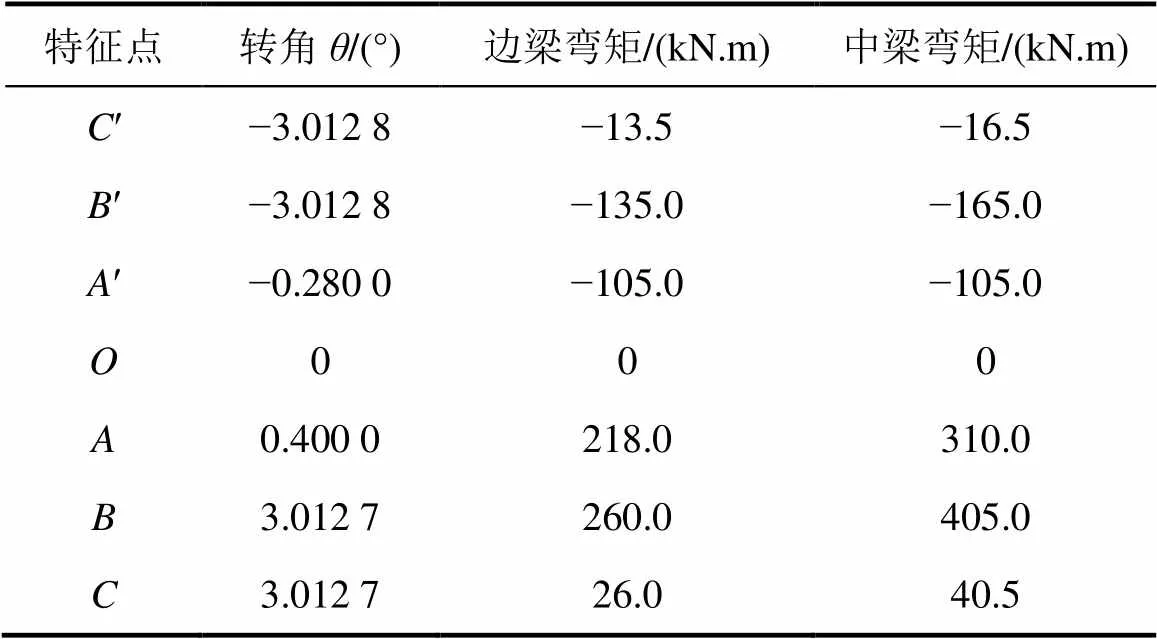
表2 塑性铰转角与弯矩
在SAP2000杆系模型中,按照梁端有效拉筋面积修正系数调整杆系单元的拉筋面积,同时按照梁端弯矩刚度增大系数和塑性铰强化系数来调整杆系单元的塑性铰属性。将调整后的杆系模型进行Pushover抗震性能分析,10 s左右便能求得计算结果。Sap2000杆系模型的塑性铰示意图如图15所示,对应的Pushover曲线如图16所示。
4.2 整体模型法
在ABAQUS有限元软件中采用整体模型法建立模型,地震作用以及边界条件均与4.1节相同,进行抗震性能分析,分析耗时30 min,得到楼板竖向位移云图如图17所示。从图17可以看到楼板在梁端变形中的协同作用情况。

图15 Sap2000有限元模型塑性铰示意图
将塑性铰法和整体模型法计算得到的Pushover曲线汇总于图18中,同时在图18中绘出未考虑楼板效应的整体模型法Pushover曲线作为对比曲线。由图18可知:塑性铰法计算得到的Pushover曲线和整体模型法计算得到的Pushover曲线吻合良好,而未考虑楼板效应的Pushover曲线与考虑楼板效应的Pushover曲线之间存在较大差异。
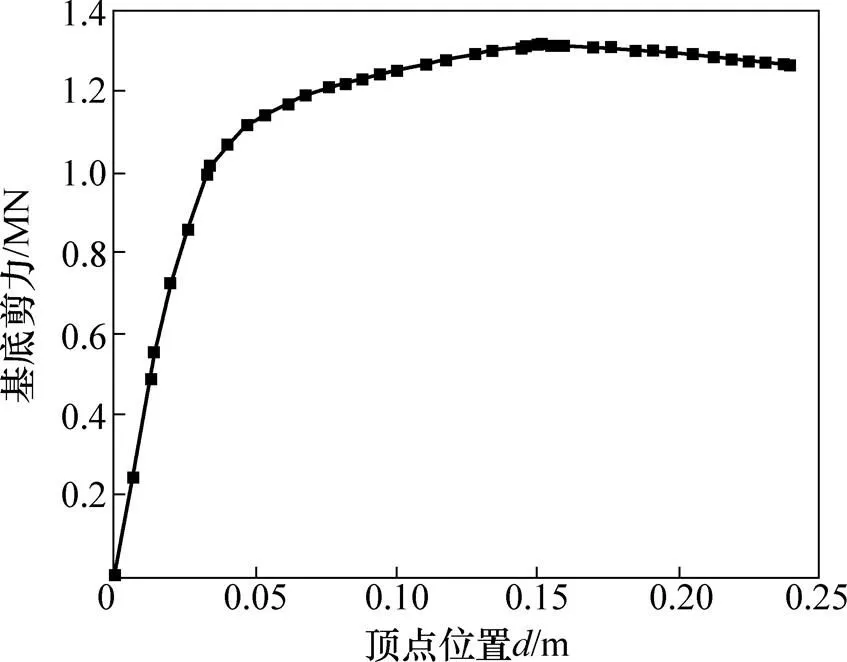
图16 塑性铰法Pushover曲线

图17 钢筋混凝土框架结构竖向位移云图
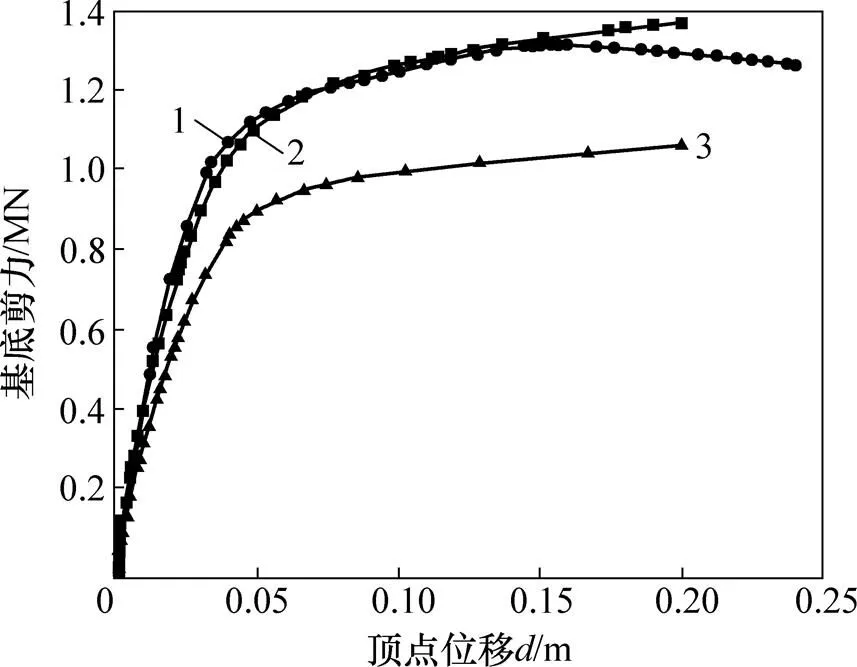
1—考虑楼板效应的整体模型法;2—考虑楼板效应的塑性铰法;3—未考虑楼板效应的整体模型法。
5 结论
1) 考虑楼板效应后梁端塑性铰曲线和未考虑楼板效应梁端塑性铰曲线差异明显,因此,进行有限元模型分析时应充分考虑现浇楼板的作用。
2) 采用塑性铰法计算得到的Pushover曲线与整体模型法计算得到的Pushover曲线吻合良好,说明塑性铰法能够有效地对楼板的作用效应进行模拟。
3) 该方法尚存在以下局限性:未考虑梁端塑性铰产生后强化阶段梁端弯曲刚度的变化。塑性铰属性修正系数取值与梁端截面面积和配筋直接相关,若将塑性铰法应用于工程中,则首先需弄清塑性铰修正系数与截面面积和配筋之间的对应关系。
[1] 王素裹, 韩小雷, 季静. 现浇楼板对RC框架结构破坏形式的影响分析[J]. 土木建筑与环境工程, 2009, 31(1): 66−71. WANG Suguo, HAN Xiaolei, JI Jing. The effect of slabs on the failure mode of reinforced concrete frame structures[J]. Journal of Civil Architectural and Environmental Engineering, 2009, 31(1): 66−71.
[2] 阎红霞, 杨庆山, 李吉涛. 现浇楼板对钢筋混凝土框架结构在地震作用下破坏形式的影响[J]. 振动与冲击, 2011, 30(7): 227−232. YAN Hongxia, YANG Qingshan, LI Jitao. Influence of cast-in-place floor slab on damage style of frame structures under earthquake[J]. Journal of Vibration and Shock, 2011, 30(7): 227−232.
[3] 单慧敏, 戴君武, 王艳茹. 现浇楼板对钢筋混凝土框架结构破坏模式影响浅析[J]. 土木工程学报, 2010(S1): 169−172. SHAN Huimin, DAI Junwu, WANG Yanru. Effects of casting slabs on the failure mode of RC frame structure[J]. China Civil Engineering Journal, 2010(S1): 169−172.
[4] 汪小林, 顾祥林, 印小晶, 等. 现浇楼板对钢筋混凝土框架结构倒塌模式的影响[J]. 建筑结构学报, 2013, 34(4): 23−31+42. WANG Xiaolin, GU Xianglin, YIN Xiaojing, et al. Effect of cast-in-situ floor slab on collapse modes of RC frame structures under earthquake[J]. Journal of Building Structures, 2013, 34(4): 23−31+42.
[5] 林旭川, 潘鹏, 叶列平, 等. 汶川地震中典型RC框架结构的震害仿真与分析[J]. 土木工程学报, 2009, 42(5): 13−20. LIN Xuchuan, PAN Peng, YE Lieping, et al. Analysis of the damage mechanism of a typical RC frame in Wenchuan earthquake[J]. China Civil Engineering Journal, 2009, 42(5): 13−20.
[6] PANTAZOPOULOU S J, FRENCH C W. Slab participation in practical earthquake design of reinforced concrete frames[J]. ACI Structural Journal, 2001, 98(4): 479−489.
[7] SHAHROOZ B M, PANTAZOPOULOU S J, CHERN S P. Modeling slab contribution in frame connections[J]. Journal of Structural Engineering, 1992, 118(9): 2475−2494.
[8] QIAN Kai, LI Bing. Quantification of slab influences on the dynamic performance of RC frames against progressive collapse[J]. Journal of Performance of Constructed Facilities, 2015, 29(1), 04014029.
[9] REN Peiqi, LI Yi, ZHOU Yulong, et al. Experimental study on the progressive collapse resistance of RC slabs[J]. Structures Congress, 2014, 4: 868−879.
[10] DAT P X, TAN K H. Experimental response of beam-slab substructures subject to penultimate-external column removal[J]. Journal of Structural Engineering, 2015, 141(7): 1−13.
[11] ALEMDAR B N, WHITE D W, LEON R T. Frame analysis including 3D slab effects in partially-restrained composite connections[J]. Composite Construction in Steel and Concrete IV, 2000, 4: 262−273.
[12] 刘源, 辛力, 王敏, 等. 框架梁刚度放大系数对结构的影响及合理取值[J]. 长安大学学报, 2013, 33(5): 64−68. LIU Yuan, XIN Li, WANG Min, et al. Reasonable value of rigidity amplification factor of frame beams[J]. Journal of Chang’an University, 2013, 33(5): 64−68.
[13] 朱磊, 张少钦, 戴宁, 等. 现浇楼板对RC框架结构动力特性影响的有限元分析[J]. 南昌航空大学学报, 2014, 28(3): 99−104. ZHU Lei, ZHANG Shaoqin, DAI Ning, et al. The finite element analysis of the influence of cast-in-place floor on the dynamic characteristics of RC frame structure[J]. Journal of Nanchang Hangkong University, 2014, 28(3): 99−104.
[14] 刘洪波, 徐龙军, 张庆国, 等. 考虑楼板影响的钢框架结构节点域数学模型[J]. 哈尔滨工业大学学报, 2012, 44(2): 28−32. LIU Hongbo, XU Longjun, ZHANG Qingguo, et al. Models for panel zones in steel moment frame structures with composite action[J]. Journal of Harbin Institute of Technology, 2012, 44(2): 28−32.
[15] 陶慕轩, 聂建国. 考虑楼板空间组合作用的组合框架体系设计方法(Ⅰ): 极限承载能力[J]. 土木工程学报, 2012, 45(11): 39−50. TAO Muxuan, NIE Jianguo. Design methods of composite frame systems considering the slab spatial composite effect (PartⅠ): ultimate loading capacity[J]. China Civil Engineering Journal, 2012, 45(11): 39−50.
[16] 陶慕轩, 聂建国. 考虑楼板空间组合作用的组合框架体系设计方法(Ⅱ): 刚度及验证[J]. 土木工程学报, 2013, 46(2): 42−53. TAO Muxuan, NIE Jianguo. Design guidelines of composite frame systems considering the slab spatial composite effect (PartⅡ): stiffness and verifications[J]. China Civil Engineering Journal, 2013, 46(2): 42−53.
(编辑 陈爱华)
Seismic performance analysis of RC frame structures with cast-in-place slab by plastic hinge method
SUN Wei, HUANG Yansheng
(College of Civil Engineering and Transportation,South China University of Technology, Guangzhou 510640, China)
In the seismic performance of reinforced concrete (RC) frame structure, the slab effect has a strong influence on the analysis results. The traditional solution method is to use the solid element to build the integral model, which needs a complicated model and costs a lot of computational time. For improving the efficiency of modeling and analysis, plastic hinge method was proposed. Plastic hinge method used the frame element to build the model and simulate the slab effect by modifying the plastic hinge property. The modified plastic hinge property data were calculated from the combined models of beam components and slab components. Plastic hinge method was applied to estimate the seismic performance of a two-story typical RC frame. The results show that compared with the traditional method, plastic hinge method is an effective method of the slab effect simulation.
reinforced concrete frame structure; seismic performance; slab effect; plastic hinge property
10.11817/j.issn.1672−7207.2017.08.028
TU375.4
A
1672−7207(2017)08−2187−08
2016−10−12;
2016−12−29
国家自然科学基金资助助项目(51008085)(Project (51008085) supported by the National Natural Science Foundation of China)
黄炎生,博士,教授,从事既有建筑物的可靠性评估研究;E-mail:cvyhuang@scut.edu.cn

