20CrMnTi材料成分波动对齿轮渗碳淬火性能的影响
张星,唐进元
20CrMnTi材料成分波动对齿轮渗碳淬火性能的影响
张星1, 2,唐进元1, 2
(1. 中南大学机电工程学院,湖南长沙,410083;2. 中南大学高性能复杂制造国家重点实验室,湖南长沙,410083)
通过有限元方法,探讨材料成分波动对齿轮渗碳淬火工艺性能的影响。以20CrMnTi半轴齿轮作为研究对象,利用JMATPRO软件,根据材料的化学元素波动的最大值与最小值分别建立2组材料性能数据库;基于DEFORM-HT软件,建立适用于渗碳淬火工艺的仿真数学模型,并对这2组材料性能数据库下的半轴齿轮分别进行渗碳淬火工艺仿真,对比分析齿轮渗碳淬火仿真后的各项参数。研究结果表明:材料成分波动对齿轮渗碳层影响较小,对淬火后相组织分布和齿轮变形量有较大影响。
20CrMnTi;半轴齿轮;渗碳淬火仿真;DEFORM-HT软件;JMATPRO软件
在现代齿轮制造过程中,硬齿面渗碳淬火已成为热处理主导工艺,深入理解渗碳淬火的相变和变形机制,不断优化渗碳淬火工艺路线,是提高齿轮热处理质量的前提与基础。渗碳淬火具有耗时长、费用高的特点,而随着计算机技术和数值计算理论的发展,一些较好的热处理仿真软件开发包也得到发展,使得人们完全可以对金属零件的热处理进行一定范围内的模拟仿真,如ANSYS[1],NSG ELTA[2],ABAQUS[3],FLUX[4],HEARTS和COSMAP[5−7]等。毫无疑问,计算机仿真技术是未来推动热处理技术发展的强劲动力。相对于淬火仿真而言,渗碳淬火的仿真较少,主要是因为渗碳淬火模拟更复杂[8]。LI等[9]利用DANTE分析了AMS 6308齿轮渗碳淬火后残余应力的分布以及影响因素,对比了不同渗层深度对残余应力生成的影响,最后用单齿弯曲和动态接触应力分析探讨了残余应力对疲劳寿命的影响。SUGIANTO等[10−11]利用DEFORM-HT软件对SCr420H斜齿轮渗碳淬火仿真进行了持续性研究,分析了相变塑性对齿轮变形和残余应力的影响。KIM等[12]利用有限元法对SCM415H斜齿轮渗碳淬火进行了仿真分析,并着重研究了扩散时间和淬火温度对齿轮变形的影响。研究表明,材料的化学成分对钢的热处理性能尤其是对合金钢淬透性产生较大影响[13−14]。目前,利用有限元方法研究材料成分波动对齿轮热处理性能的影响较少,为此,本文作者结合20CrMnTi半轴齿轮的渗碳淬火工艺,分析有限元方法下材料成分波动对齿轮渗碳淬火性能的 影响。
1 2组20CrMnTi材料性能数据库的建立
20CrMnTi材料的成分如表1所示。取第1组材料性能数据库的所有元素质量分数为最小值(即材料淬透性最低),建立的材料库以20CrMnTiL表示;第2组的所有元素质量分数取最大值(即材料淬透性最高),建立的材料库以20CrMnTiH表示。通过JMATPRO软件[15]建立适用于渗碳淬火工艺的20CrMnTiL和20CrMnTiH材料性能数据库。

表1 20CrMnTi材料成分(质量分数)
2 渗碳淬火数学模型的建立
渗碳淬火数学模型由4部分组成:1) 渗碳场模型,用于分析渗碳阶段的碳原子在齿轮中的扩散情况;2) 温度场模型,主要用于分析整个工艺过程中齿轮传热情况;3) 相变动力学分析,用于描述整个工艺过程中的相变;4) 应力应变模型,主要用于描述渗碳淬火后齿轮的残余应力和变形情况。
2.1 渗碳场模型
在强渗和扩散阶段,假设实际渗碳为非稳态情况,常用的基本控制方程为菲克第二定律。
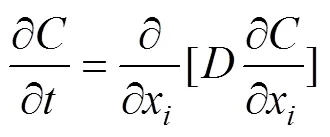
其中:,和x分别为含碳量、渗碳时间和沿扩散方向的距离;为碳原子在铁基合金中的扩散系数,一般取为温度和含碳量的函数[16],

和0.4分别为温度和碳的质量分数为0.4%时的扩散常数;为反应扩散系数与碳浓度之间关系的常数;和分别为碳原子扩散激活能和气体常数。取0.4=25.5 mm2/s,= 141 kJ/mol,=0.8。
碳原子扩散边界条件为

其中,e和s分别表示渗碳过程中反应炉中实际含碳量和齿轮表面含碳量(质量分数);为碳原子传递系数,反映了在表面进行化学反应速度。将阿累尼乌斯提出的关于化学反应速度与温度的关系应用于传递过程,即


表2 不同湿度下20CrMnTi的扩散系数
其中:β和分别为常数和激活能,取0=0.0034 7 mm/s,=34 kJ/mol。
2.2 温度场模型
温度场模型采用考虑到相变潜热影响的热传导模型[10]:
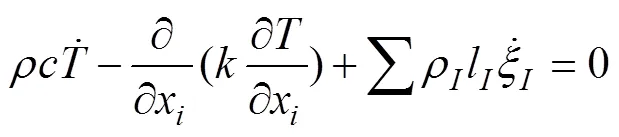
其中:,和分别为密度、比热容和导热系数。所有这些参数均为基于相态的温度函数;I为由相变所引起的潜热。图1和图2所示分别为20CrMnTiL材料性能数据库的比热容和导热系数与温度的关系。对于潜热计算,KANG等[17]提出了扩散模型的潜热计算,ERICSSON提出了非扩散模型的潜热计算公式。基于这2种计算方法,可以得到A→F,A→P,A→B和A→M所需的相变潜热分别为5.9×108,6.0×108,6.2×108和6.4×108J/m3。
1—奥氏体;2—铁素体;3—珠光体−贝氏体;4—马氏体。
图1 20CrMnTiL比热容与温度的关系
Fig. 1 Relationship between specific heat of 20CrMnTiL and temperature
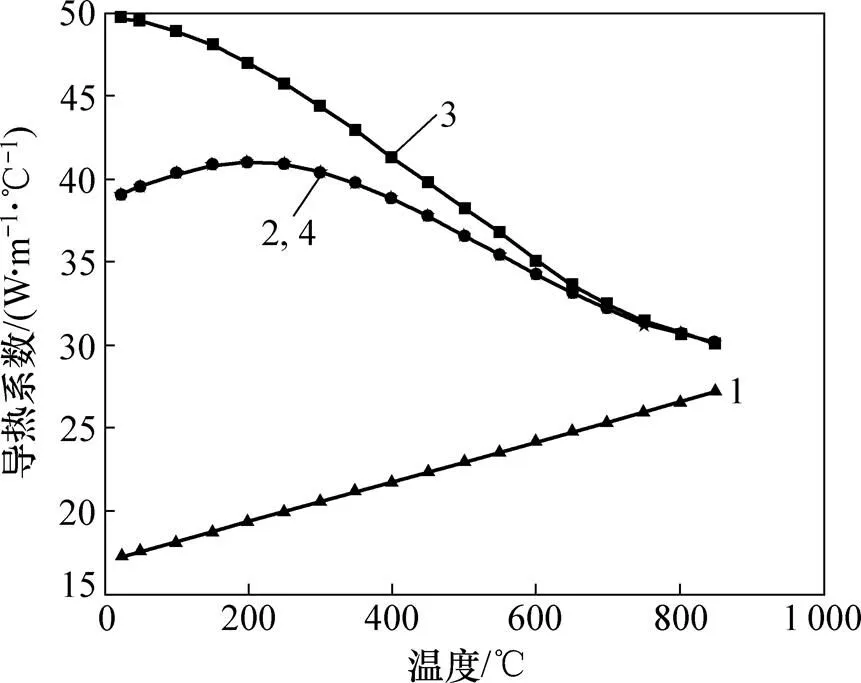
1—奥氏体;2—铁素体;3—珠光体−贝氏体;4—马氏体。
齿轮表面和外界进行热传递的边界条件为[10]
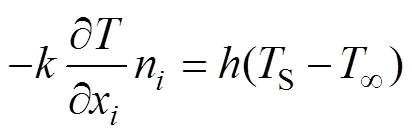
其中:h为换热系数,一般为表面温度的函数;TS和T∞分别为齿轮表面温度和外界温度。在淬火阶段,换热系数可认为是齿轮和淬火油的对流换热系数。采用张立文等[18]在2号分级油中实测的20CrMnTi钢对流换热系数作为仿真参数,如图3所示。
2.3 相变动力学分析
在渗碳阶段前的加热阶段,齿轮初始相组织奥氏体化的过程采用简化扩散方程计算:
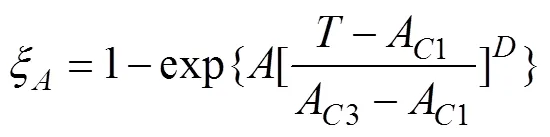
其中:ξ为生成的奥氏体体积分数;和为材料常数,通常取为−4和2;为单元平均热力学温度;C1和C3分别为奥氏体相变开始和终了温度点,可从CCT曲线中得到。
在淬火和空冷阶段,奥氏体向其他组织转变。对于扩散型相变,如铁素体、珠光体转变和贝氏体转变,其转变体积分数的计算一般通过Johnson-Mehl方程计算[19]:

其中:和分别为材料常数,可以从TTT曲线图中得到。对于非扩散型转变即马氏体转变,习惯上用K-M方程预测。
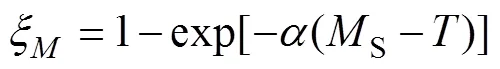
其中:S为马氏体转变起始点;为应力的函数,通过TTT曲线图计算得到,取为含碳量的函数。所有的相变动力学参数均通过JMATPRO软件计算得到的CCT/TTT曲线得出。考虑到渗碳工艺,传统的相变动力学曲线图无法满足渗碳淬火工艺,需将曲线图取为含碳量的函数,本文分别取含碳量(质量分数)为0.2%,0.4%,0.6%,0.8%和1.0%这5种状态计算动力学 参数。
2.4 应力应变模型
塑性流动应力的计算取决于各个相组织的流动应力曲线。其模型考虑应变、应变速率和温度的影 响[20−21]。
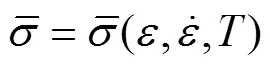
在应力应变计算模型中,对于应变速率的计算需考虑热应变、弹性应变、塑性应变以及相变和相变塑性的影响。表达方程如下:
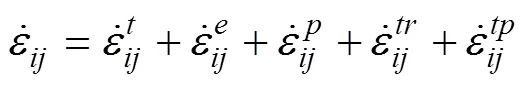

1—奥氏体;2—铁素体;3—珠光体−贝氏体;4—马氏体。

1—奥氏体;2—铁素体;3—珠光体−贝氏体;4—马氏体。
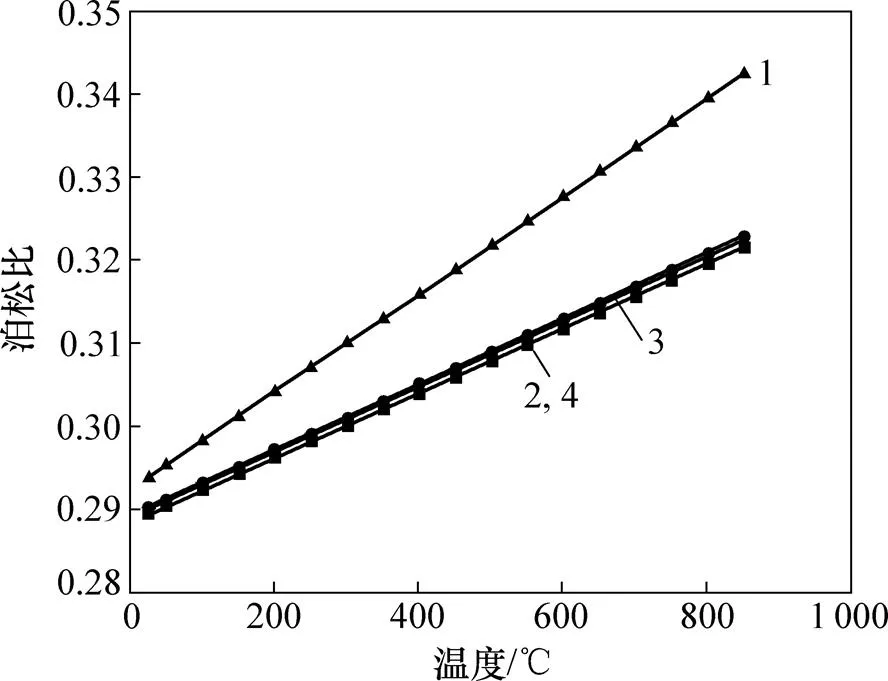
1—奥氏体;2—铁素体;3—珠光体−贝氏体;4—马氏体。
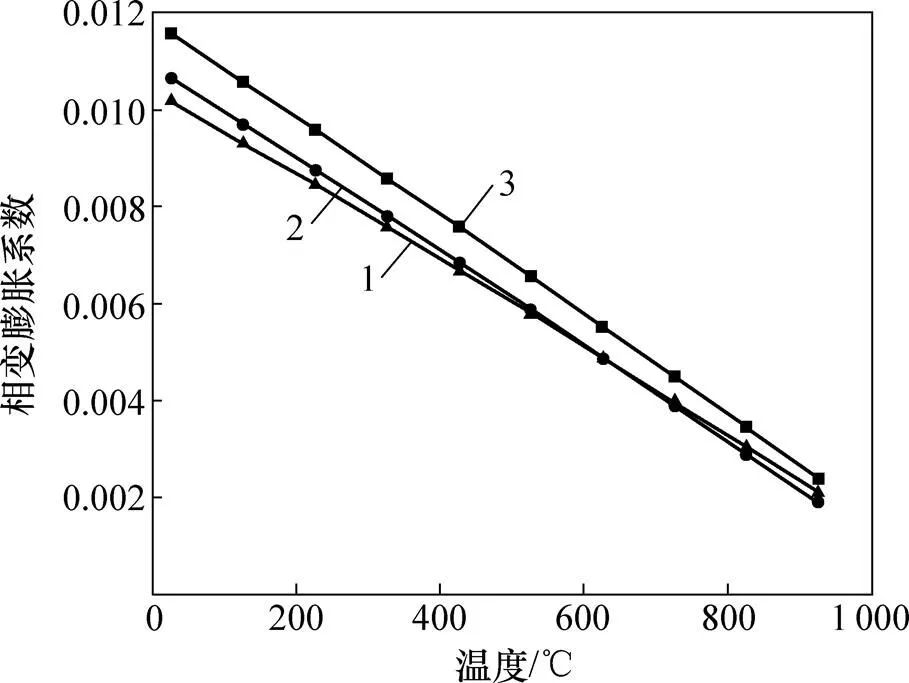
1—A→F;2—A→BP;3—A→B。

1—A→F;2—A→BP;3—A→B。
3 有限元模型及工艺曲线的确定
3.1 齿轮有限元模型确定
分析齿轮为汽车用差速器半轴齿轮。考虑到零件模型较大,导入全部模型计算耗费时间过长,本文分别取模型的1/4以及单齿的1/2进行仿真分析,其有限元模型如图9所示。

(a) 差速器半轴齿轮1/4模型;(b) 差速器半轴齿轮1/2齿模型
3.2 热处理工艺的确定
根据实际半轴齿轮渗碳淬火工艺,确定仿真工艺曲线如图10所示。
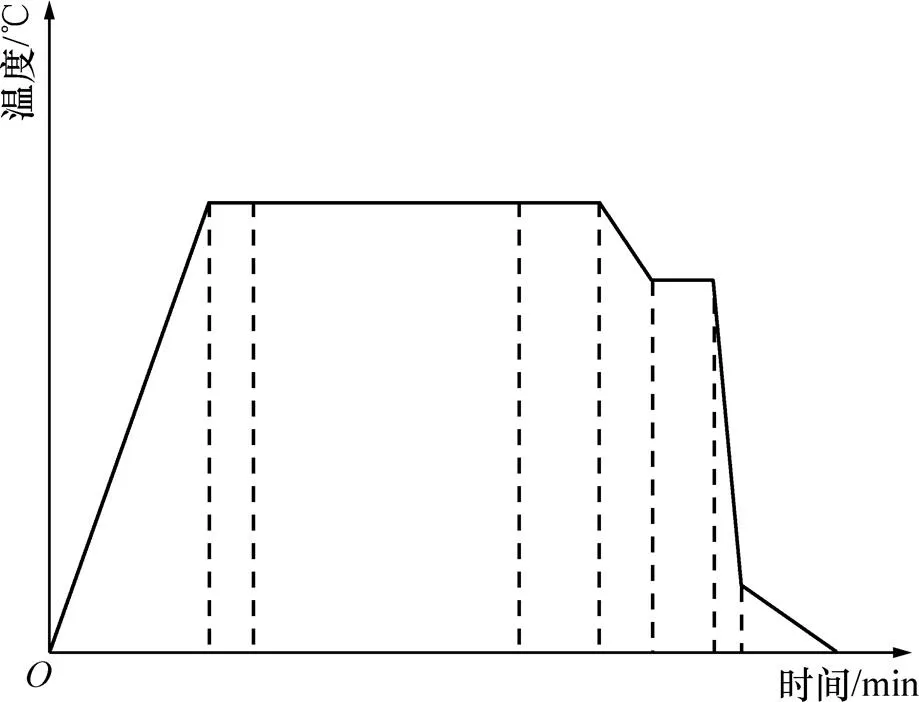
图10 渗碳淬火仿真工艺曲线
4 结果分析
4.1 碳质量分数分布
工艺决定表层含碳量的分布情况。表层含碳量分布对轮齿的表层硬度和抗疲劳强度等都有很大影响。图11和图12所示为20CrMnTiL和20CrMnTiH的1/2轮齿模型含碳量(质量分数)分布测量位置及分布。
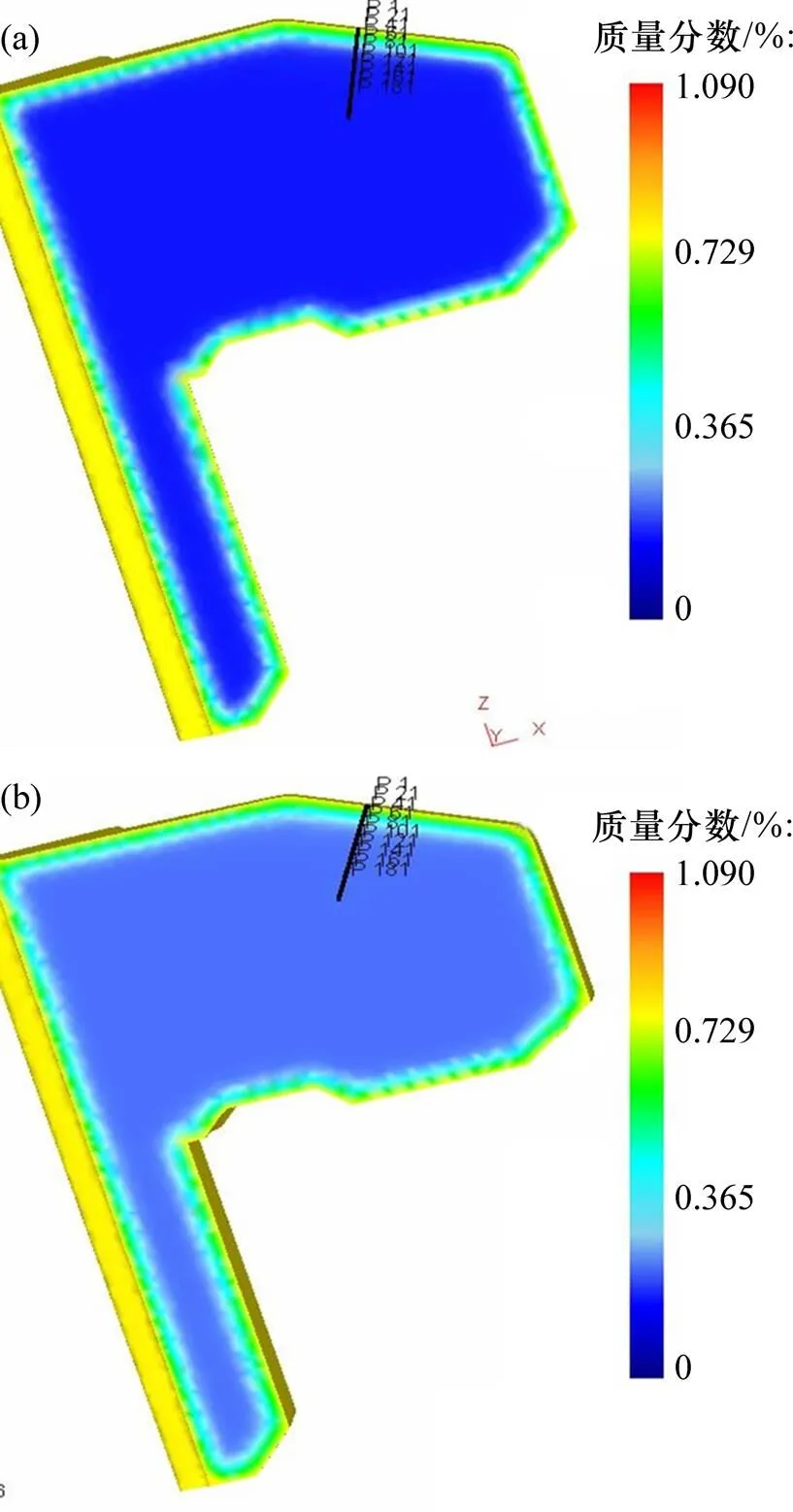
(a) 20CrMnTiL;(b) 20CrMnTiH
从图12 可得:强渗结束后轮齿表面最高含碳量约为1.09%;在扩散阶段完成后,轮齿表面含碳量约为0.8%;扩散结束后,轮齿由表面到心部的含碳量变化曲线整体趋于平缓,未出现含碳量梯度过陡的现象。对比分析渗碳后20CrMnTiL和20CrMnTiH这2种材料库下模型的含碳量分布曲线发现材料成分的波动对轮齿渗碳的影响并不明显,其差别可以忽略。
4.2 淬火相组织分布
图13所示为20CrMnTiL马氏体体积分数分布。从图13可得:以20CrMnTiL作为材料库时,淬火后轮齿主要成分为马氏体组织,轮齿心部马氏体体积分数较少,约为70%。这是因为中间部位冷却速率较小,有扩散型相变发生,奥氏体并未完全进行马氏体转变。
图14所示为以20CrMnTiH作为材料库得到的马氏体体积分数分布。从图14可知:淬火后轮齿整体几乎全部为马氏体组织,心部的马氏体组织体积分数同样达到90%以上,大大高于图13中心部马氏体体积分数,这主要是因为20CrMnTiH材料库相对于20CrMnTiL而言,其含碳量更高,合金成分质量分数也高,导致其淬火临界冷却速度降低,淬透性提高,因此,心部发生扩散型转变的可能性降低。

(a) 20CrMnTiL;(b) 20CrMnTiH
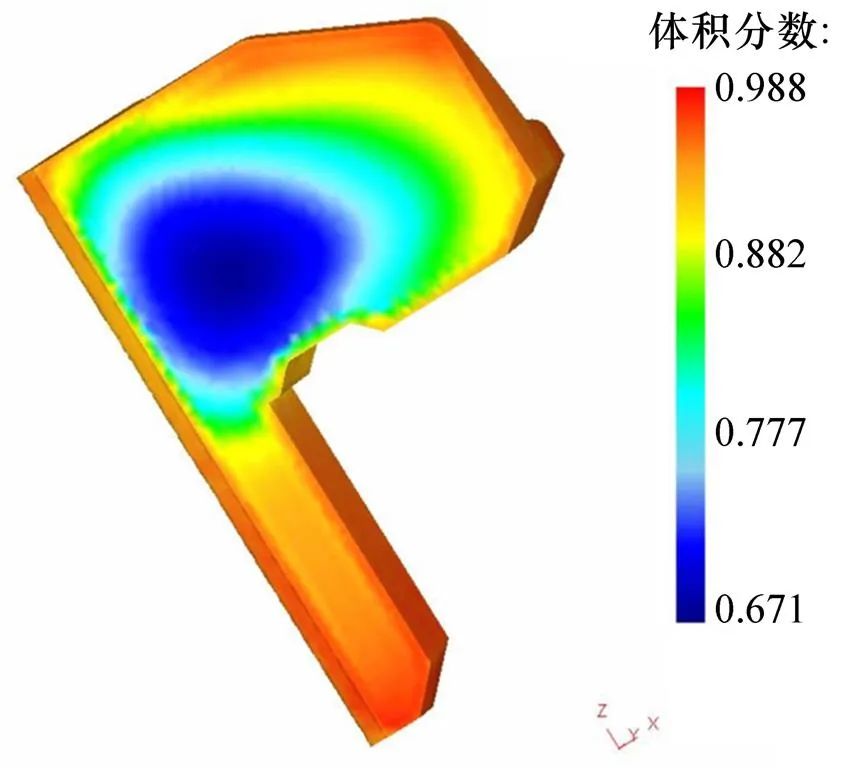
图13 20CrMnTiL 马氏体体积分数分布
图15所示为以20CrMnTiL作为材料库时轮齿贝氏体体积分数分布。从图15可知:轮齿心部在淬火过程中有贝氏体转变发生,其最大转变量为32%左右。这是由于20CrMnTiL材料库的含碳量和合金成分都较低,使得TTT曲线图中临界冷却速度较高,增大了扩散型转变发生的可能性,从而使得心部位置有较多贝氏体生成。贝氏体组织相对于马氏体组织硬度偏低,这也是该种材料库下轮齿心部硬度较低的原因。
图16所示为以20CrMnTiH作为材料库时,轮齿淬火后的贝氏体分布。从图16可知:轮齿靠近边缘部分几乎没有贝氏体生成,轮齿中间也只有约8.7%的贝氏体产生,这是20CrMnTiH的临界冷却速度较低所致。无论是采用淬透性最差的20CrMnTiL材料库还是采用淬透性最好的20CrMnTiH材料库,在淬火仿真中均未有铁素体、珠光体产生。
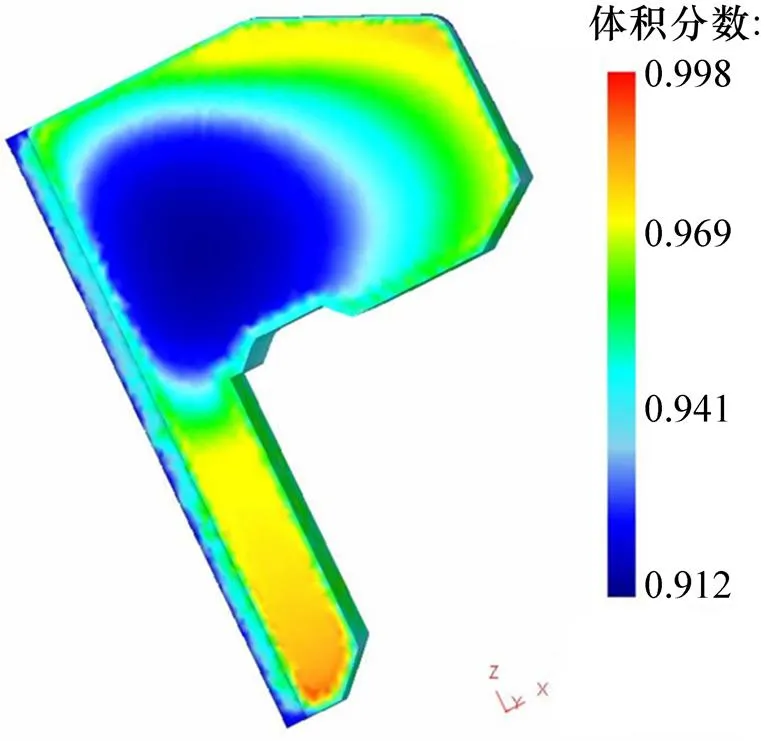
图14 20CrMnTiH马氏体体积分数分布

图15 20CrMnTiL贝氏体体积分数分布
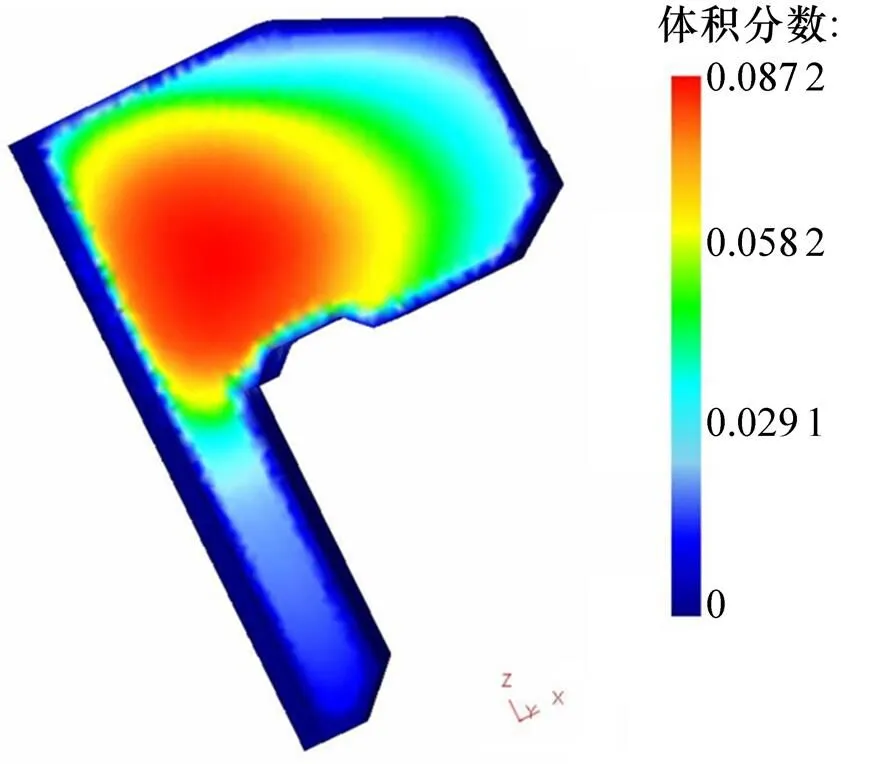
图16 20CrMnTiH贝氏体体积分数分布
4.3 径向变形分析
该半轴齿轮主要变形问题是花键径向变形量不均匀,锥度较大[22]。本文在变形分析时选取花键径向变形量作为分析对象。
齿轮淬火后径向变形(20CrMnTiL)见图17。从图17可知:以20CrMnTiL为材料库时,其内花键径向变形为−0.067 9~−0.009 6 mm。其中,靠近齿端处内花键收缩量较小,约为−0.010 0 mm;靠近轴端处内花键收缩量较大,为−0.068 0 mm左右。这主要是因为靠近齿端处的心部在较高温度时有贝氏体转变发生,贝氏体的生成不仅使得该部位奥氏体质量分数减小(奥氏体的膨胀系数较大,冷却时会造成零件较大收缩),同时,贝氏体的稳定性更强,抗塑性变形能力增强,从而抑制了该部位的收缩现象。反观齿轮靠近轴端的部位,由于体积较小,热交换面积大,冷却速度较快,该处内外均为马氏体组织,而马氏体组织需在较低温度下生成(此时奥氏体冷却收缩现象严重),从而造成内花键明显收缩。
齿轮淬火后20CrMnTiH的径向变形见图18。从图18可知:以20CrMnTiH为材料库时,其内花键径向变形量为−0.076 6~0.012 0 mm,且内花键靠近齿端位置有膨胀趋势,膨胀量约为0.012 0 mm。这是因为该位置心部少量贝氏体在有效抑制收缩趋势的同时,大量马氏体的生成促进了齿轮的膨胀变形。而靠近轴端处收缩量更大,因为相对于20CrMnTiL材料库,20CrMnTiH材料库中的奥氏体相具有更大的热膨胀系数和更低的马氏体转变起始温度。材料成分波动引起的径向偏差见表3。
从表3可知:以20CrMnTiL作为材料库时,内花键径向变形引起的锥度(内花键齿顶径向波动范围)为0.058 3 mm;以20CrMnTiH作为材料库时,内花键径向变形引起的锥度为0.088 6 mm,内花键的锥度控制指标为0.080 0 mm。换言之,即使不考虑其他任何不确定因素(如热前机加工残余应力、齿轮初始组织均匀性、齿轮不同位置材料成分均匀性)对内花键径向变形的影响,由材料成分波动对变形的影响占控制指标值的73%~111%。这对控制内花键锥度是极其不利的,需更换材料或者改变齿轮现有装夹状态。

表3 材料成分波动引起的径向偏差
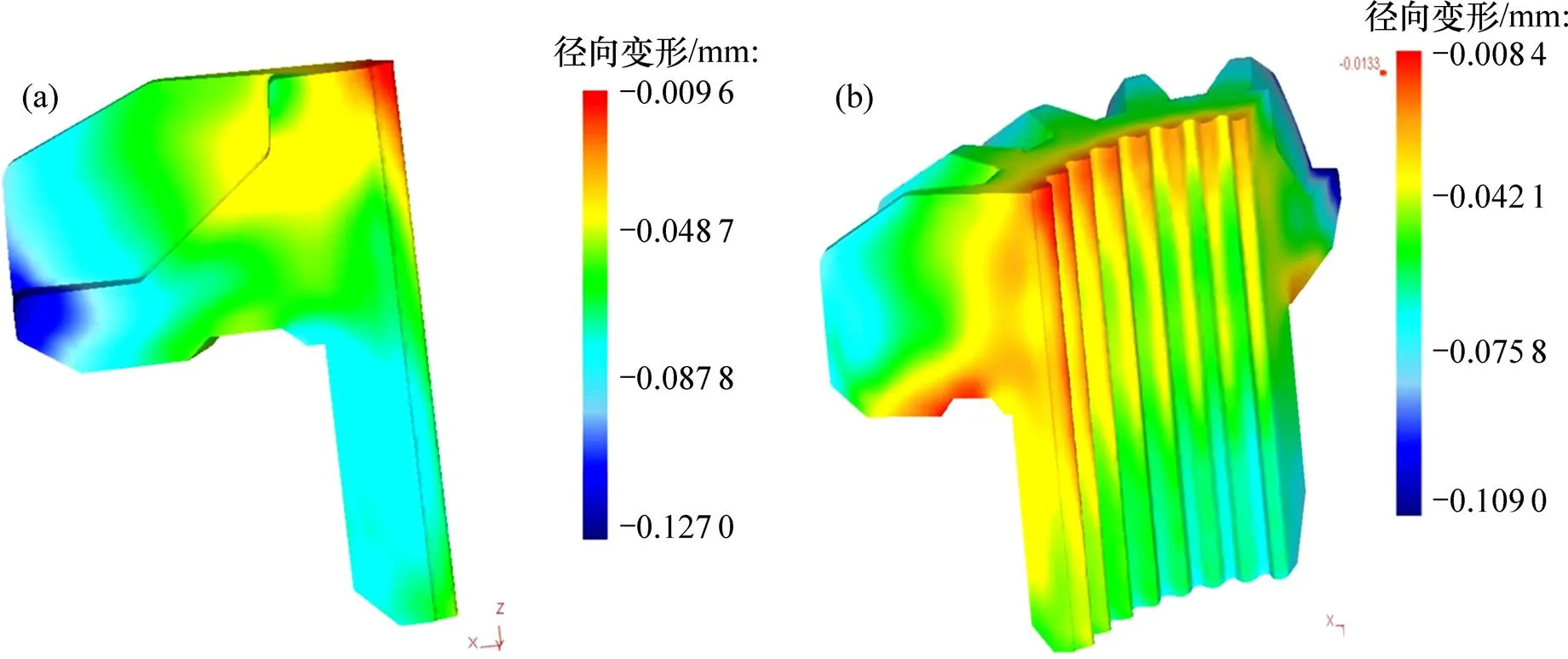
(a) 1/2轮齿模型淬火后径向变形;(b) 1/4齿轮模型淬火后径向变形

(a) 1/2轮齿模型淬火后径向变形;(b) 1/4齿轮模型淬火后径向变形
5 结论
1) 对比分析2组材料库下齿轮的表面渗层情况,两者并无明显差别,即材料成分的波动对表层渗碳的基本没有影响。
2) 对比分析2组材料库下齿轮的淬火相组织分布,齿轮淬火后组织主要为马氏体,以20CrMnTiL作为材料库时,轮齿心部马氏体质量分数约为70%,贝氏体组织约为30%;以20CrMnTiH作为材料库时,轮齿心部马氏体组织在90%以上,贝氏体组织质量分数低于10%。这是由于20CrMnTiH相对于20CrMnTiL材料库合金元素质量分数更高,有效地降低了临界冷却速度,减小了扩散型相变的发生。
3) 半轴齿轮的内花键径向变形不均匀,靠近齿部收缩量较小,靠近轴部收缩量较大。对比2组材料库下内花键径向变形量,以20CrMnTiH作为材料库时,内花键径向变形趋势更加强烈。
4) 由材料成分波动导致的内花键锥度波动为0.058 3~0.088 6 mm,达到或超过内花键锥度控制指标,需更换材料或者改变齿轮现有装夹状态。
[1] BUI H T, HWANG S J. Modeling a working coil coupled with magnetic flux concentrators for barrel induction heating in an injection molding machine[J]. International Journal of Heat and Mass Transfer, 2015, 86(3): 16−30.
[2] IVANOV D, MARKEGARD L. Simulation of stress and strain for induction-hardening applications[J]. Journal of Materials Engineering and Performance, 2013, 22(11): 3258−3268.
[3] SCHWENK M, HOFFMEISTER J. Experimental determination of process parameters and material data for numerical modeling of induction hardening[J]. Journal of Materials Engineering and Performance, 2013, 22(7): 1861−1870.
[4] COUPARD D, PALIN-LUC T. Residual stresses in surface induction hardening of steels: comparison between experiment and simulation[J]. Materials Science and Engineering A, 2008, 487(1/2): 328−339.
[5] JU D Y, LIU C C. Overview on the microstructure evolution and induced stresses in nitrided chromium steels[C]//The 9th International Seminar Nitriding Technology, Institute of Precision Mechanics. Warsaw, Poland, 2003: 299−309.
[6] JU D Y, LIU C C, INOUE T. Numerical modeling and simulation of carburized and nitrided quenching process[J]. Journal of Materials Processing Technology, 2003, 143/144(26): 880−885.
[7] MUKAI R, MATSUMOTO T, JU D Y. Modeling of numerical simulation and experimental verification for carburizing- nitriding quenching process[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(S1): 566−571.
[8] SONG Gangsheng, LIU Xianghua, WANG Guodong. Numerical simulation on carburizing and quenching of gear ring[J]. Journal of Iron and Steel Research, International, 2007, 14(6): 47−52.
[9] LI Zhichao, FREBORG A M. Modeling the effect of carburization and quenching on the development of residual stresses and bending fatigue resistance of steel gears[J]. Journal of Materials Engineering and Performance, 2013, 22(4): 664−672.
[10] SUGIANTO A, NARAZAKI M, KOGAWARA M. Numerical simulation and experimental verification of carburizing- quenching process of SCr420H steel helical gear[J]. Journal of Materials Processing Technology, 2009, 209(7): 3597−3609.
[11] SUGIANTO A, NARAZAKI M, KOGAWARA M. Distortion analysis of axial contraction of carburized-quenched helical gear[J]. Journal of Materials Engineering and Performance, 2010, 19(2): 194−206.
[12] KIM N K, BAE K Y. Analysis of deformation in the carburizing-quenching heat treatment of helical gears made of SCM415H steel[J]. International Journal of Precision Engineering and Manufacturing, 2015, 16(1): 73−79.
[13] 丁峰, 张焱. 合金元素对钢热处理的影响[J]. 热处理, 2007, 22(1): 63−67. DING Feng, ZHANG Yan. Effect of alloy elements on heat treatment of steels[J]. Heat Treatment, 2007, 22(1): 63−67.
[14] 朱张校. 工程材料[M]. 3版. 北京: 清华大学出版社, 2001: 67−150. ZHU Zhangxiao. Engineering materials[M]. 3rd ed. Beijing: Tsinghua University Press, 2001: 67−150.
[15] SCHILLÉ J P, GUO Z L. Modeling phase transformations and material properties critical to processing simulation of steels[J]. Materials and Manufacturing Processes, 2011, 26(1): 137−143.
[16] 张星, 唐进元. 17CrNiMo6内齿圈渗碳仿真关键技术研究[J]. 金属热处理, 2015, 40(3): 185−189. ZHANG Xing, TANNG Jinyuan. Key technology in carburizing process simulation for 17CrNiMo6 steel annular gear[J]. Heat Treatment of Metals, 2015, 40(3): 185−189.
[17] KANG S H, IM Y T. Thermo-elastic-plastic finite element analysis of quenching process of carbon steel[J]. Journal of Materials Processing Technology, 2007, 192: 381−390.
[18] 张立文, 朱大喜, 王明伟. 淬火冷却介质换热系数研究进展[J]. 金属热处理, 2008, 33(1): 53−56. ZHANG Liwen, ZHU Daxi, WANG Mingwei. Development of research on heat-transfer coefficient for quenchant[J]. Heat Treatment of Metals, 2008, 33(1): 53−56.
[19] MAYNIER P, DOLLET J. Hardenability concepts with applications to steels[M]. DOANE D V, KIRKALDY J S. New York: AIME, 1978: 518−544.
[20] ŞIMŞIR C, GÜR C H. 3D FEM simulation of steel quenching and investigation of the effect of asymmetric geometry on residual stress distribution[J]. Journal of Materials Processing Technology, 2008, 207(1): 211−221.
[21] TOTTEN G, HOWES M, INOUE T. Handbook of residual stress and deformation of steel[M]. ASM International, 2002: 248−312.
[22] 陈葵, 黄星星, 刘坚. 带内齿和内花键的汽车齿轮热处理变形的控制方法[J]. 汽车工艺与材料, 2013(7): 34−38. CHEN Kui, HUANG Xingxing, LIU Jian. The heat treatment deformation control method for automotive gears with internal teeth and splines[J]. Automobile Technology & Material, 2013(7): 34−38.
(编辑 陈灿华)
Effect of 20CrMnTi material compositions fluctuation on gear performance after carburizing and quenching process
ZHANG Xing1, 2, TANG Jinyuan1, 2
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083,China;2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)
The discussion about the effect of 20CrMnTi material compositions fluctuation on gear carburizing-quenching performance was done using FEM. Taking 20CrMnTi side gear as the research object, two groups of material properties databases were set up according to the maximum and the minimum values of chemical elements fluctuation by JMATPRO software. Simulation mathematical model was built for carburizing-quenching process based on DEFORM-HT software. Some simulations were done for gear carburizing-quenching process with two material databases. Simulation results were compared. The results show that material compositions fluctuation has little impact on carburized layer, and has great impact on distribution of quenching phases and deformation of gear.
s: 20CrMnTi; side gear; carburizing-quenching simulation; DEFORM-HT software; JMATPRO software
10.11817/j.issn.1672−7207.2017.08.003
TG16
A
1672−7207(2017)08−1979−09
2016−09−10;
2016−11−12
国家自然科学基金资助项目(51535012,U1604255);湖南省重点研发计划项目(2016JC2001)(Projects (51535012, U1604255) supported by the National Science Foundation of China; Project (2016JC2001) supported by the Key Research and Development Project of Hunan Province)
唐进元,教授,博士生导师,从事齿轮热处理工艺及仿真研究;E-mail:jytangcsu@163.com

