过搓板路仿真与试验差异的主要因素分析
叶锦文,杨 蔓,段守焱
过搓板路仿真与试验差异的主要因素分析
叶锦文,杨 蔓,段守焱
(广州汽车集团股份有限公司 汽车工程研究院,广州 510640)
对比仿真与试验转向节轮心处受力在时域及频率的差异,以试验数据为基准分析衬套刚度、阻尼,动力总成系统,减振器阻尼及悬架KC特性等主要因素对仿真准确性的影响,然后改进模型并进行仿真分析,仿真结果与试验结果高度吻合,表明模型准确、可信。
搓板路;频域;时域;衬套刚度;阻尼;ADAMS
为了获得与实际相近的仿真结果,车辆动力学模型需要与试验对标。如果仿真与试验测试非常接近,则认为模型有很高的精准度,能反映实际车辆特性,模型能用于分析其他工况[1]。
搓板路的路面特征简单、有规律,容易建模,且路面激励的频率分布较广,是分析仿真与试验相关性的良好路面。如果过搓板路仿真与试验相关性高,意味着模型车辆对路面激励的响应在很宽的频域范围内是准确的。模型可用于其他特征路面的分析。
1 仿真准确性影响因素及建模
车辆是一个复杂的系统,影响整车仿真准确性的因素有很多。车辆不同位置对标的难易程度差别很大。通常轮心处转向节的载荷是必要的标定点。因为车辆激励的主要来源是路面,路面激励经过轮胎的减振传递至转向节,然后经过悬架等复杂的系统作用于车身。只有转向节的载荷与试验相符,车辆其他位置的对标才有意义。此外,轮心处转向节的载荷是车辆试验验证的必要的测量项目之一。转向节的载荷容易获取,有专用测试设备且精度较高。因此,与其他位置相比,转向节的载荷标定也相对简单、方便。
在车辆设计后期,车辆通常会在试验场采集道路载荷谱用于分析、验证零部件的强度、耐久等性能。道路载荷谱指路面激励引起的车辆结构相应信号,包含轮心六分力、加速度、应变、位移信号等。轮心六分力是道路载荷谱的采集内容之一。轮心六分力通过安装在车轮的六分力仪采集获得。因轮胎外倾角和前束的影响,安装六分力仪时需校正以减小或消除前束和外倾产生的误差。通常六分力仪采集的并不是轮心处的载荷(因仪器结构的限制),因此,转向节在轮心处的受力需经过换算才能得到。
转向节受到的载荷包含三个方向的力和力矩。其反作用力及力矩即轮毂受到转向节作用的载荷,该载荷与轮胎受到地面的力及力矩、车轮惯性力三者之间相互平衡。对于采用经过辨识的轮胎模型,若仿真转向节受力与试验测试吻合,则力矩与试验结果也能很好吻合。因此,论文只分析转向节受力仿真与试验测试的相关性。
本文研究的车型前悬为麦弗逊悬架,后悬为多连杆悬架。整车多体动力学模型用ADAMS/CAR软件建模。模型的车身是刚性的[2-3]。轮胎采用FTire模型。
汽车试验场搓板路由图1所示的轮廓单元重复而成。仿真路面根据图示的特征建模。为了获得足够长的力信号,路面模型的长度为200 m。车辆以40 km/h的速度过搓板路时,路面Z方向的激励频谱如图2所示。由图2可知,搓板路的激励频谱是离散的谱线,主要频率分布在10~60 Hz。这也是轮胎模型需要采用FTire或者更复杂的轮胎模型的原因。FTire有效的响应频率能达到120 Hz以上,能准确反映搓板路路面产生的激励[4-5]。
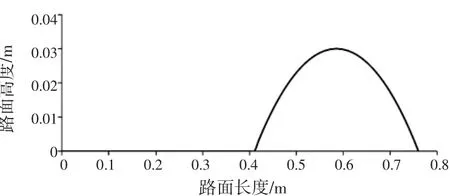
图1 搓板路路面轮廓单元
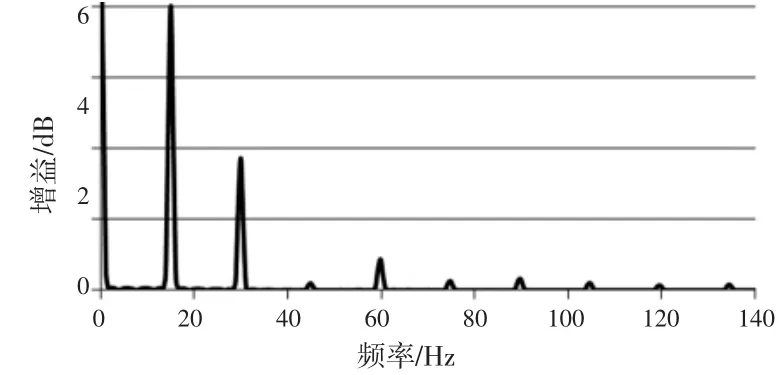
图2 搓板路激励频谱
2 过搓板路仿真及相关性分析
2.1 基于线性刚度衬套的仿真分析
在车型设计中期,已经有必要进行整车性能分析。这个阶段的设计参数已经齐全,但是通常不是很详细或很准确。典型的例子是衬套的刚度。这个阶段的衬套刚度通常是线性的,对于有限位结构的衬套通常还有限位信息。同时其他设计参数一般都是设计值,而非试验测量值。因此,论文首先分析基于理论设计参数的转向节轮心处受力,研究初期仿真分析的准确性。
时域上,前转向节受力对比如图3~图5所示。由图可知,转向节受力在仿真2.5 s后表现稳定,并且呈现周期性。这是因为搓板路产生的激励是周期性的。车辆从平路进入搓板路后,由初始条件产生的自由振动和伴随强迫振动发生的自由振动因阻尼的存在迅速衰减,车辆进入稳态[6]。试验因客观因素没法表现出非常明显的周期性,同时试验受力在8 s~13.5 s之间明显偏小。经分析,是因试验场的搓板路部分路段明显受损导致激励较小所致。由图3可知,前悬转向节X方向(整车坐标系)受力仿真明显小于试验。前悬转向节Y方向的受力差异更大,试验大约是仿真的4倍,如图4所示。前悬转向节Z方向的受力从峰峰值对比很接近(后转向节三个方向仿真与试验的峰峰值均很接近),如图5所示。但是,峰峰值接近并不意味着仿真与试验相关性好、吻合程度高,因为波形包含的频率成分可能有很大的差异。因此,有必要对轴节的受力作频谱分析。
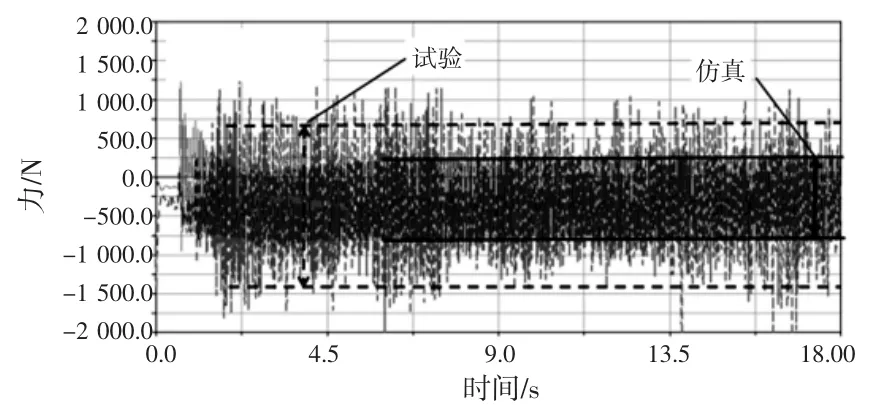
图3 前悬转向节FX时域对比
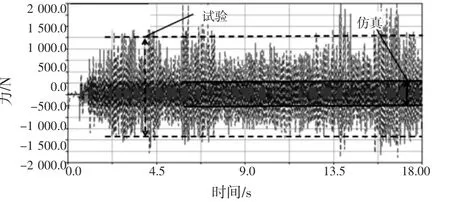
图4 前悬转向节FY时域对比
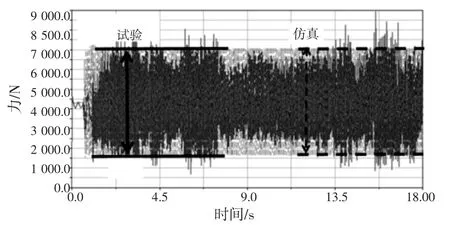
图5 前悬转向节FZ时域对比
因此,还需在频域对比分析轴节受力。频率与车速有关。车速越快,相同时间内经过的路面“拱形”越多,车轮受到的冲击次数越多,频率越高。车速越快则频率越慢。初始仿真车速可以根据试验车速输入,也可以根据搓板路的波长λ和频谱的一阶频率f计算得到:v=λf。其中,v是车速。
车辆驶入搓板路后需要经过一定的时间方能达到稳态并且试验场搓板路路面部分路段受损。非稳态部分使试验与仿真的频率分布难以很好地吻合,受损路段部分的因激励偏小使试验的幅值偏小。由于上述的原因,对时域数据做傅里叶变换时显然不能选取整个时间段,需截取其中稳定的非受损路段部分。这点对频谱分析很重要。
转向节受力的频谱分析表明:幅值上,前转向节Z方向仿真与试验高度吻合,如图6所示。前、后转向节其他方向均有较明显的差别。特别是后悬转向节X、Y方向的受力,在时域上峰峰值接近,但是频域上差异明显,如图7所示。这说明模型对某些频率激励的响应不准确,不能准确反映实际车辆的特性。

图6 前悬转向节FZ频域对比

图7 后悬转向节FY频域对比
2.2 仿真准确性影响因素分析
理论上,整车模型任何参数不准确都会降低仿真与试验相关性。事实上,有很多的参数产生的仿真误差很小,对工程分析没有影响。因此,文章主要讨论对仿真与试验相关性有较明显影响、不能忽略的建模参数。
车辆过搓板路本质上是一个复杂系统受到路面激励产生振动。根据振动理论,影响系统振动的因素有:质量、转动惯量、刚度及阻尼。摩擦也是阻尼中的一种。因此,转向节受力的影响因素主要是车辆各系统的质量、转动惯量、刚度及阻尼。零部件的质量和转动惯量可从数模获得,通常是比较准确的,本文不展开讨论。需要说明的是,因建模简化的原因,有些模型零件的重量实际上是几个零件重量之和。比如模型转向节的重量应该是实际的转向节重量和制动卡钳重量之和。整车的刚度和阻尼由各系统的刚度和阻尼组成,是一个复杂的系统。
轮胎的特性非常复杂,对搓板路仿真结果有很大影响。搓板路激励频率宽且较高,建议用Ftire或更精准的轮胎模型。准确的轮胎模型是保证仿真准确的前提条件。
悬架Z方向的系统刚度和阻尼主要由悬架刚度、减振器阻尼决定。其中,悬架刚度主要由弹簧刚度决定。衬套的刚度及阻尼对悬架Z方向的刚度、阻尼影响小。悬架刚度、减振器阻尼通常在设计阶段准确性就很高。因此,只要有准确的轮胎模型,悬架系统Z方向的刚度和阻尼很准确。因此,应用线性刚度的衬套和粗略估计的衬套阻尼就能使转向节Z方向获得关联性程度很好的结果。
悬架X、Y方向的系统刚度和阻尼主要由衬套共同决定。有的悬架摆臂刚度较小,摆臂的柔性变形和结构阻尼对X、Y方向的刚度和阻尼也有明显影响[7]。衬套和零件的刚度和阻尼都是复杂的。试验表明橡胶衬套的特点有:刚度非线性、静态摩擦(迟滞回线),动态特性跟幅值和频率有关。不同衬套变形量的幅频、相频特性分别如图8和图9所示。其中,幅值经常表述为动刚度,是包含阻尼力的复刚度;而相位角或滞后角则表征橡胶衬套的阻尼或能量损失[8-9]。因此,线性刚度衬套模型与实际有很大误差,如图10所示。
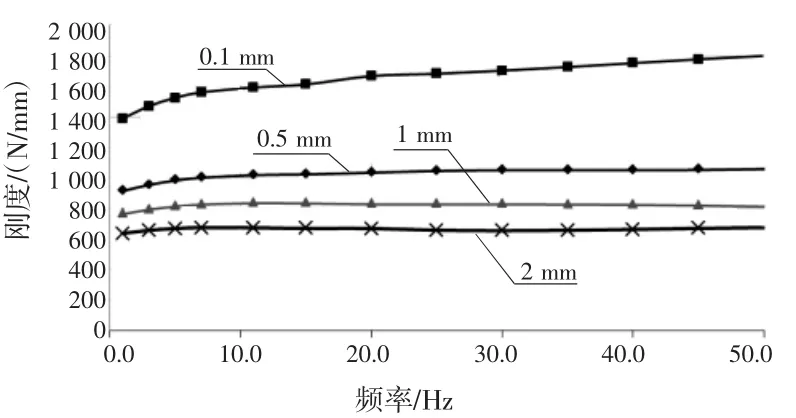
图8 衬套幅频特性
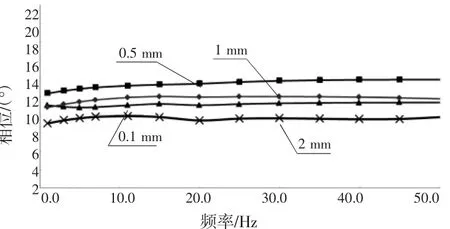
图9 衬套相频特性

图10 线性刚度衬套与实际衬套刚度对比
研究表明,前悬下摆臂后衬套Y向的刚度和阻尼对转向节X方向受力有显著影响,并且阻尼的影响更明显。后悬纵臂前衬套X方向的刚度和阻尼对后转向节X方向受力有显著影响,并且阻尼的影响更明显。这两个衬套的作用也是缓和车轮X方向的冲击,分别如图11和图12所示。阻尼的影响更显著是因为两个衬套在上述受力方向都是空心的,受力时变形较大。另一个原因是搓板路的激励频率较高。频率越高,阻尼的影响越明显。同理,其他主要承受Y向力衬套对转向节Y向受力影响明显。
综上所述,衬套的刚度和阻尼对转向节X、Y方向受力影响显著。为了提高仿真与试验的相关性,衬套模型最好能够体现动刚度特性。如果没有动刚度的衬套模型,可以用非线性刚度、线性阻尼的衬套模型。仿真结果表明,合适的线性阻尼、准确的非线性刚度可获得较准确的结果。
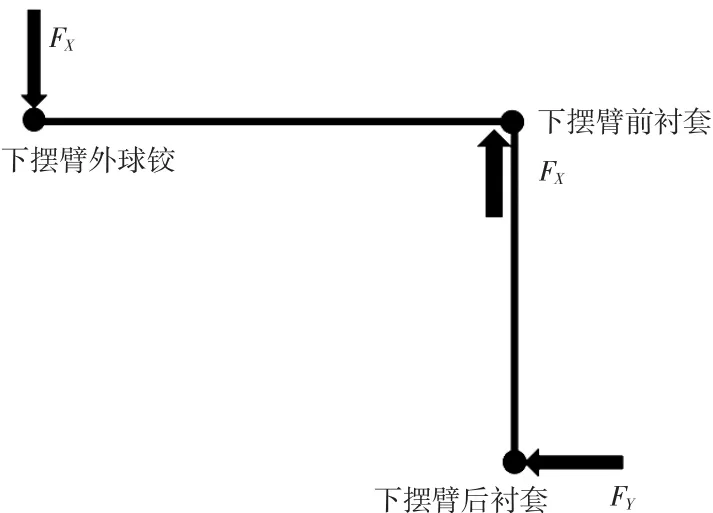
图11 下摆臂后衬套影响轴节FX

图12 后悬纵臂前衬套影响轴节FX
转向节X方向受力还与动力总成有关:车轮、驱动轴、离合器、飞轮、曲轴组成扭转振动系统。车轮撞上障碍物,车轮角速度的变化率影响车轮的撞击力。车轮的角速度的变化率与离合器的刚度、阻尼、发动机旋转件的转动惯量有关。
转向节Y方向的受力还与轮毂轴承的刚度有很强的关联。由上文可知,轮胎Z向的冲击力很大。冲击力产生的力矩使轮毂轴承产生不可忽略的扭转变形,对车轮外倾角变化产生影响。如果轮毂轴承的偏置距不为零,这种影响将更加显著。四轮定位参数中,前束、外倾对平直路段的转向节Y向受力的影响大于对搓板路段的影响。
2.3 模型优化
根据上文的分析,优化车辆模型:采用更加复杂的衬套模型,体现衬套的动态特性;后悬纵臂是薄板结构,柔性较大,用柔性体(有限元)建模;改进悬架模型,考虑轮毂轴承的柔性变形特性;改进动力总成模型,特别是离合器模型[10]。
模型优化后,将K&C仿真结果与试验台测试结果对比。通过K&C对比能判断悬架模型的精度是否达到要求。准确的悬架系统是整车仿真精准的前提。文章仅列出部分K&C对比结果。图13是轮心位移与载荷的关系。曲线的斜率是悬架的刚度。仿真与试验吻合程度高,缓冲块的刚度及其起作用的位置均十分准确。图14是轮心位移与外倾角的关系。外倾在轮心下跳时,仿真与试验有一定的偏差,但总的来说相关性很好。因此,KC对标表明模型的准确性高,模型能真实反映车辆的特性。
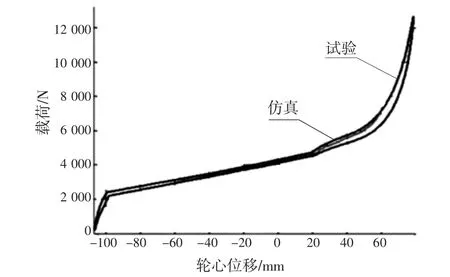
图13 轮心位移与载荷的关系

图14 轮心位移与外倾的关系
2.4 模型优化后相关性分析
模型优化后,仿真与试验的相关性对比如图15~图20所示。前悬转向节FX仿真与试验时域、频域的对比分别如图15和图16所示。FX仿真与试验时域非常接近,频域的第三个峰值仿真小于试验。频域差异的原因可能有:线性刚度、线性阻尼的离合器模型不能准确反映真实的离合器特性,即离合器的真实刚度及阻尼可能是明显的非线性特性;动刚度衬套模型不能准确反映真实的衬套特性。前悬转向节FY仿真与试验时域、频域的对比分别如图17和图18所示。FY仿真结果时域及频域均明显小于试验值。差异的具体原因有待进一步研究。前转向节FZ及后转向节FX、FY、FZ三个方向的受力,仿真结果与试验均能达到很好的吻合效果,如图19和图20所示。
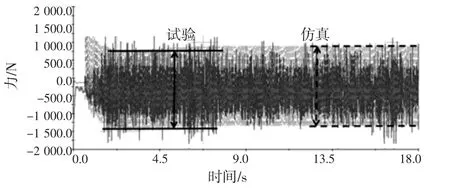
图15 前悬转向节FX时域对比

图16 前悬转向节FX频域对比

图17 前悬转向节FY时域对比
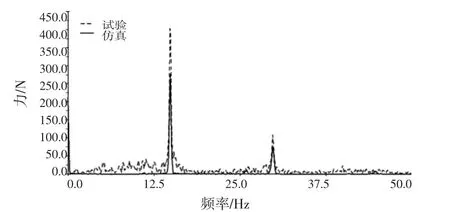
图18 前悬转向节FY频域对比
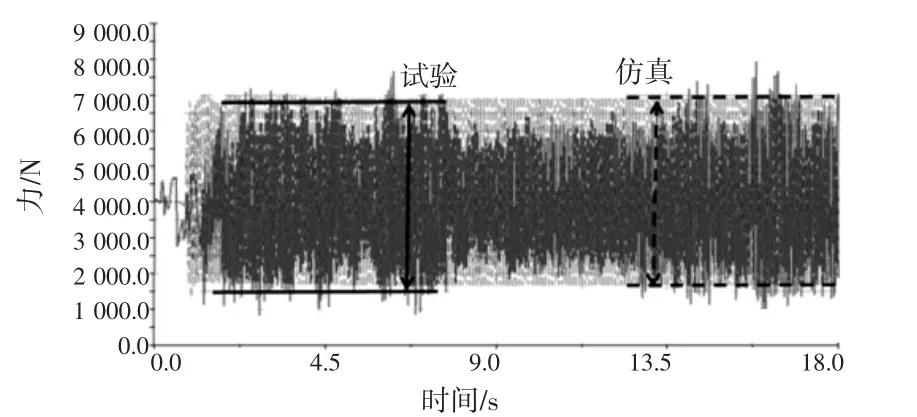
图19 后悬转向节FZ时域对比

图20 后悬转向节FZ频域对比
3 结束语
本文研究影响过搓板路仿真与试验的相关性的因素。然后根据研究结果改进模型,最终仿真结果与试验在时域和频域均高度吻合(前悬FY相关性较一般)。这表明模型准确、可信,可用于整车其他性能分析。
[1]DAS S,RAMAMURTHY P,MAHAJAN S K.Correlation issues for testing and simulation of kinematics and compliance in automotive suspensions[J].Brain Research,2007,1286(3):94-105.
[2]吴丽顺.麦弗逊悬架建模仿真以及整车的操纵稳定性分析[D].沈阳:东北大学,2010.
[3]孙琳.麦弗逊独立悬架的建模仿真与优化[D].青岛:青岛理工大学,2012.
[4]GIPSER M.FTire-the tire simulation model for all applications related to vehicle dynamics[J].Vehicle System Dynamics,2007,45(sup1):139-151.
[5]费瑞萍.FTire轮胎模型的仿真分析及试验研究[J].长春:吉林大学,2011.
[6]倪振华.振动力学[M].西安:西安交通大学出版社,1989.
[7]MOUSSEAU C W.Vehicle dynamics simulations with coupled multibody and finite element models[J].Finite Elements in Analysis and Design,1999,31(4):295-315.
[8]耶森赖姆佩尔.悬架元件及底盘力学[M].王瑄译.长春:吉林科学技术出版社,1992.
[9]SEDLACZEK K,DRONKA S,RAUH J.Advanced modular modelling of rubber bushings for vehicle simulations[J].Vehicle System Dynamics,2011,49(5):741-759.
[10]赵志强.湿式双离合器自动变速器建模及仿真分析[D].长沙:湖南大学,2009.
Analysis of Main Factors Between Test and Simulation Differences Running on Washboard Road
Yen Jinwen,Yang Man,Duan Shouyan
(Automobile Engineering Institute,Guangzhou Automobile Group Co.,Ltd,Guangzhou 510640,China)
This paper compares differences between simulated knuckle force with tested knuckle force in both time domain and frequency domain.Based on test data,it analyzes main factors that affect simulation accuracy,such as rubber elasticity,rubber damping,powertrain system,damper damping,suspension KC characteristics and so on.At last,it improves the vehicle model,and simulates analysis.The simulation result fits very well with the test data.This shows that the model is accurate and credible.
washboard road;frequency domain;time domain;rubber stiffness;damping;ADAMS
U467.1+4
A
1006-3331(2017)05-0052-05
叶锦文(1987-),男,底盘工程师;主要从事底盘性能分析及平台化研究工作。
修改稿日期:2017-07-24

