基于ADAMS的横向稳定杆与吊臂两种连接结构的计算分析

王晓莲，张学博

基于ADAMS的横向稳定杆与吊臂两种连接结构的计算分析

王晓莲，张学博

（中国第一汽车股份有限公司技术中心，长春 130011）

为了分析稳定杆与吊臂的连接结构对侧倾刚度的影响，针对目前市场上常用的两种结构，利用ADAMS软件对其进行建模和仿真。结合理论计算和台架试验结果，分析两种不同连接结构的稳定杆侧倾刚度的差异性，以及衬套和球头销等元件对稳定杆侧倾刚度的影响。

横向稳定杆；吊臂；连接结构；ADAMS

横向稳定杆是防止汽车在转弯时发生过大的横向侧倾，保持汽车平衡的悬架系统重要零件，可提高车辆的操纵稳定性，提升舒适性和安全性[1-2]。横向稳定杆与吊臂的连接形式多种多样，各有优缺点，侧倾刚度也不尽相同。本文主要研究目前市场上使用较多、性能较好的两种横向稳定杆与吊臂的连接结构，与实车参数相结合，探寻不同的稳定杆与吊臂连接结构对侧倾稳定性的影响，并利用仿真分析及台架试验进行验证，拓展开发设计的新思路。

1 两种连接结构及侧倾刚度理论计算

两种横向稳定杆与吊臂连接结构如图1所示。

图1 横向稳定杆与吊臂连接结构

对称-橡胶衬套连接结构A和悬臂-球头销连接结构B如图2所示。

图2 橡胶衬套和球头销结构

两种连接结构的横向稳定杆的应用情况如表1所示。

表 1 两种连接结构的稳定杆应用情况

图1所示的直角形横向稳定杆侧倾刚度的计算公式为[3-5]：

式中：Cφ为横向稳定杆侧倾角刚度，N·mm/rad；K为横向稳定杆单侧线刚度，N/mm；L为稳定杆横向跨度距离，mm；P为弯矩；U为扭矩；E为拉压弹性模量，E=2.06×105N/mm2；G为剪切弹性模量，G=8×104N/mm2；Ip=2×I，I=πd4/64，mm4。

如图1（a）所示，结构A稳定杆与吊臂连接形式为对称结构，其理论计算简图如图3（a）所示，根据能量原理，推导出式（1）中的P和U如下：

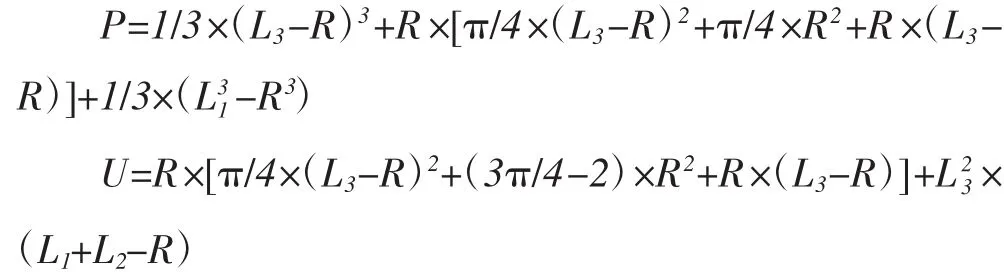
图 3 两种稳定杆与吊臂连接结构示意图

如图1（b）所示，结构B稳定杆与吊臂连接形式为悬臂结构，其理论计算简图如图3（b）所示，根据能量原理，推导出式（1）中的P和U如下：

结构A与结构B的主要区别是结构A作用力F的作用点在稳定杆端头处，结构B作用力F的作用点与稳定杆端头的距离为L4。因此，两种结构推导出的P和U存在差异。

利用式（1），计算结构A和结构B的稳定杆侧倾刚度值。在同样尺寸参数条件下，稳定杆侧倾刚度理论计算值如表2所示。

表 2 稳定杆侧倾刚度理论计算表

由上述初步计算可知，同样尺寸参数条件下，结构B比结构A横向稳定杆侧倾刚度偏大7.5%。

上述理论计算方法虽然简便易行，但却存在以下缺点[6]：仅是对横向稳定杆本身的刚度进行计算，并未考虑橡胶衬套、球头销等元件对侧倾刚度的影响，也未考虑吊臂与稳定杆的连接形式对侧倾刚度的影响；理论计算模型仅考虑稳定杆自身尺寸参数，与实车稳定杆使用工况存在一定的偏差。

2 基于ADAMS的侧倾刚度计算及台架试验

为了提高准确度，考虑稳定杆与吊臂连接结构对侧倾刚度的影响，同时增加衬套和球头销等元件，利用ADAMS软件，建立稳定杆与吊臂的多体动力学仿真模型，更能贴近台架试验和实际工况。

2.1 ADAMS建模理论

2.1.1 无质量梁

基于ADAMS软件，横向稳定杆有3种建模方法，分别为基于材料力学特性的多刚体建模方法、基于模态叠加的多柔体建模方法和基于铁木辛柯理论的多柔体建模方法[7-10]。3种建模方法各有优、缺点，在尺寸确定的情况下，基于铁木辛柯理论的建模方法求解精度高，适合稳定杆开发设计时使用。本文即采用该种方法，将横向稳定杆离散成多段刚体，刚体之间通过无质量的铁木辛柯梁[6,11]连接，如图4所示。

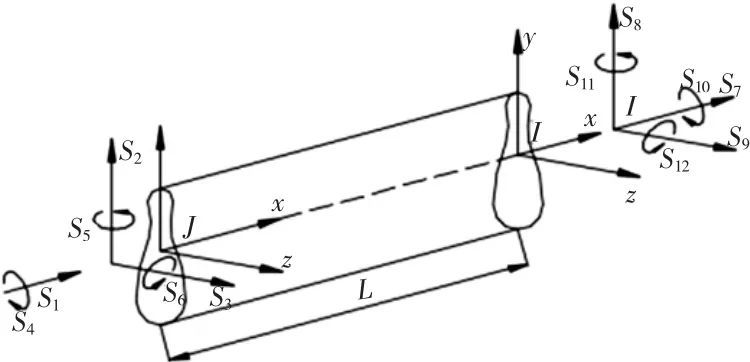
图4 无质量梁

图4 中，S1、S7为轴向力；S5、S6、S11、S12为y轴和z轴方向的转矩；S4、S10为x轴方向的转矩；S2、S3、S8、S9为剪切力。

无质量梁在梁的两端点间产生拉压力和扭转力矩，为等截面梁。在施加无质量梁时，ADAMS在梁的两个端点创建两个标记点，无质量梁产生的力和力矩的大小和梁端点处两标记点之间的相对位移和速度有关。

2.1.2 衬套力

在上述创建的横向稳定杆模型的基础上，定义衬套力或球铰约束。衬套力是两构件相互作用的弹簧和阻尼力，通过定义6个力和力矩分量，在两构件间施加柔性力和力矩，力是移动位移和速度的线性函数，力矩是转动位移和速度的线性函数，具体公式如下：

式中：[F]=[Fx，Fy，Fz，Tx，Ty，Tz]T为x、y、z轴方向的力分量和力矩分量；[L]=[x,y,z,a,b,c]T为x、y、z轴方向I、J标记点之间的相对移动位移和相对转动位移；[K]和[C]为刚度系数矩阵和阻尼系数矩阵；[V]=[Vx，Vy，Vz，ωx，ωy，ωz]T为x、y、z轴方向I、J标记点之间的相对移动速度和相对转动速度；[F0]=[F1，F2，F3，T1，T2，T3]T为x、y、z轴方向的初始力分量和初始力矩分量。

2.2 稳定杆ADAMS模型

2.2.1 仅考虑衬套Ⅰ影响的稳定杆模型

根据上述理论，仅考虑稳定杆与前轴连接的衬套Ⅰ（稳定杆与前轴连接衬套）对侧倾刚度的影响。通过33个硬点创建横向稳定杆模型，并在此基础上定义衬套力。硬点模型如图5（a）所示，结构A稳定杆的仿真模型如图5（b）所示。

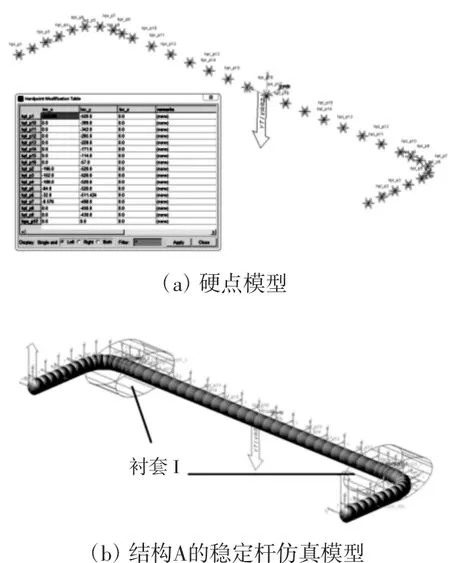
图5 稳定杆仿真模型

ADAMS创建的衬套力主要参数有3个，刚度、阻尼和预载。本文只考虑衬套刚度对横向稳定杆侧倾角刚度的影响，一般情况，衬套刚度值通过台架试验获取。仅考虑衬套影响的结构B稳定杆的ADAMS仿真模型与其类似，不再赘述。

2.2.2 综合考虑衬套和吊臂影响的稳定杆模型

在图5基础上，创建吊臂和车架模型，并根据实际工况，定义衬套或球头销。结构A和结构B的稳定杆与吊臂连接结构ADAMS仿真模型如图6所示。

图6 综合考虑衬套和吊臂影响的稳定杆与吊臂仿真模型

2.2.3 衬套径向刚度台架试验

图6（a）所示的结构A稳定杆共有3个衬套，分别为稳定杆与前轴连接衬套Ⅰ、稳定杆与吊臂连接衬套Ⅱ和吊臂与车架连接衬套Ⅲ。如图6（b）所示的结构B稳定杆共有一个衬套，与结构A中的衬套Ⅰ相同。为了便于对比分析，结构B的衬套Ⅰ取值与结构A相同。3种衬套试验测得的径向刚度值如表3所示。

表3 稳定杆衬套径向刚度试验结果 N/mm

2.3 仿真结果及分析

由式（1）可知，在稳定杆横向跨度L数值一定的情况下，侧倾刚度Cφ与单侧线刚度K成正比，因此，本文通过稳定杆单侧线刚度仿真曲线进行分析。

2.3.1 仅考虑衬套Ⅰ的影响

结构A和结构B两种吊臂结构的稳定杆，在仅考虑与前轴连接衬套Ⅰ的情况下（图5（b）），稳定杆单侧线刚度仿真曲线如图7所示。当衬套刚度变化时，稳定杆单侧线刚度随之变化，如表4所示。

图7 稳定杆单侧线刚度仿真曲线（K衬套=5 000 N/mm）

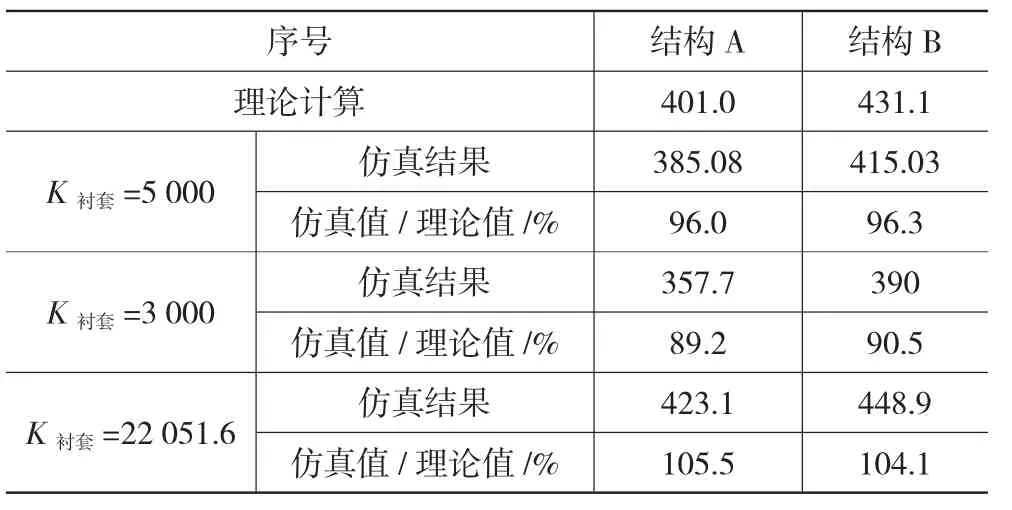
表4 稳定杆单侧线刚度对比表 N/mm

由图7和表4可以看出，当衬套Ⅰ刚度较小时，考虑了衬套Ⅰ的影响的仿真结果比理论值有所下降。当稳定杆与前轴连接衬套Ⅰ的刚度达到一定数值时，稳定杆的单侧线刚度便会比理论计算值大。当衬套Ⅰ的径向刚度达到一定数值时，结构A和结构B两种稳定杆的刚度的仿真值差异在缩小。

衬套Ⅰ刚度对于稳定杆刚度有影响，当衬套Ⅰ刚度减小或增大，稳定杆刚度也随之减小或增大。仅考虑衬套Ⅰ影响的结构B比结构A的稳定杆单侧线刚度偏高。

2.3.2 综合考虑衬套和吊臂的影响

A和B两种吊臂结构的稳定杆，在综合考虑衬套和吊臂影响的情况下，根据表3提供的稳定杆衬套径向刚度台架试验数据，稳定杆单侧线刚度仿真拟合曲线如图8所示。稳定杆单侧线刚度仿真结果：结构A为382.6 N/mm，结构B为413.0 N/mm，仿真值与理论值之比分别为95.4%和95.8%。

图8 稳定杆单侧线刚度仿真曲线

因此，综合考虑衬套和吊臂影响的稳定杆单侧线刚度仿真结果与只考虑稳定杆自身尺寸参数的理论计算结果接近度很高；当衬套刚度采用台架试验值时，综合考虑衬套和吊臂影响的结构B比结构A的稳定杆单侧线刚度偏高7.9%。

2.4 台架试验验证

对结构A和结构B的横向稳定杆及吊臂总成进行台架试验，如图9所示，测得两种结构稳定杆及吊臂总成的线刚度的拟合曲线如图10所示。

图9 结构B稳定杆台架试验

图10 稳定杆总成线刚度台架试验曲线

由图10可知，试验结果为稳定杆总成线刚度，根据式（1），将其转化为稳定杆单侧线刚度值为：结构A为387.2 N/mm，结构B为415.8 N/mm，台架试验值与理论值之比分别为96.6%和96.5%。

因此，综合考虑衬套及吊臂影响的稳定杆台架试验结果，与仅考虑稳定杆自身尺寸参数的理论计算结果非常接近。当衬套刚度较大时，台架试验结果、理论计算结果与仿真结果接近程度更大，从台架试验结果来看，结构B的稳定杆单侧线刚度依然比结构A偏大8.2%。

3 结论

1）稳定杆与吊臂连接结构对稳定杆侧倾刚度存在影响，结构B（悬臂-球头销）比结构A（对称-衬套）的稳定杆侧倾刚度偏大约6%～9%。

2）衬套刚度对稳定杆刚度影响较大，可以通过控制衬套刚度的大小调整稳定杆及吊臂总成的侧倾刚度，并且稳定杆刚度随衬套刚度的增大而增大。

3）当衬套刚度较大时，简单的理论计算与仿真和台架试验结果接近度非常大，加之其计算方法简单易行，可以在稳定杆开发设计初期阶段使用。

[1]曾林.车用稳定杆及其发展前景[J].弹簧工程，1993（2）:2-8.

[2]黄康，仰荣德.基于ANSYS的汽车横向稳定杆疲劳分析[J].机械设计,2008,25（12）:66-68.

[3]刘惟信.汽车设计[M].北京：清华大学出版社,2001.

[4]日本自动车技术会·汽车工程手册5：底盘设计篇 [M].中国汽车工程学会，译.北京：北京理工大学出版社,2010：31-33.

[5]丁能根,张宏兵,冉晓凤,等.横向稳定杆性能计算及其影响因素分析[J].汽车技术,2007（2）:19-22.

[6]李志魁,吴晓涛.考虑衬套影响的横向稳定杆侧倾刚度计算方法及其应用[J].汽车技术,2016（4）:13-16.

[7]宋健,邢如飞.带橡胶套的稳定杆有限元分析[J].汽车工程,2005,27（5）:592-594.

[8]刘一夫,朱茂桃,陈阳,等.横向稳定杆对整车侧倾及纵倾特性的影响[J].机械设计,2013,30（2）:92-96.

[9]周栋,黄虎,刘新田,等.大客车横向稳定杆有限元分析[J].上海工程技术大学学报,2008,22（3）:215-217.

[10]廖芳,王承.横向稳定杆建模方法研究[J].汽车技术,2006（7）:5-8.

[11]刘晋霞,胡仁喜,康士廷.ADAMS2012虚拟样机从入门到精通[M].北京：机械工业出版社,2013.

Calculating Analysis of Two Kinds of the Connecting Structure Between Stabilizer Bar and Hang Arm Based on ADAMS

Wang Xiaolian,Zhang Xuebo
(R&D Center,China FAW Co.,Ltd,Changchun 130011,China)

In order to analyze the influence of connecting structure on the roll stiffness between stabilizer bar and hang arm,the authors aim at two kinds of the connecting structure which are common in the present market,and use ADAMS software to build the model and make the simulation.Combining the theoretical calculation and the bench test results,they analyze the differences of the roll stiffness of the stabilizer bar with two kinds of the connecting structure,and the effect of the bushing and ball stud on the roll stiffness of the stabilizer bar.

stabilizer bar;hang arm;connecting structure;ADAMS

U463.33

A

1006-3331（2017）05-0001-04

王晓莲（1984-），女，硕士；工程师；主要从事悬架系统设计、精益化设计与开发和可靠性研究工作。

修改稿日期:2017-04-25