客车转向传动系统力矩波动的改进设计

王 用

客车转向传动系统力矩波动的改进设计

王 用

（桂林大宇客车有限公司，广西 桂林 541003）

阐述客车转向传动系统的结构型式和转向力矩波动原理，介绍转向系统硬点参数和传动轴相位角的设计原则，依据此原则对某车型转向传动系统进行改进设计并通过试验验证。

客车转向；传动系统；力矩波动；改进设计

客车转向传动系统是用来保持或改变客车行驶方向的操纵机构，由方向盘、转向轴系和转向器组成。理想的转向传动系统能将方向盘端输入的转动无损耗并等速地传递给转向器，而实现这种理想状态的最佳方案就是整个传动系轴线是一条直线。但驾驶舱内附件众多致使布置空间紧凑，这一理想状态基本无法实现，因此，目前客车转向轴系通常由不在同一直线上的转向上轴、中间轴和转向下轴分段式组成。由于十字轴万向节回转方向松动少、摩擦损失小、适合批量生产，在万向节叉与传动轴之间用花键连接时，可以利用它们之间轴向伸缩的特点弥补制造和安装误差[1]，所以，客车现普遍采用双十字轴万向节将转向中间轴分别与转向上轴和转向下轴连接。由于十字轴万向节存在不等速性，在转向操作过程中很可能出现转向力矩波动的情况，而时轻时重的转向手感将影响驾驶操纵的舒适性和安全性[2]，因此，在转向传动系统设计中必须考虑如何减少转向力矩的波动。

1 转向力矩波动分析

1.1 力矩波动因素

对于双十字轴万向节如忽略传动摩擦，其转矩有如下关系[3]：

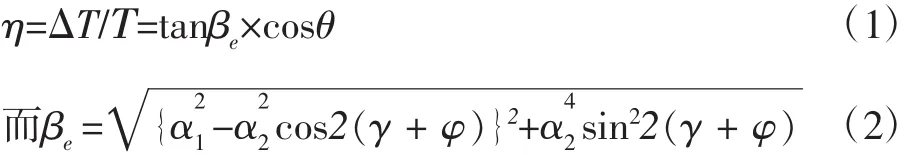
式中：η为转矩波动率；ΔT为转矩波动值；T为转向上轴输入转矩；θ为转向上轴L1的旋转角度；βe为传动轴系当量夹角；传动角α1为转向中间轴L2与转向上轴L1的夹角；α2为转向中间轴L2与转向下轴L3的夹角；γ为传动面夹角，即转向上轴L1和中间轴L2组成的平面ABC与中间轴L2和转向下轴L3组成的平面BCD之间的夹角；φ为转向中间轴轴叉相位角，即中间轴上轴叉所在平面Ⅱ和下轴叉所在平面Ⅲ之间的夹角[4]，从上往下看，平面Ⅱ到平面Ⅲ，沿顺时针为正。如图1所示，图中转向传动系统硬点A为方向盘中心；硬点B为上铰接中心；硬点C为下铰接中心；硬点D为转向器中心。

从式（1）可以看出，传动角α1及α2、传动面夹角γ和相位角φ是转向传动系统产生力矩波动的主要因素。为实现力矩无波动传动，需满足α1=α2且γ=φ=0或α1=α2且γ=-φ[5]。由于客车驾驶区空间有限，转向传动系统在任何操作位置上不得与其他部件有干涉现象[6]，而且方向盘需要调节位置以适应不同驾驶人群，以上条件实际难以满足。如果转向力矩波动幅度过大将影响驾驶操控，当波动率控制在5%以内时可满足驾驶要求[7]。

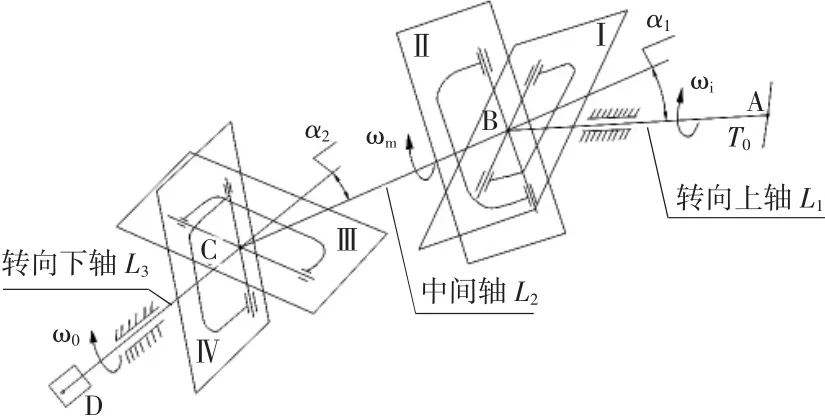
图1 双十字轴万向节传动轴布置示意图

1.2 力矩波动理论计算

对于双十字轴万向节转向传动系统，根据式（1）和式（2），按照“当量夹角越小，传动性能越好”的原则进行设计[8]。即在设计前期，根据总体布置的驾驶区空间及人机工程学初步选取方向盘的设计位置及调节范围，再综合驾驶区其他零件的布置情况优化转向系统中各硬点的坐标，并选取合适的转向中间轴轴叉相位角使方向盘在各个位置时转向系统的力矩波动满足驾驶要求[9]。

方向盘处于任一位置时，转向系统硬点A的坐标表示为（XA，YA，ZA），B的坐标为（XB，YB，ZB），C的坐标为（XC，YC，ZC），D的坐标为（XD，YD，ZD）。

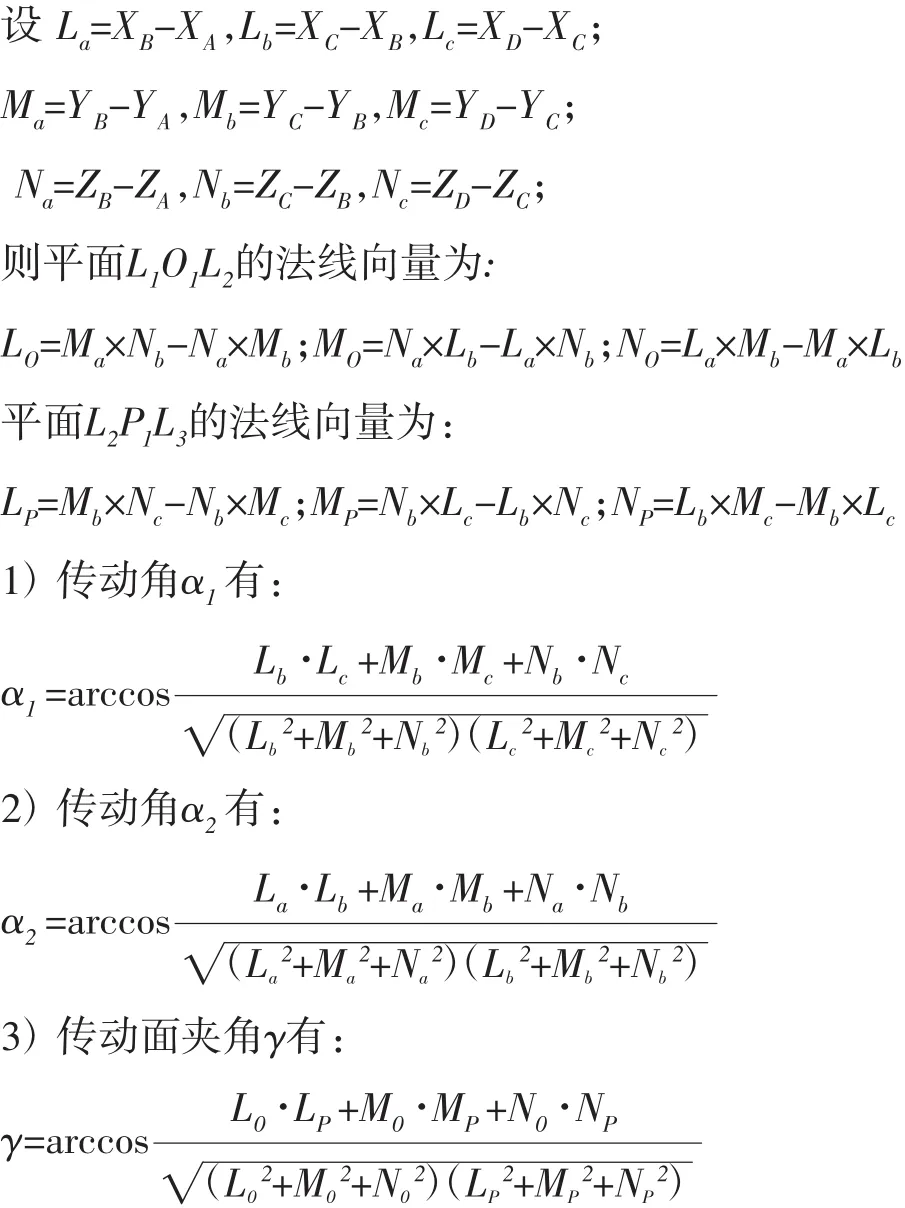
由以上各式可计算出α1、α2和γ。为获得最佳传动性能，βe应尽可能小，取φ=-γ或φ=π-γ时，βe有最小值为，而力矩波动率是随转向上轴转角变动的周期函数，当cosθ=1时有最大值，如波动率合格，则转向传动系统硬点坐标和相位角的选取方案可行。

2 转向力矩波动改进设计

2.1 转向传动系统布置改进

根据车辆转向传动系统布置图，对转向传动系统数模进行测算得到α1、α2和γ的数值如表1中的改进前部分，根据当量夹角最小，传动性能越好的设计原则，应当取最佳相位角φ=-γ，实际圆整后取φ=-19°，由于传动轴夹角α1和α2差值较大，计算得η=7.1%，不能满足要求。

表1 转向系统改进前/后数据

为降低转向力矩波动，在驾驶区空间允许范围内，调整转向传动系统硬点A、B、C、D的坐标参数，将方向盘和转向上轴安装倾角增加2°，再重新布置转向器和转向下轴，数模测算结果如表1中的改进后部分，圆整后取最佳相位角φ=-11°时转向力矩波动率η=1.6%，理论上可满足使用要求。

2.2 实测分析与验证

忽略万向节摩擦损失，对于双十字轴万向节输入轴（转向上轴）转矩T1和输出轴（转向下轴）转矩T2及各自旋

上式中i为双十字轴万向节瞬时传动比，其数值大小反映了转向力矩波动的大小。

当车辆怠速原地保持恒定转速转动方向盘时，因发动机转速和转向杆系传动比均保持不变，则T2也可认为是恒定值。依据式（3）得T1max/T1min=imax/imin，而方向盘直径尺寸不变，则车辆转动方向盘所需转向力反映了转向力矩的大小。所以，转向力最大值与最小值的比值也反映了转向力矩的波动率的大小，比值越接近1，则转向力矩的波动率越小。

按改进前和改进后状态分别将φ=-19°和φ=-11°两件不同相位角的转向传动轴装配于同一样车进行转向力实测，试验车辆方向盘匀速从左极限转到右极限位置约4圈，取第2和第3圈的转向力数据及最大与最小的比值进行分析比较，测试结果如表2所示。

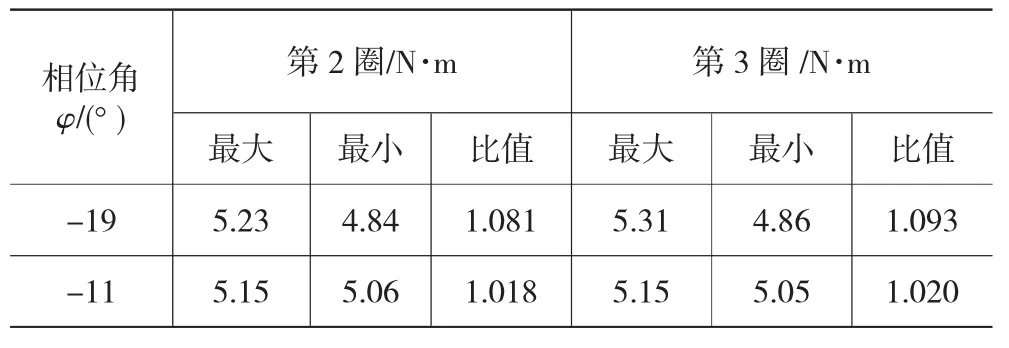
表2 转向力矩测量值T1

从试验数据可看出，转向传动轴相位角φ=-11°状态安装的方向盘转向力最大值与最小值的比值明显比相位角φ=-19°时的比值小，相应的其转向力矩波动也小（η=1.6%），试验结论与模拟计算基本一致，车辆转向传动系统设计改进方案可行。

3 结束语

方向盘力是汽车操纵稳定性评价的重要指标[10]。车辆转向传动系统按照“当量夹角越小，传动性能越好”的原则进行设计改进，并经过转向力对比测试验证，实测结果与理论计算一致，确保了车辆转向传动系统满足使用要求。

[1]汽车工程手册编辑委员会.汽车工程手册:设计篇[K].北京:人民交通出版社,2001.

[2]陈家瑞.汽车构造:下册[M].3版.北京:人民交通出版社，1997.

[3]王霄锋.汽车底盘设计[M].北京:清华大学出版社，2010.

[4]冯帆，刘优.汽车转向传动轴相位角的设计[J].企业技术开发：下旬刊,2016（2）：6-7.

[5]潘宇，何云峰，何志兵，等.双十字轴万向节转向传动系统的优化设计[J].机械传动，2015（1）：83-86.

[6]公安部道路交通管理标准化技术委员会.机动车运行安全技术条件:GB 7258-2012[S].北京：中国标准出版社，2012：9.

[7]王斌.转向力矩波动的校核方法[J].时代农机，,2015（4）：27-28.

[8]裴锦华，李明.汽车转向系统力矩波动的匹配研究[J].汽车科技,2010（3）：48-51.

[9]刘惟信.汽车设计[M].北京:清华大学出版社,2001.

[10]余志生.汽车理论[M].北京:机械工业出版社,2000.

Improvement Design of Torque Fluctuation for Bus Steering Transmission System

Wang Yong
(Guilin Daewoo Bus Co.,Ltd,Guilin 541003,China)

The authors elaborate the structure style and torque fluctuation theory of bus steering transmission system,introduce the design principles of hard points parameters and transmission phase angle of steering system.According to these principles,they improve the design of the steering transmission system of this vehicle,and verify the results through testing.

bus steering;transmission system;torque fluctuation;improvement design

U463.4

B

1006-3331（2017）05-0023-03

王 用（1981-），男，工程师；主要从事客车底盘设计和研究工作。

修改稿日期:2017-05-18