基于全局方差和噪声估计的维纳滤波图像的复原方法
李东升,陈春晓,王章立,杨俊豪
(南京航空航天大学生物医学工程系,南京 211106)
1 引 言
图像复原是利用图像处理的知识,从降质图像恢复得到接近真实图像的方法。图像复原的优劣在一定程度上影响后续图像的处理和分析[1]。因此,图像复原在医学影像、天文观测、刑事侦查等领域有广泛的应用。
常用的图像复原方法有维纳滤波、最小二乘法、最大似然估计等。其中维纳滤波器是基于最小均方差准则的复原方法,可以使逆滤波和噪声平滑过程中的均方差最小化,适用于抑制加性或乘性噪声[2]。维纳滤波将退化图像与噪声统计特性一并纳入复原过程,因而可以在消除加性噪声的同时恢复模糊图像[3]。作为一种经典的复原算法,维纳滤波也在不断地被改进。Lahmiri等提出了混合维纳和偏微分方程滤波方法,在图像复原中取得了良好的结果[4];Aouinti等将遗传算法应用到迭代维纳滤波器中,提出了可迭代的维纳滤波方法[5];张红民、陈新平等使用局部方差替代维纳滤波中固定的K值,提出了自适应变参数维纳滤波方法[6-7];刘晓辉等使用噪声方差代替维纳滤波中的噪声功率,对退化图像进行二次维纳滤波,获得了较好的处理效果[8]。然而以上算法仍存在不稳定、易失真的问题,本研究提出了基于全局方差和误差估计的维纳滤波方法。实验证明,该方法可以保持图像复原过程的稳定性,通过设置合适的修正参数可以获得较高质量的复原结果。
2 维纳滤波
图像在传输过程中受到噪声等因素的干扰,会导致图像退化失真,图像退化过程可表示为:

其中,f表示未退化的清晰图像,h表示观测系统的点扩散函数,n表示图像获取过程中的噪声,g为降质退化图像。图像复原即根据已知条件通过一定方法获得未退化清晰图像。将公式(1)变换到频域,图像退化模型转化为:
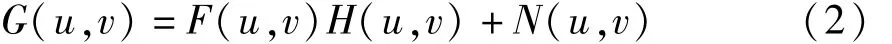
其中 G(u,v)、F(u,v)、H(u,v)、N(u,v)分别为g(x,y)、f(x,y)、h(x,y)、n(x,y)的傅里叶变换。若忽略噪声的影响,可进一步得到:
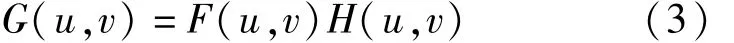
因此,通过构造一个理想的滤波器W(u,v)与已知的退化图像频谱G(u,v)点乘,可以得到理想的原图像频谱F(u,v),进而恢复原图像:

然而,由于使图像模糊的系统点扩散函数往往是一个低通滤波器,其在高频部分的值很小,甚至接近于零,造成其倒数在高频部分的值过大,这种逆滤波器会过分放大图像的细节,容易造成复原结果失真[1],不能有效地复原图像。为解决这一问题,工程上常在公式(4)的分母上加入一个合适的正则项r,则滤波器的表达式可以写成:
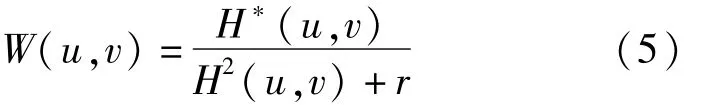
其中,H*(u,v)是 H(u,v)的共轭。对于公式(5),当H较大时,正则项r几乎不起作用,滤波器近似于理想的逆滤波器;当H较小时,由于r的存在滤波器对高频部分过分放大的作用将会受到抑制,保证复原结果不会失真。
维纳滤波的目的是使原始清晰图像f(x,y)与复原得到的估计图像(x,y)之间的均方差最小,即满足:
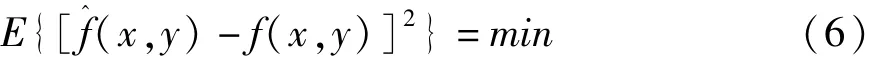
其中E[·]代表数学期望算子。求解方程(6),可得:

其中 Pn(u,v)为噪声功率,Pf(u,v)为原始清晰图像功率。W(u,v)即为维纳滤波器的传递函数。然而在实际工程中,原始清晰图像和噪声类型往往未知,因此常使用公式(8)来近似维纳滤波器的传递函数:
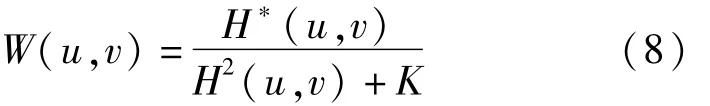
其中K是一个合适大小的常数。对于不同图像,常数K的选取需要根据实验决定,不能够充分利用图像信息,难以得到理想的复原结果,这种方法通常只适合在图像要求不高的情况下使用[9]。针对该问题,可以使用频域矩阵K(u,v)或空域矩阵K(x,y)来代替常数K,以获得自适应的参数,代替固定的 K值[10]。
因此,如何利用先验知识获得原始清晰图像和噪声的估计成为重要的研究内容。刘晓辉等人提出了改进的二次维纳滤波方法[8]。该方法利用公式(8)对退化图像进行第一次复原,获得原始清晰图像功率谱Pf(u,v)的近似估计,进而利用第一次维纳滤波前后两幅图像的差值得到噪声的估计。
实验表明,在高信噪比下,该方法可以获得细节丰富的图像,但低信噪比下往往会产生失真。针对上述问题,本研究提出了一种基于全局方差和噪声估计的维纳滤波新方法。
3 基于全局方差和误差估计的维纳滤波
针对文献[8]中的方法在低信噪比情况下复原效果差的问题,本研究将噪声功率谱引入维纳滤波算法,以增强算法稳定性,并结合全局方差,对维纳滤波方法进行了如下改进:
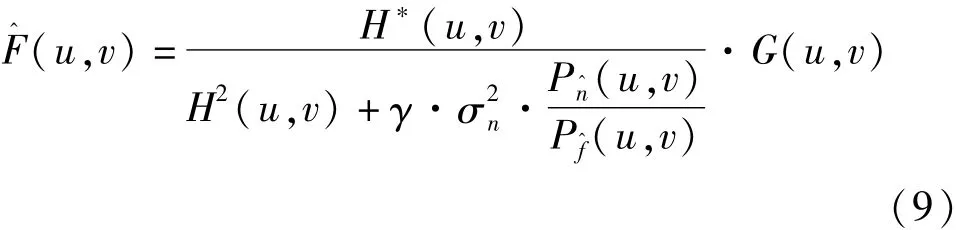
实际工程中,噪声的估计可分为基于块和滤波的两类方法[11]。本研究使用3×3的均值滤波算子对退化图像进行平滑,并将处理前后图片的差值作为噪声的估计。由于全局方差在强噪声时数值较小,不能很好地起到修正的作用。本研究引入修正参数γ来获得更好的修正能力。选取γ=min(M,N),其中M,N为图片的长度与宽度。
4 实验结果和分析
选取Lenna图像进行实验,采用模糊核尺寸为,标准差为3的高斯型点扩散函数,对图像进行模糊,并分别加入方差为 10-i,i=2,4,6,8,10的高斯型噪声。使用文献[6-7]中固定K值的维纳滤波方法(K=0.1),文献[8]提出的改进的二次维纳滤波方法,与本研究提出的方法对模糊加噪图像进行复原,复原结果见图1。

图1 模糊加噪图像及其复原结果。(a1)-(a5):噪声方差分别为10-i;i=2,4,6,8,10的模糊加噪图像,(b1)-(b5):固定 K值维纳滤波复原结果;(c1)-(c5):改进的二次维纳滤波复原结果;(d1)-(d5):本研究提出方法复原结果Fig 1 Blurred and degraded images and results of recovery.(a1)-(a5):Blurred and degraded images corrupted by noises with variances 10-i,i=2,4,6,8,10;(b1)-(b5):The recovery results of Wiener filter with fixed K;(c1)-(c5):The recovery results of improved Wiener filter;(d1)-(d5):The recovery results of method proposed in this article
为了客观地评价图像复原的质量,本研究使用三个指标对图像复原结果进行评价,即峰值信噪比(peak signal to noise ratio,PSNR),均方误差(mean square error,MSE)和结构相似性(structural similarity index,SSIM)。其中 PSNR越大、MSE越小,表示图像复原质量越好,SSIM的数值越接近1,表示两幅图像相似度越高。表1给出了各种方法进行图像复原后的性能指标。
从图1及表1可以看出,在强噪声下,本研究提出的方法明显优于固定K值和文献[8]提出的改进二次维纳滤波算法。在噪声较弱时,本研究提出的算法复原能力与文献提出的改进二维维纳滤波方法差别不大。此外,实验发现,由于噪声估计方法能力有限,随着噪声强度减弱该方法对噪声方差的估计结果最终趋于某定值。因此在弱噪声情况下,使用γ=min(M,N)作为修正参数时,如果γ数值过大,会导致复原图像质量下降,此时作为补充,可考虑使用γ=1作为修正参数,以获得较小的数值。图2给出了模糊核尺寸为10×10,标准差为3的高斯型点扩散函数模糊图像后,分别加入方差为10-i,i=2,4,6,8,10的高斯噪声的情况下,使用 γ=min(M,N)和γ=1两种方法复原图像的结果。从表2可以看出,当噪声强时,使用γ=min(M,N)作为修正参数复原结果很好,而在噪声较弱时,为获得更多的图像细节信息,取γ=1时,图像复原的质量更好。

图2 改变值图像复原结果。其中(a1)-(a5):取 γ=min(M,N),噪声方差分别为10-i,i=2,4,6,8,10图像复原的结果;(b1)-(b5):取 γ=1,噪声方差分别为10-i,i=2,4,6,8,10图像复原的结果Fig 2 The recovery results by changing the value of.(a1)-(a5):The recovery results of images corrupted by noises with variances10-i,i=2,4,6,8,10 whenγ=min(M,N);(b1)-(b5):The recovery results of images corrupted by noises with variances10-i,i=2,4,6,8,10 whenγ=1.

表1 模糊加噪图像复原结果的性能指标Table 1 The performances of recovery results of the blurred and degraded images

表2 模糊加噪图像复原结果的性能指标Table 2 The performances of recovery results of the blurred and degraded images
根据Lenna图像的复原结果及性能指标对比,可以看出,根据噪声强弱程度调整修正参数γ,算法对图像的复原能力优于固定K值的维纳滤波算法和文献中提出的二次维纳滤波算法。此外,当工程上获得的图片受噪声干扰严重时,可选用γ=min(M,N)作为修正参数对图像进行复原;而当图像受噪声干扰较弱时,可使用γ=1作为修正量对图像进行复原处理。利用本研究提出的方法对实验中获得的显微切片图像进行复原,复原结果见图3。从图3中分别利用修正参数为γ=min(M,N)和γ=1的本研究方法对显微切片图像进行复原,进一步验证,根据图像中的噪声强度调节参数γ可以更好地提高图像复原的质量,恢复图像原本的细节信息。

图3 病理切片图像复原。其中,(a1)强噪声病理切片图像,(b1)γ=min(M,N)时(a1)的复原结果,(c1)γ=1时(a1)的复原结果;(a2)弱噪声病理切片图像,(b2)γ=min(M,N)时(a2)的复原结果,(c2)γ=1时(a2)的复原结果。Fig 3 The recovery results of pathological images.(a1)Pathological section with strong noise;(b1)The recovery results of(a1)when(b1)γ=min(M,N);(a2)Pathological section with week noise;(b1)The recovery results of(a1)whenγ=1
5 结论
本研究充分利用已知图像的先验知识,结合噪声估计及全局方差,对维纳滤波的图像复原方法进行了改进。实验表明,本研究提出的算法复原质量较高,性能稳定,抗噪能力强,失真小,在图像复原方面具有一定的实用价值。

