压电陶瓷堆位置对郎之万换能器内部损耗的影响

梁召峰



压电陶瓷堆位置对郎之万换能器内部损耗的影响

梁召峰

(深圳职业技术学院，广东深圳518055)

压电陶瓷堆位置是郎之万换能器优化设计的一个重要对象，人们对其研究较多但结论并不一致。文章主要考虑压电陶瓷的机械损耗及介电损耗，分析了恒振幅输出时这两种损耗与压电陶瓷堆位置的关系，并通过引入负载系数探讨了不同负载情况下压电陶瓷堆位置对郎之万换能器内部损耗的影响。分析结果表明，对于不同的负载，压电陶瓷堆均对应一个最佳位置，此时换能器的内部损耗最小，且随着负载的增大，这一最佳位置逐渐向换能器的节点位置靠近。可见，压电陶瓷堆位置的优化设计与实际负载密切相关，以往关于该问题的不同结论源于其仅针对某种特定负载分析而得。

郎之万换能器；压电陶瓷；机械损耗；介电损耗

0 引言

在功率超声领域，郎之万换能器(即夹心式超声换能器)由于具有效率高、结构简单、易于优化等优点，得到了最为广泛的应用。当郎之万换能器各部分的材料确定后，如何优化结构使其性能最佳是实际应用中的首要问题，其中压电陶瓷堆位置是非常重要的优化设计对象，为此人们分别从理论和实验两方面做了大量的研究。Lemaster等[1]曾设计了多个压电陶瓷堆位置不同的郎之万换能器，并通过实验测量了各自的特性参数，结果表明压电陶瓷堆位置对换能器的机械品质因数、阻抗及位移等特性有很大影响。Shoh[2]认为对于大振幅工作的郎之万换能器，当压电陶瓷位于距后端/12处时，换能器的效率最高，原因是此时因电场引起的损耗和因机械应力引起的损耗相等。丁大成等人[3]对几个郎之万换能器分别以空气和水为负载进行实验，发现将压电片置于应力波节附近时电声效率会显著提高。Kielczyński等人[4]通过测量压电陶瓷位置不同的两个郎之万换能器工作时的表面温度分布，发现在相同功率下换能器表面的温升均出现在压电陶瓷堆处且近似相等，从而认为压电换能器的损耗主要来自于高电压引起的介电损耗，而由振动引起的机械损耗贡献不大。Mathieson等人[5]近期实验研究了压电陶瓷堆的位置对郎之万换能器非线性行为的影响，发现压电陶瓷堆越靠近换能器的位移节点，换能器的谐振频率漂移以及输出振幅跳变等非线性行为越显著。虽然在小信号下，通常认为压电陶瓷堆越靠近换能器位移节点，则换能器的有效机电耦合系数越高，但在大信号下，Mathieson等人的实验结果表明，此时换能器的频率以及振动稳定性最差。可见，虽然人们对于压电陶瓷堆置于何处郎之万换能器性能更佳的问题进行了很多研究，但结论并不一致，因此有必要从理论上进行分析并给予明确解释，从而指导郎之万换能器的优化设计。

1 理论基础

郎之万换能器的一般结构如图1所示。压电陶瓷在换能器中的位置用l表示，其大小代表压电陶瓷堆中心距离换能器位移节点的远近。郎之万换能器的横向尺寸通常小于其谐振频率对应的换能器材料中声波波长的1/4，因此在分析时可以用一维理论近似处理。取图1所示坐标，当郎之万换能器两端自由时，各部分的位移可表示为(省略简谐振动的时间因子ejωt)：

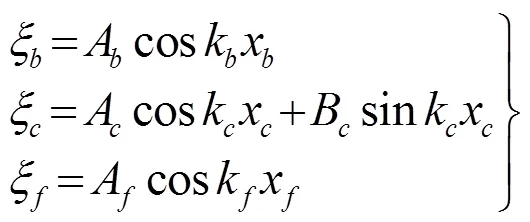
其中，、、分别为后盖板、压电陶瓷及前盖板的波数。选取型压电方程，每部分的应力分布为

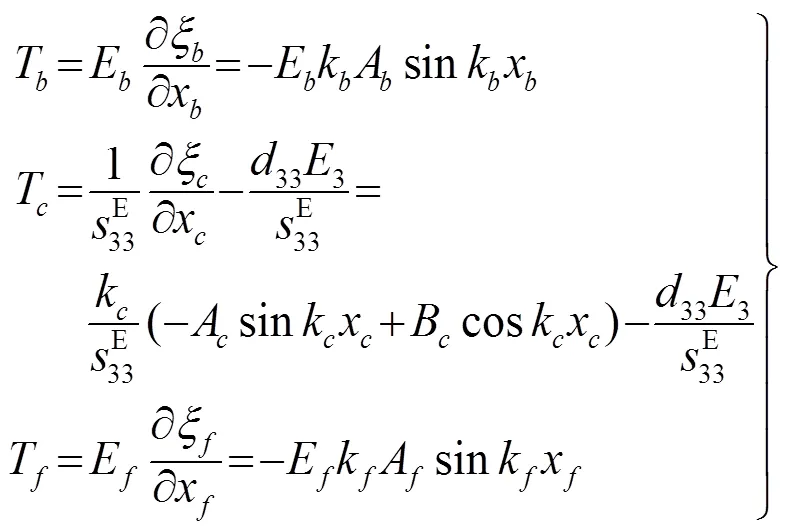
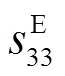
郎之万换能器的内部损耗主要包括材料的损耗以及各元件间的接触损耗。接触损耗与换能器的工艺水平密切相关，很难理论计算。对于材料损耗，由于郎之万换能器的材料主要包括金属材料及压电陶瓷，而金属材料的损耗较陶瓷材料低两个量级[6]，因此这里主要考虑压电陶瓷的损耗。

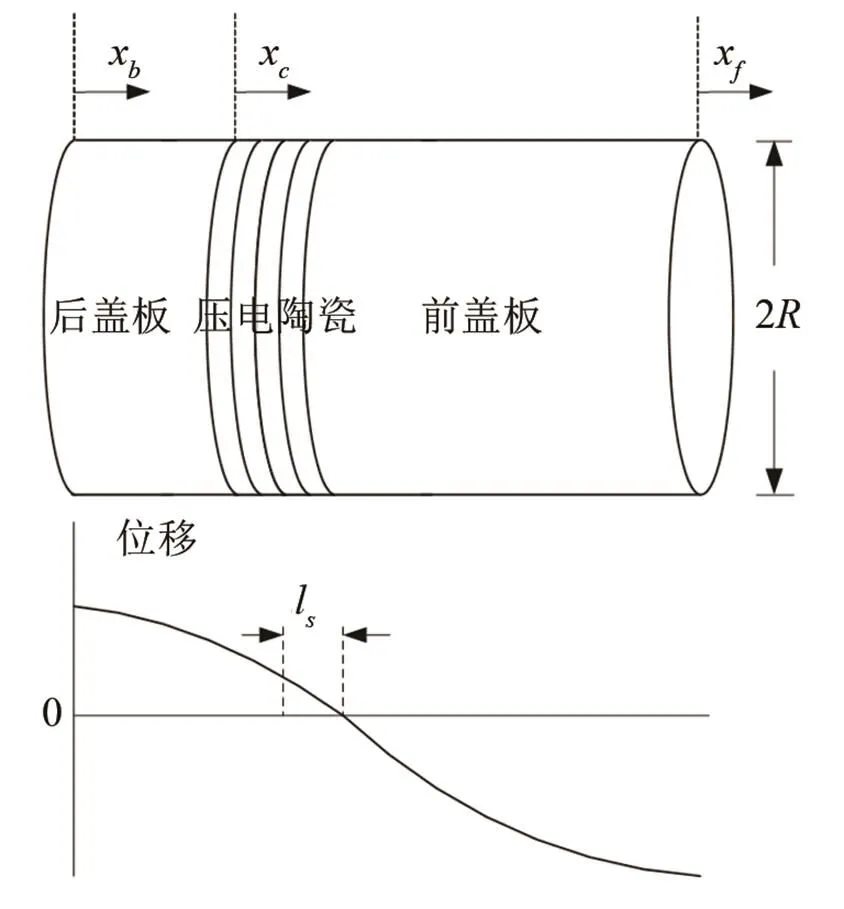
图1 郎之万换能器结构及位移分布示意图

压电陶瓷的损耗包括介电损耗、机械损耗以及压电损耗，这些损耗源于在强外电场或高应力作用下产生的电场、电位移、应力或应变之间的迟滞，从而导致压电陶瓷发热及饱和现象的出现[7]。为了表征这些损耗，人们引入了复数形式的介电、弹性及压电常数，分别将各复常数的虚部和实部之比定义为介电损耗因子tan、机械损耗因子tan及压电损耗因子tan[8-9]。介电损耗因子tan随电场的变化通常在低频下测量，因为此时其机械内应力很小；机械损耗因子tan随机械应力的变化通常在谐振频率处测量，此时所需电场很小；压电损耗因子tan由于很难测量，至今可得的实验数据非常有限。基于此，本文在分析郎之万换能器内部损耗时仅考虑由压电陶瓷材料引起的介电损耗和机械损耗。单位体积压电陶瓷的机械损耗功率及介电损耗功率可分别表示为[10]

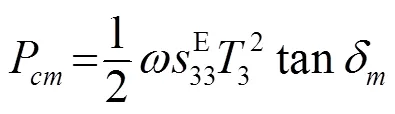
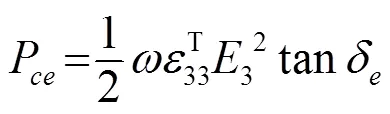
若已知换能器各部分的材料参数，联立式(1)~(2)可得在给定驱动电压下换能器的位移及应力分布曲线，或在给定输出振幅下所需的驱动电压情况，并可进一步计算获得压电陶瓷堆位置与换能器振动特性的关系。在此基础上，将式(3)~(4)沿压电陶瓷堆轴向积分并乘以面积即可得郎之万换能器的机械损耗总功率及介电损耗总功率。

2 算例及分析

计算中郎之万换能器各部分截面大小一样，直径为50 mm，前盖板为硬铝(=2.79×103kg/m3，=7.15×1010 N/m2)，后盖板为钢(=7.85×103 kg/m3，=2.05×1011 N/m2)，压电陶瓷为PZT-8，厚度为5 mm，33=2.18×10-10C/N，=8.85×10-9F/m，=1.39×10-11 m2/ N，tan=0.005，tan=0.01。取换能器谐振频率为20 kHz，输出振幅为1 μm，压电陶瓷取2片。结合工程实际，计算中压电陶瓷堆从换能器中部位置依次向后盖板方向移动。移动时钢后盖板在缩小，硬铝前盖板在加长。图2给出了压电陶瓷堆在移动过程中分别位于三个不同位置(即不同)时所对应的换能器尺寸。

图2 三个不同ls值所对应的郎之万换能器尺寸

由于计算过程中换能器处于空载状态，在谐振时计算出的电场值非常小，这里将电学量计算结果用相对值表示。图3给出了压电陶瓷堆处于不同位置时，为保证郎之万换能器恒振幅(1μm)输出，需在换能器电端施加电压的相对值。可见，压电陶瓷堆靠近节点时所需驱动电压最小，越偏离节点所需驱动电压越大。这一结果是容易理解的，因为压电陶瓷越靠近节点其有效机电耦合系数越大。

图4给出了郎之万换能器输出振幅为1μm时，机械损耗及相对介电损耗随压电陶瓷位置的变化情况。可见，随着压电陶瓷堆偏离节点位置，机械损耗逐渐变小，但介电损耗逐渐增大。压电陶瓷堆在节点处时，机械损耗最大，介电损耗最小。

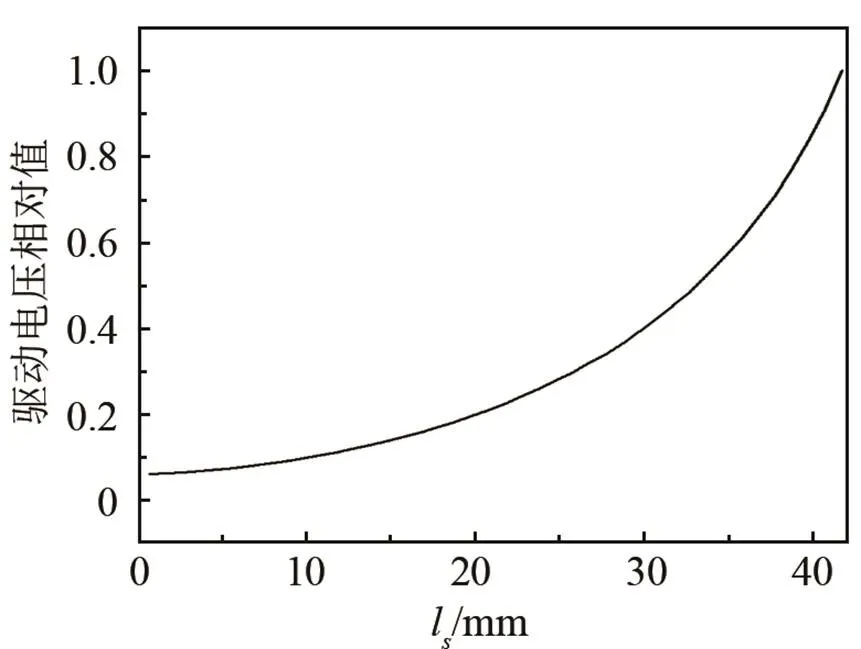
图3 恒振幅输出时所需的驱动电压与压电陶瓷堆位置的关系

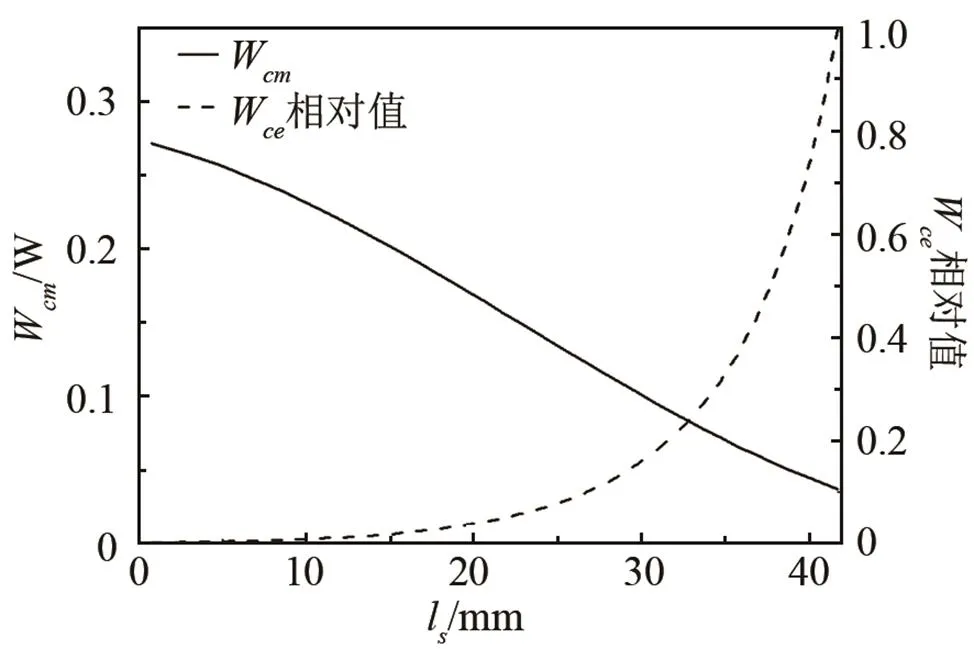
图4 恒振幅输出时机械损耗及相对介电损耗与压电陶瓷堆位置的关系

郎之万换能器的内部总损耗为机械损耗和介电损耗之和，其大小与换能器的振幅以及负载情况有关。负载会影响换能器的谐振频率，同时对于不同的负载，要保证恒振幅输出，输入电压变化很大，因而介电损耗受负载的影响很大。考虑换能器都在谐振频率上工作，其振动模态相同，在输出振幅不变的情况下，可近似认为换能器的机械损耗不变[11]。这样，郎之万换能器的内部损耗可近似表示为

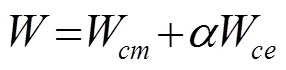
由图5可见，随着负载的增大，换能器的内部损耗也增大；对于不同的负载，压电陶瓷堆均有一个最佳位置，此时换能器的内部损耗最小，而且随着负载的增大，这一最佳位置逐渐向节点位置靠近。因此，当材料参数确定时，压电陶瓷堆的最佳位置由具体工作条件即负载情况决定。

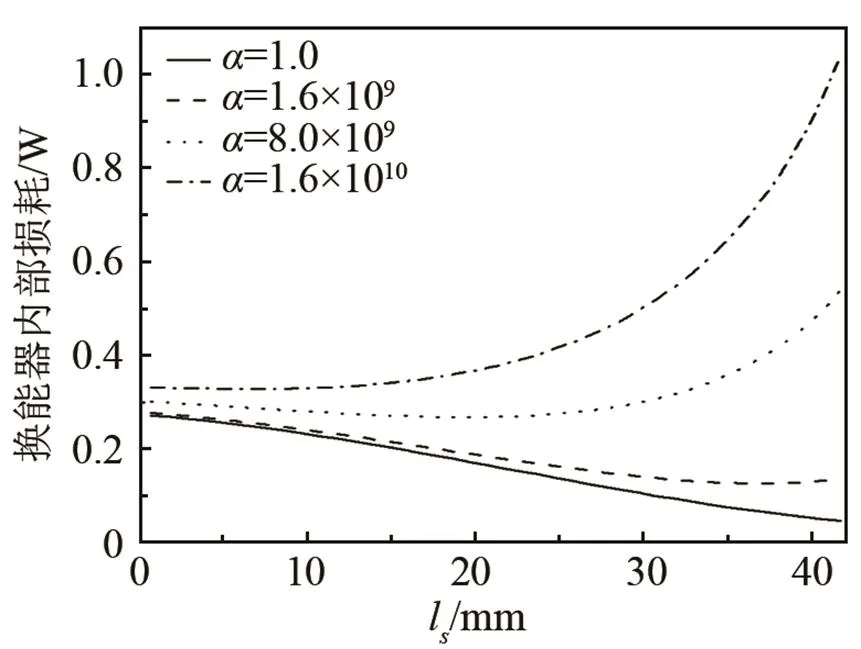
图5 不同负载时郎之万换能器内部损耗与压电陶瓷堆位置的关系

3 结论

国内外学者对于郎之万换能器中压电陶瓷堆位置的优化问题进行了比较深入的研究，但大多数研究仅限于某个特定负载情况因而所得结果各异。本文基于现有的压电陶瓷研究基础，分析了压电陶瓷堆位置对郎之万换能器的机械损耗及介电损耗的影响，通过引入负载系数定性地研究了不同负载情况下郎之万换能器内部损耗与压电陶瓷堆位置间的关系，结果表明压电陶瓷堆的最佳位置与实际负载息息相关，且随着负载的增大最佳位置逐渐逼近换能器的节点位置。本文的研究为郎之万换能器中压电元件的位置优化提供了理论依据，也是对该问题已有分歧结果的一个简明解释。

[1] Lemaster R A, Graff K F. Influence of ceramic location on high power transducers performance[C]//IEEE Ultrasonics Symp. Proc., 1978, 296-299.

[2] Shoh A. Sonic transducer: 美国, 3524085[P]. 1970-08-11.

[3] 丁大成, 牛勇. 压电陶瓷复合振子的电声效率与振子压电片位置关系的实验研究[J]. 声学学报, 1983, 8(6): 382-385. DING Dacheng, NIU Yong. Experimental investigation of the relations between the electro-acoustical efficiency of compound piezoelectric vibrator and the positions of ceramics within the vibrator[J]. Acta Acustica, 1983, 8(6): 382-385.

[4] Kielczyński P, Pajewski W. Analysis of temperature fields in ultrasonic transducers of high power[J]. Sensors and Actuators A : Physical, 1993, 36(2):97-103.

[5] Mathieson A, Cardoni A, Cerisola N, et al. The influence of piezoceramic stack location on nonlinear behavior of Langevin transducers[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2013, 60(6): 1126-1133.

[6] 周光平, 程存弟, 鲍善惠. 夹心换能器的节点位置对其特性的影响分析[J]. 声学学报, 1992, 17(4): 308-312. ZHOU Guangping, CHENG Cundi, BAO Shanhui. An analysis concerning influence of node location on performance of sandwich transducer[J]. Acta Acustica, 1992, 17(4): 308-312.

[7] Hall D A. Review nonlinearity in piezoelectric ceramics[J]. Journal of Materials Science, 2001, 36(19): 4575-4601.

[8] Land C E, Smith G W, Westgate C R. The dependence of the small-signal parameters of ferroelectric ceramic resonators upon state of polarization[J]. IEEE Transactions on Sonics and Ultrasonics, 1964, 11(8): 118-119.

[9] Martin G E. Dielectric, piezoelectric, and elastic losses in longitudinally polarized segmented ceramic tubes[J]. U. S. Navy J Underwater Acoustics, 1965, 15(2): 329-332.

[10] Berlincourt D A. Piezoelectric and ferroelectric energy conversion[J]. IEEE Transactions on Sonics and Ultrasonics, 1968, SU15(2): 89-97.

[11] Mori E, Ueha S, Tsuda Y. Large amplitude characteristics of bolt-clamped Langevin type vibrator[C]//11th International Congress on Acoustics, 1983, 154-159.

Influence of piezoceramic stack location on internal losses of Langevin transducer

LIANG Zhao-feng

(Shenzhen Polytechnic, Shenzhen 518055, Guangdong,China)

Piezoceramic stack location is an important optimization design object of Langevin transducer, and many researches on this topic have been done but there are no consistent conclusions. In this paper, mechanical loss and dielectric loss of piezoceramic are mainly considered, and the relation between these two kinds of losses and the piezoceramic stack location is analyzed under the circumstances of constant output amplitude. Moreover, by introducing the load coefficient, the influence of the piezoceramic stack location on internal losses of Langevin transducer is discussed under different load conditions. The results show the piezoceramic stack corresponds to a best location for different loads, and at this time the internal losses of Langevin transducer is the smallest. The best location is gradually close to the displacement node of the transducer as the load increases. Thus it can be seen that the optimal design of piezoceramic stack location is closely related to the actual load, and the inconsistent conclusions about the problem by far stem from these analyses only to specific loads.

Langevin transducer; piezoceramic; mechanical loss; dielectric loss

TB559

A

1000-3630(2017)-02-0188-04

10.16300/j.cnki.1000-3630.2017.02.016

2016-08-15;

2016-11-07

国家自然科学基金(11304207)、广东省自然科学基金(S2012010010402)、深圳市基础研究项目(JC201006020762A)资助。

梁召峰(1979－), 男, 陕西凤翔人, 博士, 副研究员, 研究方向为功率超声。

梁召峰, E-mail: liangzf@szpt.edu.cn