基于模糊层次分析的空间谱估计性能评价方法
王庆,周彬
基于模糊层次分析的空间谱估计性能评价方法
王庆1,2,周彬1,2
(1. 杭州应用声学研究所,浙江杭州310023;2. 声呐技术重点实验室,浙江杭州310023)
在已经形成的多种空间谱估计方法中,为根据需求选择最优算法,建立了一种基于模糊层次分析的空间谱估计性能评价方法。从空间谱估计方法的处理性能和可实现性角度建立一种具有层次结构模型的性能评价准则,对各项性能评价指标做属性值规范化和权重系数模糊化处理,得到各评价指标的评价得分,累加得到处理算法性能量化评价的综合判决结果。基于仿真试验和某次海试试验结果,对常规波束形成(Conventional Beam Forming,CBF)、最小方差无畸变响应(Minimum Variance Distortion Response,MVDR)、多信号分类(Multiple SIgnal Classification,MUSIC) 三种空间谱估计方法进行评价,在较高输入信噪比和弱化计算量条件下,MUSIC为评价最优算法。试验结果表明,此评价方法可以按需求实现最优空间谱估计方法的选择。
空间谱估计;评价准则;模糊层次分析法;模糊三角数
0 引言
随着理论研究以及工程实践的开展,现已形成多种空间谱估计方法[1]。各种空间谱估计方法的性能,需经过实际的检验和客观的性能评价,所以需要建立相应的处理算法评价体系。对空间谱估计方法性能进行评价,给出数值化评价结果,为最终的处理性能比较提供依据,为技术的成果转化(提高声呐装备的低频探测能力、发展新型低频探测声呐系统)提供支撑。此外评价方法还可以应用到声呐装备的作战使用中,将不同的作战需求转化为评价方法中各个准则所占的比重,选出最佳的处理算法,以满足信息化作战的需求。因此,本文提出了一种基于模糊层次分析[2]的空间谱估计性能评价方法,为最优空间谱估计方法的选择提供一种技术支撑。
1 评价准则的建立
对空间谱估计方法进行评价,首先需建立评价准则,这里主要考虑两方面的性能评价需求,即处理性能和可实现性。构建的评价准则如图1所示,其中处理性能指标包括最小可检测信噪比、多目标分辨能力、方位估计能力、被动目标跟踪及被动目标定位能力;对于算法的可实现性,主要考虑算法的复杂性和模型/参数获取的可实现性。
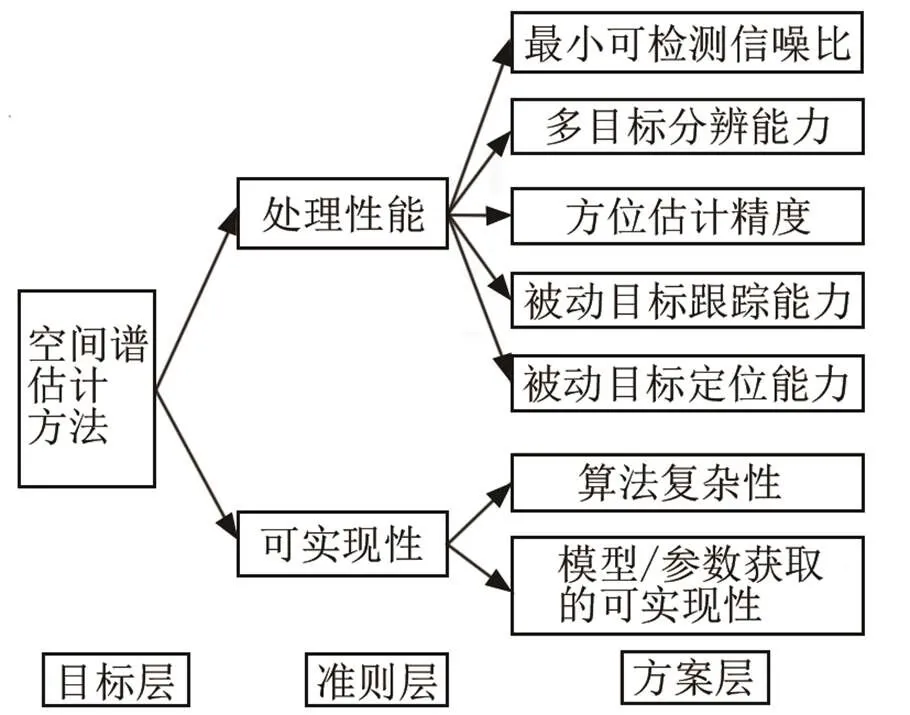
图1 空间谱估计方法评价准则
2 基于模糊层次分析的评价方法
现有的多种评价方法各具特色[3],但都包含两个关键要素:(1) 属性值归范化;(2) 权重系数。针对评价目标多准则且层次结构清晰的特性,采用模糊层次分析法作为权重向量赋值的方法。模糊层次分析法具有传统层次分析法的系统性、实用性和简洁性等全部优点,并且在评价中引入模糊性,是一种较理想的多准则评价方法。
层次结构模型参考图1评价准则,可分为目标层、准则层和方案层,其中准则层和方案层各指标可根据比较内容相应增减。使用的模糊层次分析法流程如图2所示。
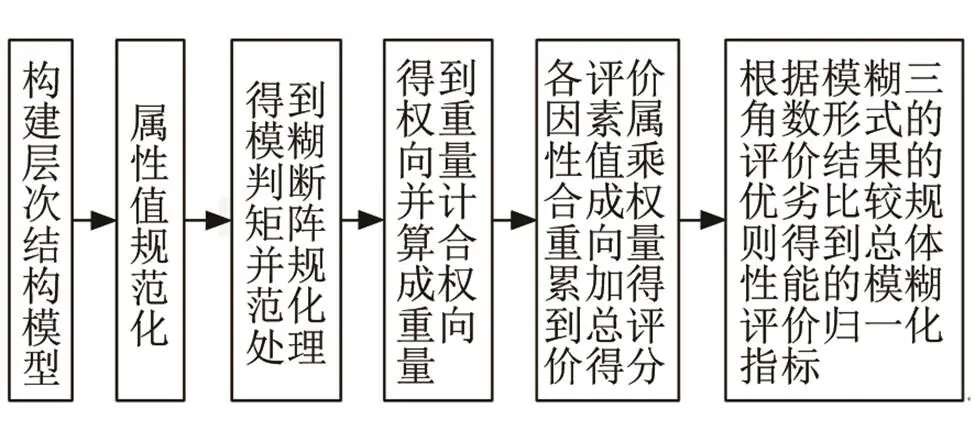
图2 模糊层次分析法评价流程
对不同空间谱估计方法的方案层相同因素做属性值规范化处理。属性通常分为效益型、成本型。属性值规范化公式有多种,下面列出其中一种,记为准则下方案的属性值规范化后的值[3]:
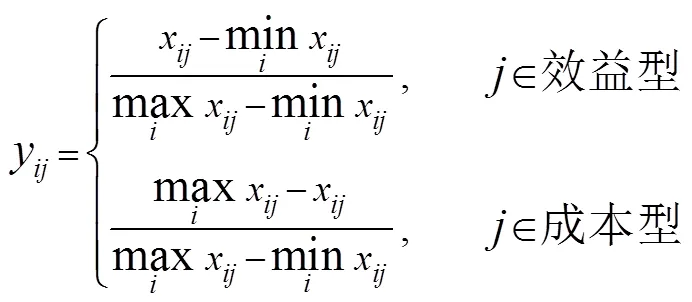
从准则层开始直到最底层的方案层,由领域专家对层中各因素两两比较,给出判断用数值(和是准则层和方案层中两两比较的归范化之后的属性值),得到准则层和各准则层下方案层的判断矩阵(指同一准则层下各方案层的总个数),结合模糊三角数[4]方法得到各模糊判断矩阵,其中三角数是描述各因素两两比较的模糊程度的数值,且有,,,其中是由模糊三角数规则得到的一个模糊数值区间,是确保模糊三角数区间在[0,1]的一个常数。
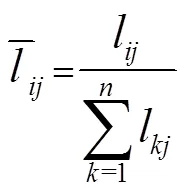
对模糊判断矩阵每行诸元求和,规范化之后即为各因素对上一层属性的权重向量[3]:
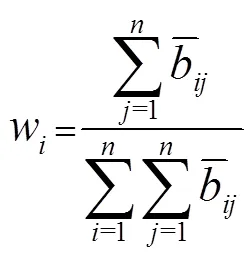
将不同处理方法的属性值规范化后的方案层各因素的值乘以各因素的合成权重向量,累加起来得到处理方法评价的最终得分,评价结果也是模糊三角数()的形式。
模糊三角数形式的评价结果的优劣比较采用以下规则,在乐观度,为评测人的乐观度)下计算模糊数均值[3]:

针对不同的处理方法,做归一化处理[3]:

3 仿真验证与海试试验
从最小可检测信噪比、可分辨能力、可检目标数、计算量四个方面对CBF、MVDR、MUSIC[5]三种空间谱估计方法的处理结果来测试评价方法,其中最小可检测信噪比与可分辨能力通过仿真给出,可检目标数从海试数据处理结果得到,计算量从三种空间谱估计方法理论公式[1]以及第三代信号处理机的一个C6678芯片环境下测试得到。
3.1 最小可检测信噪比
仿真条件:均匀线阵为64元,两目标分别为35°、45°方位的宽带信号,35°方位强目标的信噪比=10 dB,45°方位弱目标的从-30~10 dB逐渐增加,傅里叶变换点数为2 048,采样率为6 000,快拍数为128,处理频带为10~250 Hz,背景噪声采用白噪声。
图3(a)、3(b)、3(c)分别为CBF、MVDR、MUSIC三种算法的最小可检测信噪比测试结果,三种算法的最小可检测信噪比如表1所示。白噪声模型下,MVDR和MUSIC算法的最小可检信噪比能力相当,都明显优于CBF算法。

表1 三种算法的最小可检信噪比
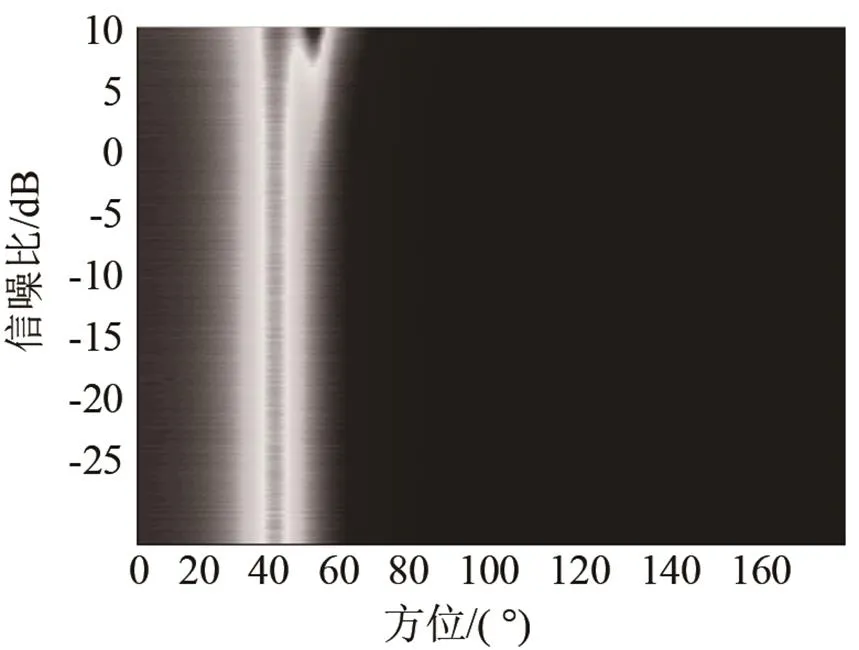
(a) CBF
(b) MVDR
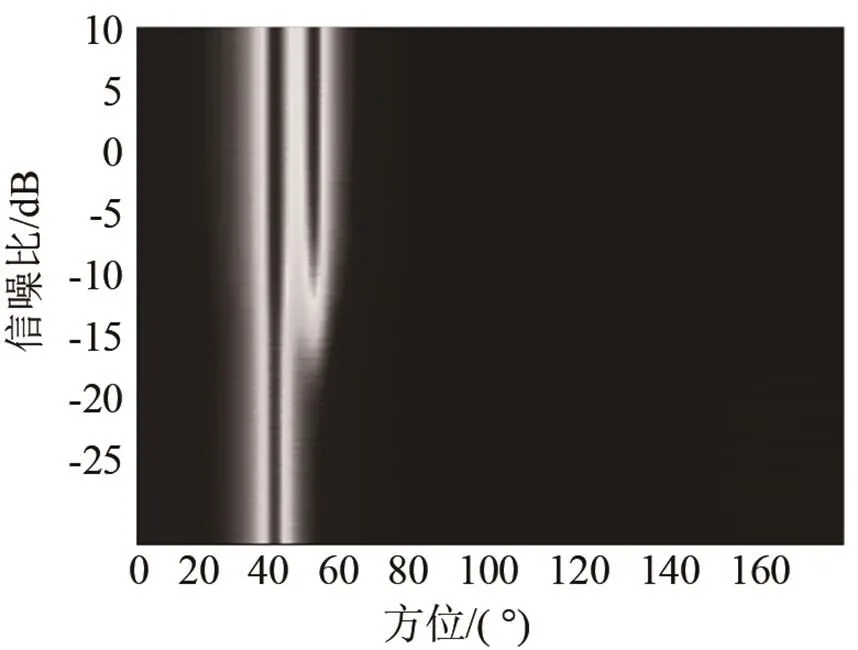
(c)MUSIC
3.2 可分辨能力
仿真条件:均匀线阵为64阵元,两目标为起始方位均在40°的宽带信号,其信噪比=[5 dB,5 dB],傅里叶变换点数为2 048,采样率为6 000,快拍数为128,处理频带为50~200 Hz,背景噪声采用白噪声。
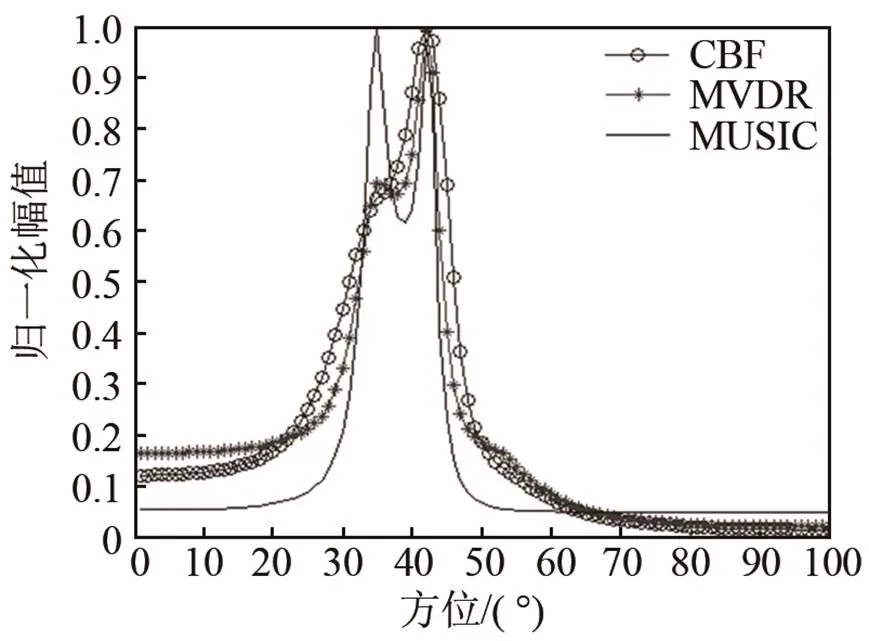
图4(a)~4(c)分别为CBF、MVDR、MUSIC三种方法的可分辨能力测试结果,图5(a)、5(b)、5(c)分别为三种算法可分辨两目标的起始数据批次,三种算法的可分辨能力如表2所示。在较高输入和白噪声模型下,MUSIC算法可分辨能力优于MVDR和CBF,且MVDR算法优于CBF算法。

(a)CBF
(b)MVDR

(c)MUSIC
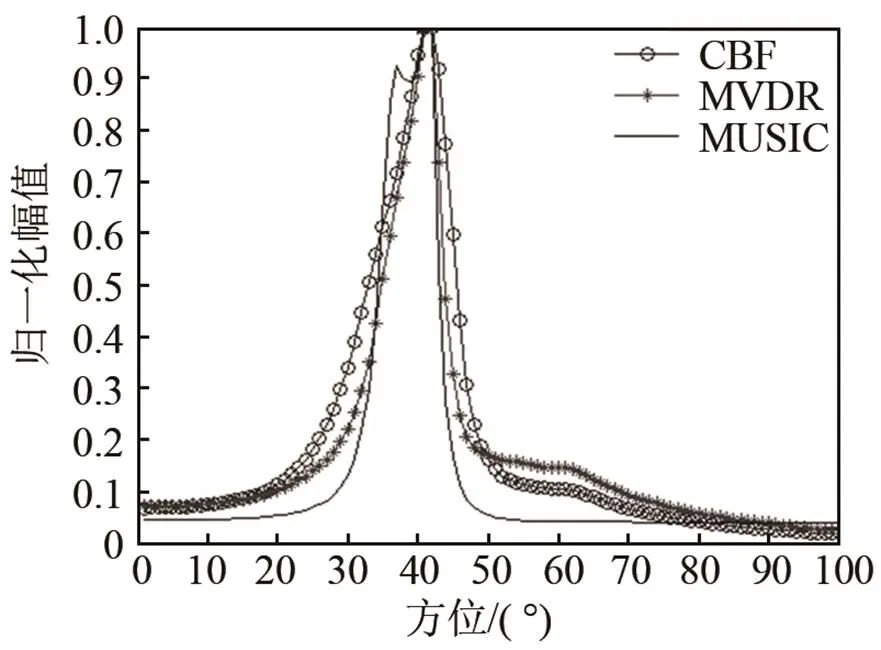
(a) MUSIC 135批数据可分辨
(b) MVDR 175批数据可分辨
(c) CBF 205批数据可分辨
图5 三种算法可分辨两目标的起始批次
Fig.5 The initial batch of data showing two targets identified by the three algorithms

表2 三种算法的可分辨能力
3.3 可检目标数
拖线阵海试数据处理。海试数据是在2016年6月份南海某海域试验得到,二级海况,试验声源固定位置,在方位历程上试验声源检测轨迹如图6(a) 中箭头所示。处理8 m阵元间距的数据,共40阵元,处理频带为10~100 Hz,采样率为16 kHz,傅里叶变换点数为8192,积分时间为40s。CBF、MVDR、MUSIC三种算法的处理结果如图6所示,其中MUSIC算法的固定信源数=10。

(a) CBF
(b) MVDR
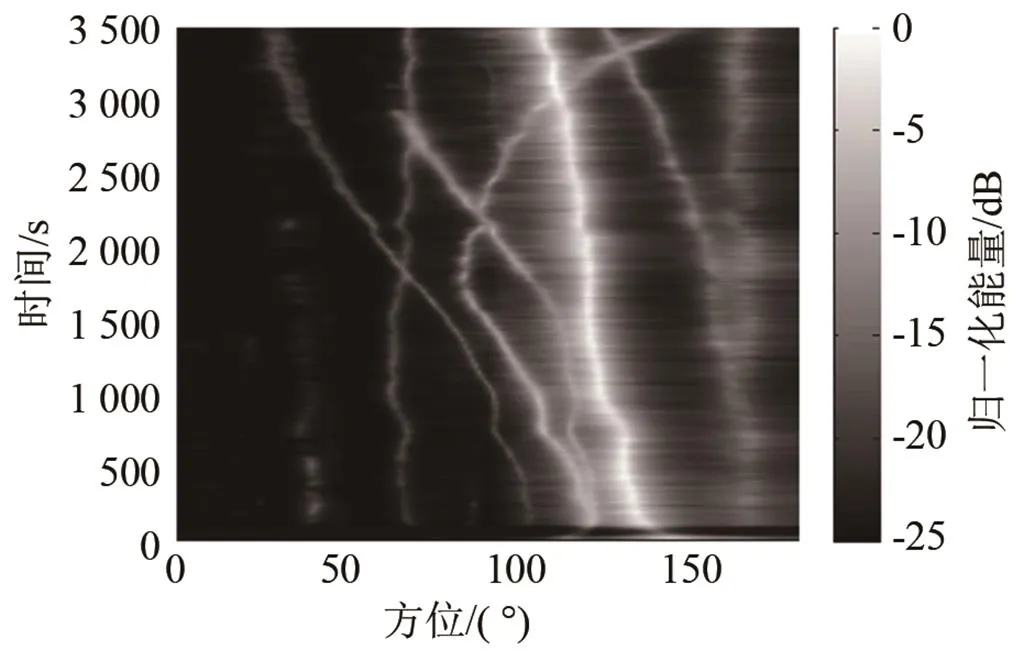
(c) MUSIC
三种处理方法得到的可检目标数统计如表3所示,从可检目标数这一处理性能上可以看出,MUSIC算法要优于MVDR和CBF,且MVDR算法优于CBF。

表3 三种算法得到的可检目标数
3.4 计算量
表4为三种算法的计算量统计[6],表中处理频点数为、扫描波束数为、阵元数为。

表4 三种算法计算量统计
取=64,=100,=256,MUSIC目标数取10,得到的计算量比值关系如表5所示,从表5中计算量比值关系上可以看出,MUSIC算法计算量明显大于MVDR和CBF算法的计算量,而计算量这一属性值属于成本性属性,即越小越优的属性。所以从计算量上看CBF算法要明显优于MUSIC算法、优于MVDR算法。
3.5 综合评价结果
基于最小可检测信噪比、可分辨能力、可检目标数、计算量四个准则归范化后的属性值对CBF、MVDR、MUSIC三种算法处理性能进行评价。结果如表6所示。乐观度取1/2时,重点考虑最小可检信噪比、可分辨能力、可检目标数等处理性能参数的影响,弱化计算量这一评价因素,此时MUSIC为评价最优算法。
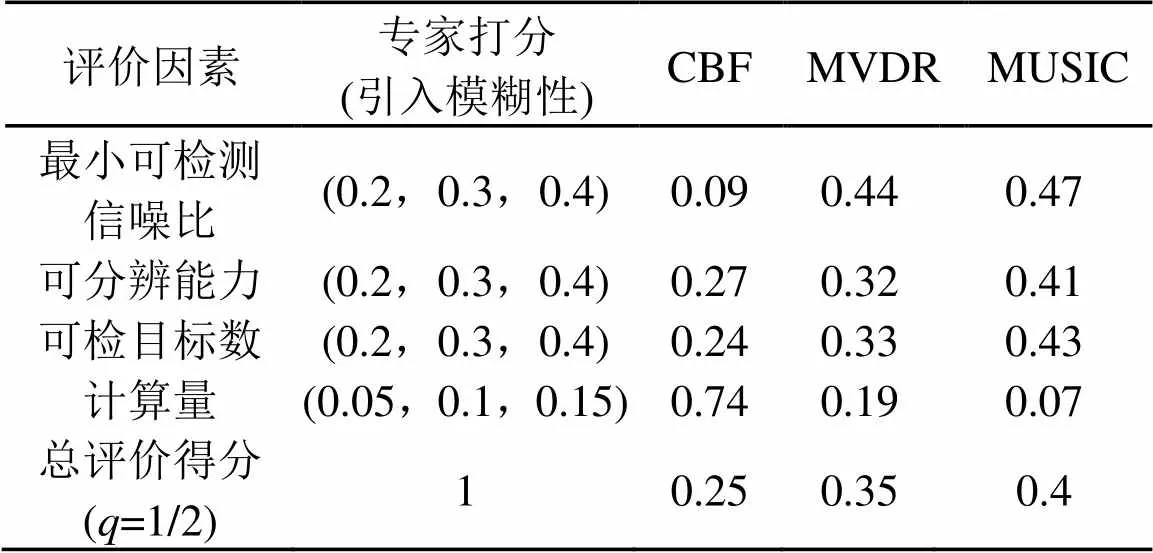
表6 三种算法的综合评价
4 结论
通过对仿真测试与某次海试数据处理结果的评价可看出,基于模糊层次分析的空间谱估计性能评价方法,可根据需求实现对现有各种空间谱估计方法的评价寻优,并给出了数值化评价结果,为最终的处理算法性能比较提供了依据;对新处理算法相对于现有方法的优化能力也提供了一种评价方法。本文仅是以CBF、MVDR、MUSIC算法为例,针对一种白噪声模型和一次试验数据给出的评价结果,要更好地验证各空间谱估计方法的性能优劣,还需对多种模型和多次试验数据处理结果进行评价,取评价结果的均值作为最终评价结果。
[1] 陈四根, 杨莘元. 阵列信号处理相关技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2004. CHEN Sigen, YANG Xinyuan. Research on array signal processing and its related technology[D]. Harbin: Harbin Engineering University, 2004.
[2] 洪昕晨, 林洲瑜, 张薇, 等. 基于应用层次分析法的森林公园叶声景评价研究[J]. 声学技术, 2016, 35(2): 91-94.HONG Xinchen, LIN Zhouyu, ZHANG Wei, et al. AHP based evaluation of leaf soundscape in forest park[J]. Technical Acoustics, 2016, 35(2): 91-94.
[3] 秦寿康. 综合评价原理与应用[M]. 北京: 电子工业出版社, 2003.QIN Shoukang. Principle and application of comprehensive evaluation[M]. Beijing: Publishing House of Electronics Industry, 2003.
[4] 李克文, 张郁, 马竟峰, 等. 基于模糊三角数模糊神经网络的软件质量评价方法[J]. 计算机工程与科学, 2014, 36(7): 1301-1306.LI Kewen, ZHANG Yu, MA Jingfeng, et al. Software quality evaluation method based on fuzzy neural network with fuzzy triangle numbers[J]. Computer Engineering and Science, 2014, 36(7): 1301-1306.
[5] 王学猛, 王斌. 二维Root-MUSIC算法的快速实现方法[J]. 声学技术, 2011, 30(6): 542-546.WANG Xuemeng, WANG Bin. Research on fast-realization of 2D Root-MUSIC algorithm[J]. Technical Acoustics, 2011, 30(6): 542- 546.
Genen H Golub, Charles F Van Loan. Matrix Computation[M]. Baltimore: The Johns Hopkins University Press, 1996.
Performance evaluation method of spatial spectrum estimation based on fuzzy analytic hierarchy process
WANG Qing1,2, ZHOU Bin1,2
(1. Hangzhou Applied Acoustics Research Institute,Hangzhou 310023, Zhejiang, China;2. Sonar Technology Key Laboratory, Hangzhou 310023, Zhejiang, China)
A variety of spatial spectrum estimation methods have been proposed. This paper puts forward a performance evaluation method for spatial spectrum estimation based on fuzzy hierarchical analysis to choose the optimal algorithm according to the requirements. A hierarchy structure model of performance evaluation criteria is established from the processing performance and realizability of beamforming algorithm. The standardization of the attribute values of various performance evaluation indices and the fuzzy processing of weight coefficients are conducted to obtainthe evaluation score of each evaluation index and then to accumulatethe evaluation scores for a comprehensive performance evaluation result of the processing algorithm. Based on the experimental results and a sea trial, the three spatial spectrum estimation algorithms of CBF, MVDR and MUSIC are evaluated, and under high input SNR and weakcomputing capacity, the MUSIC algorithm is evaluated as the optimum. The experimental results show that this evaluation method can be used to select the optimal beamforming algorithm.
spatial spectrum estimation; evaluation criteria; fuzzy analytic hierarchy process; fuzzy triangular number
TN 911.7
A
1000-3630(2017)-03-0281-05
10.16300/j.cnki.1000-3630.2017.03.015
2016-12-05;
2017-02-26
国防科技重点实验室基金(9140C240204150C24002)、973背景场项目(6132200303)
王庆(1990-), 男, 山东单县人, 硕士, 助理工程师, 研究方向为水声信号处理。
王庆, E-mail: wangqing2015019@163.com

