基于纵向超声导波管道非通透缺陷检测研究

童今鸣，胡明慧



基于纵向超声导波管道非通透缺陷检测研究

童今鸣，胡明慧

(华东理工大学承压系统与安全教育部重点实验室，上海200237)

管道经过长期服役后，由于磨损、腐蚀和意外损伤等原因，对管道正常运行产生危害。在实际工况中，小的腐蚀缺陷容易发展成腐蚀穿孔，浅层的小裂纹容易发展成穿透型裂纹，因此探究如何有效检测管道小宽度非通透缺陷是很有必要的。利用ANSYS有限元仿真软件模拟纵向模态导波对管道的周向和斜向非通透缺陷的检测，得到了周向非通透缺陷的反射系数曲线，并证实时间反转法可以显著提高导波对非通透斜裂纹的检测能力。还针对空管和充水管非通透斜裂纹的定位问题进行了研究，结果表明利用时间反转法可以得到缺陷较为精确的周向与轴向位置及大致形状。

超声导波；缺陷检测；纵向模态；管道；时间反转

0 引言

在石油、天然气等化工生产部门中，管道是很重要的组成部分，一旦管道发生破损、泄漏，可能会引发极其严重的后果，所以必须保证它们在安全的状态下运行。因此，对管材中缺陷的检测就成为了很重要的课题。超声导波技术是一种新型无损检测方法，可以对管道结构进行长距离快速检测。该方法既可以对管道上的泄漏点即穿透型缺陷进行识别和定位，同时也可以检测到影响管道使用寿命的非穿透型缺陷。管道中传播的导波可以分为纵向模态L(0，)、扭转模态T(0，)以及弯曲模态F(n，)，其中：是周向梯次，表示导波模态绕管壁螺旋式传播的形态；是模数，反映导波在管道厚度方向上的振动模态。马书义[1]等人研究了空心圆管中导波频率的选择。Harumichi Sato[2]等人利用数值方法模拟了导波在充水管道中的传播过程。刘增华[3]等人从理论上分析并得到了充水管道的频散特性曲线，并通过实验分析了充水管道中纵向模态的传播特性。

在实际检测中，经典导波技术很难检测出非通透型小缺陷，而这些小缺陷的存在会对管道的正常运行埋下很大的隐患。为了提高对小缺陷的检测灵敏度并对缺陷进行较精确的定位，很多研究人员进行了该方面的研究。Joel Harley[4]等人利用时间反转聚焦法实现管道健康监测，邓菲[5]等人提出了可以基于时间反转法进行管道导波缺陷参数的辨识，Takahiro Hayashi[6]等人利用时间反转法实现管道缺陷的成像，X Guo[7-8]等人提出了利用时间反转非线性导波检测法识别管道中的微观缺陷。纵向模态相比扭转模态更容易激励以及可重复，常被选择用来进行管道缺陷检测[9-11]。

本文在前人的基础上继续选择纵向模态导波针对管道中非通透裂纹的检测进行了数值模拟，采用时间反转法有效提高了管道中非通透斜裂纹的检测灵敏度，并且可以实现裂纹轴向和周向位置的精确定位以及裂纹形状的辨识。

1 基本理论

1.1 导波在管道中的基础理论

当波在圆柱壳结构中传播时，满足Navier位移运动方程[3]，即

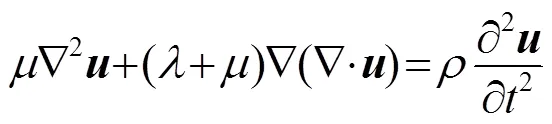
式中：、是材料的Lame常数；为材料密度；是时间；是位移场。

求解导波的位移场，归根结底就是求解式(4)所示的频散方程：

其中：与管径尺寸、材料的Lames常数、密度以及频率有关[10]。

1.2 空管道纵向模态的频散曲线

利用超声导波对空管道进行缺陷检测时，首先需要根据导波的频散曲线确定激励导波的模态与频率。利用英国帝国理工大学开发的Disperse软件可以很方便地得到管道中导波的频散曲线。

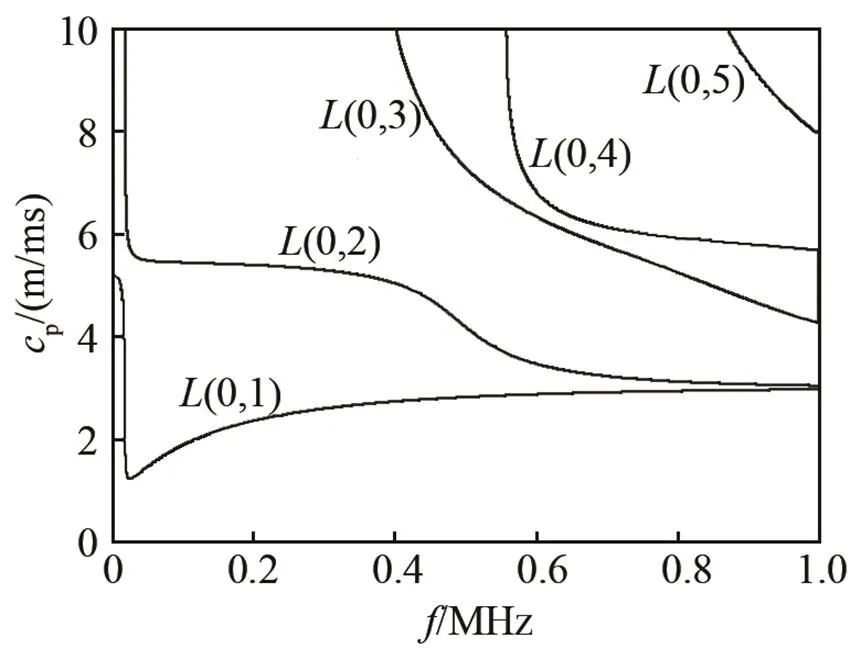
本文所研究的管道长度为2 m，外径和壁厚分别为100 mm和5 mm。材料参数：杨氏弹性模量为2.17×109Pa，泊松比为0.286，质量密度为7 930 kg/m3。将管道参数输入Disperse软件中即可得到管道纵向模态的相速度与群速度频散曲线，空管道纵向模态频散曲线如图1所示，图中坐标p表示相速度，g表示群速度。为了尽量避免激发导波频散性对检测结果的影响，因此应该选择频散很小的频率和模态作为激励导波。从图1中可见，L(0, 2)模态在低频段时，其频散曲线很平滑，频散性很小。综合考虑，选用导波的激发频率在70～260 kHz之间时，即可满足要求。

(a) 相速度

(b) 群速度

图1 空管L模态导波频散曲线

Fig.1 Dispersion curves of the L mode guided waves in hollow pipeline

1.3 充水管道中纵向模态的频散曲线

当管道中充满水后，由于纵向模态在水和管道中都可以传播，因此，管道中纵向模态的频散曲线由管道和水两者耦合而成。

利用Disperse软件绘制充水管道的参数输入与空管参数相同，充水管道模拟时需要输入水的密度1 000 kg/m3和水中纵波波速1 500 m/s，输完各项参数后即可绘制充水管道纵向模态的频散曲线，如图2所示。从频散曲线群速度中可以看出，当选择的频率范围在每个模态的群速度最大值范围内时(即管道中未受干扰的L(0, 2)模态分支部分)，其频散曲线较平缓，激发出的导波频散较小。

1.4 基于时间反转的导波检测

时间反转法是基于时间-空间聚焦效应提出的，是指接收传感器阵列接收声源发射的时域信号，将这些信号进行时间反转后再分别由相应的接收单元重新激励出去，它是声互易性原理的应用之一[12]，可以实现能量在空间、时间上的聚焦，从而获得声源位置并实现声源信号的重构。导波在管道中传播时，遇到缺陷会发生反射和透射，其中被反射回来的声波可以看作是以缺陷作为二次信号发射源的发射波，因此利用时间反转法将接收到的缺陷信号进行时间反转，然后分别由相应的接收单元重新激励，信号波会在传播至缺陷位置时发生能量聚焦。

(a) 相速度

(b) 群速度

图2 充水管道L模态导波频散曲线

Fig.2 Dispersion curves of the L mode guided waves in liquid-filled pipeline

2 导波的有限元仿真

利用ANSYS软件进行仿真，选择单元型号、确定材料参数、建立几何模型，然后对几何模型进行网格划分、设置好相应的边界条件、设定计算时间与时间步长，对模型进行计算分析。

2.1 模型建立

在模型建立阶段，可以通过软件特有的APDL编程语言进行前处理过程，也可以通过GUI界面进行模型的建立与加载。ANSYS软件中的Multiphysics模块还可以进行多物理场的耦合分析。本文研究的是管道中的一种典型缺陷：非通透型斜裂纹缺陷，图3为数值分析时选择的实体单元管道模型，其中缺陷的各项尺寸参数：缺陷长度为1/8管道周长，宽度为0.5 mm，径向深度为2.5 mm，缺陷中心点的位置距信号发射端1 m，缺陷与管道母线夹角为60°，周向位置为0°。在建立模型时为了保证激励出近似于单一L(0, 2)模态，管道圆周方向网格划分个数应为8的倍数，根据计算精度要求以及管道尺寸大小，选择合适的圆周方向网格划分个数，管道轴向单元的长度选择应满足单元尺寸必须小于激励模态波长的1/8，用以控制波形的传播误差在0.5%内。斜裂纹附近采用自由网格划分方式，其他区域采用扫略划分。

图3 缺陷管道模型

本文还重点探究了斜裂纹缺陷的一种特殊形式，即裂纹与管道母线成90°夹角的周向裂纹缺陷。

2.2 设置空管边界条件及求解计算

对于管道中纵向模态导波的激励方式，采用的是在管道一端所有节点上施加瞬时轴向位移载荷，由于施加的信号为轴对称均匀加载的方式，因此可以激发出近似于单一L(0, 2)模态的导波。信号接收端为距离发射端一个单元位置处的节点。

在管道激发端施加瞬时轴向位移载荷，管道另一端固定，载荷信号为经汉宁窗调制的10周期单音频正弦信号，施加位移的表达式如下[11]：

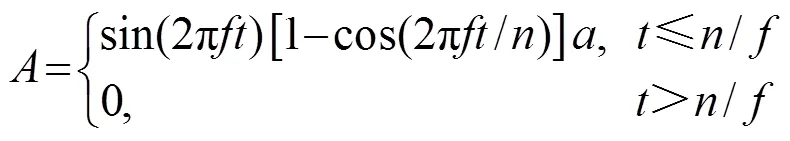
2.3 设置充水管道边界条件及求解计算

利用超声导波进行充水管道的损伤检测时，由于管道中传播的纵向L模态位移方向与管道轴线平行，且振动位移也很小，只有微米级，所以管道对管内液体的流动影响非常小，管内液体可以看成是稳定状态，而且，由于研究主要关注的是导波在管道中的传播特性，所以对管内液体建模时可以采取一定的简化。在对充水管道设置边界条件及求解计算时，管道部分的边界条件设置与空管道一致，即在管道一端施加瞬时位移载荷，另一端固定。管内液体两端设置为刚性边界条件，即将液体两端端面处所有节点位移设置为固定。管内液体与管道的交界面处则采用流固界面共节点。

图4 激励信号波形图

3 管道数值模拟

3.1 空管周向非通透缺陷检测

本节探究的是用导波检测空管中周向非通透缺陷的数值模拟。

利用频率为130 kHz的L(0, 2)模态导波检测周向长度分别为占管道圆周长度1/4、1/2、3/4和4/4的周向缺陷，得到的回波信号曲线如图5所示，从信号时程曲线可以看出，利用L(0, 2)模态导波可以有效地检测出具有一定长度的周向小宽度非通透缺陷。

(a) 裂纹长度占管道周长1/4

(b) 裂纹长度占管道周长2/4

(c)裂纹长度占管道周长3/4

(d)裂纹长度占管道周长4/4

图5 含不同周向长度裂纹缺陷管道的模拟检测信号

Fig.5 Simulated detection signals for the pipeline with a crack of different circumferential lengths

为了探究导波频率选择对检测结果的影响，继续选择180 kHz和260 kHz的频率进行空管周向缺陷数值模拟，得到的缺陷反射系数曲线如图6所示。由图6分析可知，当所检测的周向缺陷相同时，随着导波频率的增加，导波信号对周向缺陷的回波信号幅值呈现先增后减的趋势。当导波频率增加时，由于其相速度大致相等，所以波长变短，遇到缺陷时更加敏感，反射回的能量更多，所以会呈现回波信号增强的趋势。然而当导波频率继续增加的时候，导波在管道中传播时的能量衰减更加严重，所以会呈现出回波信号减弱的趋势。总的来说，在一定频率范围内，频率的改变对缺陷回波大小的影响并不是很大。从图6中还可以看出，当导波频率不变时，反射回波的幅值与周向导波的长度基本呈现线性关系。

图6 反射系数随裂纹长度的拟合曲线图

3.2 基于时间反转的空管斜向非通透缺陷检测

本节探究利用L(0, 2)模态检测管道斜向非通透裂纹的模拟研究。当管道中缺陷为非通透斜裂纹时，由于缺陷对于管道轴向的不对称性，缺陷反射回波的频散会很严重，导致缺陷回波幅值很小，在实际的检测过程中很可能被环境噪声信号淹没，因此有必要采取一定的方法提高缺陷反射回波信号。本文研究的缺陷如图3所示，并且保持缺陷中心点位置不变，不断改变其斜向角度，采用时间反转导波检测法来进行管道斜裂纹的检测，在数值模拟时采用的步骤如下：

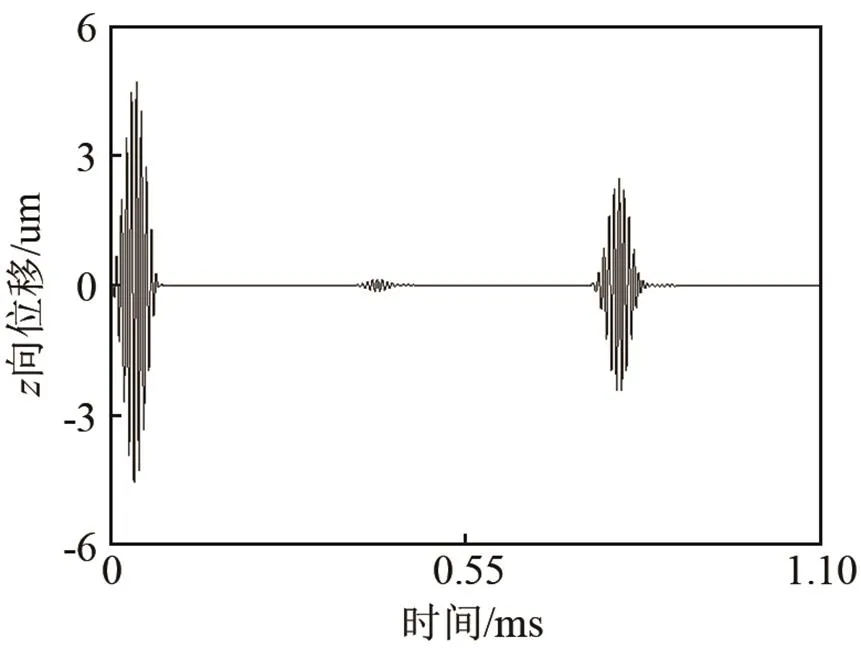
(1) 在建立的管道有限元模型上按照如前所述的激励方式激励出频率为130 kHz的L(0,2)模态导波进行缺陷检测，在48个监测节点上读取接收信号，将所有节点的信号直接叠加可以得到直接导波的检测信号。图7为部分旋转角度缺陷的信号曲线图，从图中可以看出，当裂纹角度小于75° 时，缺陷回波的幅值几乎不可见。

(a) 裂纹角度为90°

(b) 裂纹角度为75°

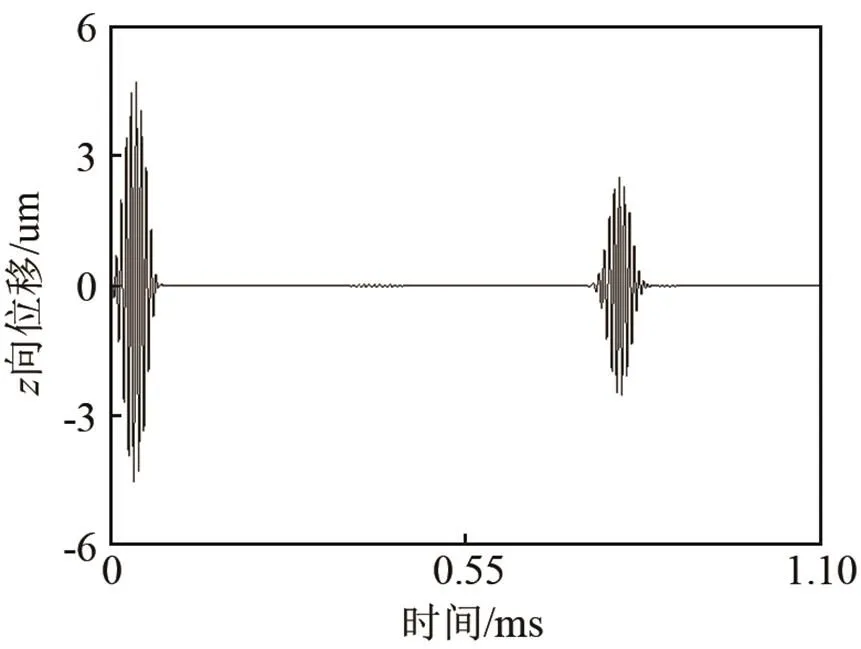
(c) 裂纹角度为60°

(d) 裂纹角度为45°

图7 含不同旋转角度斜裂纹缺陷管道的直接导波检测信号

Fig.7 Simulated direct detection signals for the pipelines with an oblique crack of different rotation angles

(4) 将时间反转激励信号同时在原模型管道端面的相应节点(与接收节点同周向位置所有节点)重新激励。而后在模型监测节点处提取所有节点的检测信号如图8所示。由图8可以看出，利用时间反转导波检测法可以有效地放大非通透型斜裂纹缺陷回波信号，特别是当斜裂纹角度大于45°时，时间反转导波检测法的信号放大效果很明显，对于小角度斜裂纹也可以从位移时程曲线中判断出缺陷波包的位置，从而进一步判断出缺陷的轴向位置。图9为使用两种检测方法得到的反射系数曲线，可以看出时反后缺陷反射系数有很明显的提高，说明利用时间反转导波检测法可以显著提高导波对管道斜裂纹非通透缺陷的检测能力。

3.3 非通透斜裂纹缺陷定位可视化研究

通过上述位移时程曲线图只能得到斜裂纹的轴向位置，而无法给出关于裂纹的周向位置以及裂纹的形状的有效信息，因此有必要对裂纹进行有效的定位研究。

3.3.1 空管斜裂纹缺陷定位可视化研究

利用时间反转法，选择旋转角度为60° 的非通透斜裂纹进行缺陷定位可视化研究，重复3.2节中的前三个步骤，在步骤(4)时建立另一个各项尺寸材料参数与被检管道相同但无缺陷的参考模型，并将步骤(3)中得到的时间反转激励信号同时在参考模型管道端面的相应节点(与接收节点同周向位置)重新激励。

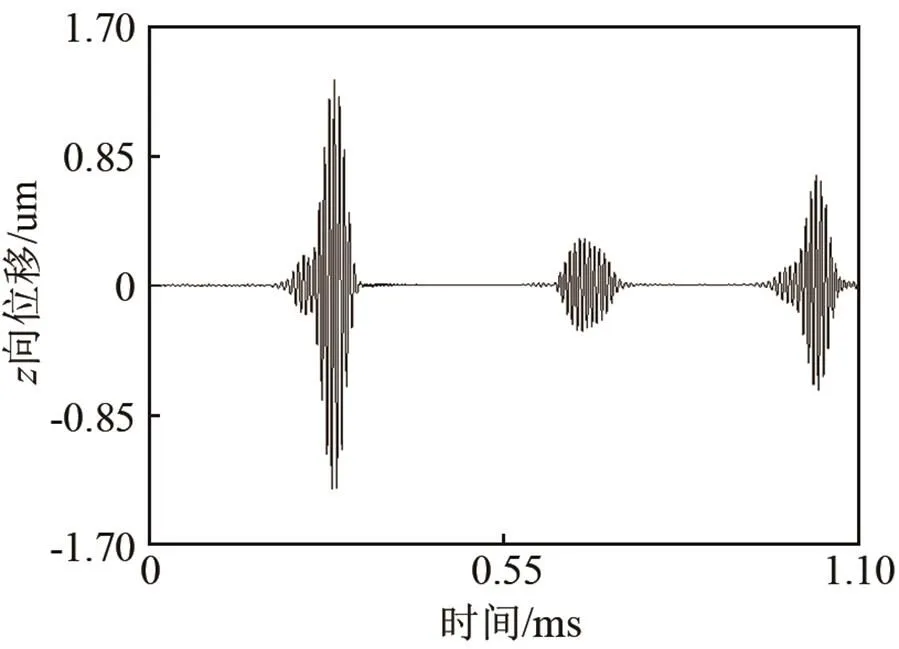
(a) 裂纹角度为90°

(b) 裂纹角度为75°

(c) 裂纹角度为60°

(d) 裂纹角度为45°

(e) 裂纹角度为30°

(f) 裂纹角度为15°

图8 含不同旋转角度斜裂纹缺陷管道的时间反转检测信号

Fig.8 Simulated time reversal detection signals for the pipelines with an oblique crack of different rotation angles

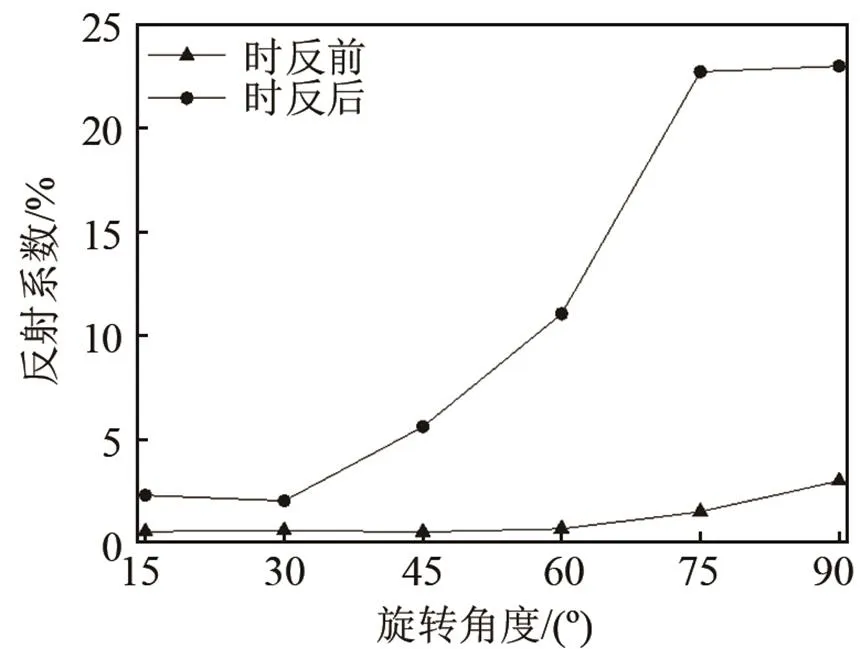
图9 时反前后反射系数随旋转角度变化的拟合曲线

根据时间反转聚焦效应的原理，可以知道如果信号按照原来的途径反向传播，那么信号最终会在波源处聚焦。因此，建立另一个管道各项尺寸材料参数相同但无缺陷的参考模型，将时间反转激励信号同时在参考模型管道端面的相应节点处激励，模拟再现缺陷反射波在管道中传播的逆过程，根据时间反转理论，可以推测出当信号传播到参考模型中与原缺陷所在的轴向位置相对应的位置时，信号能量会聚焦于源缺陷位置。计算出信号最大峰值传播到缺陷位置时的时间，而后读取该时间步下相应的位移,图10是信号传播到原缺陷相应轴向位置时的管道轴向振幅云图，从图中波形最大峰值处可以推断出缺陷的周向位置以及缺陷大致形状。

(a) 缺陷所在轴向位置局部放大图

轴向位移/m

(b) 管道位移云图

图10 空管道位移云图

Fig.10 Resulting displacement profiles for hollow pipeline

3.3.2 充水管道斜裂纹缺陷定位可视化研究

与空管缺陷定位所用的方法一样，充水管道缺陷也是采用时间反转法进行定位的，选择的管道模型与缺陷尺寸和空管道一致。图11为进行3.2节中的步骤(1)得到的某节点信号时程曲线，将时间反转后的节点信号，在另一个各项参数相同的无缺陷管道端部周向位置相同的各相应节点处激发，模拟缺陷回波逆传播的过程，如图12所示。图12为信号传播到原缺陷相应轴向位置时的管道轴向振幅云图。相对于空管而言，充水管道的时间反转聚焦效果会差一点，主要原因是因为管内液体对管道中传播的轴向模态与弯曲模态有一定的吸收，因此，会影响到信号波的聚焦效果。

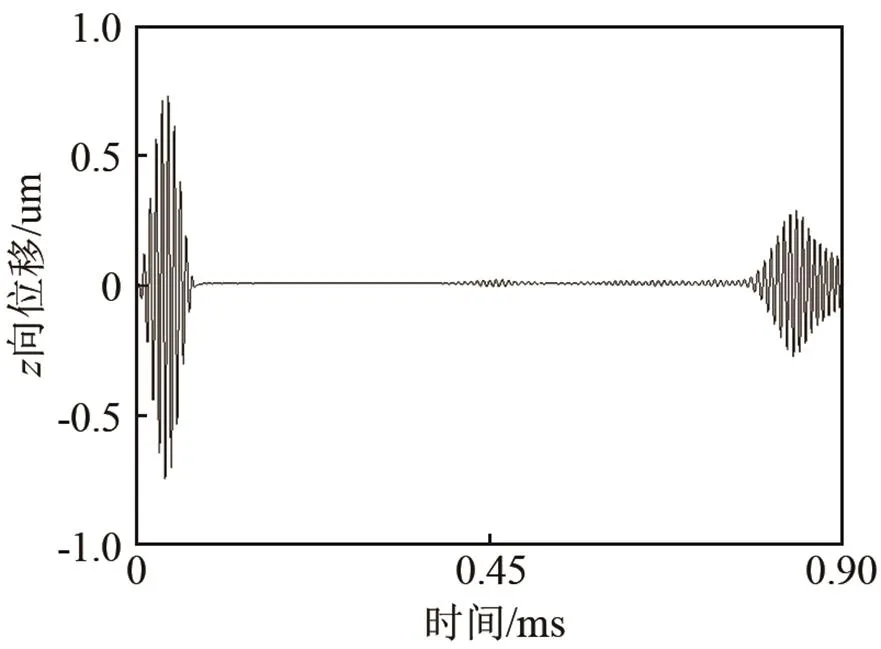
图11 节点接收信号

(a) 缺陷所在轴向位置局部放大图

轴向位移/m

(b) 管道部分位移云图

图12 充水管道位移云图

Fig.12 Resulting displacement profiles for liquid- filled pipeline

3.4 试验研究

图13 试验流程示意图

试验选用长度2 000 mm、壁厚3.5 mm、外径76 mm的钢管，在管道距激发端600 mm处加工一尺寸为30 mm×2 mm×2 mm、与管道母线偏转75°的不通透斜裂纹。压电晶片贴在管道端部外表面上，为了尽可能多地得到管道周向不同位置的缺陷回波信号，使后续聚焦效果较好，使用32片压电陶瓷晶片组成导波传感器阵列，并将所有压电陶瓷晶片按照顺序依次编为1～32号，将编号为奇数的压电晶片归为A组，编号为偶数的压电晶片归为B组。在进行导波试验时，先将A组所有晶片用于激发导波，B组所有晶片用于接收，得到16个接收信号后，再将B组所有晶片用于激发导波，A组用于接收信号，得到16个接收信号，这样可以得到管道周向32个位置处的接收信号。本试验分别在激励频率110～170 kHz、步长10 kHz下完成，由于在140 kHz激励频率下获得的检测波形最清晰并且信噪比较高，所以本试验采用该检测频率进行信号采集。图14为某接收点接收信号和32个接收点接收到的缺陷波形信号。

(a) 某接收点接收信号

(b) 32个接收点上获得的缺陷反射信号

图14 带斜裂纹管道检测波形图

Fig.14 The time domain waveforms for the pipeline with oblique crack

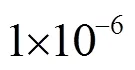
(a) 缺陷所在轴向位置局部放大图

轴向位移/m

(b) 管道部分位移云图

图15 管道位移云图

Fig.15 Resulting displacement profiles for the pipeline with oblique crack

4 结论

本文利用有限元软件探究了纵向模态对管道缺陷检测时的传播特性，并基于时间反转理论，对空管和充水管中的缺陷进行了定位研究，主要得出了以下结论：

(1) 利用纵向模态检测空管中的周向非通透缺陷时，缺陷回波与缺陷长度基本成线性关系，改变检测频率对缺陷检测效果影响不明显。

(2) 基于时间反转导波检测法可以有效放大非通透斜裂纹的回波信号，提高对非通透斜裂纹的检测能力。

(3) 利用时间反转法可以对空管和充水管中的裂纹进行有效的轴向和周向定位，并可根据轴向振幅云图确定缺陷的大致形状。

(4) 利用试验验证了缺陷成像法具有实际可行性。

[1] 马书义, 武湛君, 刘科海, 等. 空心圆管中导波频散特性与检测频率的选择[J]. 机械工程学报, 2014, 50(20): 8-17. MA Shuyi, WU Zhanjun, LIU Kehai, et al. The dispersive characteristics of guided wave and the detection frequence selection[J]. Journal of Mechanical Engineering, 2014, 50(20): 8-17.

[2] Sato H, Ogiso H. Theoretical and simulated analysis of guided waves propagating in fluid-filled pipes[J]. Japanese Journal of Applied Physics, 2010, 49(7): 1-6.

[3] 刘增华, 何存富, 杨士明, 等. 充水管道中纵向超声导波传播特性的理论分析与实验研究[J].机械工程学报, 2006, 42(3): 171-178.LIU Zenghua, HE Cunfu, YANG Shiming, et al. Theoretical analysis and experiment study on propagation characteristics of longitudinal ultrasonic guide wave in liquid-filled pipeline[J]. Journal of Mechanical Engineering, 2006, 42(3): 171-178.

[4] Harley J, O'Donoughue N, Jin Y, Moura J M. Time reversal focusing for pipeline structural health monitoring[C]//Proceedings of Meetings on Acoustics Acoustical Society of America, 2010, 8(1): 30001-30008.

[5] 邓菲, 吴斌, 何存富. 基于时间反转的管道导波缺陷参数辨识方法[J]. 机械工程学报, 2010, 46(8): 18-24. DENG Fei, WU Bin, HE Cunfu. The defect parameter identification method of pipeline guided wave based on time reversal[J]. Journal of Mechanical Engineering, 2010, 46(8): 18-24.

[6] Hayashi T, Murase M. Defect imaging with guided waves in a pipe[J]. J. Acoust. Soc. Am., 2005, 117(4): 2134-2140.

[7] GUO X, ZHANG D, ZHANG J. Detection of fatigue induced micro-cracks in a pipe by useing time-reversed nonlinear guide waves: A three-dimensional model study[J]. Ultrasonics, 2012, 52(7): 912-919.

[8] Guo X, Yang D, Zhang D. Microcrack localization in pipelines using nonlinear guide waves combined with time reversal[J]. J. Acoust. Soc. Am., 2012, 131(4): 3511.

[9] 李伟. 超声导波管道缺陷检测的数值模拟及实验研究[D]. 北京: 北京工业大学, 2007. LI Wei. Simulation and experimental research on pipe defect detection by using ultrasonic guided waves[D]. Beijing: Beijing University of Technology, 2007.

[10] 赵乃志. 利用压电超声导波时间反转法的管道结构裂纹监测研究[D]. 大连: 大连理工大学, 2013. ZHAO Naizhi. Research on pipeline structural crack monitoring by using PZT-based ultrasonic guided waves time reversal method[D]. Dalian: Dalian University of Technology, 2013.

[11] 齐霁. 基于PZT超声导波的多裂纹管道损伤识别研究[D]. 沈阳: 沈阳建筑大学, 2013. QI Ji. Research on multiple crack pipeline monitoring by using pzt-based ultrasonic guided waves[D]. Shenyang: Shenyang Jianzhu University, 2013.

[12] Fink M. Time reversal of ultrasonic fields-Part I: Basic principles[J]. IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 1992, 39(5): 555-566.

Detection of non-penetrating defect in pipeline based on the longitudinal ultrasonic guided wave

TONG Jin-ming, HU Ming-hui

(Key Laboratory of Pressure Systems and Safety, East China University of Science and Technology, Shanghai 200237, China)

The wear, corrosion and accidental damage will harm the normal usage of the pipeline after long term operation. Under the practical working conditions, the small corrosion defects can be easily developed into corrosion perforation. Meanwhile, small crack in the shallow layer is likely to develop into a penetrating crack. Therefore, research on how to effectively detect the small defects in pipeline is necessary. In this paper, the longitudinal ultrasonic guide wave based detections of circumferential and oblique non-penetrating defects are simulated by ANSYS finite element simulation software. The reflection coefficient curves of circumferential non-penetrating defects are obtained. Itis also proved that the time reversal method could considerably increase detection capability to the oblique non penetrating defects. This paper also investigates the localization problem of the oblique non penetrating defects in hollow pipeline and liquid-filled pipeline. The result indicates that by the time reversal method, the more accurate circumferential and axial positions and the approximate shape of the defect can be obtained.

ultrasonic guided wave; defect detection; longitudinal model; pipeline; time reversal

TB553

A

1000-3630(2017)-03-0238-09

10.16300/j.cnki.1000-3630.2017.03.008

2016-11-29;

2017-03-16

国家自然科学基金(51205133)资助项目

童今鸣(1994－), 男, 江西上饶人, 硕士研究生, 研究方向为管道缺陷导波检测。

胡明慧, E-mail: agile_hu@ecust.edu.cn