孤子局域共振激发的一种物理模型
王少华,刘昊华,沈月龙
孤子局域共振激发的一种物理模型
王少华1,刘昊华1,沈月龙2
(1. 南京大学声学研究所,江苏南京210093;2.中国海洋大学信息科学与工程学院,山东青岛266100)
作为非线性领域的重要内容,孤子自从被发现以来就得到了广泛的关注。虽然目前关于孤子的传播及其相互作用性质等方面的研究已经相当成熟,但是对于孤子的产生问题仍然没有系统的认识。孤子产生问题的深入研究,不仅对于理解自然界及物理系统中的非线性现象十分重要,对孤子现象的工程应用也极为重要。基于这些原因,一些孤子激发方法的研究不断被提出。在非线性阵列带隙中的能量超透射现象激发孤子理论的基础上,局域共振孤子激发的方法被提出。该方法通过在半无限长-FPU链中加入缺陷来引入局域共振机制,不仅有效降低了孤子激发的临界驱动振幅,还实现了孤子激发的可控操作。然而,虽然理论分析与数值模拟都证明了这一方法的可行性,但关于该方法的相关实验验证还是空白。为了进一步将该方法推向实际实验,提出了一种简易可行的实验方案,并做了深入的理论分析与大量的数值模拟。该方案给出一种物理模型,该模型以线性弹簧为基本元件,利用结构的几何非线性来构建-FPU链,并以耦合摆阵列来实现。通过大量数值模拟证明了该方法的可行,同时研究了孤子释放周期与驱动频率、振幅的关系,结果与前述理论一致。此外,还通过数值模拟研究了孤子的激发周期与缺陷处阻尼大小的关系,以及单元质量不均匀性对孤子激发与传播的影响,为进一步实验提供依据。
孤子;-FPU链;局域共振;耦合摆
0 引言
随着孤子问题研究的不断深入,人们对孤子的存在、传播以及相互作用特性等问题已经有了充分的认识[1-3]。孤子是自然界中常见的非线性现象,并且可以用来解释诸如神经信号的传递等生命科学的相关问题[4]。然而,要深入理解孤子相关现象,实现孤子的实际应用,就要进一步研究孤子产生的机理和激发的方法。虽然在可积系统里,给定合适的初始条件便可得到孤子,但是现实的物理系统往往是不可积的,而且很难精确地给出合适的初始条件来控制孤子的激发,因而寻找实验上可行的有效激发孤子的方法很有必要。
一些孤子激发的新方法不断被提出,其中Leon[5-6]等人提出在边界处施加驱动来激发孤子的方法,使孤子激发的可操作性大大增强。这种方法的内在机制是边界驱动激发的渐消波(evanescent wave)在驱动幅度超过某一临界值时会产生鞍结分岔,激发孤子[7]。在这种方法的基础上,Yu[8]等人提出局域共振的方法实现孤子的可控激发。
根据文献[8]的理论,在半无限的-FPU链一端引入缺陷,并给予频率靠近其通带频率下限的简谐位移驱动,当驱动频率接近局域模本征频率时,缺陷处发生局域模共振,局限于缺陷处的能量不断累积,最终穿透禁带,以孤子的形式释放出去。能量累积的速率与驱动条件相关,因而可通过改变驱动振幅与频率调节孤子释放周期。该方法不仅驱动参数明确简洁,易于调控,使得孤子的激发更具可控性,而且具有所需驱动幅度低、能量转化效率高等优点。局域共振激发孤子的方法与光波导阵列[9]和非线性传输线系统[10-11]中的边界局域激发方式有着很大的相似性,其研究意义不仅仅局限于FPU链系统。
鉴于该方法的优势,我们提出一种实验上简易可行的物理模型来实现-FPU弹簧链中局域共振激发孤子。该模型以线性弹簧为基本元件,利用结构的几何非线性来构建-FPU链,并通过耦合摆阵列来实现。
1 物理模型
1.1 非线性弹簧链
-FPU弹簧链中质点运动方程如式(1)所示[8]:
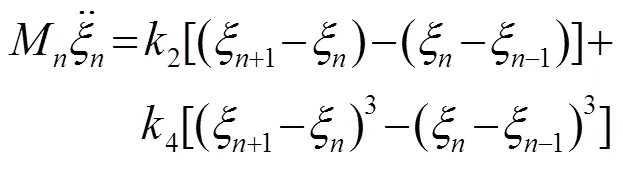
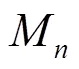
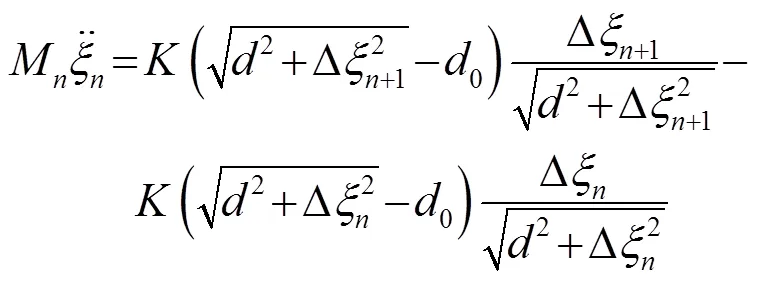
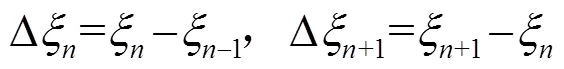
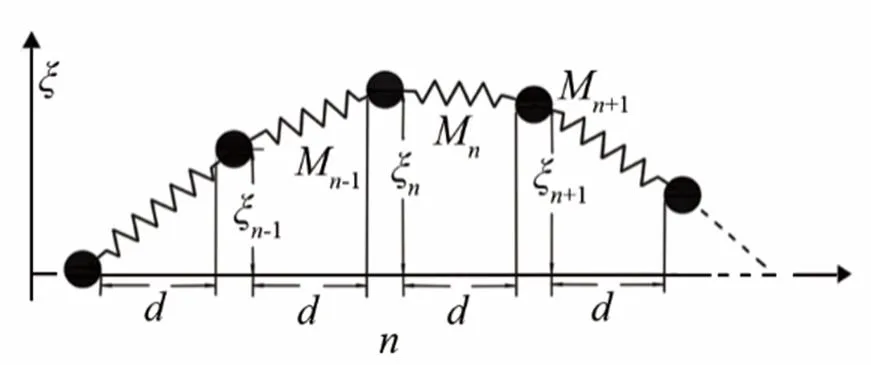
图1 非线性弹簧链示意图(横轴为弹簧链初始位置,纵轴为质点振动方向)
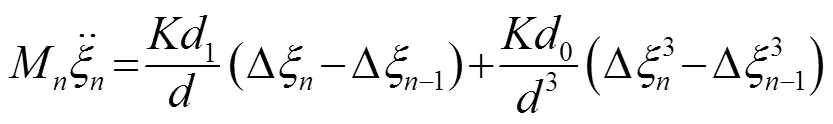
小振幅近似下该结构等效于-FPU链。
1.2 非线性弹簧链耦合单摆
上述模型要求质点振动约束在横向振动方向上,同时不引入过大摩擦,考虑小幅振动下的耦合摆结构来实现这一模型。非线性耦合摆系统中孤子实验已经有很多[12-16],然而大多数模型在考虑单元间耦合力的同时不能忽略重力作用,其运动方程与式(1)有很大不同,并不能直接用来实现包络孤子局域共振激发。将讨论的结构与其有显著区别:(1) 弹簧中引入了预伸长,从而使得弹力中出现位移的一次项成分;(2) 本文所述模型考虑摆的小幅度振动,摆杆末端近似于局限在水平面内运动,重力影响十分微弱;(3) 弹簧弹性系数较大,弹性力起主要作用。模型结构如图2所示。
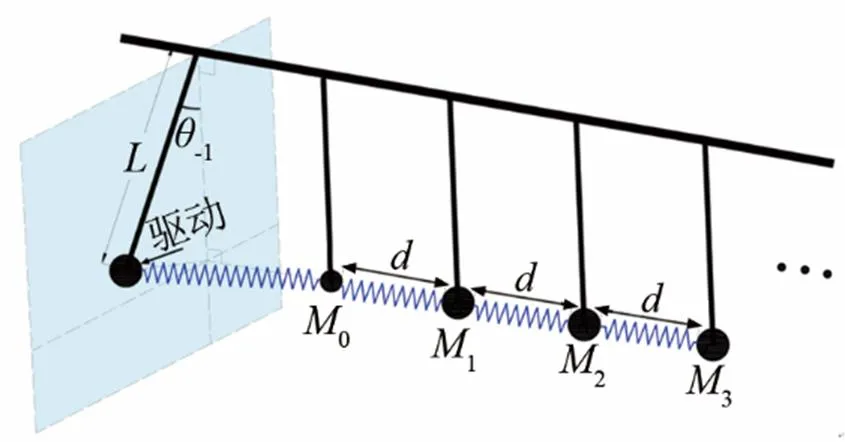
图2 模型结构示意图
图2中,一系列单摆以轴承悬于同一水平杆上,其末端由劲度系数为的弹簧耦合起来。每个单摆由长为的摆杆和半径为的质量块构成。单元间隔,其中0是弹簧的自由长度,1是弹簧在平衡位置的预伸长。图中第一个单摆受到外界驱动,第二个单摆(即图中质点0所标注单摆)处引入质量缺陷,即其质量块质量与其他各处不同。受力分析得第根摆杆的动动方程为
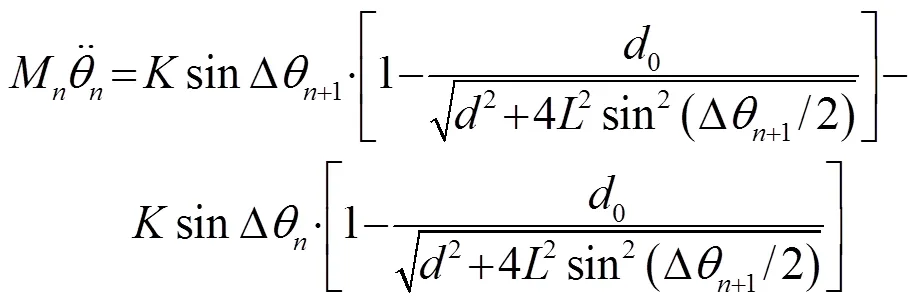
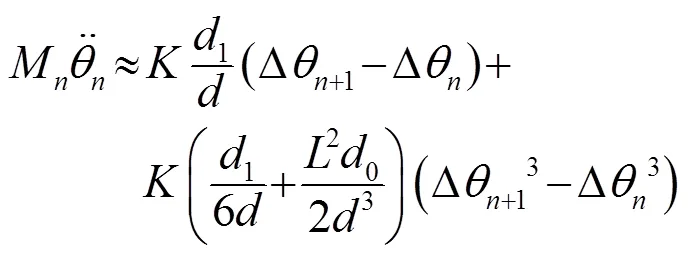
从而式(5)可近似为式(6),与前述式(1) 的形式相同。
1.3 实验影响因素的分析
上述模型中并未考虑实际实验中现实因素的影响,这些影响可能会对实验结果产生影响,有必要对其进行分析。
摆杆在摆动过程中,重心会在竖直方向上发生变动,其重力力矩显然不恒为零,因而会对运动方程造成影响,有必要对其进行分析。根据力矩定义可得,第根摆杆的重力力矩为
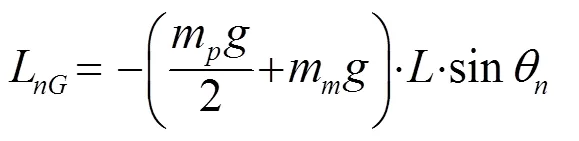
系统中各种阻尼是必须要考虑的因素。该系统中,空气阻力与轴承的摩擦力是阻尼的主要来源。忽略摆杆末端质点形状的影响,第根摆杆受到的空气阻力力矩[17]为
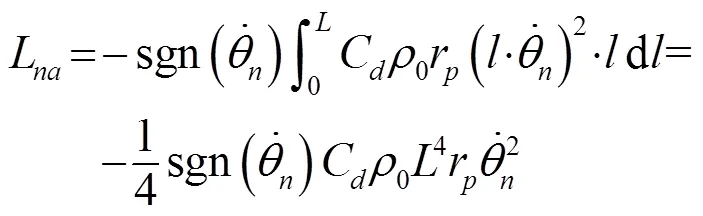
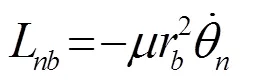
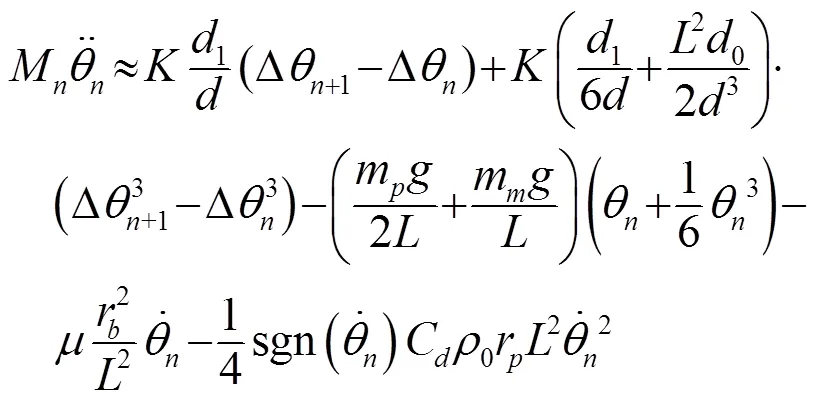
为了分析以上各量对系统运动方程的影响,将重力力矩、空气阻力力矩与轴承摩擦力矩分别与式(6)中弹性力力矩进行量级比较。为此,在前面假设的基础上,考虑实验现实,先给出系统中各参数的取值如表1所示。
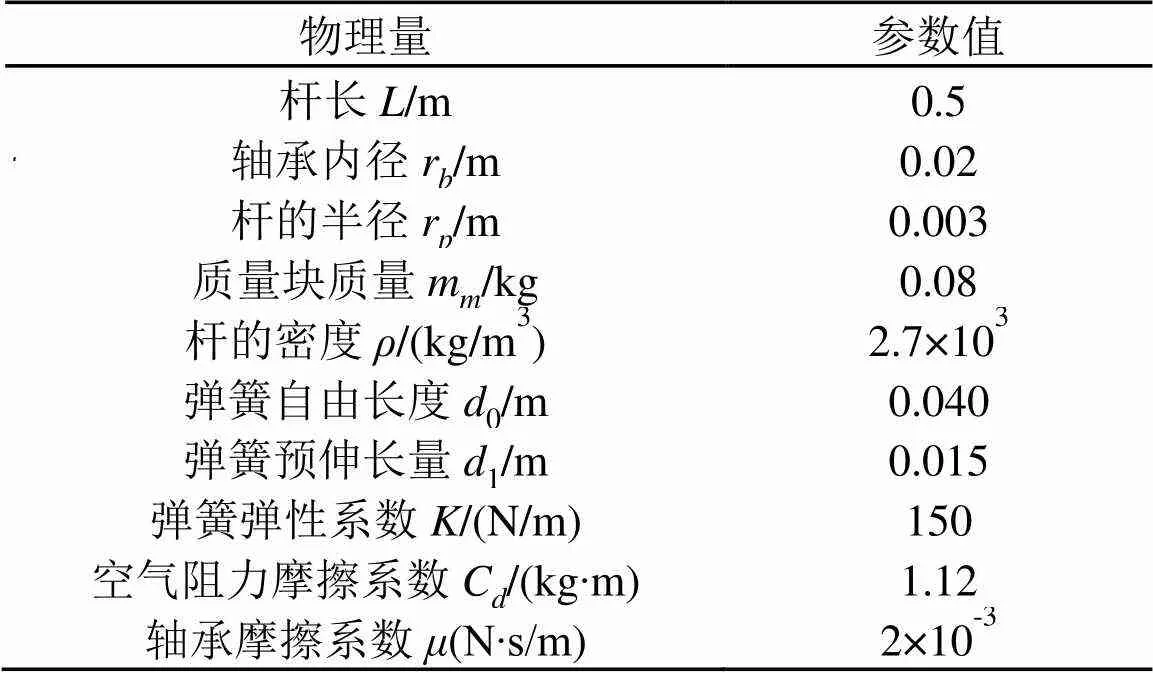
表1 模型结构参数
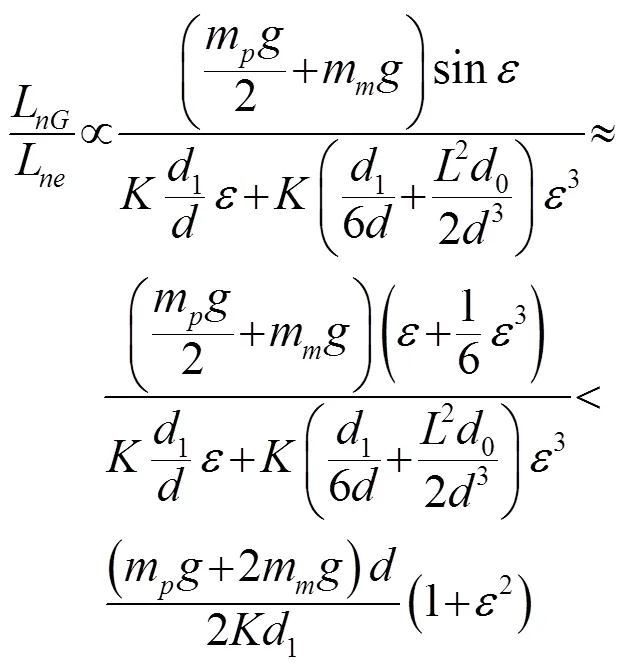
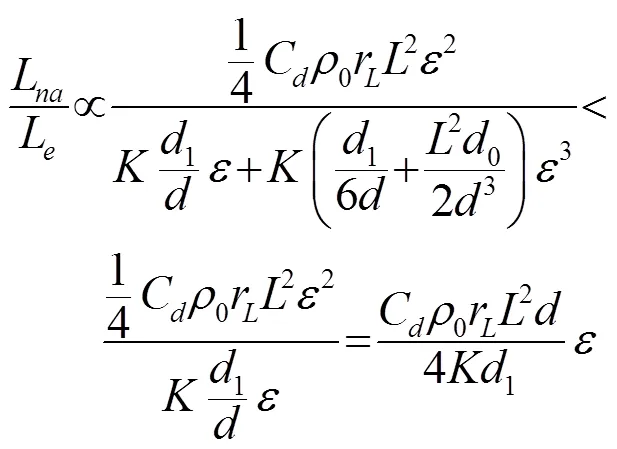
除了上述因素,影响系统实验结果的因素还有很多,诸如摆杆非绝对刚性,系统单元质量以及摆杆长度的不均匀性等,经过另外的分析,我们确定了这些因素可以控制在合理范围内。
2 数值计算结果
2.1 无量纲化
为简化运动方程形式,同时方便下文数值模拟结果与文献[8]的结果进行对比,利用式(14)
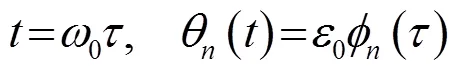
对式(10)做变量代换得:
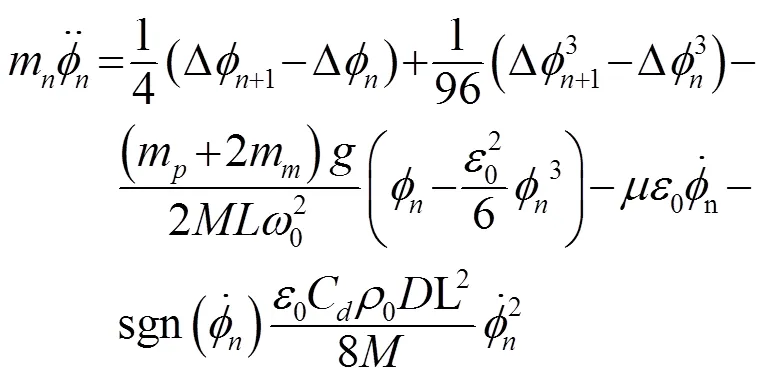
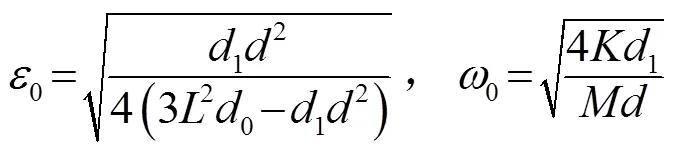
其中,为非缺陷处的单摆等效质量,为各单元质量相对于归一化后的等效质量。根据局域共振理论,=0处为质量小于普通质点的质量缺陷,因而满足关系:
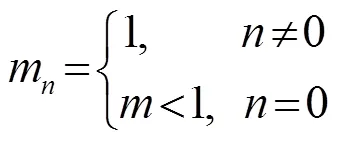
其中,=-1处为位移驱动,显然边界处(即=0处)质点运动方程与其他各处不同。令表示边界位移驱动引起的摆杆摆动角度,则小振幅驱动()时驱动处摆杆末端近似有,即位移驱动可表示为
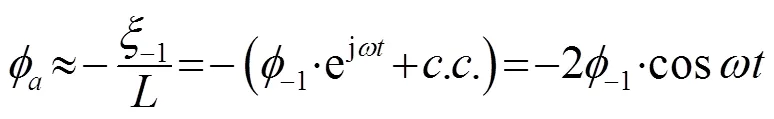
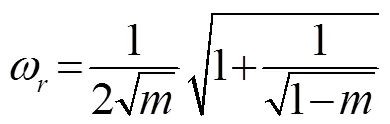
缺陷处质点的运动方程,即边界运动方程如式(20)所示(这里是直接引用式(15)在缺陷处的情形,即下标取作0时的情形):
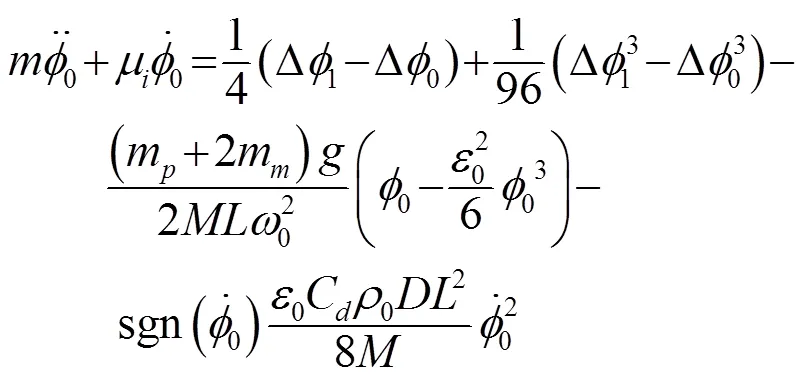
其中,μ为缺陷处的阻尼系数。
2.2 孤子的激发与传播
式(15)与式(20)分别为弹簧链中摆杆及边界处摆杆的运动方程,将表1中各参数分别代入两式,采用变步长的四阶Runge-Kutta法进行数值模拟。模拟中取单元个数为130个,并在末端30个单元加入适当阻尼来衰减反射波。
图3给出了孤子激发的空间及时间波形图。所有图形均是在缺陷质量=0.7、驱动幅值-1=0.35、以及Δ=0.08的条件下得到的。图3(a)中三幅图分别为三个不同时刻前100个质点的位移分布。图中红色点表示缺陷质点(=0),黑色点表示普通质点(≠0),蓝色点表示位移驱动(=-1)。图3(b)则是=15处的质点位移随时间的变化图。由图中可看出,孤子能够在弹簧链中稳定传播,孤子振幅远大于驱动振幅,且释放周期基本稳定,这些均与文献中的结论一致。
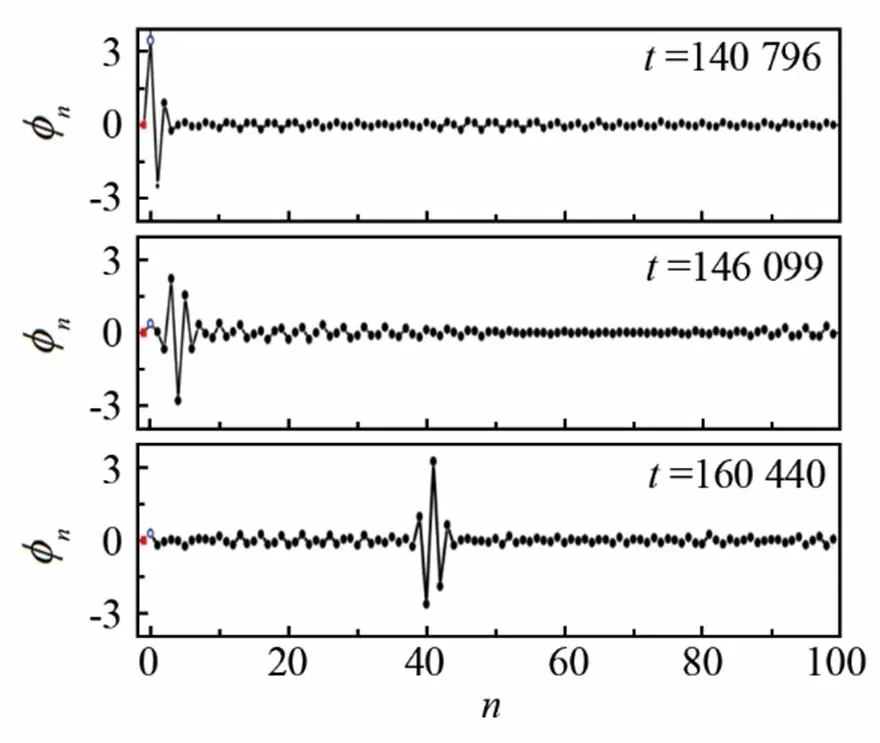
(a) 不同时刻前100个单元的位移分布图
(b)=15处的时间波形图
图3 孤子空间与时间波形图
Fig.3 Waveform of solitons in space and time domains
2.3 孤子激发的临界驱动强度
图4给出了不同驱动频率下孤子激发的临界驱动强度(图4(b)),与文献[10]中所述的理想-FPU链模型(图4(a))对比。本文所述模型的临界驱动强度以ϕ表示,而文献[10]所述模型的临界驱动强度以表示。各图中四条曲线分别表示缺陷质量=0.7、0.75、0.8、1.0时的临界驱动强度随驱动频率变化的趋势。当=0.7、0.75、0.8时,由式(14)得局域模本征频率分别为=1.004 6、1.0、1.005 6,由图可知,两图中这三条曲线中临界驱动强度均随着驱动频率偏离局域模本征频率逐渐增大,基本成线性递增趋势;两图中=1时的临界驱动强度均明显大于其他三种情形,其曲线变化趋势与其余曲线稍有不同,反映出有无缺陷时孤子激发机制有所不同。然而,仔细比较图4(a)与图4(b)可发现,相同频率下,图4(b)中临界驱动强度大都小于图4(a),即耦合摆模型的临界驱动强度小于理想-FPU链模型的值。
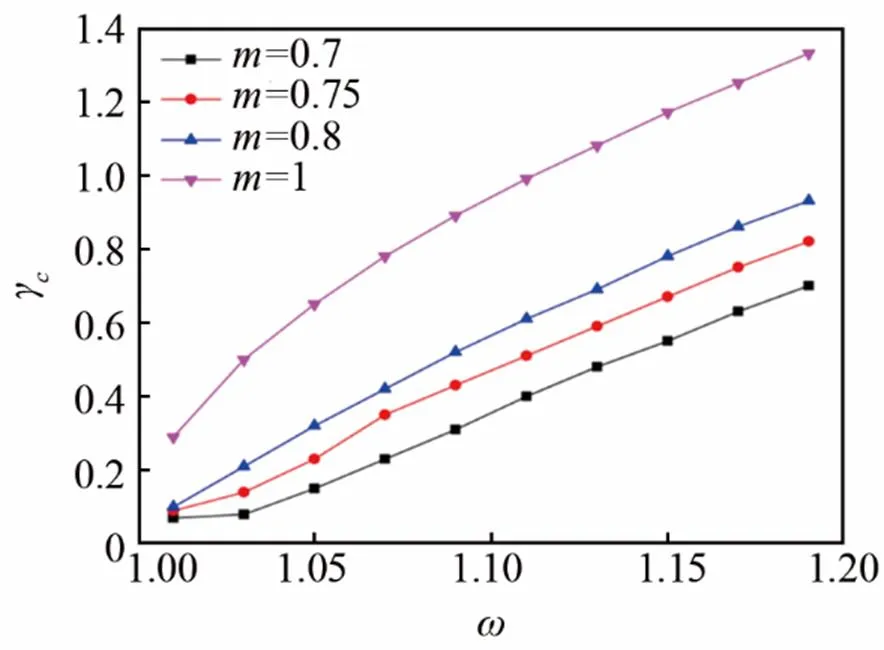
(a)-FPU链模型中临界驱动强度随驱动频率变化
(b) 耦合摆模型中临界驱动强度随驱动频率变化
图4-FPU链模型与耦合摆模型中临界驱动强度随驱动频率变化
Fig.4 Change of driving intensity threshold with driving frequency var-iation in-FPU chain model and coupling pendulums model
2.4 孤子释放周期的调控
孤子释放周期受到驱动强度、驱动频率的调制,并与缺陷处阻尼大小相关。驱动强度对孤子释放周期的调制在文献[10]中已经做过研究,本文在新模型中重复该结论以证明新模型的合理性。缺陷处阻尼对于孤子的激发有重要的影响,文献[10]中并未给出缺陷处阻尼对孤子释放周期的影响,本文旨在提出一种实验中可行的物理模型,因而对阻尼的作用作出更进一步的分析,从而为进一步的实验设计提供依据。
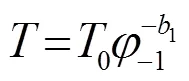
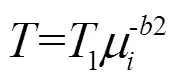
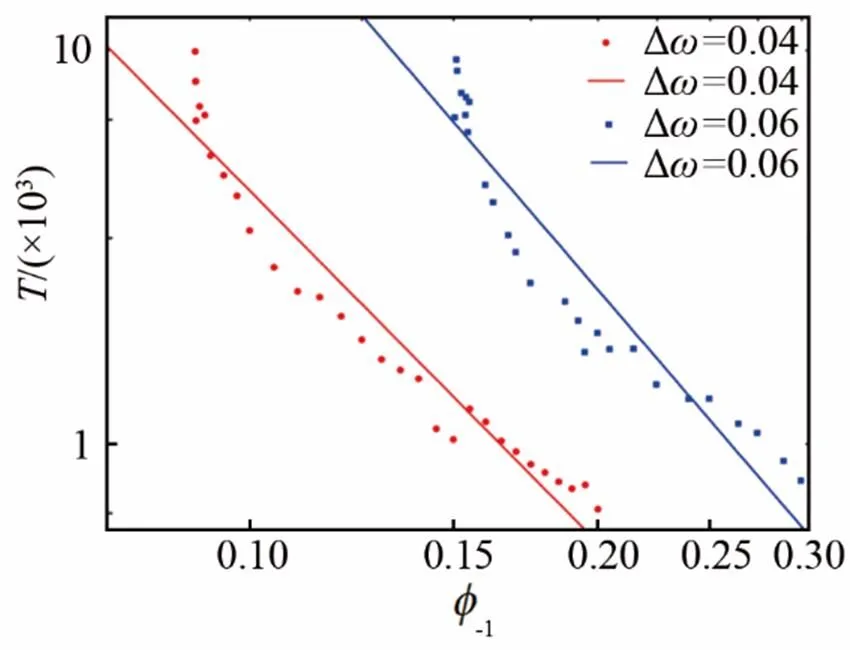
(a) 孤子平均激发周期随驱动强度-1变化
(b) 孤子平均激发周期随缺陷处阻尼系数μ变化
图5 孤子平均激发周期随驱动强度-1与缺陷处阻尼系数μ变化
Fig.5 Average emission periodversus driving intensity-1and damping coefficient of the impurity
3 结论
本文提出一种实验上实现孤子局域共振激发的简易可行的物理模型,并进行了理论分析和大量的数值模拟。理论分析与数值模拟证明,该方案在实验上实现局域共振激发孤子是切实可行的。然而,该模型与理想的-FPU链还有一些差异:(1) 该结构激发孤子需要的临界驱动幅值相较理想的-FPU链略低;(2) 同样驱动条件下,该结构释放孤子的周期更短。
数值模拟表明,随着缺陷处阻尼系数增大,孤子的幅度与宽度均减小,孤子的平均激发周期减小。这为该模型在实验上实现-FPU链孤子局域共振激发提供了理论依据。关于进一步的实验研究,我们会在以后的工作中给出。
[1] Trines R, Bingham R, Dunlop M W, et al. Spontaneous generation of self-organized solitary wave structures at Earth’s magnetopause[J]. Physical Review Letters, 2007, 99(20): 205006-205009.
[2] Farmer D, Armi L. The generation and trapping of solitary waves over topography[J]. Science, 1999, 283(5399): 188-190.
[3] Reznik G M, Zeitlin V. Resonant excitation of rossby waves in the equatorial waveguide and their nonlinear evolution[J]. Physical Review Letters, 2006, 96(3): 034502-034505.
[4] Georgiev D, Papaioannou S N, Glazebrook J F. Neuronic system inside neurons: molecular biology and biophysics of neuronal microtubules[J]. Biomedical Reviews, 2004, 2004(15): 67-75.
[5] Geniet F, Leon J. Energy transmission in the forbidden band gap of a nonlinear chain[J]. Physical Review Letters, 2002, 89(13): 134102-134105.
[6] Geniet F, Leon J. Nonlinear supratransmission[J]. Journal of Physics: Condensed Matter, 2003, 2003(15): 2933-2948.
[7] Leon J. Nonlinear supratransmission as a fundamental instability[J]. Physics Letter A, 2003, (319): 130-135.
[8] YU G, WANG X, TAO Z. Resonant emission of solitons from impurity-induced localized waves in nonlinear lattices[J]. Physical Review E, 2011, 83(2): 026605-026612.
[9] Khomeriki R. Nonlinear band gap transmission in optical waveguide arrays[J]. Physical Review Letters, 2004, 92(6): 063905-063908.
[10] Yamgoué S B, Morfu S, Marquié P. Noise effects on gap wave propagation in a nonlinear discrete LC transmission line[J]. Physical Review E, 2007, 75(3): 036211-036217.
[11] Koon K T V, Leon J, Marquie P, et al. Cutoff solitons and bistability of the discrete inductance-capacitance electrical line: theory and experiments[J]. Physical Review E, 2007, 75(6): 066604-06611.
[12] CHEN W Z. Experimental observation of solitons in a 1D nonlinear lattice[J]. Physical Review B, 1994, 49(21): 15063-15066.
[13] 朱逸斐, 陈伟中, 吕镭. 晶格模型中缺陷与孤波相互作用的实验观测[J]. 中国科学(G辑), 2003, 33(2): 97-102. ZHU Yifei, CHEN Weizhong, LÜ Lei. Experimental observation of solitons interaction with impurity in lattice model[J]. Science in China(Series G), 2003, 33(2): 97-102.
[14] Geniet F, Leon J. Energy transmission in the forbidden band gap of a nonlinear chain[J]. Physical Review Letters, 2002, 89(13): 134102-134105.
[15] ZHU C, LEI J, WU Y, et al. Experimental observation of solitary waves in a new designed pendulum Chain System[J]. European Jounal of Physics, 2015, 36(4): 045002-045011.
[16] Remoissenet M 1996 Waves Called Solitons: Concepts and Experiments[M]. Berlin: Springer, 1996: 212-213.
[17] 普朗特L, 奥斯瓦提奇K, 维格哈特K. 流体力学概论[M]. 郭永怀, 陆士嘉, 译. 北京: 科技出版社, 1981: 280-292. Prandtl L, Oswatitsch K, Wieghardt K.Führer durch die strömungs-lehre[M]. GUO Yonghuai , LU Shijia, Tranalate. Beijing: Science Press, 1981: 280-292.
[18] 郭保霞. 轴承基础知识[M]. 郑州:河南人民出版社, 2006: 188-201.
[19] 王卫华, 李明水, 陈忻. 斜拉索的阻力系数研究[J]. 空气动力学学报, 2005, 23(3): 390-393. WANG Weihua, LI Mingshui, CHEN Xin. Investigation on drag coefficients of stay cables[J]. Acta Aerodynamica Sinica, 2005, 23(3): 389-393.
A new physical model for the localized resonant emission of solitons
WANG Shao-hua1, LIU Hao-hua1, SHEN Yue-long2
(1. Key Laboratory of Modern Acoustic, Nanjing University, Nanjing 210093, Jiangsu, China;2. Information Science and Engineering College, Ocean University of China, Qingdao 266100, Shandong, China)
As one of the major field of nonlinear science, solitons have gotten lots of attention academically since they are discovered. However, although theories on their properties have been sufficient and mature, study on creation of solitons is still incomplete. Thorough research on creation of solitons is not only fundamental to understanding solitonic phenomena occurring in nature and physical systems, but also important to engineering applications of solitons. For those reasons, plenty of researches on approaches to solitons emission have been proposed continually. For an improvement upon the methods based on the energy supra-transmission in band gaps of nonlinear lattices, the so-called resonant emission method is proposed. According to this method, mechanism of local resonation is applied by introducing impurity in a semi-infinite-FPU chain. By doing this, the new methodnot only reduces drive amplitude that is needed to induce soliton emission dramatically, but also make solitons emission manageable. Althoughtheoretical analysis and numerical calculation have proved the method’s feasibility, experimental verification is not proposed. To push the theory further forward to experiment, we proved a feasible experimental scheme with simple physical model, and operated thorough theoretical analysis and numerical investigation.The new model is consist of simple linear springs, and realizes the β-FPU chain by designing the geometrical nonlinearity of the structure intelligently. The numerical investigations in our work have not only confirmed the feasibility of the scheme, but also have studied the special relationship between the duration of soliton emission and the driving amplitude and frequency. The results are consistent with the conclusion from the fore-mentioned paper. In addition, to provide reference for further experiments, we studied the special relationship between the duration of solitonemission and the damping on impurity union, as well as the influence of unions’ inhomogeneity on the emission and propagation of solitons.
soliton;-FPU chain; localized resonant; coupling pendulum
O322
A
1000-3630(2017)-03-0197-06
10.16300/j.cnki.1000-3630.2017.03.001
2016-10-18;
2017-02-02
国家自然科学基金资助项目(11174140)、国家973项目(2013CB632904)
王少华(1988-), 男, 河南三门峡人, 硕士研究生, 研究方向为非线性周期结构中的孤子。
王少华, E-mail: shitoucheng_w@sina.com

