混凝土表面开口裂缝对近表面声波影响
王鹏,韩庆邦,姜学平,郑豪,许洲琛
混凝土表面开口裂缝对近表面声波影响
王鹏,韩庆邦,姜学平,郑豪,许洲琛
(河海大学物联网工程学院,江苏常州,213022)
基于混凝土近表面不同波型的声速,分析开口裂缝对声波的影响。有限元仿真结果表明,激励源辐射的初始纵波经裂缝端点衍射产生纵波-与横波-,-以一定的角度射向混凝土表面经模式转换产生纵波--;初始横波在裂缝端点衍射产生纵波-与横波-;初始瑞利波在裂缝端点衍射后除了产生纵波-与横波-外继续沿着固体表面传播(-)。在此基础上,基于变型波到达接收阵元的时刻定量检测裂缝的深度,检测结果较单面平测法具有更高的信噪比与检测精度,可辅助单面平测法更精确地定量检测混凝土开口裂缝的深度。
无损检测;开口裂缝;混凝土
0 引言
随着现代社会的快速发展,对大体积大跨度混凝土构建(高速公路、桥梁、坝体)的需求越来越大。这些结构往往体积庞大,要求使用寿命长。而受温度骤变、自身体积变形、水分蒸发、不均匀沉陷以及施工条件等的影响,在混凝土表面很容易形成不同深度的裂缝,对建筑物伤害很大。因此有必要对这些裂缝进行检测,掌握其宽度深度等参数以判断裂缝对建筑物的损伤及寿命的影向。超声法检测混凝土具有许多其他无损检测方法所没有的优势,如穿透性良好、操作方便、价格低廉、检测精确度高等。超声检测混凝土表面开口裂缝深度的常用方法有:(1)单面平测法[1];(2)钻孔法;(3)瑞利波法[2-4]。钻孔法属破坏性检测,代价高昂,应用有限;基于纵波的单面平测法能准确地定量检测混凝土表面开口裂缝的深度,一般最大检测深度是500 mm;相比体波,瑞利波检测混凝土表面开口裂缝的优势,主要在于能量更大且不受流体的影响,潜在探测深度更高。
国内外学者在开口裂缝对声波的影响方面做了很多有价值的研究。Foo Wei Lee[2]等人使用中心能量匹配滤波法(Matched Filtering of Center of Energy,MFCE)确定了瑞利波的到达时刻,能从探头接收的复杂信号中有效提取出瑞利波。张在东[3]等人数值模拟了钢表面开口斜裂缝对瑞利波的影响,模拟结果表明瑞利波在到达裂缝处会分成两个部分,第一部分绕过裂缝尖端,第二部分沿着钢表面(包括裂缝)传播。G Hevin[5]等人发现频谱比的截止频率可以判断裂缝深度,仿真结果表明判断裂缝深度误差率不超过15%。杨洋[6]等人将时间反转法应用到检测混凝土表面开口裂缝深度中,发现混凝土表面裂缝越深,与表面波波长越接近,重构波形与激励波形差异越大,其损伤指数越高。Baskaran G[7]等人利用衍射时差法(Time of Flight Diffraction,TOFD)中的变型波(Shear-wave Time of Flight Diffraction,S-TOFD)进行检测,发现S-TOFD能够有效检测固体近表面的缺陷,增大了检测区域,提高了检测精度。
针对混凝土内部声场复杂的特点,本文基于混凝土近表面声波的波速来研究开口裂缝对近表面声波的影响,并进行有限元仿真验证。仿真结果显示,能清楚地分辨接收阵元接收的声波类型,判断它们的传播路径。此外,本文利用对裂缝端点处由模式转换衍生的变型波(横波或纵波)进行裂缝深度定量检测,发现变型波法检测精度高于单面平测法,变型波检测所用波型的信噪比高于单面平测法所用的波型。另外,变型波检测可结合平行扫查[8],减小衍射点不在两探头中线带来的误差,大幅度提高了检测精度。
1 裂缝对表面声波的影响
混凝土表面上传播的表面声波有:纵波、横波和瑞利波。其中纵波的波速最大,瑞利波波速与横波波速约为的一半。与的比值跟材料泊松比有很大关系。当混凝土的泊松比=0.33时,瑞利波波速约为横波的0.93倍。

图1 混凝土近表面声波传播示意图
根据混凝土近表面声波的波速,分析几何体中声波的传播规律如图1所示,图中、、分别表示纵波、横波及瑞利波;为激励源,为接收点,为裂纹端点,为裂纹根部;圆圈表示衍射,其中黑色表示衍射纵波,红色表示衍射横波。根据文献[7],固体近表面声波经裂缝端点的表现主要有,激励源辐射的初始纵波在裂缝端点衍射,经模式转换产生衍射纵波-与横波-,到达接收点;相似地,激励源辐射的初始横波在裂缝端点衍射,经模式转换产生衍射纵波-与横波-,到达接收点;能量最大的瑞利波在裂缝端点衍射,产生衍射纵波-、横波-以及继续沿着固体表面传播的瑞利波-。需要注意的是,如果激励源与接收点对称地放置在衍射点的两边,-与-到达接收点的时刻相同,两者叠加在一起。根据以上分析,可得出各声波到达接收阵元的声时为
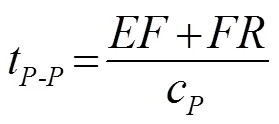
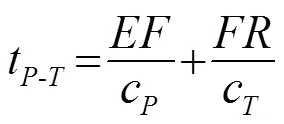
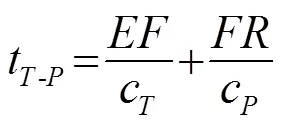
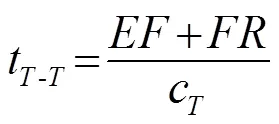
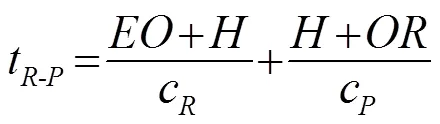
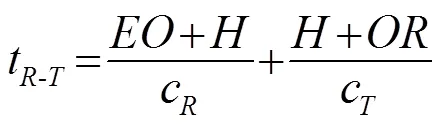
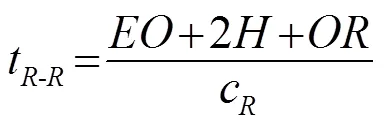
式(1)~(7)中:表示裂纹的长度;线段表示从点到点的声程;线段表示从点到接收阵元的声程;线段表示从点到点的声程;线段表示从点到接收阵元的声程。
2 有限元仿真与结果分析
2.1 有限元建模
宏观上,混凝土由砂、骨料、水等按一定比例配合搅拌而成,属各向异性介质。而本文从微观上探究界面处声波的传播规律,仅包括体波与面波,因此可将混凝土简化为各向同性介质。
本文采用有限元算法,仿真二维半无限混凝土界面处声波的传播规律。模型几何如图2所示,长宽分别为:600、200 mm,内部填充材质为混凝土,材料参数见表1。由表1可知,混凝土中纵波声速、横波声速、瑞利波声速。网格最大尺寸为1.67 mm;时间步长为4.16×10-8 s;采样频率为50 MHz;施加激励为点声源。采用一发多收的方式,200 mm处激发,400、420、440、460、480 mm处接收,各接收阵元依次记为1、2、3、4、5,所设裂缝宽度为2 mm,深度分别为20、30、40、50、60、70、80 mm。

图2 有限元几何模型

表1 混凝土参数
现实中,混凝土表面与空气接触,由于两者声阻抗相差很大,接触边界可等效为自由边界[9]。模型中,上边界为自由边界(外部为真空),裂缝侧壁也为自由边界,其余边界均设置为吸收边界,防止声波经由边界反射干扰接收信号。由于近场效应,发射、接收传感器相距较小时,横波与瑞利波混在一起难以分辨,文献[4]指出,发射、接收传感器的距离不宜低于150 mm,本文选取200 mm。
2.2 裂缝对混凝土近表面声波的影响
裂缝深度为40 mm的模型仿真结果见图3,从图3中可清晰地观察初始激励纵波,初始激励横波,初始瑞利波,衍射纵波-、-、-,衍射横波-、-、-与瑞利波-的产生和传播。图4为1接收的声波信号,通过观察声场的变化,结合不同波型的声速可以判定依次到达1的波型分别是:
(1) 初始纵波经裂缝端点衍射而产生的纵波-;
(2) 初始纵波经裂缝端点衍射产生的横波,以一定的角度射向混凝土表面经模式转换产生的纵波--;
(3) 初始纵波在裂缝端点衍射产生的横波-与初始横纵在裂缝端点衍射产生的纵波-[7],两者同时到达接收阵元;
(4) 初始瑞利波沿着混凝土表面传播到裂缝端点,经衍射产生的纵波-;
(5) 初始横波经裂缝端点衍射产生的横波-;
(6) 瑞利波经裂缝端点衍射产生的横波-;
(7) 一直沿着固体表面传播的瑞利波-。
图5是1~5接收的声波信号,图中的斜线连接不同阵元接收相应声波的峰值:红线对应的波型为纵波;蓝线对应的波型为横波;黑线对应的波型为瑞利波。为了更准确地判定各声波的类型,基于各阵元的位置及其接收不同波型波峰的到达时刻,计算不同波型的声速,结果纵波的声速为4 013 m/s;横波的声速为2 021 m/s;瑞利波的声速为1 886 m/s,计算所得速度与材料中不同波型的声速吻合。

(a)40 μs
(b)63 μs
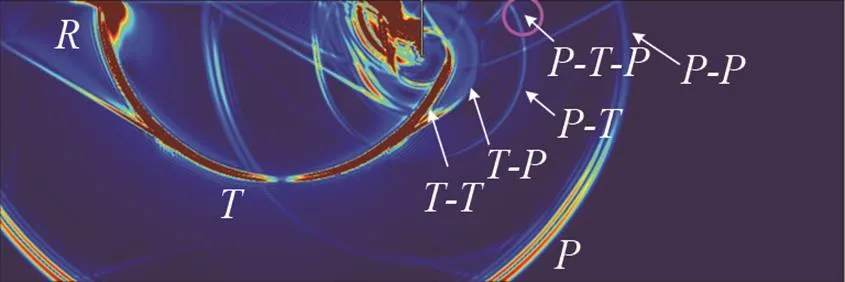
(c)66 μs
(d)85 μs
图3 不同时刻的声场
Fig.3 Ultrasonic fields at different moments
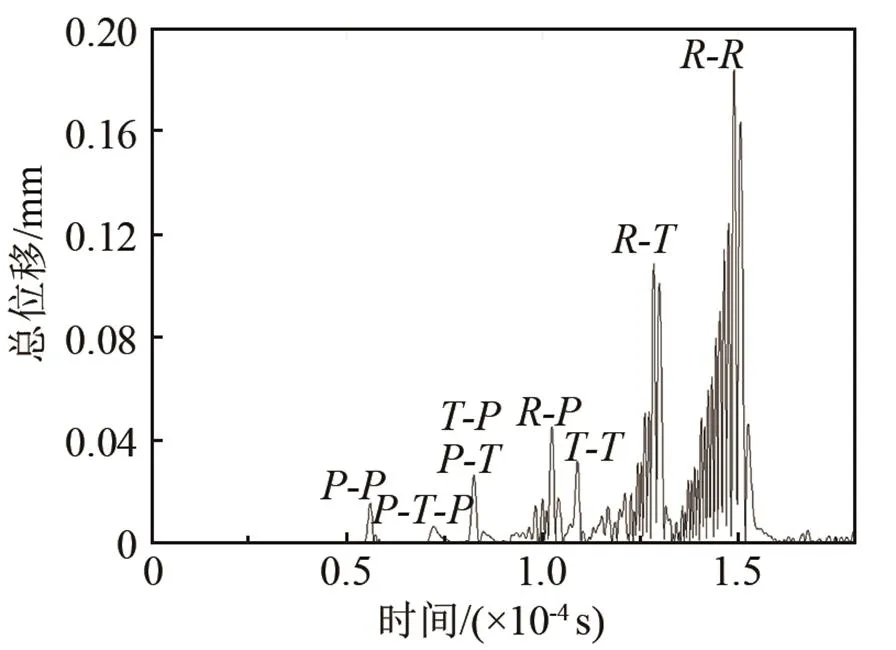
图4 R1接收的声波信号

图5 R1~R5接收的声波信号
2.3 混凝土表面裂缝的定量检测
在超声法检测混凝土规程中涉及的单面平测法中,检测混凝土开口裂缝深度所用的波型是图4中的-。将不同深度裂缝模型接收到-的声时代入式(8)可算得裂缝的深度[1]:
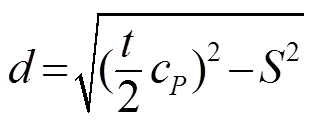
式中:为裂缝深度;为到达接收阵元的时刻;为激励与接收阵元距离的一半。计算结果如表2和图6所示。
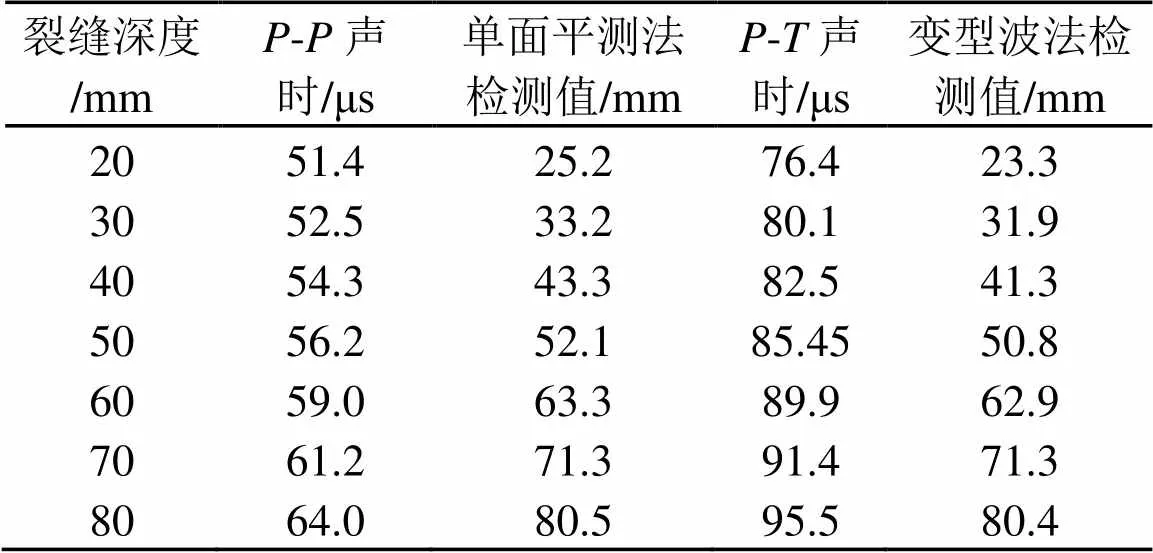
表2 单面平测法与变型波法检测裂缝深度值
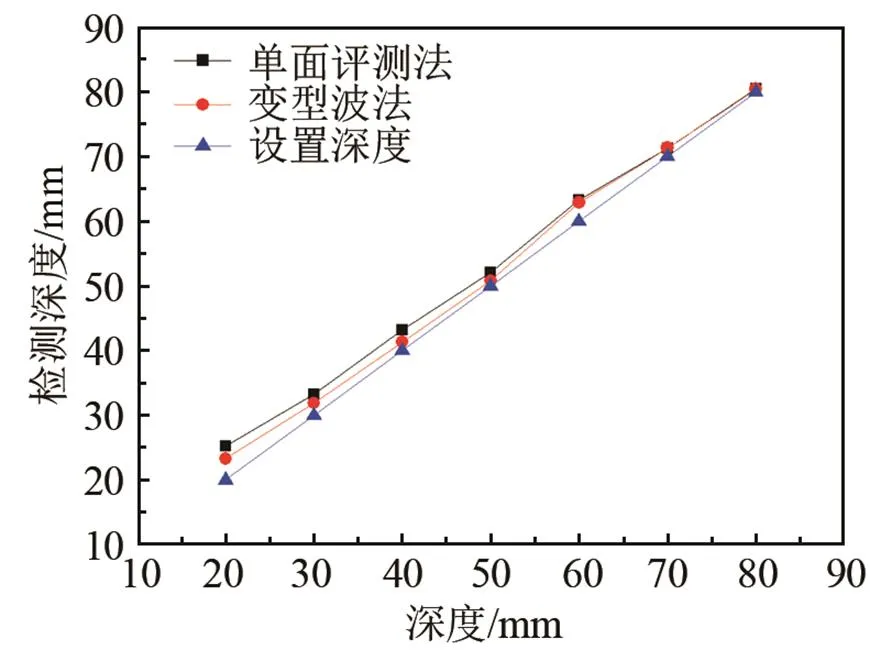
图6 单面平测法与变型波法检测的裂缝深度值
如果激励源与接收点对称放置在衍射点两边,-与-到达接收点的时刻相同。需要注意的是,如果激励源与接收点非对称放置在衍射点两边,裂缝深度的计算有误差。可通过绘制偏离衍射点的水平距离-变型波到达时间函数曲线,根据曲线之间的交点来计算衍射点的深度,能有效减小计算误差[8]。根据激励接收点的距离2、工件横波声速、纵波声速,混凝土表面裂缝深度值可由式(9)定量确定:
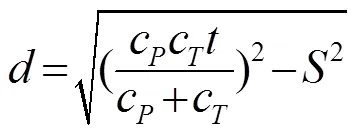
式中,是接收阵元接收-或者-的时刻。变型波法检测结果如表2和图6所示。
根据图6和表2中的数据可知,变型波法检测的裂缝深度误差小于单面平测法,检测精度高于单面平测法,原因在于变型波法所用的-波长小于单面平测法所用的-。另外,较单面平测法所用的纵波,变型波的信噪比更高。
3 结论
本文基于混凝土近表面声波的波速,分析了开口裂缝对近表面声波的影响,得出:激励源辐射的初始纵波经过裂缝端点产生衍射纵波-与横波-;激励源辐射的初始横波经过裂缝端点产生衍射纵波-与横波-;-在传播至接收点的过程中,会以一定的角度射向工件表面,经模式转换产生新的纵波--;瑞利波沿固体表面传播,在裂缝端点处衍射产生纵波-、横波-,随后瑞利波继续沿着固体表面传播(-)。
基于开口裂缝对近表面声波的影响,本文根据变型波-或-到达接收阵元的时刻来定量检测裂缝深度,变型波的波长小于纵波,因此变型波检测精度高于单面平测法,变型波检测所用的-(或-)信噪比也高于单面平测法所用的-。另外,变型波检测可结合平行扫查,有效减小衍射点不在两探头中线带来的误差,大幅度提高检测精度。
[1] 李俊如, 高建光, 王耀辉. 超声波检测混凝土裂缝及裂缝成因分析[J]. 岩土力学, 2001, 22(3): 291-293 LI Junru, GAO Jianguang, WANG Yaohui. Supersonic wave testing on concrete crack depth and analysis of crack initiation[J]. Rock and Soil Mechanics, 2001, 22(3): 291-293.
[2] LEE Foowei, CHAI Hwakian, LIM Koksing. Assessment of reinforced concrete surface breaking crack using rayleigh wave measurement[J]. Sensors, 2016, 16(3): 337-358.
[3] 张在东, 卢超, 魏运飞. 表面开口裂缝超声表面波频谱法测量的数值模拟[J]. 无损检测, 2009, 31(12): 993-997. ZHANG Zaidong, LU Chao, WEI Yunfei. Numeircal simulation to sizing surface-breaking cracks by ultrasonic surface wave spectral methed[J]. Nondestructive Testing, 2009, 31(12): 993-997.
[4] 冯若愚, 陈瑛, 李志双. R波谱能量透射比法检测大体积混凝土裂缝研究[J]. 振动与冲击, 2016, 35(12): 221-225. FENG Ruoyu, CHEN Ying, LI Zhishuang. Cracks identification of mass concrete structures with R wave spectral energy transmission ratio method[J]. Journal of Vibration and Shock, 2016, 35 (12): 221-225.
[5] Hevin G, Abraham O, Pedersen H A, et al. Characterization of surface cracks with Rayleigh waves: a numerical model[J]. NDT & E International, 1998, 31(4): 289-297.
[6] 杨洋, 张梦阳, 肖黎, 等. 表面波时间反转混凝土梁裂缝损伤识别数值模拟[J]. 混凝土, 2015, 13(12): 17-20. YANG Yang, ZHANG Mengyang, XIAO Li, et al. Simulation study of surface breaking crack in concrete beam based on time- reversed theory of surface wave[J]. Concrete, 2015, 13(12): 17-20.
[7] Baskaran G, Balasubramaniam K, Rao C L. Shear-wave time of flight diffraction (S-TOFD) technique[J]. NDT & E International, 2006, 39(6): 458-467.
[8] 张东辉, 刘丽丽, 张树潇, 等. TOFD检测平行扫查中变型波的识别与应用[J]. 无损检测, 2015, 37(7): 54-56. ZHANG Donghui, LIU Lili, ZHANG Shuxiao, et al. Identification and utilization of transformed wave in TOFD parallel scanning[J]. Nondestructive Testing, 2015, 37(7): 54-56.
[9] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 3版. 南京: 南京大学出版社, 2001. DU Gonghuan, ZHU Zhemin, GONG Xiufen. Fundamental acoustics[M]. 3rd edition. Nanjing: Nanjing University Press, 2001.
The influence of surface opening cracks on the sound wave near concrete surface
WANG Peng, HAN Qing-bang, JIANG Xue-ping, ZHENG Hao, XU Zhou-chen
(College of Interhet of Things Engineering, Hohai University, Changzhou 213022, Jiangsu, China)
Based on the velocities of different wave modes near concrete surface, the influences of surface-crack on these wave modes are analyzed. Finite Element Method (FEM) simulation results show that the original longitudinal waveis diffracted at crack tip togenerate longitudinal wave-and transverse wave-, and the latter propagates onto surface with a certain angle of incidence to result in a new longitudinal wave--; the original transverse waveis diffracted at crack tip togenerate longitudinal waveand transverse wave-;the original Rayleigh waveis diffracted at crack tip to generate longitudinal waveand transverse wave-, and continues to propagatealong the solid surface (-). On the basis of the simulation results, the multi-mode wave method by measuring the arrival times of variant waves to receiver can be utilized to measure the depth of surface crack with higher signal-to-noise ratio and more precise resolution compared to the single plane method.
nondestructive testing; surface-crack; concrete
TB556
A
1000-3630(2017)-03-0247-05
10.16300/j.cnki.1000-3630.2017.03.009
2016-12-02;
2017-04-01
国家自然科学基金资助项目(11274091、11574072)、江苏省重点研发计划(BE2016056)、河海大学中央高校基金项目(2011B11014)、河海大学中央高校基本科研业务费资助项目(2016B48814)
王鹏(1993-), 男, 江苏宿迁人, 硕士研究生, 研究方向为通信与信息系统。
韩庆邦, E-mail: hqb0092@163.com

