应用改进Stearns-Noeche模型的色纺纱配色技术

王玉娟， 马崇启， 刘建勇， 程 璐， 张红梅， 王 宣

(1. 天津工业大学 纺织学院， 天津 300387； 2. 山东如意科技集团， 山东 济宁 272100)

应用改进Stearns-Noeche模型的色纺纱配色技术

王玉娟1， 马崇启1， 刘建勇1， 程 璐1， 张红梅2， 王 宣2

(1. 天津工业大学 纺织学院， 天津 300387； 2. 山东如意科技集团， 山东 济宁 272100)

针对传统的人工配色繁复、效率低而现有的计算机配色修色算法不能满足生产实践需求的问题，在MatLab软件中开发出了一套计算机辅助色纺纱配色系统，并对该系统中的配色模块和修色模块进行了改进。在配色模块，采用在[0 1]区间对未知参数M值和对单色纤维初始配方赋值迭代的方法，改进了采用M值平均数的方法以及基于最小二乘法的初始配方求解算法；在修色模块，采用单色纤维调整量中间函数差最小的方法，改进了基于最小二乘法的三刺激值或反射率修色算法。该模型经过1～2次修色可得到色差小于1的配色结果，能满足色纺纱生产中多组分、定比例的配色、修色基本要求。

色纺纱； Stearns-Noeche模型； 配色技术； 计算机配色系统

色纺纱起步于黑色涤纶与棉混纺的麻灰纱[1]，具有立体、朦胧、时尚等风格特点，深受企业和消费者欢迎。色纺纱市场在逐年扩大，前景非常可观。又因其工艺是先对纤维染色然后进行纺纱，因此大大减少了纺织用水，具有环保、经济的特点[2]。除此之外，色纺纱具有小批量、多品种、快交货的特点，因而如何快速、准确的打样，已成为色纺企业发展的关键。而打样的核心在于配色，传统的配色技术主要依赖人工经验，局限性较大，且影响因素较多，效率较低[3]。国内一些学者已对此进行了研究，主要对Stearns-Noeche模型算法、Friele模型算法、Kubelka-Munk双常数/单常数模型算法[4-5]，以及BP神经网络算法[6]进行改进。Kubelka-Munk双常数/单常数理论，计算有颜色梯度的色纺纱时，效果较好；BP神经网络算法，配色结果与样本容量大小有较大关系。Stearns-Noeche算法和Friele算法中都有未知参数，之前的学者大都采用提前纺纱[7]，计算未知参数，然后求其平均值，工作量大，且未知参数的平均值使运算不能具体化，对于不同的色纺纱配方预测时，存在误差。本文通过改进Stearns-Noeche算法中未知参数M值的确定方法、初始配方的计算方法，寻求一种更加适用于生产实践、配色效率更高的计算机配色算法。

1 Stearns-Noechel 模型

纤维的混合只是物理混合，理论上应该有某种加和关系存在，假设存在中间函数f[R(λ)]，有

(1)

1944年，Stearns和Noechel通过实验得出经验公式，称之为Stearns-Noeche模型，公式如下：

(2)

式中：M为一可变常量；f[r(λ)]是反射率r(λ)关于波长λ的中间函数。

由式(2)可反推出反射率r(λ)和中间函数f[r(λ)]之间的关系为

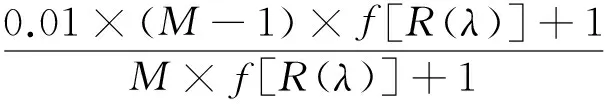
(3)

在已知参数M值，单色纤维的反射率r(λ)时，可利用式(2)计算出单色纤维的中间函数f[r(λ)]。又已知单色纤维的混色比例x时，可利用式(1)计算出混色纤维的中间函数f[R(λ)]。此时，再利用公式(3)即可求得混色纤维的拟合反射率Rbat(λ)，此后可利用色差公式求解混色样拟合反射率Rbat(λ)与标样反射率Rstd(λ)之间的拟合色差以及其他色度参数。

本文基于该算法在MatLab软件中编写一套色纺纱配色软件，该软件包括配色和修色2个大主要模块。

2 配色模块

在对某个标样进行配色时，首先要选择单色样，对于如何选择的问题，应有一个大概的了解。在选择完单色后，就可利用配色算法进行配色。而配色算法中的核心环节是未知参数M值的求解，以及单色纤维初始配方的求解，前人对此进行了大量研究，笔者在分析试用前人的算法后，对此算法进行了改进。

2.1 单色的选择

在选择单色时，标样中的每种颜色一般选择 2～3 个单色，因此一个含2种颜色的标准样一般选择4～6个单色进行配色。

由于计算机配色可能出现“同谱异色”的现象，即拟合配方所得的拟合反射率与标样的反射率非常接近，理论上以此拟合配方纺出的试样应该与标样颜色一样，但是会出现风格的差异，例如标样是夹花风格，而纺样是素面风格。针对此问题，目前尚没有有效的解决方法，只能在配色之前，仔细观察标样，结合自身经验对标样中有哪些单色纤维进行确定。如果单色选择偏差较大，配色结果也将出现较大误差，因此，选择单色是计算机配色的第1步，也是非常重要的一步。然而在积累较多配色结果之后，计算机可根据标样的颜色，给出参考单色，以此减去对配色人员经验的依赖程度。

2.2 未知参数M值的计算方法

在式(2)中，只有一个未知参数M，M值与单色纤维的种类、颜色以及在其混色样中的比例有关。之前许多学者试图通过求M值的平均数来固定某种纤维的未知参数M值，结果如表1所示。

本文利用博拉彩虹纤维有限公司提供的红色、黄色、蓝色、黑色、白色、靛蓝色、卡其色、宝石蓝色、翠绿色、灰色、枣红色粘胶纤维，按照一定的混色比，进行两色或三色混合，得到132个混色样，分别求解每个混色样的最佳参数M值。求解方法如图1所示。

表1 不同纤维在Stearns-Noeche配色模型中的参数M值Tab.1 Parameter M value of different fibers in Stearns-Noeche color matching model

图1 最佳参数M值计算方法Fig.1 Calculation method of optimal parameter M value

在求混色样最佳参数M值时，混色样中单色纤维以及单色纤维的质量比已知，只需为参数M赋值，即可根据前文中描述的方法计算出拟合反射率。然后再用CMC色差计算公式计算色差。当拟合反射率与标样反射率之间的拟合色差最小时，即认为此事的参数M值是该试样的最佳参数值；而在色差没有达到最小时，可通过改变对M值的赋值继续计算，直至求出色差最小时的M值。

图2示出132个混色试样的最佳M值分布情况。由图可看出，每个试样的最佳M值都是不一样的。如果采取M值固定为某一个数值，例如所有最佳M值的平均数，那么在对某个试样进行配色时，当固定的M值比较接近该试样最佳M值时，拟合配方会较好，但是如果与该试样最佳M值相差较大，则拟合配方就会较差。如果使用不同种类的纤维配色时，需要提前混纺一些试样来求该种纤维的最佳M值，即使用同种纤维混色，例如涤纶，也不能采用前人总结出来的最佳参数M值，仍需重新打样求解，除多品种外，色纺企业还经常生产混纺纱，又需从新打样求解混纺纱的M值，因此前期工作量大而繁琐。由于不同种类的纤维纯纺或混纺，其参数M值都在0～1之间取值，因此本文采取在区间[0 1]对参数M值赋值迭代的方法，在MatLab环境中，编写基于Stearns-Noeche模型的配色模块。

图2 所有混色样的最优参数M值Fig.2 Optimal parameter M value of all samples

2.3 单色纤维初始配方计算方法

之前有许多学者使用基于最小二乘法的全光谱配色算法[13-14]，但是这种算法在计算混色样配方时，有时会出现该混色样中的某些单色样的拟合配方为负值的情况，例如对以下混色样进行配色(这些混色样的反射率以及所用单色纤维的反射率如表2所示)时，采用M在[0 1]区间迭代结合最小二乘法对该色样进行配色，得到的拟合配方与M值的关系如图3所示。

表2 混色样及单色纤维的反射率Tab.2 Reflection of blended and monochrome fibers %

图3 各单色纤维配方拟合值与参数M值的关系Fig.3 Relationship between monochrome fiber and parameter M

由图3可看出，无论M如何取值，得到单色纤维C的拟合配方为负值，而负的拟合配方是没有实用意义。除此之外，利用最小二乘法求拟合配方并不能满足企业的配方计算要求，因为色纺企业收到的客户订单，大都为多组分混色样，例如涤/棉(65/35)，即使是单组分的混色样，也有要求使用精梳纤维、普梳纤维等混纺的。本文采用对单色样配方赋值的方法进行计算，这种方法不会出现配方为负值的情况，并可满足企业“多组分、定比例”的配色要求。

2.4 配色模块计算流程

基于以上M值的计算方法和单色纤维初始配方的求解方法，改进后配色模块的计算过程如图4所示。

图4 配色模块计算过程Fig.4 Calculation process of matching color model

利用该配色模块对标样进行配色时，首先要测试出标样的反射率，用于后续配色；其次要仔细观察标样中有哪些颜色，然后根据经验选择单色纤维并测试出单色纤维的反射率。然后根据小节1，可以计算出拟合反射率。通过色差公式计算出标样反射率和拟合反射率之间的拟合色差，如果色差满足要求，则可输出此时单色纤维的混色质量比以及相应的M值；如果色差不满足要求，则重新对M值以及单色纤维混色质量比赋值，直至色差满足要求为止。

整个计算过程的核心部分是对单色纤维混色质量比赋值环节。如果是普通的纯纺色纺纱，那么赋值环节比较简单，只需要满足各种单色纤维质量比加和为1；如果是混纺纱，例如涤/棉(65/35)，那么赋值环节不仅要满足各种单色纤维质量比加和为1，还需要满足棉纤维质量比加和为0.65，涤纶纤维质量比加和为0.35的要求。而纯纺中也会出现质量比要求，例如要求精梳棉和普梳棉质量各占多少比例的色纺纱，其配色方法与混纺纱类似。

3 修色模块

无论配色模块给出的拟合配方如何接近混色样的真实配方，在打样过程中总会存在操作误差、机器误差，也会由于环境等因素的变化造成误差，因此纺出的小样总会与标样存在色差。在色差较大，不能满足生产要求时，就需要对小样进行修色。之前学者使用的修色方法有反射率修色法和三刺激值修色法，具体算法可参考文献[7]，但在使用该算法进行修色时，修色结果并不理想，而且这种修色算法不能满足“多组分、定比例”混色样的修色要求，所以本文对修色模块也进行了改进。

修色模块的改进思想仍然从赋值循环的程序编写思想出发，改进后的修色模块计算过程如图5所示。

图5 修色模块计算过程Fig.5 Calculation process of color repairing model

修色时，采用单色纤维调整量中间函数差最小的方法。首先要测试小样的反射率，然后对参数M进行赋值，根据式(2)将小样和标样的反射率都计算成相应的中间函数，并计算其差值△f[R(λ)]。接着对单色纤维需要调整的质量比进行赋值，然后将相应的单色纤维的调整量类似看作式(1)中各单色纤维的质量比，得到由单色纤维调整量计算出来的拟合中间函数△f[r(λ)]。当△f[R(λ)]和 △f[r(λ)]之差最小时，输出此时单色纤维相应的调整量，再与之前小样的配方相加，即可得到修正后的配方。如果△f[R(λ)]和△f[r(λ)]之差不是最小，那么就重新对M值和单色纤维调整量赋值，直至△f[R(λ)]和△f[r(λ)]之差最小为止。

在对单色纤维调整量赋值时，要保证同组份、同要求的各单色纤维调整量加和为0。

4 色纺纱计算机配色系统

在配色模块和修色模块都编写完成后，整个计算机配色软件的核心部分完成，大致流程如图6所示。基于配色软件，搭配一些测色仪、电脑、打印机等设备，就得到了一套计算机辅助的半智能配色系统(因为选色环节还需依靠人工进行)。

图6 计算机配色流程Fig.6 Process of computer matching color

5 实验验证

利用该套配色系统，对一浅红色试样进行配色实践，分别采用粘胶纯纺以及棉/粘胶(60/40)混纺的方法进行配色，通过观察待配试样，选取几种不同颜色的棉和粘胶纤维。待配试样和所选单色的反射率值如表3所示。其中只有单色纤维H是棉纤维，其他均为粘胶纤维。

表3 混色样及单色纤维的反射率Tab.3 Rreflection of blended and monochrome fibers %

5.1 测色过程

本文所用测色仪为Datacolor公司的Datacolor SF600。选取大孔径、包含镜面光泽、100%UV(滤镜off)的测色条件，以及D65、10°视角的观察条件，分别对纱线板正反面进行横向和垂直2个方向、不同部位进行测色，直至最终颜色偏差小于0.1，记录下该色样的反射率值(360～700 nm，间隔10 nm)。

5.2 配色结果与分析

配色结果如表4所示。由表中配色结果可看出，经过1～2次修色，即可配出与标样色差小于1的纺样，配色效率较高，可满足色纺纱配色的基本需求。

表4 配色结果Tab.4 Matching color results

本文实验测试时采用的是Datacolor接触式测色仪，该测色仪测色时要求试样要足够厚，不透光，而生产中的客户来样有时很小，这种情况下建议采用非接触式的Digeye测色仪进行测色。

6 结 论

利用Stearns-Noeche模型对色纺纱进行配色，通过改进Stearns-Noeche模型中未知参数M值的确定方法，打破了之前固定M值配色的模式，使每个试样配色时都能得到最佳的M值，不仅省去了为求M值而做的大量打样工作，还提高了配色的准确性。采用对单色样拟合配方赋值迭代的方法，避免了采用最小二乘法求配色时存在的缺陷，且更能满足生产多组分、定比例的纺纱要求。改进后的计算机配色系统，虽然还需要根据经验选取单色，但整体降低了对配色人员尤其是高级配色技术人员的依赖，修色次数较少，配色效率较高。

[1] 任安民, 周立明. 色纺纱配色方法改进初探[J]. 棉纺织技术, 2007, 35(6): 14-16.

REN Anmin, ZHOU Liming. A probe to the improvement of color matching method of colored spun yarn[J]. Cotton Textile Technology, 2007, 35(6): 14-16.

[2] 王成, 张峰, 姚里荣, 等. 载银粘胶色纺面料的制备及其抗菌性能[J]. 纺织学报, 2014, 35(1): 91-92.

WANG Cheng, ZHANG Feng, YAO Lirong, et al. Preparation and antimicrobial property of silver-loaded color spun rayon fabrics[J]. Journal of Textile Research, 2014, 35(1): 91-92.

[3] 金亚琪, 邹专勇, 许梦露, 等. 色纺纱产品开发现状及技术发展需求[J]. 棉纺织技术, 2012, 40(12): 65-68.

JIN Yaqi, ZHOU Zhuanyong, XU Menglu, et al. Development status and technology development demands of colored spun yarn[J]. Modern Textile Technology, 2012, 40(12): 65-68.

[4] VESNA D, ZELJKA B M, KATARINA I.Kubelkamunk theory in describing optical peoperties of paper[J]. Technical Gazette, 2011, 18(1): 117-124.

[5] PHILIPS-INVEMIZZ B, DUPONT D, CAZE C. Formulation of colored fiber blends from friele′s theoretical model[J]. Color Research and Application, 2001, 27(3): 191-198.

[6] 刘贵, 于伟东. 毛精纺前纺工艺参数重要性的BP网络定量评价法[J]. 纺织学报, 2008, 29(1): 35-36.

LIU Gui, YU Weidong. Quantitative evaluation method for the significance of worstedfore-spinning parameters based on BP neural network[J]. Journal of Textile Research, 2008, 29(1): 35-36.

[7] 许佳艳. 涤棉双组分纤维计算机辅助配色的研究[D]. 杭州: 浙江理工大学, 2013:1-30.

XU Jiayan. The study on computer aid matching of colored fiber blends of polyester and cotton[D]. Hangzhou: Zhejiang Sci-Tech University, 2013:1-30.

[8 ] DAVIDSON H R, TAYLOR M. Prediction of the color of fiber blends[J].Journal of the Optical Society of America,1965, 55(1): 96-100.

[9] BURLONE D A. Theoretical and practical aspects of selectedfiber-blend color formulation functions[J]. Color Research and Application, 1984, 9(4): 213-219.

[10] ASPLAOD J R, ZHOU M. Influence of blending on color appearance of black and whiter fiber blends[J]. Textile Chemist and Colorist and American Dyestuff Reporter, 2000, 32(10): 47-51.

[11] PHILIPS B，DUPONT D，JOLLY A, et al. Color formulation by fiber blending using the Stenras-Noechel model[J]. Color Research and Application, 2002, 27(2): 100-107.

[12] 李戎, 黄劲旭. 有色纤维配色的光谱配色算法[C]//上海印染新技术交流研讨会论集. 上海:[出版者不详], 2005: 303-305.

LI Rong, HUANG Jinxu. Spectrum color matching Algorithm of colored fiber matching color[C]//The Collection of the Printing New Technology Exchange Conference in Shanghai. Shanghai: [s.n.], 2005: 303-305.

[13] 沈加加, 张志强, 陈燕兵, 等. 基于Stearns-Noechel模型的混色毛条颜色预测[J]. 纺织学报, 2008, 29(11): 61-62.

SHEN Jiajia, ZHANG Zhiqiang, CHEN Yanbing, et al. Match prediction forblended-color wool tops based on Stearns-Noeche model[J]. Journal of Textile Research,2008, 29(11): 61-62.

[14] 沈加加, 陈维国, 周华. 一种色纺纱配色的配方筛选与修正方法: 中国, 201210173593[P]. 2012-10-24.

SHEN Jiajia, CHEN Weiguo, ZHOU Hua. A kind of method to chose and repair the formula of matching the colored fiber yarn: China, 201210173593[P]. 2012-10-24.

MatchingcolortechnologyofcolorblendedyarnbasedonmodifiedStearns-Noechemodel

WANG Yujuan1, MA Chongqi1, LIU Jianyong1, CHENG Lu1, ZHANG Hongmei2, WANG Xuan2

(1.SchoolofTextiles,TianjinPolytechnicUniversity,Tianjin300387,China;2.ShandongRuyiCottonTextileGroup,Jining,Shandong272100,China)

Aiming at the problem that conventional artificial color matching is complicated, and low in efficiency, and the existing computer color matching algorithm can not meet the needs of production practice. A computer-aided color matching system for colored fiber was developed in MatLab software, and the color matching module and the color repairing module of the system were improved. In the color matching module, the method of calculating the mean value of the M value and the initial recipe solution based on the least squares method were improved by using the method of assignment and iteration to the unknown valueMand the initial recipe of the monochromatic fiber in the [0 1] interval. In the repairing module, the tristimulus value or the reflectance color repairing algorithm based on the least squares method was improved by the method of minimizing the difference in the function of monochromatic fiber. The color matching model can achieve the matching result with color difference smaller than 1 after repairing color for 1-2 times, which can satisfy the basic requirements of the color matching and color repairing of multi-component and fixed proportion in the production process of colored fibers yarn.

color blended yarn; Stearns-Noeche model; matching color technology; computer matching color system

TS 114

A

10.13475/j.fzxb.20161103207

2016-11-14

2017-04-02

国家重点研发计划专题项目(2016YFB0302801-03)

王玉娟(1992—)，女，硕士生。主要研究方向为色纺纱计算机测配色技术。马崇启，通信作者，E-mail:tjmcq@tjpu.edu.cn。