混流汽车装配线缓存区配置优化

黄 鹏, 唐火红, 何其昌, 王 克

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.上海交通大学 机械与动力工程学院,上海 200240)

混流汽车装配线缓存区配置优化

黄 鹏1, 唐火红1, 何其昌2, 王 克1

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.上海交通大学 机械与动力工程学院,上海 200240)

混流汽车装配线工艺复杂,关键位置缓存区数量难以确定,造成装配线无法正常、高效运行。文章以评价混流汽车装配线重要因素的装配线平滑指数和产能最大化为优化目标,建立以混流汽车装配线工艺信息、空间布局、物流路径为约束条件,关键位置缓存区数量为变量的仿真模型;针对该问题的复杂性,提出了一种基于遗传算法的仿真优化算法,并在Delmia/QUEST仿真环境中进行仿真优化,从而确定关键位置缓存区最优数量,实现装配线动态平衡和产能最大化。

混流装配线;缓存区数量;遗传算法;仿真优化;动态平衡;产能最大化

随着制造业的迅速发展,我国制造业由传统的手工式生产方式向“智能制造”方向迅速发展[1]。将传统的制造模式与计算机技术相结合,利用计算机强大的计算仿真能力,解决传统制造模式中生产效率低、生产瓶颈位置难预测、资源分配不合理等问题,使得制造系统能够快速响应,迅速配置制造资源,合理规划生产线布局[2]。现有研究表明,在企业生产线和加工设备固定、加工工艺顺序不变的条件下,关键位置缓存区的数量将直接影响整条生产线的动态平衡和工作效率[3],而关于如何快速准确地配置生产线缓存区数量的研究则较少。

物流仿真具有可视化、实时性和全面性等优点[4]。如何利用仿真模型的优点,快速准确地得到装配线缓存区数量,是“智能制造”发展的一个重要环节。本文以某汽车装配车间混流装配线为例,提出了一种基于遗传算法的仿真优化算法,在Delmia/QUEST软件平台上参数化建立仿真模型,并对该装配线进行仿真试验;根据仿真优化试验得到缓存区的大小,并将优化结果运用到装配车间中,得到装配线工位利用率,通过与初始方案进行比较,验证了仿真优化算法的可行性和有效性。

1 工艺流程分析

该汽车装配线是典型的混流装配线,加工A、B、C 3种车型的汽车,其简化工艺流程如图1所示。

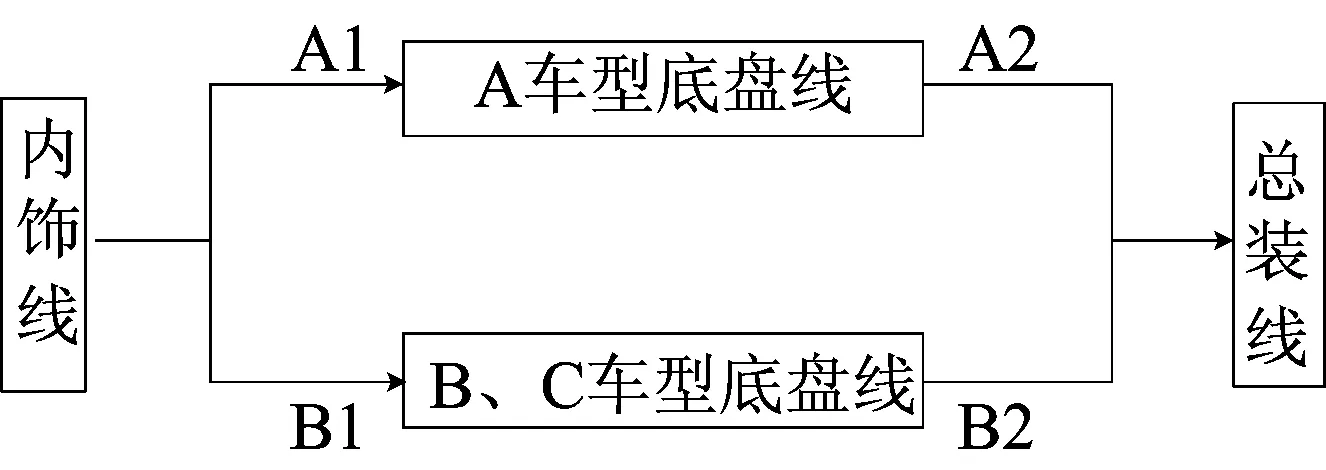
图1 简化的汽车装配线工艺流程

A、B、C 3种车型按照36∶32∶32的比例进入内饰线。3种车型的内饰线和总装线工艺是相同的,而底盘线加工采用分流加工的模式,装配线中A1、A2、B1、B2这4个位置缓存区的大小对装配线会造成很大的影响。若缓存区过大,则造成车间空间利用率变小,生产成本增加;若缓存区过小,则造成装配线物流堵塞,影响工位利用率,降低产能。由此可见,混流装配线关键位置缓存区的大小是装配线设计过程中很重要的一个环节,准确而高效地确定缓存区大小是非常必要的。因此,装配线中A车型底盘线工艺和B、C车型底盘线的工艺信息非常重要,其对应的工艺信息分别见表1、表2所列。

对于 A车型底盘线,每个工位的加工工序时长均为6.67 min,每个工位长度为7 m,而实际采用高架线运送方式,如果设置高架线的运送速度为1.05 m/min,刚好可以在规定的时间内完成相对应的加工任务,那么可以认为该设定是满足工艺需要的。

对于 B、C车型底盘线加工过程,每个工位的加工工序时长为3.75 min,每个工位长度为7 m,而实际采用板链线运送方式,如果设置板链线的运送速度为1.866 m/min,刚好可以在规定的时间完成对应的加工任务,那么可以认为该设定是满足工艺需要的。

表1 A车型底盘线工艺

表2 B、C车型底盘线工艺

2 装配线参数化建模

装配线参数化建模是提高建模效率最有效的方法之一,提高建模效率可以有效地加快生产计划的进行[5]。为了实现装配线工艺设计和三维装配流程一体化,构建装配线参数化物流模型,在Delmia/QUEST软件平台上,利用离散事件仿真工具(queuing event simulation tool,QUEST)软件[7]的批量控制语言(batch control language,BCL)和模拟控制语言 (simulation control language,SCL)对模型进行参数输入[6]。具体参数化建模实施过程如图2所示。

图2中,双向箭头表示数据之间相互索引和调用,并且展示了从工艺信息数据库到QUEST模型参数化设置的过程。通过Excel的建立,将装配线相关模型工艺信息录入到Excel已定义好的模型参数配置界面中,然后通过VBA(visual basic for applications)语言将相关工艺信息转换成QUEST可识别的BCL和SCL程序语句。该程序语句可以自动对模型进行参数化设置,Delmia/QUEST通过执行上述程序语句,快速自动生成三维仿真模型并对模型进行参数化设置。

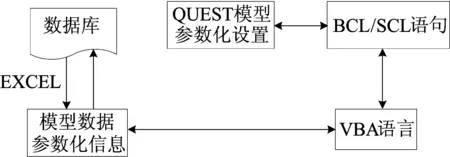
图2 物流参数化建模实施过程

3 仿真优化基本原理和模型建立

3.1 仿真优化基本原理

与其他一些简单产品的装配过程相比,汽车装配线具有自动化程度高、工艺路线复杂的特点,现有的装配线缓存区数量配置问题的相关理论比较少。在装配线设计初期阶段,需要将空间利用率、人员数量和工艺路线的布置情况考虑进去,而用传统的数学建模方法来求解关键位置缓存区大小的方法很难对装配线工艺约束、空间布局约束、路径约束等进行准确地建模[7]。文献[8]提出将传统优化算法和仿真模型结合起来,以此来解决装配线的关键位置缓存区优化问题。基于该方法,本文在Delmia/QUEST软件中建立仿真模型,然后将仿真和遗传算法结合起来,从而确定关键位置缓存区最优数量,实现装配线动态平衡和高空间利用率,提高工位利用率,降低生产成本。

3.2 仿真优化模型的建立

基于上述装配线的工艺信息,采用以遗传算法为核心的仿真优化算法。该问题的数学模型描述为:在给定的装配工艺信息、车间布局、物流路径等约束条件下,确定关键位置缓存区的最优大小,使得在装配线工位利用率满足一定的要求下,达到生产线平滑指数最小和产能最大。数学模型描述如下:

min SI=f(M1,M2,…,Mm,N1,N2,…,Nn),

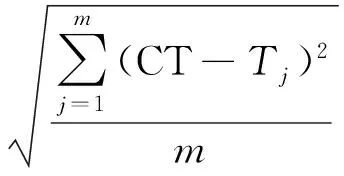
(1)

(2)

Kimin≤Ki≤Kimax

(3)

(4)

X(M1,M2，…，Mm,N1,N2，…，Nn)≤0

(5)

Y(M1,M2，…,Mm,N1,N2,…,Nn)≤0

(6)

Z(M1,M2,…,Mm,N1,N2,…,Nn)≤0

(7)

其中,SI为平滑指数,SI越小表示生产线工位的负荷越平衡;r1、r2分别为A车型底盘线和B、C车型底盘线的工艺权重,因为2种底盘线的工艺复杂程度不同,选取r1=0.6,r2=0.4;m为A车型底盘线的工位数;n为B、C车型底盘线的工位数;CT为生产节拍;Tj为第j个工位的加工时间;d为总产能;dp为对应车型的产能,用JPH(jobs per hour)来表示;Kimin和Kimax分别为第i个缓存区的最小数量和最大数量;ηj为第j个工位的工位利用率,并保证满足最低工位利用率ηjmin;X(*)、Y(*)、Z(*)分别为生产线各个工位必须满足的工艺约束、布局约束、路径约束。

(3)式表示在满足空间尺寸、装配工艺的条件下,可供选择的缓存区数量边界值;(4)式表示工位需要满足的利用率要求。

4 算法试验与结果分析

4.1 仿真优化算法的具体步骤

本文根据仿真优化的原理,采用基于遗传算法的装配线缓存区配置优化方法,实现装配线缓存区最优大小设置。初始方案下关键位置缓存区的数量见表3所列,初始方案下A、B、C 3种车型的产能均为5 JPH。

表3 初始方案关键位置缓存区数量配置

该仿真优化方法由主控流程、遗传算法和仿真模型3个部分组成。主控流程控制优化方法的全部流程包括初始种群如何生成、数据如何传递和种群信息如何显示问题;遗传算法主要用于缓存区配置方案的确定;仿真模型负责种群适应度的计算。在这3个组成部分的相互协调配合下,完成装配线缓存区数量的最优配置问题。与传统优化下的遗传算法相比较,仿真优化下的遗传算法具有如下特点[9]:① 目标函数值是通过仿真试验并对仿真结果分析得到的;② 仿真优化的效率瓶颈现象不是出现在传统算法中的算法迭代过程中,而是出现在仿真过程中。因此,在设计遗传算法时,上述问题都要仔细考虑。

(1) 编码设计与初始解生成。为了避免遗传算法过早收敛,拟采用随机数的方法生成初始种群。具体步骤如下:① 确定装配线缓存区大小的范围[Kimin,Kimax];② 在装配线缓存区对应基因位上产生一个[Kimin,Kimax]的随机数ri;③ 将对应缓存区的数目导入到仿真模型中,然后将该值赋给该个体的目标值基因位,同时将标志位值变为0;④ 重复以上步骤N次,可以产生一个包含N个个体的种群。

在装配线规划好的前提下,第i位基因位上的值,代表第i个缓存区的数量K。依据上述步骤随机生成初始解,然后依据初始解将装配线关键缓存区数量输入到Delmia/QUEST仿真模型中,进行仿真运行,得到目标函数SI和d的数值。一组初始解如图3所示。

(2) 选择与交叉操作。为了产生的新个体既能继承父代的优良性能基因,又能保持子代的基因多样性,采用经典的轮盘赌机制从父代选取个体生成下一代,利用两点交叉方式进行基因替换、重组生成新的个体。由于双亲都是可行解,交叉后产生的必然是可行解。交叉前后的2种可行解如图4所示。

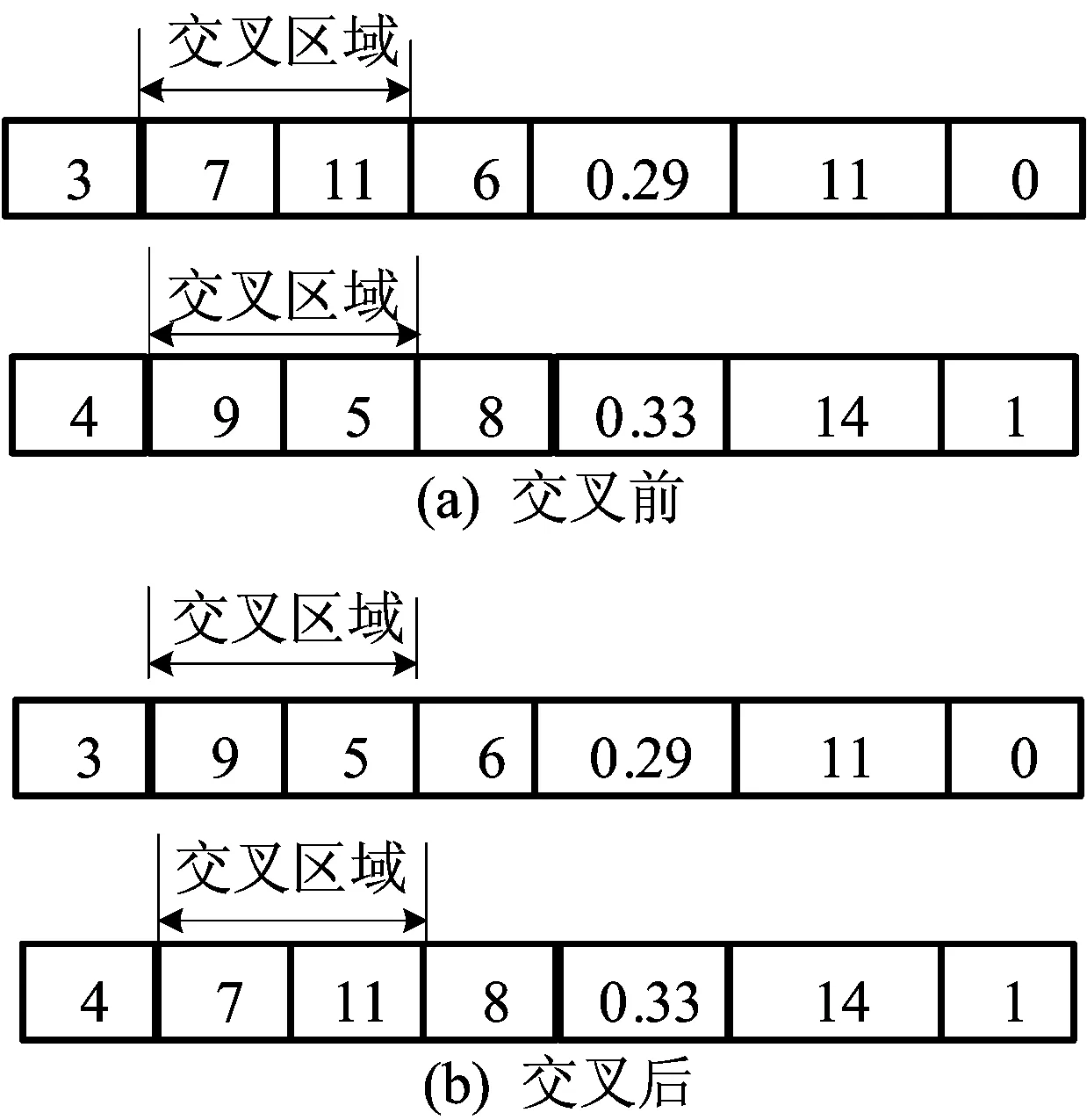
图4 选择与交叉运算

(3) 变异与迭代。变异的本质是一种随机算法,目的是维持群体的多样性,而变异算子的出现是遗传算法局部搜索能力优良的数学体现。为保证交换基因位后的染色体所定义装配单元的属性不变,采用均匀变异。在每个缓存区定义的数量[Kimin,Kimax]之间,产生一个随机数,如图5所示。将对应缓存区的数量值输入仿真模型,进行遗传算法的迭代过程。观察目标值的大小变化,如果出现目标值连续25次没有变化,那么停止迭代过程。

4.2 仿真优化结果

采用Matlab的遗传算法求解,该算法包含与遗传算法相关的函数[10]。经过迭代、计算得出,遗传算法在第83代收敛,目标值为0.23。优化后关键位置缓存区的数量配置见表4所列,优化后A、B、C 3种车型的产能分别为7、6、6 JPH。

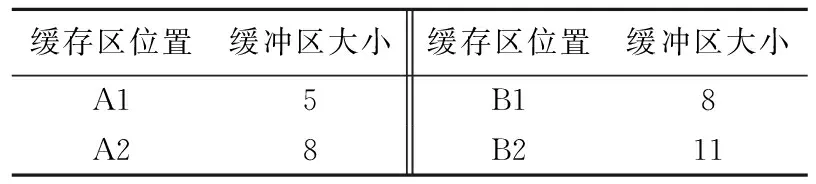
表4 优化后关键位置缓存区数量配置

表4配置方案下,在Delmia/QUEST中建立物流模型,通过仿真分析获得各工位类型的利用率,并与初始方案下各工位利用率进行对比,结果如图6所示。

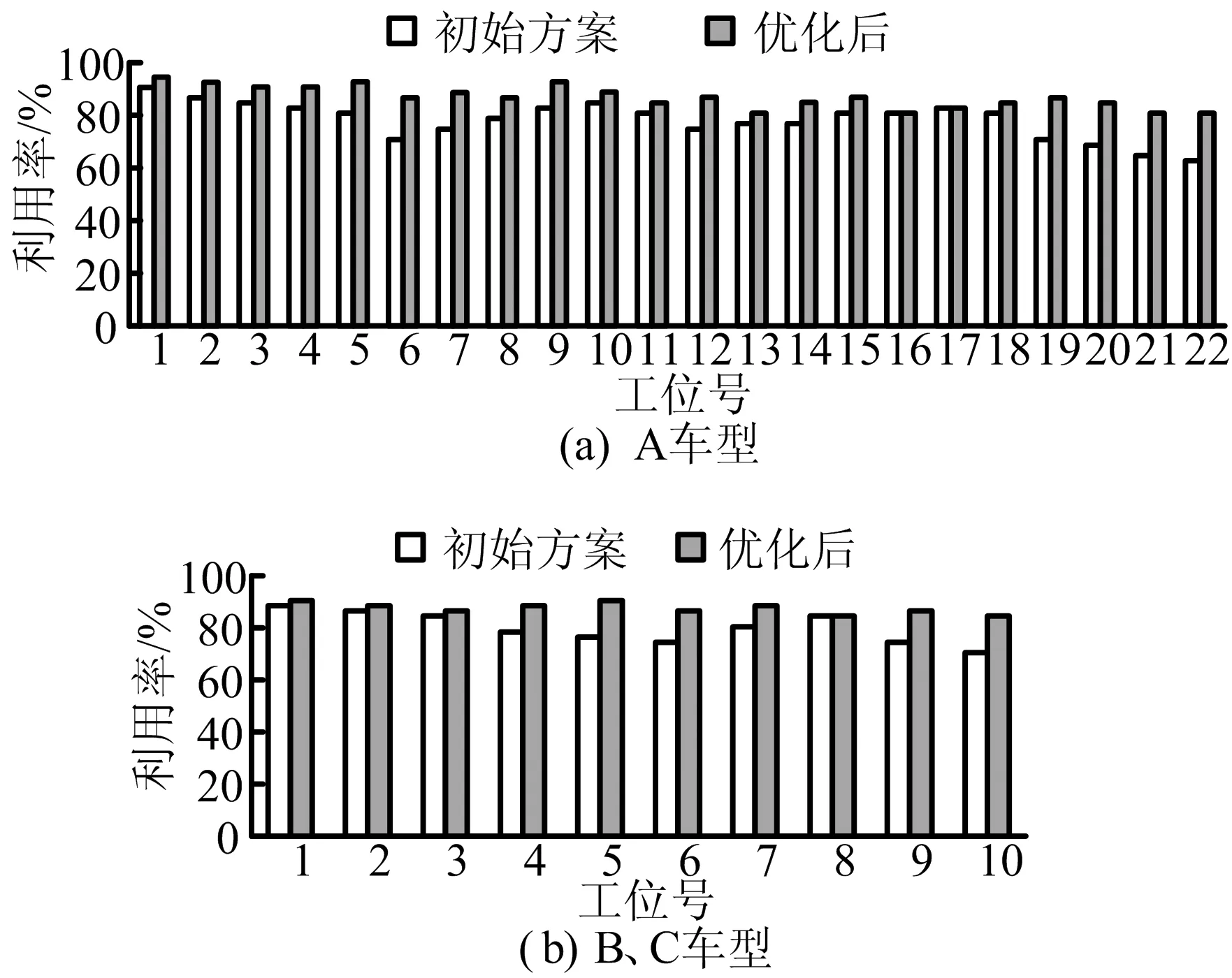
图6 3种车型底盘线工位利用率

图6中，各装配单元间的负荷基本平衡,与初始方案相比具有很大的改善。

5 结 论

本文研究表明,通过以遗传算法为核心的仿真优化算法可以对汽车装配线关键位置缓存区数量进行优化;基于Delmia/QUEST的装配线仿真对于装配线动态平衡和工位利用率起到了辅助验证的作用。

遗传算法和计算机仿真相结合可以在装配线工艺规划优化中起到优化和验证的效果,从而解决了装配线关键位置缓存区数量优化问题,实现了装配线动态平衡,达到了提高工位利用率和减少生产成本的目的。

[1] 周济.智能制造——“中国制造2025”的主攻方向[J].中国机械工程,2015(17):2273-2284.

[2] 孙连胜,宁汝新,王新永.虚拟制造中生产线可视化设计[J].北京理工大学学报,2002,22(1):32-35.

[3] 曹国安,王丽,万文杰,等.离散型制造企业车间生产物流系统的优化[J].合肥工业大学学报(自然科学版),2011,34(5):665-670.

[4] 齐继阳,竺长安.基于DELMIA-QUEST制造系统仿真模型的研究[J].机械设计与制造,2010(4):113-115.

[5] 王伟,张鹏,吴波,等.装配车间生产系统的物流仿真分析[J].机械设计与制造,2013(12):259-261.

[6] 于海斌,朱云龙.可集成的制造执行系统[J].计算机集成制造系统,2000(6):1-6.

[7] 张远春.多品种混合装配车间关键资源建模与优化[D].上海:上海交通大学,2011.

[8] 王国新,宁汝新,王爱民,等.仿真优化在制造系统中的应用现状及发展趋势[J].系统仿真学报,2008,20(1):1-6.

[9] 孙中悦.车辆路径问题的仿真优化方法研究[D].北京:北京交通大学,2011.

[10] 扈静,蒋增强,葛茂根,等.基于改进遗传算法的混合装配生产线平衡问题研究[J].合肥工业大学学报(自然科学版),2010，33(7):1006-1009,1019.

Optimizationofbufferareaconfigurationofmixed-modelautomobileassemblylines

HUANG Peng1, TANG Huohong1, HE Qichang2, WANG Ke1

(1.School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China; 2.School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The processes of the mixed-model automobile assembly lines are complex and the number of buffer area of the key position is difficult to determine, which makes the assembly lines process inefficient. This paper aims at optimizing the smoothness index and maximizing the product ability, which are essential factors in evaluating the assembly lines. The simulation model is established through setting the process information, spatial layout and logistics route as restrict conditions and the number of buffer area of the key position as variables. In view of the complexity of this problem, a simulation optimization algorithm based on genetic algorithm is put forward, and the optimization in the Delmia/QUEST simulation environment is conducted to get the optimal number of buffer area of the key position and to realize the dynamic balance and the maximum product ability of the assembly lines.

mixed-model assembly line; number of buffer area; genetic algorithm; simulation optimization; dynamic balance; maximum product ability

2016-02-25；

2016-03-29

上海市科委资助项目(15111107502)

黄 鹏(1991-),男,湖北襄阳人,合肥工业大学硕士生;

唐火红(1973-),男,安徽池州人,博士,合肥工业大学副教授,通讯作者,E-mail:tanghh@ustc.edu.cn.

10.3969/j.issn.1003-5060.2017.09.004

TH164

A

1003-5060(2017)09-1168-05

(责任编辑 胡亚敏)