基于非凸函数的矩阵秩最小化理论
(山东科技大学 山东 青岛 266590)
基于非凸函数的矩阵秩最小化理论
王淑琴
(山东科技大学山东青岛266590)
近来,在计算机视觉、数据挖掘等领域人们越来越热衷于利用秩最小化方法优化模型。由于在求解秩函数的过程是一个NP难的非凸优化问题,本文选取对数行列式函数作为秩函数的非凸近似,采取增广拉格朗日乘子法(ALMM)求解对数行列式线性最小二乘模型。通过数值实验验证本文提出的算法较现有的求解核范数矩阵秩最小化问题的算法更高效。
矩阵秩最小化;对数行列式函数;增广拉格朗日乘子法
一、引言
矩阵的秩最小化问题是为了寻找一个满足给定约束条件的低秩矩阵X∈Rn×m,即:
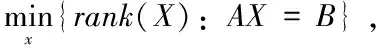
(1)
这里,X是数据矩阵,A∈Rp×n,B∈Rp×m。这是一个NP难的非凸优化问题,学者们通常采用矩阵的核范数作为矩阵秩函数的凸近似来求解此类问题,即:
(2)
这里,||·||*为矩阵核范数,即矩阵的所有非零奇异值之和。然而,当矩阵的奇异值非常大时,用矩阵的核范数近似秩函数效果一般,彭冲等在文献[1]中求解子空间聚类问题时发现,利用对数行列式函数对矩阵秩函数进行近似的效果较好,优于核范数近似效果。基于此,本文中我们考虑用对数行列式函数
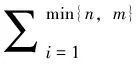
(3)
近似矩阵的秩函数。这里的σi是X的奇异值,其中i=1,…,min{n,m}。
在实际应用中,数据矩阵B可能会被噪声污染,引入最小二乘的思想[1,2],建立如下的对数行列式函数正则化最小二乘模型:
(4)
这里,μ>0,||·||F表示矩阵的F范数。
二、增广拉格朗日乘子法
引入一个辅助变量Y∈Rn×m,模型(5)可以被等价表示为:
s.t.X=Y
增广拉格朗日函数为:
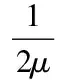
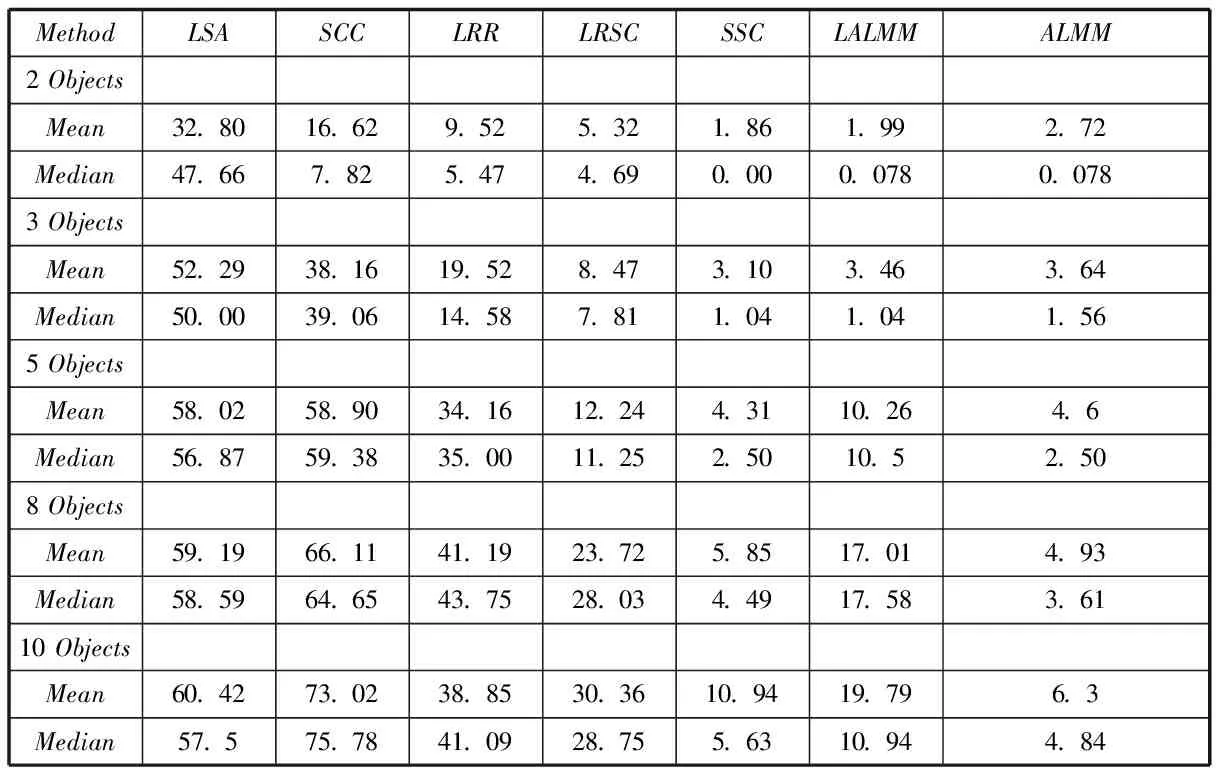
其中θ∈Rn×m是拉格朗日乘子,β>0是惩罚参数。当n Yk+1=(I-AT(AAT+βμI)-1A)(ATB+βμXk-μθk) 因为LALMM的收敛性在前面已经分析过,这里我们只导出KKT条件 省略了ALMM的收敛性分析。 结合(7)式,ALMM算法被概括如下: 算法1ALMM输入:A,B,μ>0,β>0,迭代的最大数量Kmax. 1:初始化:SetX0∈Rn×m,θ0∈RN×m,K=0.2:循环:a.Yk+1=(ATA+βμI)-1(ATB+βμXk-μθk)b.Dk+1=Yk+1-1βθk.c.利用命题1解Xk+1d.θk+1=θk-β直到Untilk>kmax或者{Xk,Yk,θk}收敛 输出:X∗=Xk. 在本节中,我们采用Extended Yale B①[13]数据应用到人脸识别,将2、3章中提出的算法与LSA[5],SCC6,LRR,LRSC[6],SSC的有效性进行对比。本文所有的实验都是在Windows 8系统MATLABR2013a中运行的。 表1 聚类误差百分比 【注释】 ①http://vision.ucsd.edu/?leekc/ExtYaleDatabase/ExtYaleB.html [1]M.Fazel,H.Hindi,P.B.Boyd.Log-det heuristic for matrix rank minimization with applications to Hankel and Euclidean distance matrices[C].American Control Conference,2003.Proceedings of the 2003.IEEE,3,2003,2156-2162 [2]C.J.Hsieh,P.A.Olsen.Nuclear norm minimization via active subspace selection[C].Proceedings of the 31st International Conference on Machine Learning(ICML-14).2014:575-583 [3]J.F.Sturm.Using SeDuMi 1.02,a MATLAB toolbox for optimization over symmetric cones[J].Optimization methods and software,11(1-4),1999,625-653 [4]R.Glowinski,P.Le Tallec.Augmented Lagrangian and Operator Splitting Methods in Nonlinear Mechanics[M].SIAM Studies in Applied Mathematics,Philadelphia.1989 王淑琴(1992-),女,山东滨州,硕士研究生,山东科技大学,研究方向图像处理。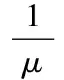

三、实验结果及分析