超颖表面原理与研究进展

李天佑，黄玲玲，王涌天

(北京理工大学 光电学院，北京 100081)

超颖表面原理与研究进展

李天佑，黄玲玲*，王涌天

(北京理工大学 光电学院，北京 100081)

超颖表面是一种特殊的二维亚波长阵列结构，具有很强的光场调控能力，兼有超薄、低损耗、易加工等优势，表现出广阔应用前景，近些年吸引了广泛的研究兴趣。本文将综述超颖表面的原理与研究进展，简要分析已报道的超颖表面类型，并重点介绍其在广义折反射、偏振转换、光束轨道角动量操控以及计算全息中的应用。超颖表面设计灵活、功能强大，有望在诸多应用中取代传统光电器件。未来基于超颖表面的新型、宽带、高效率、多功能以及主动可调功能器件等将是其重要的发展方向。

超颖表面；偏振转换；光束轨道角动量；计算全息

1 引 言

光学元器件和设备通过以指定方式调控光的振幅、相位以及偏振，从而得以实现对光束传播方向与波前的操纵，并在显示、传感与通信等应用中赋予所需的信息。传统的光学器件往往通过光在特定介质中累积传播的光程来达到对光的调控[1-2]，具有较大的体积，难以适用于未来集成化、微型化器件发展趋势。

超颖材料(Metamaterial)是一种由亚波长周期微纳结构构成，具有自然界材料所不具备的超常物理特性的人造电磁材料[3]。因其独特的特性，超颖材料在过去的二十年间引起了广泛的研究[4-12]，并在超分辨成像[13-14]，光学隐形[15-16]等领域有着潜在的应用前景。传统的超颖材料可视为等效介质(亦称为体超颖材料，Bulk Metamaterial)，对光场的调控仍依赖于光在材料中的传播以及相互作用的积累。超颖材料通常使用金属材料并利用了结构的谐振响应，具有难以避免的高损耗与色散特性；同时亚波长三维结构不易加工制造，这些因素限制了超颖材料的进一步研究与应用。

为了克服超颖材料的诸多缺点，人们想到了“降维”的办法，将研究重点转向平面二维结构。超颖表面(Metasurface)是一种二维平面超颖材料，通常由亚波长尺寸的周期，准周期或者随机的单元构成，其厚度远小于波长，可视为二维表面[17-18]。超颖表面利用每个单元结构对入射光场的强烈响应来改变局部光场的振幅和相位，从而以亚波长尺度对光场振幅与相位进行调制，进而实现对近场与远场的调控。这种远小于入射波长的厚度使得超颖表面不再依赖光在介质中传播的光程累积，因此介电常数、磁导率、折射率等参数不再被用来描述超颖表面，而往往是用表面阻抗、振幅、相位、偏振等参量来描述其物理性质。超颖表面在具有很强的光场调控能力的同时，兼有超薄、低损耗、易加工等优势，在奇异光学[19]、光束整形、偏振调控[20]、光学全息技术[21]、光束轨道角动量操控[19]等方面具有广阔的应用前景。

超颖表面本质上是一种有着不同几何结构以及亚波长空间间隔的光学天线阵列，通过设计每个纳米天线辐射场的相位延迟，利用惠更斯原理，能够实现对出射波前的任意调控。这与微波波段的频率选择表面(Frequency-Selective Surface，FSS)有着本质的不同，频率选择表面没有空间可变的电磁响应。相比传统光学元件以及体超颖表面，超颖表面具有一些显著优点[22]：(1)超薄化。超颖表面能够在远小于入射波长的尺度上实现对入射光场振幅、偏振与相位的调控，显著减小了光在介质中传播的损耗。(2)亚波长像素。超颖表面能够以亚波长尺度的像素对光场进行调控，能有效避免在传统衍射光学元件中多级衍射的串扰，在微型集成光电系统中有着广阔的应用前景。(3)宽带特性。通过特定的设计，超颖表面能够在宽波段对光场进行同样的调制，具有弱色散或者无色散的特性。上述优点再加上超颖表面在设计灵活性以及低成本制造方面的优势使得其有望成为新一代超薄、小型光场调控器件。

本文将从以下两方面对超颖表面的研究进展进行了概述，并结合作者对超颖表面的认识对超颖表面的发展提出了展望。

(1)超颖表面的基本分类。按照光场透反射空间、阵列结构类型以及相位调控机理，超颖表面可分为不同大类。

(2)超颖表面的功能应用研究现状，包括利用超颖表面的异常折射/反射现象、基于超颖表面的任意波前调控以及基于超颖表面的偏振转换器件研究。

2 超颖表面调控机理研究现状

2.1基于光学天线的谐振响应

光学天线[22]通常具有多种多样的结构，包括金属/介质颗粒，金属薄膜上的小孔以及上述二者的多层叠加。光学天线能够利用其局域表面等离激元谐振响应调控天线辐射场的相位，从而在亚波长尺度实现对光场的操控。设计特定结构的光学天线是此类超颖表面的核心思想。

2011年，哈佛大学的Yu等人[19]首次使用V型天线实现了对表面相位的不连续调控。V型天线由两个长度均为h的臂构成，他们之间的夹角为Δ，如图1(a)所示。V型天线具有所谓的双频谐振特性，即该天线可以支持“对称”和“反对称”模式。对称模式近似成长度为h的单臂天线的情形，因此其谐振波长发生在h≈λeff/2处，其中λeff为等效波长；反对称模式近似为长度为2h的直臂天线，其谐振波长发生在2h≈λeff/2处。在两个谐振波长附近，天线对相位的改变非常显著。两种谐振模式能够被入射光独立激发，并且一般会导致散射场与入射场具有不同的偏振态。通过设计天线的结构参数，可以使得在线偏振光入射时，其正交偏振态的出射光拥有对相位和振幅的调控能力，相位的调制范围可以涵盖0到2π，散射场的振幅则由天线的结构确定。

图1 (a)V型天线结构示意图；(b)Y型天线结构示意图[22] Fig.1 (a)Schematic of the V-shaped antenna. (b)Schematic of the Y-shaped antenna[22]

V型天线的一种变型是Y型天线[25]，如图1(b)所示。V型天线臂长和夹角的改变会使得“对称模式”和“反对称模式”对应的谐振频率产生漂移，为了改变这一特性，可以加入另一臂L作为一个新的调控自由度。当改变L的长度时，可以保证沿Y型天线对称轴方向的偏振光谐振频率不变，而垂直于对称轴方向的谐振频率可以独立调节。当Y型天线具有C3对称性时，即天线各臂长相等且各臂之间夹角为120°时，不存在偏振转换特性。在线偏振光的激发下，V型天线与Y型天线的散射场一般来说是椭圆偏振光，当选择合适的入射偏振态与出射偏振态的正交组合，可以实现出射光相位在0到2π范围内的精确控制。这类基于光学天线的相位调制机制依赖天线的谐振响应，因此本质上具有窄带的特性，并由于振幅与相位并不能独立调制，需要仔细设计结构的参数。

2.2惠更斯表面

为了提高透射光的效率，Pfeiffer等人[26]提出了一种有别于天线谐振方法的表面结构。这种结构可以通过控制表面电、磁极化率(αe与αm)来达到完全消除反射的目的。表面等效电流与磁流正比于表面电极化率与磁极化率。通过调控表面极化率，并结合边界条件，散射波前能够获得任意形式。当某一表面满足

式中，η0为自由空间阻抗，则其复振幅透射系数可以表示成[26]:

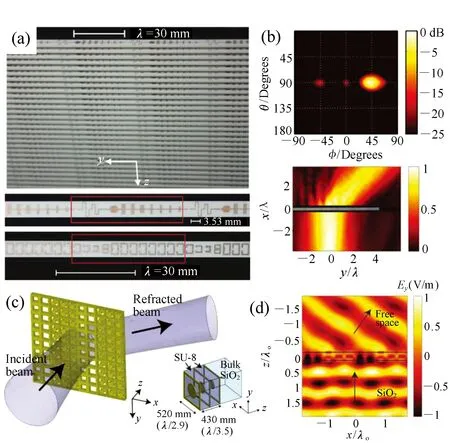
图2 (a)惠更斯表面样品实物图；(b)上半部分：实验测得的辐射图案；下半部分：测得的x-y平面磁场强度分布[26]。(c)光波段各向同性惠更斯超颖表面示意图与单元结构示意图；(d)在1.5 μm波长光照射下的异常折射光的仿真电场分布[27] Fig.2 (a)Photograph of the fabricated metasurfaces with anomalous refraction. (b)Upper panel: the measured radiative pattern; bottom panel: the distribution of measured magnetic field in x-y plane[26]. (c)Schematic of an optically thin isotropic Huygens′ metasurface and its unit cell. (d)Simulated electric field distribution of the anomalous beam at 1.5 μm[27]

式中，ω为入射光频率。当αe主要为实数时，则透射率接近1，并且透射相位可以涵盖0到2π的范围。Pfeiffer等人在微波领域进行了了原理验证[26]，如图2(a)、2(b)所示。图2(a)为样品实物图，图中底部为样品单元结构，基底顶侧的微型铜线路可提供所需的电极化电流，底侧的开口谐振环可以提供必要的磁极化电流。图2(b)为所得实验结果，在达到光线偏折效果的同时获得了高达86%的透过率。惠更斯表面的设计原理在其他频段同样适用，光学领域的表面结构如图2(c)所示[27]。Pfeiffer等人设计了一种各向同性结构，在1.5 μm波长处实现了对入射光的调制。这种各向同性结构能够有效降低样品加工方面的困难。可独立对振幅与相位进行调控的，利用全介质结构以及应用于全息领域的惠更斯超颖表面也于近期被报道[28-31]。

2.3基于贝里相位(Pancharatnam-Berry Phase)的超颖表面

上述两种机理本质上都是色散的，其相位、振幅调制特性在入射光频率发生变化时往往不再适用。而基于贝里相位的超颖表面具有宽频带的特性，通过相同单元结构的不同空间朝向即可实现连续的相位调制，本质上是一种无色散的调制机理。

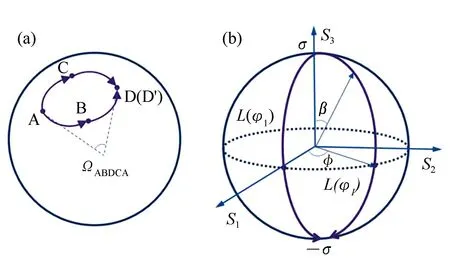
图3 贝里相位与偏振演化路径。(a)初态沿不同路径演化到同一终态所对应立体角；(b)当圆偏振入射，经过纳米棒天线阵列，并取相反圆偏振时，光的偏振态演化路径。偏振态演化路径分别经历σ→φ1→σ与σ→φ2→σ[22]，其中φ1和φ2分别为两不同天线的方位角 Fig.3 Pancharatnam-Berry phase and the evolution of polarization. (a) Different polarization evolution path in Poincaré sphere. (b)The polarization evolution path for metasurfaces composed of nanorods array when illuminated with circularly polarized light and selected orthogonal handedness circularly polarized light. The polarization state undergo σ→φ1→σ and σ→φ2→σ respectively, where φ1 and φ2 are the azimuthal angle for two different nanorods, respectively

贝里相位也称为几何相位，1956年，Pancharatnam在研究中指出，当一束偏振光在其偏振态经过多次改变后，其初末偏振态之间的相位改变与其偏振态改变过程在邦加球表面划过的轨迹有关[32]，1984年，Berry[33]重新研究了这一现象，并指出其具有几何性质的一面。如图3(a)所示，考虑邦加球上某一初始偏振态A在沿两个不同路径变化到达同一最终态D和D′。D和D′虽然偏振态相同，但二者相差一个相位差，即贝里相位，可由下式表示：

式中，ΩABCDA为邦加球面上两条演化路径所围立体角。当某一手性为σ的圆偏振光入射，经天线散射作用后终态变为相反手性的圆偏振光σ。若中途经过两个空间电极化方向分为φ1和φ2的纳米天线，比如纳米棒，其空间朝向就是其空间电极化方向，它们产生与本身电极化方向一致的线偏振态，偏振方向分别为φ1和φ2，分别对应邦加球赤道上两个点。经过两段不同的演化路径之后，根据贝里相位原理，最终相同的终态之间存在 2(φ2-φ1)的相位差，如图3(b)所示。偏振变化与相位差的关系亦可以由琼斯矩阵清楚得到[34-35]。一般来说，一个各向异性散射体的琼斯矩阵可以表示为:

其中

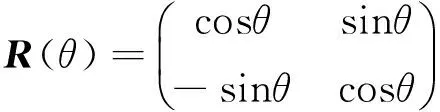
为旋转角为θ的旋转矩阵，t1和t2分别为入射光沿着该各向异性散射体主轴方向的前向散射系数。若给定右旋圆偏振光入射，通过这一各向异性散射体后电矢量可以表示为[36]

等号右边第一项表示与入射圆偏振光旋向相同的散射光,第二项表示拥有与入射旋向相反的散射光，但是附带了2θ的贝里相位。Kang等人[36]利用这一原理，设计了一种U型小孔相位梯度超颖表面。通过仔细设计U型孔的结构以及旋转U型孔的朝向，可以使得t1与t2振幅相同但是相位差正好为π，于是入射圆偏振光可完全转化为反旋向的圆偏振光并携带所需相位，并实现光束偏折与汇聚等作用，如图4中(a)、(b)所示。改变入射光的旋向可以改变光线偏折方向以及将光线由汇聚变为扩散效果。Huang等人利用贝里相位原理，采用棒型纳米天线实现广义折反射现象[37]、宽带涡旋光生成(图4(c))、以及三维纳米全息[21]等应用。利用该原理的彩色全息方法也得到了证实[38]。

图4 基于贝里相位的几类超颖表面及其应用。(a)手性可调异常透射；(b)手性选择性双极性透镜[36]；(c)手性选择性宽带涡旋光束发生器[37] Fig.4 Several metasurfaces and their applications based on Berry phase. (a)Helicity-dependent tunable anomalous transmission. (b)Helicity-dependent dual-polarity metalens[36]. (c)Helicity-dependent broadband vortex beam generator[37]

值得注意的是，贝里相位其本质机理是无色散的，不会因为入射光频率变化引入相位失真，但是对于特定结构总是存在一定的操作带宽。一方面，入射波长须数倍于超颖表面结构尺寸以保证亚波长的要求；另一方面，入射波长不能太大以保证天线的散射效率。其结构的散射效率仍取决于局域表面等离激元谐振(Localized Surface Plasmon Resonance)。

2.4其它设计方法

其中，E和B，Ec和Bc分别为两互补屏的后向散射场。灵活运用互补结构可以增大超颖表面的设计灵活性[40-41]。

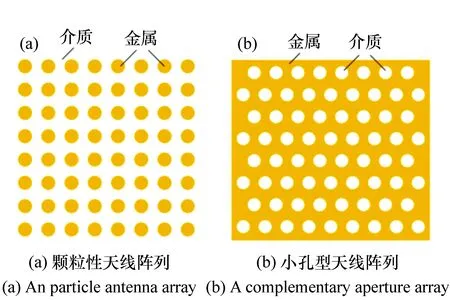
图5 两类结构互补的超颖表面：(a)颗粒性天线阵列；(b)小孔型天线阵列[22] Fig.5 Two types of complementary metasurfaces.(a)An particle antenna array. (b)A complementary aperture array

超颖表面设计亦可以使用反射阵列，反射阵列由金属天线，薄介质层以及金属基底构成。这类反射阵列受到早先有关微波与厘米波研究的启发[42]，该方法利用了天线与其镜像天线的耦合，从而达到更广的相位响应范围。

相当多的研究关注亚波长金属结构，但是金属在光频段的欧姆损耗限制了超颖表面性能的提高。而低损耗，高折射率介质构成的超颖表面受到了越来越多的关注。根据米氏散射理论，介质可在光波段发生强烈的电磁散射，散射后的电磁场可以写为电磁多级子散射场的级数和的形式[43]。与金属结构主要由电子谐振影响结构性质不同，在几何结构规则的介质谐振子中，最低阶的谐振模式是磁偶极谐振，二阶模式是电偶极谐振[44-46]。更高阶的模式对总散射场贡献很小，一般可以被忽略[47]。

利用介质作为超颖材料的结构单元也曾吸引了相当多的研究兴趣，并在不同波段实现了负的电磁响应[48-50]。一般来说，电、磁谐振分别处于不同的频率时，介质谐振子只能提供最多 π的相位变化[2]；为了使相位变化涵盖2π的范围，可以改变介质单元的结构[51]或者是结构之间的间距[52]，使得电、磁偶极子谐振重合，实现完全的相位调控。一系列结构诸如块状[53]、圆柱形[52,54]、椭圆柱形[55]等纳米结构均可以实现对相位的完全调控甚至同时对偏振与相位完全调控[55]。而基于贝里相位的原理，也可利用介质材料实现对光场相位的完全调控，例如采用具有连续方位角变化的介质条结构[56]。

3 超颖表面功能应用研究现状

3.1基于超颖表面的广义折射和反射效应

光在经过两种均匀材料截面时，根据斯涅耳定律以及菲涅尔公式可以确定光的反射角、透射角、反射系数以及透射系数。若光经过界面时，在亚波长尺度内产生了显著的相位突变，则光线在经过该界面时便不再遵守传统的斯涅耳定律，而新的传播规律仍然可以由费马原理(Fermat′s Principle)推导而得[19]。

式中，λ0是真空中的波长，dΦ/dx是平面上的相位梯度。如果dΦ/dx=0，则广义折射与反射定律退化为传统折射与反射定律，当dΦ/dx≠0时，偏离传统定律的折射光与反射光称为异常折射光与异常反射光。

对于更一般的情况，即入射波矢与反射、折射波矢不处于同一平面时，费马原理同样适用，由此可以得到更一般的广义折射与反射定律[57]：

公式中的角度详见图6，式(8)与(9)分别代表平行或垂直于入射面的相位梯度。

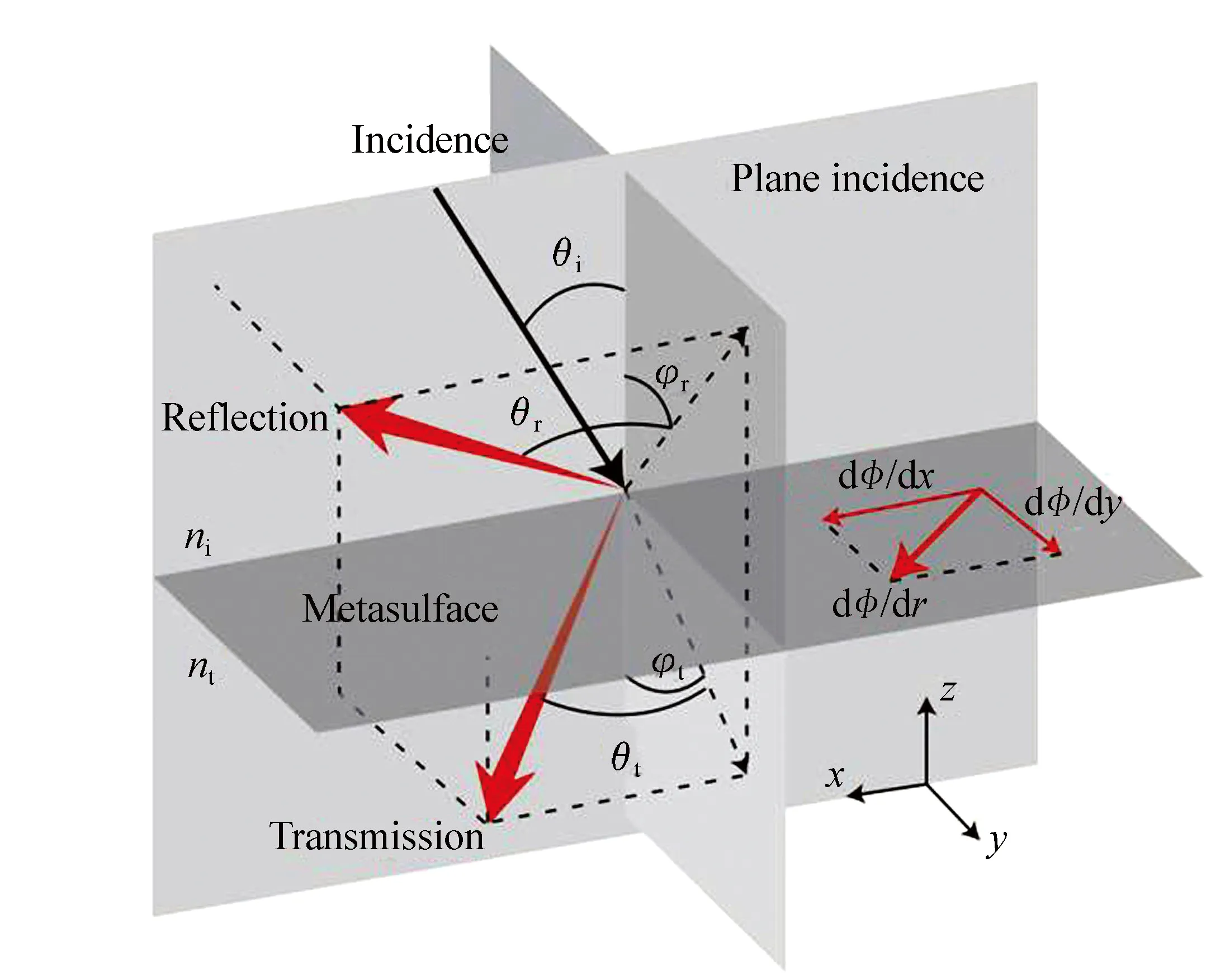
图6 一般情况的广义折射、反射示意图，沿界面表面的相位梯度为dφ/dr[1,57] Fig.6 Schematic of generalized anomalous refraction and reflection; the interfacial phase gradient is dφ/dr[1,57]

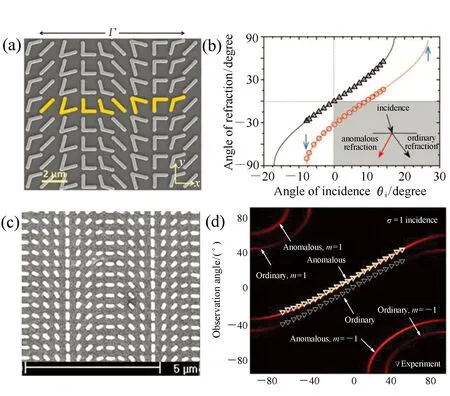
图7 (a)V型天线阵列SEM样品图像；(b)实验测量的异常折射数据。(c)纳米棒阵列SEM样品图像；(d)入射手性σ=1时正常反射现象与异常反射现象 Fig.7 (a)SEM image of array of V-shaped antennas. (b)Measured data of anomalous refraction. (c)SEM image of array of nanorods. (d)Ordinary and anomalous reflection with incident helicity σ=1

Yu等人[19]最早验证了这种广义折反射现象，如图7(a)、7(b)所示，通过仔细选择V型天线的结构，保证线偏振光垂直入射下各个V型天线沿其正交偏振方向的散射光振幅近似相等且相邻单元散射光之间拥有恒定的相位差，从而保证恒定的相位梯度，则可以实现线偏振垂直入射下相应正交偏振折射光线任意偏折。Huang等人采用纳米棒阵列验证了依赖手性的广义折射与反射定律，如图7(c)、7(d)所示，即利用贝里相位原理控制相邻单位之间的相位差，并提出了广义光栅方程[37]，即当相邻纳米棒的间隔与波长相近时，该周期结构会产生高衍射级次，各衍射级次传播方向满足：

ntsin(θm)-nisin(θi)=

式中,m代表衍射级次，σ代表入射圆偏振光的手性，可取±1。当m≠0时，存在异常衍射光。

这种广义反射与折射现象同样可以应用于其它波段。Zhang等人[58]利用一种C型天线，在太赫兹波段实现了宽频段的波束偏折。多种利用反射阵列结构实现广义反射现象也得到证实[59-60]：Sun等人实现了H型反射天线[59]与块状反射天线[60]的广义反射，理想情况下，所有入射能量都会转化为异常反射能量，利用块状反射天线可测得反射阵列超颖表面效率达80%，远大于效率仅为10%～20%的透射性V型天线。

3.2基于超颖表面的任意相位梯度调制

3.2.1 基于超颖表面的平板透镜

透镜是光学系统中的重要元件，具有成像，照明，聚焦等功能[43]。传统透镜需要利用光波在透镜材料中传播的相位积累来达到控制波前的目的，因此需要设计透镜的表面曲率以及采用合适的厚度，故传统透镜一般比较大。使用衍射光学元件[61]和梯度折射率结构[62]可以为透镜设计带来新的思路，可实现平板透镜，但由于自然界可用折射率材料有限，以及面临加工方面的困难，这种类型的平板透镜仍受到集成化、超薄化的挑战。

为实现平板透镜，超颖表面需要施加一个相位轮廓

用于将入射平面波转化为汇聚在焦距f处的球面波。显然若超颖表面相位满足上述分布，可以在实现高数值孔径的同时不会带来球面像差。Aieta等人[63]利用V型天线实现了1.55 μm波长处的平板透镜，如图8(a)所示。但这种平板透镜的效率相当低，仅有1%左右的入射光被汇聚。这是因为实验中仅采用了单层结构，且样品填充率比较低，并只采集了正交偏振光。为提高操作波长带宽以及转换效率，可以考虑使用反射型超颖平板透镜[64]，如图8(b)。同样，出于抑制背景光的目的，可以通过巴比涅原理[65]设计V型小孔天线阵列汇聚入射光。Sergei等人[66]通过计算全息图的原理，设计了一种反射式汇聚超颖表面，该超颖表面相位分布与计算全息图所得相位一致，从而可以获得单点以及多点聚焦的功能。

图8 (a)V型天线阵列构成的平板透镜[63]；(b)反射型超颖表面平板透镜结构单元及其仿真所得焦平面处的电场强度分布[64] Fig.8 (a)Flat lens consisting of an array of V-shaped antennas[63]. (b) The unit cell of flat lens made of reflect-array and the calculated electric field distribution on the focus plane[64]

基于贝里相位，可以利用纳米棒[67]或者U型小孔[36]设计平板透镜，这种平板透镜一般可以根据入射光的手性变更汇聚或者分散的功能。同样可以设计反射阵列[68]以达到增大转换效率的目的。

通过介质超颖表面也能够实现高效率平板透镜。通过采用高对比透射阵列(High-contrast Transmit Arrays,HCTAs)，利用单晶硅圆柱的半径变化实现对透射相位的调制，仅仅采用单层结构便实现了85%的透射效率以及72%的聚焦效率[54]。通过将圆柱换为椭圆结构可以获得更多的调控自由度，可以实现x、y入射偏振光分别汇聚到不同侧的效果[55]。最近，Mohammadreza等人[69]报道了一种工作在可见光波段，成像质量可匹敌目前最先进商业物镜的平板透镜。该平板透镜基本原理基于贝里相位，通过设计鳍状TiO2柱的参数使其达到半波片的作用从而最大化转换效率。精妙的加工工艺进一步完善了该平板透镜的性能。该方法制得的透镜最高获得了86%的聚焦效率并可分辨亚波长间距的纳米尺度特征，放大率可达170倍[69]。

一般来说上述平板透镜虽然没有球面像差，但是单色像差(Monochromatic Aberration)总是存在。当入射光不再垂直于平板透镜表面时，由于非垂直入射会引入一个附加的线性相位分布，透射光或者是反射光波前便不再是球面。此外平板透镜通常也具有色差(Chromatic Aberration)，通过设计耦合方型谐振子阵列(Rectangular Dielectric Resonators，RDRs)，可以使超颖表面拥有一个依赖于波长的相位分布来补偿这种色散累积的相位差，从而实现在1.3、1.5以及1.8 μm三个波长均能汇聚至同一焦点[70]，但是在其他波长处仍然存在着色差。宽波带消色差平板透镜的实现仍然具有一定的挑战性。

3.2.2 基于超颖表面的计算全息

全息图记录的不是一幅图像，而是看似杂乱的一系列振幅与相位信息，利用参考光照射全息图即可重构出虚拟的三维图像[71]。计算全息[72-74](Computer Generated Hologram， CGH)技术可以方便的获得重构目标物体所需的相位分布，超颖表面则可提供一系列对局部振幅、相位以及偏振的调控方法，因此是实现亚波长像素计算全息的一种有效工具。

Walther等人[75]提出一种金属孔径阵列，通过调节孔径的大小能够调控局部单元的振幅，从而实现远场全息图像。利用孔径的色散，同一样品在905 nm以及1 385 nm处可以获得两个完全不同的全息图，如图9(a)所示。Ni等人[76]设计一系列V型小孔，如图9(b)，使其可获得8级相位分布以及2级振幅分布。通过使用这小孔阵列在超颖表面近似地引入所需的振幅和相位，能够在远场获得所需的图像。

基于贝里相位的全息也被广泛研究。由棒型纳米天线的相位调控特性可知[37]，通过简单旋转纳米天线的朝向，即可记录三维物体计算全息图所需的相位信息，其方位角编码了连续可调的局域相位信息。对某一手性入射光，取相反手性的出射圆偏振光即可获得所需光学再现像[21]，如图9(c)所示。实验上可观察到实心三维飞机模型和一系列空心螺旋点阵。这种方法可以有效增大三维全息的视场角，实现零级光束同轴再现，并可以避免多级衍射像。单层透射型纳米棒阵列的成像效率往往不够高，适当优化单元结构并且采用反射阵列，可以获得更高的转换效率。Zheng等人[77]设计了一种反射阵列(图9(d))，使得沿纳米棒长轴与沿纳米棒短轴方向的线偏振光反射系数相位差在600～1 000 nm的范围内为π，从而该结构能起到半波片的作用，对于反射阵列可使得反射光完全转化为同旋向圆偏振光(反射阵列同旋向圆偏振光携带贝里相位信息)，极大地提高效率。同时Zheng等人采用了16级相位分布。实验证实了这一结构在825 nm波长处效率可达85%，并且在630～1 050 nm波长范围内拥有相当高的成像质量。

图9 基于超颖表面的全息。(a)金属小孔阵列，以及入射波长分别为λ1=905 nm以及λ2=1 385 nm的远场再现图[75]；(b)利用V型小孔实现的全息的样品SEM图[78]；(c)基于贝里相位纳米棒阵列三维全息示意图[21]；(d)基于贝里相位的高效率反射阵列全息单元结构及其实验测得的远场全息图[77] Fig.9 Hologram based on metasurfaces. (a) an array of metal aperture and the far-field image of metasurface at λ1=905 nm and λ2=1 385 nm, respectively[75]. (b) SEM image of metasurface consisting of V-shaped apertures to realize holography[78]. (c)Schematic of metasurface hologram composed of nanorods array based on Pancharatnam-Berry phase principle[21]. (d)Unit cell of reflect-array metasurfacehologram with high efficiency base on Pancharatnam-Berry phase and the measured image in the far field[77]

在此基础上，为进一步提高全息图信息容量，Huang等人提出了一种基于几何相位的全息图复用方法[79]。通过具有不同相移全息图的线性叠加，可以得到总的合成全息图复振幅为：

Htot(u,v;λ,z,θ)=

(12)

图10 全息图的不同复用方式[79]：(a)可在不同聚焦位置以及旋转角观察全息图的实验装置以及固定观察距离分别在不同圆偏振光入射时所成再现像。(b)同一样品不同z平面再现像；(c)同一样品不同距离以及离轴角观测的再现像 Fig.10 Different forms of holographic multiplexing[79]. (a)Experimental setup for observing the holographic images at separate focus positions and rotational angles and the reconstructions of image for different incident helicity. (b)The measured images for different incident helicity at different z planes. (c)Schematic of the observation for the four encoded objects with separate off-axis angles and reconstruction distances and the experimental reconstruction images

式中，Htot是总合成全息图的复振幅，Hl是单个全息图复振幅或者其复共轭，p为全息图总数，u和v是空间频率，xl和yl分别为每幅图的空间位移。理论上p可以是任何整数，但是实际上由于超颖表面有限的分辨率以及空间带宽积，p不能够过大。根据上述概念，Huang等人[79]实验证明了该复用方法。例如：在同一位置，不同入射圆偏振态下可分别再现“BIT”以及校徽图像(图10(a))；右旋光入射，左旋光出射，在不同成像距离可得到不同再现像(图10(b))；以及在不同离轴角度与成像距离(图10(c))均可以实现全息图复用。这种方法能有效减少加工制造的压力并且大幅提高单一样品的信息容量。

利用惠更斯超颖表面也可以实现纳米全息应用。Zhao等人[31]利用惠更斯超颖表面的原理设计了一种生成全息图的方式，通过在一定范围扫描结构高度与半径，找出介质圆柱适宜的高度与半径以满足相应的表面极化率要求以引入再现全息图所需的相位，并保持振幅一致。为了减少样品制备难度，设计时采用固定介质圆柱半径差来对应相位突变的思路，而不是根据固定相位差选择结构参数。实验最终获得了高达86%的透射效率以及23.6%的光学效率。

近期有关彩色全息的研究逐渐引起了人们的兴趣。Huang等人[80]利用铝纳米棒实现了多色反射式超颖全息。铝作为有着更高等离子体谐振频率的材料，可以将表面等离子谐振频率从可见光区扩展到紫外区[81-82]，这对于生成全彩全息图有着重要意义。通过单一调节铝纳米棒的长度，可实现在不同波长处相位的二元调节，即产生0、π的相位差[80]。这样能够显著降低建造难度，但也造成了多级衍射的问题。通过在一个单元中划分4个子单元，每个子单元对某一波长独立响应，这样在白光入射时便形成了多色全息图。

Wang等人[38]在可见光频段分别实现了消色差以及高色散的介质超颖表面全息应用，其相位操控基本原理是利用贝里相位，通过旋转纳米块的朝向来获得所需相位突变；但Wang等人通过结构设计使得各个纳米块起到半波片的作用以提高偏振转化效率。该超颖表面的一个单元结构同样包含有4个子单元，分别对红、黄和蓝光响应，其中有两个子单元对应蓝光响应以提高效率。在消色差应用中，各子单元拥有相同的相位编码，不同入射光可生成相同的再现像，通过调节红黄蓝3种不同颜色入射光的能量即可获得任意颜色的全息图。而在高色散应用中，各子单元相位分布不一致，针对3种入射波长可分别生成不同图案。Wang等人[38]利用该思路生成了一幅拥有多种色彩的花盆图案。

3.2.3 基于超颖表面的光束轨道角动量操控

涡旋光束是指涡旋中心光强为零且具有螺旋等相位面分布的一种奇异光束[83]。在近轴传播条件下，涡旋光束的波前可用exp(ilφ)描述[84]，l被称为拓扑电荷数，可取分数或者整数，其携带的轨道角动量L=lћ，ћ为普朗克常数。以轨道角动量作为信息载体可显著提高信息容量，在与自旋或者角动量相关的量子信息或粒子操纵等领域有广泛的应用前景[85-86]。通常生成涡旋光束的方法包括空间光调制器、计算全息片、螺旋相位板，达曼光栅等[83]。这些方法所用器件通常较大或者仅适用于窄带范围。利用超颖表面生成涡旋光的方法可以实现超薄化，并能具有宽带的特性。

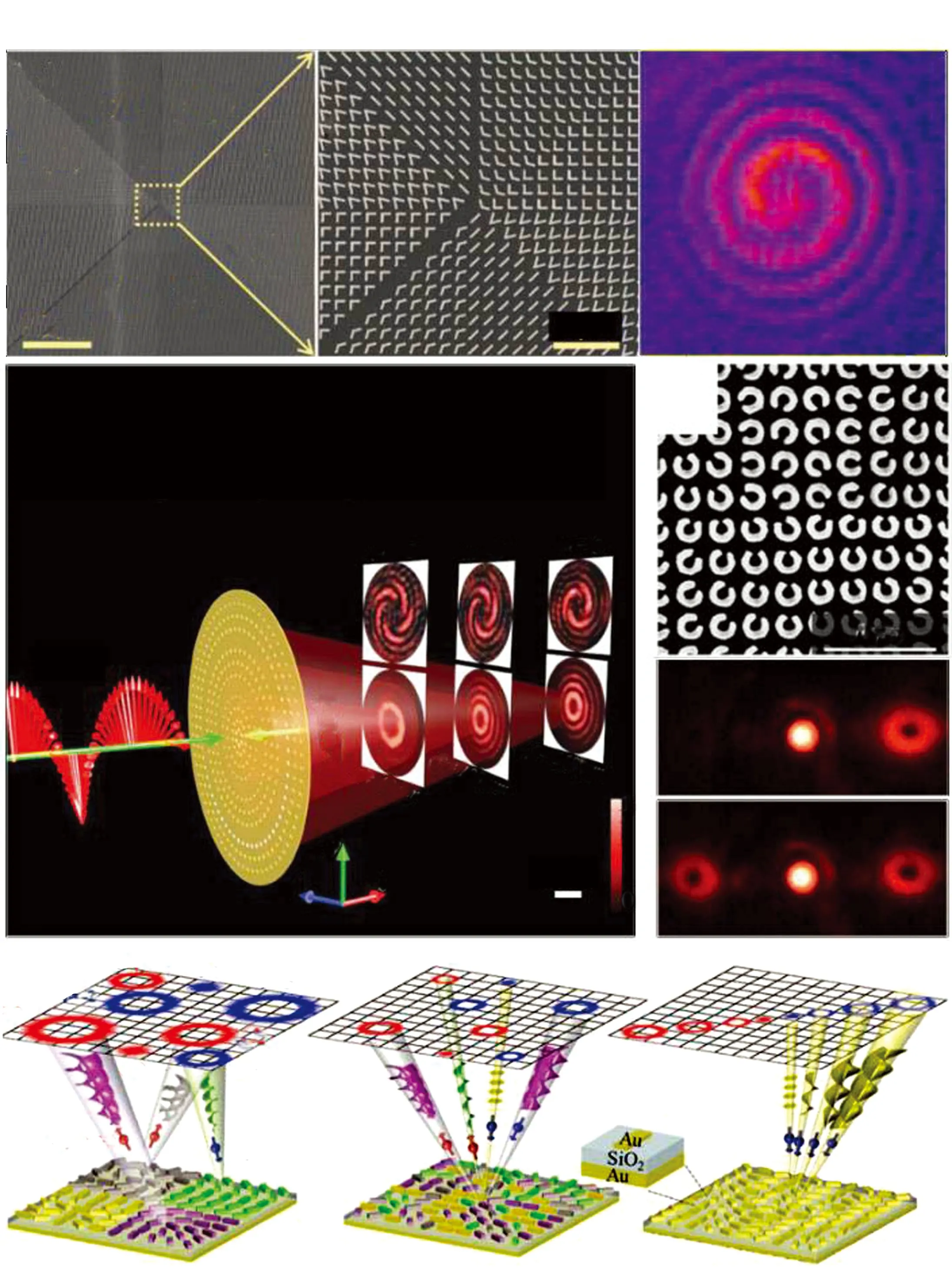
图11 利用超颖表面生成涡旋光：(a)用V型天线超颖表面构成的相位轮廓以及生成的干涉图案[19]；(b)可见光频率空间复用超颖表面示意图[90]；(c)开口环宽带涡旋光生成超颖表面SEM图像以及其左旋光与线偏振光入射下测得的透射图案[87]；(d)从左至右依次为分割式(Segmented)、插入式(Interleaved)与谐波响应(Harmonic Response)超颖表面及其形成的远场强度分布示意图[91] Fig.11 Vortex beam generation based on metasurfaces: (a)A phase profile created using V-shaped antenna metasurfaces and the interference patterns[19]; (b)Schematic of visible-frequency metasurfaces for spatially multiplexing optical vortices[90]; (c)SEM image of the split-ring metasurface which was designed for generating an optical vortex beam and the measured transmitted patterns under the incident beam with left-handed circular polarization and linear polarization, respectively[87]; (d)Schematic of far-field intensity distributions from segmented, interleaved, and harmonic response metasurfaces(from left to right)[91]

Yu等人[19]最早关于V型天线的报道中即验证了利用超颖表面实现涡旋光束的生成，如图11(a)所示。通过将超颖表面四象限按照方位角平分为8份，按方位角的增加每部分增加π/4的相位差，可获得拓扑电荷数l=1的涡旋光，由相位的奇异性可获得中心暗区域[83]。通过与同方向传播的高斯光束共轴传播，可以获得螺旋状干涉条纹；若二者倾斜一定角度，则可获得叉型干涉条纹。基于贝里相位原理的纳米棒[37](图4(c))或者开口环结构[87](图11(c))，均可以实现宽光谱的涡旋光束生成，且在翻转入射圆偏振光时，所得的涡旋光拓扑电荷数正负异号。Yang等人[53]采用介质结构，获得了更高的涡旋光转换效率。对涡旋光的并行处理，包括不同涡旋光本征态的空间复用与解复用[88, 89]等应用，受到了一系列的关注。通过适当结构设计，单个样品可实现同时生成与调控多种涡旋光，实现涡旋光的多路复用。Mehmood等人[90]利用同心圆环分布的纳米棒状孔实现了可见光波段涡旋光复用，该结构可同时生成3种拓扑电荷数的涡旋光并分别在距样品表面不同距离聚焦,如图11(b)。Maguid讨论了超颖表面信息容量的问题[91]。实现复用时，单元结构的表面分布方式,如图11(d),会影响复用时超颖表面的信息容纳能力。

近年来利用达曼光栅的原理制作相位板对涡旋光进行调控受到了人们的关注。在传统的二元相位光栅中，达曼相位编码方法可生成能量均匀的各衍射级次[92]。达曼涡旋光栅(Dammann Optical Vortex Grating)可同时实现不同拓扑电荷数涡旋光的复用与解复用[93]。该结构的设计思路是首先得到各级次不同拓扑电荷数涡旋光表面纯相位叠加，再利用达曼光栅编码方法进行二元相位分布设计。进一步利用达曼空间波带片[94](Spiral Dammann Zone Plate)则可以实现三维涡旋阵列的生成与调控[95-96]。上述方法中，若采用超颖表面，则有望摆脱二元相位带来的限制，降低设计难度。

3.3偏振转换

对于许多现代光电应用，控制电磁波的偏振转换有着重要的意义。由于超颖表面超薄、紧凑以及在设计灵活性上的特点，利用超颖表面实现偏振转换引起了越来越多研究者的兴趣。一般来说，高度的对称性有利于超颖结构单元维持偏振态，而对称性的破缺则可以实现对偏振态的调控。

图12 (a)由V型天线构成的宽波段四分之一波片结构示意图；(b)所得圆偏振光的偏振分析[20]；(c)THz波段实现线偏振到圆偏振转换样品图；(d)实验所得(c)中样品txx和tyy振幅，相位差以及椭偏度[98]；(e)用以实现圆-圆偏振转换的样品示意图；(f)仿真与实验所得透射率[102] Fig.12 (a)Schematic of a broadband quarter-wave plate consisting of V-shaped antennas. (b)State-of-polarization analysis for the obtained circular polarization light[20]. (c)An image of the fabricated sample which produces the linear to circular polarization conversion at THz band. (d) Experimentally measured transmission amplitude, phase retardation, and ellipticity for the sample exhibited in (c)[98]. (e)Schematic of sample to realize asymmetric transmission and polarization conversion. (f)Simulated and measured transmission[102]

Wang等人[97]利用单层单元结构为十字形孔的超颖表面制得了厚度仅为0.29λ的线偏振到圆偏振的转换器件，但这种结构利用了结构的窄带谐振特性，工作带宽很小。利用V型天线，Yu等人[20]设计了一种宽波段四分之一波片，并能产生高质量的圆偏振光，其工作波段可从5 μm覆盖至12 μm，如图12(a)所示。其单元结构包含两个子单元，各个子单元当线偏振光入射时可以产生两束同方向传播的，偏振方向相互正交的线偏振光，并通过子单元之间的错位提供π/2的相位差。除了宽波带的特性，这种结构还利用广义折射现象，使得所获得圆偏振光与原垂直入射光之间存在一定偏折，便于他们之间的分离。其生成圆偏振光的偏振分析如图12(b)所示，可通过旋转置于探测器前的偏振片并测量透射能量获得。

采用双层[98-99]或者多层[100]结构，利用近场或者类法布里-珀罗(Fabry-Pérot)耦合，能有效提高偏振转换效率。Cong等人[98]提出了一种THz波段双层堆叠金属线网格构成的偏振转换器件，该器件可实现线偏振到圆偏振的转换。其第一层的金属线网格与x轴成45°角以使得其垂直方向的透射系数|txx|和|tyy|振幅一致，但是其相位差依赖频率变化；第二层的网格则能补偿这种相位差，使得x、y分量近似保持90°相位差，如图12(c)、12(d)所示。Pfeiffer等人[101-102]设计另一种用三层结构超颖表面实现非对称圆偏振的转化方法，通过构建各层各向异性结构参数，可以实现对整个透射琼斯矩阵的设计，其结构与实验如图12(e)、12(f)所示。这种结构可以在宽波长范围内对于右旋到左旋的透射率可达到50%，而其他透射分量不到2.5%。

图13 基于超颖表面旋光应用。(a)实现线偏振旋转的反射型超颖表面示意图；(b)实现旋光的透射型超颖表面示意图；(c)实验测得反射型结构同偏振与正交偏振反射率；(d)实验测得透射型旋光结构正交偏振透射率和同偏振反射率[103] Fig.13 Linear polarization rotation based on metasurfaces. (a)Schematic of the metasurface to rotate the incident linearly polarized light in reflection; (b)Schematic of the metasurface to rotate the incident linearly polarized light in transmission. (c)Experimentally measured co- and cross-polarized reflection for the reflection type. (d)Experimentally measured cross-polarized transmission and co-polarized reflection for the transmission type[103]

除了线偏振到圆偏振的转换，线偏振态的旋转，即旋光性，也受到一系列关注。Grady等人[103]提出了一种高效的反射与透射阵列如图13所示。反射型线偏振旋转结构由一层金属短线(Cut-Wire)阵列、一层介质中间层以及金属基底层构成，这3层结构形成一种类法布里-珀罗腔的结构，通过设计各结构参数使得同偏振方向达到干涉相消条件，可以实现正交偏振方向达到80%的反射率而同偏振方向反射率极低，如图13(a)、13(c)所示。在金属短线阵列两侧放置方向垂直的光栅结构则可以实现透射型的90°偏振旋转，如图13(b)、13(d)。值得注意的是，在透射型结构中将金属短线阵列换成相位操控结构，则可以在偏振转换的同时发生广义折射等现象，极大提高设计灵活性。利用该思路，超宽频带[104]，工作在可见光波段[105]以及利用介质超颖表面[53]的线偏振旋转得到验证。特别是，若采用介质结构，即一层长方体硅结构与金属基平面中间间隔一层PMMA，由于介质结构的低损耗，可以在近红外波长处实现高达98%的偏振转换效率以及200 nm的带宽[53]。

4 结束语

超颖表面自提出之日起就备受关注。超颖表面将体超颖材料的维度从三维降到二维，有效降低了加工难度和欧姆损耗，不再依赖光在介质中传播带来的相位积累，而是通过平面亚波长天线进行相位调制，使其可称为超薄器件。通过合适的单元结构，超颖表面可以对光场振幅、相位、偏振进行调控，展示了对光场强大的操纵能力，其在光储存、集成光学、量子信息处理等方面具有广阔的应用潜力。本文简要回顾了最近几年发展起来的超颖表面不同调制机理，以及在不同波段有关任意波前调控、偏振转换等方面功能应用。有关超颖表面的研究领域非常广泛，除了本文所述的内容，还包含非线性[106]、电磁吸波材料[107]、表面波全息[108]以及主动可调超颖表面等研究领域。例如，通过物理性质可调材料的引入，研究人员得以实现对表面结构谐振性质的调控，进而实现可调超颖表面。报道较多的途径有利用半导体[109-110]、石墨烯[111-113]或者相变材料[114-115]以实现谐振的调控。强烈的光与物质相互作用可以使得超颖表面仅需要少量可调材料，这有助于实现超颖表面器件的快速调制。综上，超颖表面与生俱来的超薄、紧凑的性质，以及空间逐点光场调控能力，使得其在未来集成化、微型化空间光场调制方面具有重要应用前景。

[1] YU N,CAPASSO F. Flat optics with designer metasurfaces[J].NatureMaterials,2014,13(2):139-150.

[2] CHEN H,TAYLOR A J,YU N. A review of metasurfaces:physics and applications[J].ArXiv:1605.07672,2016.

[3] SMITH D R,PENDRY J B,WILTSHIRE M. Metamaterials and negative refractive index[J].Science,2004,305(5685):788-792.

[4] PENDRY J B,HOLDEN A J,STEWART W J,etal.. Extremely low frequency plasmons in metallic mesostructures[J].PhysicalReviewLetters,1996,76(25):4773-4776.

[5] PENDRY J B,HOLDEN A J,ROBBINS D J,etal.. Magnetism from conductors and enhanced nonlinear phenomena[J].IEEETransactionsonMicrowaveTheoryandTechniques,1999,47(11):2075-2084.

[6] SMITH D R,PADILLA W J,VIER D C,etal.. Composite medium with simultaneously negative permeability and permittivity[J].PhysicalReviewLetters,2000,84(18):4184-4187.

[7] SHELBY R A,SMITH D R,SCHULTZ S. Experimental verification of a negative index of refraction[J].Science,2001,292(5514):77-79.

[8] ZHANG S,FAN W J,PANOIU N C,etal.. Experimental demonstration of near-infrared negative-index metamaterials[J].PhysicalReviewLetters,2005,95(13):137404.

[9] VALENTINE J,ZHANG S,ZENTGRAF T,etal.. Three-dimensional optical metamaterial with a negative refractive index[J].Nature,2008,455(7211):376-379.

[10] XIAO S,CHETTIAR U K,KILDISHEV A V,etal.. Yellow-light negative-index metamaterials[J].OpticsLetters,2009,34(22):3478-3480.

[11] SMITH D R,SCHULTZ S,MARKOS P,etal.. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients[J].PhysicalReviewB,2002,65(19):195104.

[12] SMITH D R,VIER D C,KOSCHNY T,etal.. Electromagnetic parameter retrieval from inhomogeneous metamaterials[J].PhysicalReviewEStatisticalNonlinear&SoftMatterPhysics,2005,71(3):142-154.

[13] PENDRY J B. Negative refraction makes a perfect lens[J].PhysicalReviewLetters,2000,85(18):3966-3969.

[14] FANG N,LEE H,SUN C,etal.. Sub-diffraction-limited optical imaging with a silver superlens[J].Science,2005,308(5721):534-537.

[15] PENDRY J B,SCHURIG D,SMITH D R. Controlling electromagnetic fields[J].Science,2006,312(5781):1780-1782.

[16] LEONHARDT U. Optical conformal mapping[J].Science,2006,312(5781):1777-1780.

[17] HOLLOWAY C L,KUESTER E F,GORDON J A,etal.. An overview of the theory and applications of metasurfaces:the two-dimensional equivalents of metamaterials[J].IEEEAntennasandPropagationMagazine,2012,54(2):10-35.

[18] KILDISHEV A V,BOLTASSEVA A,SHALAEV V M. Planar photonics with metasurfaces[J].Science,2013,339(6125):1232009.

[19] YU N,GENEVET P,KATS M A,etal.. Light propagation with phase discontinuities:generalized laws of reflection and refraction[J].Science,2011,334(6054):333-337.

[20] YU N,AIETA F,GENEVET P,etal.. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces[J].NanoLetters,2012,12(12):6328-6333.

[21] HUANG L,CHEN X,MÜHLENBERND H,etal.. Three-dimensional optical holography using a plasmonic metasurface[J].NatureCommunications,2013,4:2808.

[22] 黄玲玲.基于手性光场作用的超颖表面的相位调控特性及其应用[D].北京:清华大学,2014.

HUANG L L. The phase modulation property of metasurfaces based on chiral field interaction and its applications[D]. Beijing:Tsinghua University,2014.(inChinese)

[23] BHARADWAJ P,DEUTSCH B,NOVOTNY L. Optical antennas[J].AdvancesinOpticsandPhotonics,2009,1(3):438-483.

[24] NOVOTNY L,VAN HULST N. Antennas for light[J].NaturePhotonics,2011,5(2):83-90.

[25] KATS M A,GENEVET P,AOUST G,etal.. Giant birefringence in optical antenna arrays with widely tailorable optical anisotropy[J].ProceedingsoftheNationalAcademyofSciences,2012,109(31):12364-12368.

[26] PFEIFFER C,GRBIC A. Metamaterial Huygens' surfaces:tailoring wave fronts with reflectionless sheets[J].PhysicalReviewLetters,2013,110(19):197401.

[27] PFEIFFER C,EMANI N K,SHALTOUT A M,etal.. Efficient light bending with isotropic metamaterial Huygens' surfaces[J].NanoLetters,2014,14(5):2491-2497.

[28] KIM M,WONG A M H,ELEFTHERIADES G V. Optical Huygens metasurfaces with independent control of the magnitude and phase of the local reflection coefficients[J].PhysicalReviewX,2014,4(4):041042.

[29] WANG Z,SHI J,CHEN J. High-efficiency electromagnetic wave controlling with all-dielectric Huygens'metasurfaces[J].InternationalJ.AntennasandPropagation,2015:1-7.

[30] DECKER M,STAUDE I,FALKNER M,etal.. High-efficiency dielectric Huygens' surfaces[J].AdvancedOpticalMaterials,2015,3(6):813-820.

[31] ZHAO W,JIANG H,LIU B,etal.. Dielectric Huygens'metasurface for high-efficiency hologram operating in transmission mode[J].ScientificReports,2016,6:30613.

[32] Generalized Theory of Interference and its Applications.Part 2:Partially Coherent Pencils[J].ProceedingsofIndianAcademyofSciences,1956,section A,4(6):398-417.

[33] BERRY M V. Quantal phase-factors accompanying adiabatic changes[J].ProceedingsoftheRoyalSocietyofLondonSeriesA-MathematicalandPhysicalSciences,1984,392(1802):45-57.

[34] MENZEL C,ROCKSTUHL C,LEDERER F. An advanced jones calculus for the classification of periodic metamaterials[J].Phys.Rev.A,2010,82(5):53811.

[35] ARMITAGE N P. Constraints on jones transmission matrices from time-reversal invariance and discrete spatial symmetries[J].PhysicalReviewB,2014,90(3):35135.

[36] KANG M,FENG T,WANG H T,etal.. Wave front engineering from an array of thin aperture antennas[J].OpticsExpress,2012,20(14):15882-15890.

[37] HUANG L,CHEN X,M HLENBERND H,etal.. Dispersionless phase discontinuities for controlling light propagation[J].NanoLetters,2012,12(11):5750-5755.

[38] WANG B,DONG F,LI Q,etal.. Visible-frequency dielectric metasurfaces for multiwavelength achromatic and highly dispersive holograms[J].NanoLetters,2016,16(8):5235-5240.

[39] FALCONE F,LOPETEGI T,LASO M,etal.. Babinet principle applied to the design of metasurfaces and metamaterials[J].PhysicalReviewLetters,2004,93(19):197401.

[40] ZENTGRAF T,MEYRATH T P,SEIDEL A,etal.. Babinet′S principle for optical frequency metamaterials and nanoantennas[J].PhysicalReviewB,2007,76(3):033407.

[41] CHEN H T,O'HARA J F,TAYLOR A J,etal.. Complementary planar terahertz metamaterials[J].OptExpress,2007,15(3):1084-1095.

[42] POZAR D M,TARGONSKI S D,SYRIGOS H D. Design of millimeter wave microstrip reflectarrays[J].IEEETransactionsonAntennasandPropagation,1997,45(2):287-296.

[43] 马科斯 玻恩，埃米尔沃尔夫.光学原理——光的传播、干涉和衍射的电磁理论(第七版)[M].北京:电子工业出版社,2009.

BORN M,WOLF E.PrinciplesofOptics:ElectromagneticTheoryofPropagation,InterferenceandDiffractionofLight[M]. Beijing:Electronic Industry Press,2009.(in Chinese)

[44] EVLYUKHIN A B,REINHARDT C,CHICHKOV B N. Multipole light scattering by nonspherical nanoparticles in the discrete dipole approximation[J].PhysicalReviewB,2011,84(23):235429.

[45] EVLYUKHIN A B,REINHARDT C,SEIDEL A,etal.. Optical response features of Si-nanoparticle arrays[J].PhysicalReviewB,2010,82(4):045404.

[46] ZHAO Q,KANG L,DU B,etal.. Experimental demonstration of isotropic negative permeability in a three-dimensional dielectric composite[J].PhysicalReviewLetters,2008,101(2):027402.

[47] VYNCK K,FELBACQ D,CENTENO E,etal.. All-dielectric rod-type metamaterials at optical frequencies[J].PhysicalReviewLetters,2009,102(13):133901.

[48] ZHAO Q,ZHOU J,ZHANG F,etal.. Mie resonance-based dielectric metamaterials[J].MaterialsToday,2009,12(12):60-69.

[49] PENG L,RAN L,CHEN H,etal.. Experimental observation of left-handed behavior in an array of standard dielectric resonators[J].PhysicalReviewLetters,2007,98(15):157403.

[50] GINN J C,BRENER I,PETERS D W,etal.. Realizing optical magnetism from dielectric metamaterials[J].PhysicalReviewLetters,2012,108(9):097402.

[51] CHENG J,ANSARI-OGHOL-BEIG D,MOSALLAEI H. Wave manipulation with designer dielectric metasurfaces[J].OpticsLetters,2014,39(21):6285-6288.

[52] CHONG K E,STAUDE I,JAMES A,etal.. Polarization-independent silicon metadevices for efficient optical wavefront control[J].NanoLetters,2015,15(8):5369-5374.

[53] YANG Y,WANG W,MOITRA P,etal.. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation[J].NanoLetters,2014,14(3):1394-1399.

[54] ARBABI A,HORIE Y,BALL A J,etal.. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays[J].NatureCommunications,2015,6:7069.

[55] ARBABI A,HORIE Y,BAGHERI M,etal.. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission[J].NatureNanotechnology,2015,10(11):937-943.

[56] LIN D,FAN P,HASMAN E,etal.. Dielectric gradient metasurface optical elements[J].Science,2014,345(6194):298-302.

[57] AIETA F,GENEVET P,YU N,etal.. Out-of-plane reflection and refraction of light by anisotropic optical antenna metasurfaces with phase discontinuities[J].NanoLetters,2012,12(3):1702-1706.

[58] ZHANG X,TIAN Z,YUE W,etal.. Broadband terahertz wave deflection based on c-shape complex metamaterials with phase discontinuities[J].AdvancedMaterials,2013,25(33):4567-4572.

[59] SUN S,HE Q,XIAO S,etal.. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves[J].NatureMaterials,2012,11(5):426-431.

[60] SUN S,YANG K,WANG C,etal.. High-efficiency broadband anomalous reflection by gradient meta-surfaces[J].NanoLetters,2012,12(12):6223-6229.

[61] 金国藩,严瑛白,邬敏贤.二元光学[M].北京:国防工业出版社,1998.

JIN G F,YAN Y B,WU M X.BinaryOptics[M]. Beijing:National Defense Industry Press,1998.(inChinese)

[62] MARCHAND E W.GradientIndexOptics[M]. New York:New York Academic Press,1978.

[63] AIETA F,GENEVET P,KATS M A,etal.. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces[J].NanoLetters,2012,12(9):4932-4936.

[64] LI X,XIAO S,CAI B,etal.. Flat metasurfaces to focus electromagnetic waves in reflection geometry[J].OpticsLetters,2012,37(23):4940-4942.

[65] NI X,ISHII S,KILDISHEV A V,etal.. Ultra-thin, planar, babinet-inverted plasmonic metalenses[J].Light:Science&Applications,2013,2(4):e72.

[66] KUZNETSOV S A,ASTAFEV M A,BERUETE M,etal.. Planar holographic metasurfaces for terahertz focusing[J].ScientificReports,2015,5:7738.

[67] CHEN X,HUANG L,M HLENBERND H,etal.. Dual-polarity plasmonicmetalens for visible light[J].NatureCommunications,2012,3:1198.

[68] PORS A,NIELSEN M G,ERIKSEN R L,etal.. Broadband focusing flat mirrors based on plasmonic gradient metasurfaces[J].NanoLetters,2013,13(2):829-834.

[69] KHORASANINEJAD M,CHEN W T,DEVLIN R C,etal.. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging[J].Science,2016,352(6290):1190-1194.

[70] KHORASANINEJAD M,AIETA F,KANHAIYA P,etal.. Achromatic metasurface lens at telecommunication wavelengths[J].NanoLetters,2015,15(8):5358-5362.

[71] 谢敬辉，廖宁放，曹良才.傅里叶光学与现代光学基础[M].北京:北京理工大学出版社,2007.

XIE J H,LIAO N F,CAO L C.FundamentalsofFourierOpticsandContemporaryOptics[M]. Beijing:Beijing Institute of Technology Press,2007.(inChinese)

[72] SLINGER C,CAMERON C,STANLEY M. Computer-generated holography as a generic display technology[J].Computer,2005,38(8):46-53.

[73] KELLY D P,MONAGHAN D S,PANDEY N,etal.. Digital holographic capture and optoelectronic reconstruction for 3D displays[J].InternationalJ.DigitalMultimediaBroadcasting,2010,2010:1-14.

[74] GENG J. Three-dimensional display technologies[J].AdvancesinOpticsandPhotonics,2013,5(4):456-535.

[75] WALTHER B,HELGERT C,ROCKSTUHL C,etal.. Spatial and spectral light shaping with metamaterials[J].AdvancedMaterials,2012,24(47):6300-6304.

[76] NI X,KILDISHEV A V,SHALAEV V M. Metasurface holograms for visible light[J].Nat.Comm ,2013,4:2807.

[77] ZHENG G,M HLENBERND H,KENNEY M,etal.. Metasurface holograms reaching 80% efficiency[J].NatureNanotechnology,2015,10(4):308-312.

[78] NI X,KILDISHEV A V,SHALAEV V M. Metasurface holograms for visible light[J].NatureCommunications,2013,4:2807.

[79] HUANG L,M HLENBERND H,LI X,etal.. Broadband hybrid holographic multiplexing with geometric metasurfaces[J].AdvancedMaterials,2015,27(41):6444-6449.

[80] HUANG Y,CHEN W T,TSAI W,etal.. Aluminum plasmonic multicolor meta-hologram[J].NanoLetters,2015,15(5):3122-3127.

[81] KNIGHT M W,KING N S,LIU L,etal.. Aluminum for plasmonics[J].ACSNano,2014,8(1):834-840.

[82] KNIGHT M W,LIU L,WANG Y,etal.. Aluminum plasmonic nanoantennas[J].NanoLetters,2012,12(11):6000-6004.

[83] PADGETT M,COURTIAL J,ALLEN L. Light's orbital angular momentum[J].PhysicsToday,2004,57(5):35-40.

[84] ALLEN L,BEIJERSBERGEN M W,SPREEUWR,etal.. Orbital angular-momentum of light and the transformation of Laguerre-Gaussian laser modes[J].PhysicalReviewA,1992,45(11):8185-8189.

[85] MOLINA-TERRIZA G,TORRES J P,TORNER L. Twisted photons[J].NaturePhysics,2007,3(5):305-310.

[86] VERBEECK J,TIAN H,SCHATTSCHNEIDER P. Production and application of electron vortex beams[J].Nature,2010,467(7313):301-304.

[87] ZENG J,LI L,YANG X,etal.. Generating and separating twisted light by gradient rotation split-ring antenna metasurfaces[J].NanoLetters,2016,16(5):3101-3108.

[88] LI S,WANG J. Simultaneous demultiplexing and steering of multiple orbital angular momentum modes[J].ScientificReports,2015,5:15406.

[89] REN H,LI X,ZHANG Q,etal.. On-chip noninterference angular momentum multiplexing of broadband light[J].Science,2016,352(6287):805-809.

[90] MEHMOOD M Q,MEI S,HUSSAIN S,etal.. Visible-frequency metasurface for structuring and spatially multiplexing optical vortices[J].AdvancedMaterials,2016,28(13):2533-2539.

[91] MAGUID E,YULEVICH I,VEKSLER D,etal.. Photonic spin-controlled multifunctional shared-aperture antenna array[J].Science,2016,352(6290):1202-1206.

[92] ZHANG N,YUAN X C,BURGE R E. Extending the detection range of optical vortices by dammann vortex gratings[J].Opt.Lett.,2010,35(20):3495-3497.

[93] LEI T,ZHANG M,LI Y,etal.. Massive individual orbital angular momentum channels for multiplexing enabled by dammann gratings[J].Light:Science&Applications,2015,4(3):e257.

[94] YU J,ZHOU C,JIA W,etal.. Generation of dipole vortex array using spiral dammann zone plates[J].Appl.Opt.,2012,51(28):6799-6804.

[95] YU J,ZHOU C,JIA W,etal.. Three-dimensional dammann array[J].Appl.Opt.,2012,51(10):1619-1630.

[96] YU J,ZHOU C,JIA W,etal.. Three-dimensional dammann vortex array with tunable topological charge[J].Appl.Opt.,2012,51(13):2485-2490.

[97] WANG D,GU Y,GONG Y,etal.. An ultrathin terahertz quarter-wave plate using planar babinet-inverted metasurface[J].OpticsExpress,2015,23(9):11114-11122.

[98] CONG L,XU N,GU J,etal.. Highly flexible broadband terahertz metamaterial quarter-wave plate[J].Laser&PhotonicsReviews,2014,8(4):626-632.

[99] LI Y,ZHANG J,QU S,etal.. Achieving wide-band linear-to-circular polarization conversion using ultra-thin bi-layered metasurfaces[J].J.AppliedPhysic,2015,117(4):44501.

[100] SUN W,HE Q,HAO J,etal.. A transparent metamaterial to manipulate electromagnetic wave polarizations[J].OpticsLetters,2011,36(6):927-929.

[101] PFEIFFER C,GRBIC A. Bianisotropic metasurfaces for optimal polarization control:analysis and synthesis[J].PhysicalReviewApplied,2014,2(4):044011.

[102] PFEIFFER C,ZHANG C,RAY V,etal.. High performance bianisotropicmetasurfaces:asymmetric transmission of light[J].PhysicalReviewLetters,2014,113(2):023902.

[103] GRADY N K,HEYES J E,CHOWDHURY D R,etal.. Terahertz metamaterials for linear polarization conversion and anomalous refraction[J].Science,2013,340(6138):1304-1307.

[104] CHEN H,WANG J,MA H,etal.. Ultra-wideband polarization conversion metasurfaces based on multiple plasmon resonances[J].J.AppliedPhysics,2014,115(15):154504.

[105] DAI Y,REN W,CAI H,etal.. Realizing full visible spectrum metamaterial half-wave plates with patterned metal nanoarray/insulator/metal film structure[J].OpticsExpress,2014,22(7):7465-7472.

[106] MINOVICH A E,MIROSHNICHENKO A E,BYKOV A Y,etal.. Functional and nonlinear optical metasurfaces[J].Laser&PhotonicsReviews,2015,9(2):195-213.

[107] CUI Y,HE Y,JIN Y,etal.. Plasmonic and metamaterial structures as electromagnetic absorbers[J].Laser&PhotonicsReviews,2014,8(4):495-520.

[108] GENEVET P,CAPASSO F. Holographic optical metasurfaces:a review of current progress[J].ReportsonProgressinPhysics,2015,78(2):24401.

[109] GU J,SINGH R,LIU X,etal.. Active control of electromagnetically induced transparency analogue in terahertz metamaterials[J].NatureCommunications,2012,3:1151.

[110] WATTS C M,SHREKENHAMER D,MONTOYA J,etal.. Terahertz compressive imaging with metamaterial spatial light modulators[J].NaturePhotonics,2014,8(8):605-609.

[111] HUIDOBRO P A,KRAFT M,MAIER S A,etal.. Graphene as a tunable anisotropic or isotropic plasmonic metasurface[J].ACSNano,2016,10(5):5499-5506.

[112] DABIDIAN N,DUTTA-GUPTA S,KHOLMANOV I,etal.. Experimental demonstration of phase modulation and motion sensing using graphene-integrated metasurfaces[J].NanoLetters,2016,16(6):3607-3615.

[113] LI Z,YU N. Modulation of mid-infrared light using graphene-metal plasmonic antennas[J].AppliedPhysicsLetters,2013,102(13):131108.

[114] KATS M A,BLANCHARD R,GENEVET P,etal.. Thermal tuning of mid-infrared plasmonic antenna arrays using a phase change material[J].OpticsLetters,2013,38(3):368-370.

[115] YIN X,SCH FERLING M,MICHEL A U,etal.. Active chiral plasmonics[J].NanoLetters,2015,15(7):4255-4260.

Theprincipleandresearchprogressofmetasurfaces

LI Tian-you, HUANG Ling-ling*, WANG Yong-tian

(SchoolofOptoelectronics,BeijingInstituteofTechnology,Beijing100081,China)

Metasurfaces, a specific type of subwavelength-scale two-dimensional(2D) array, have shown great flexibilities to control the light field. Metasurfaces possess the unique advantages of ultrathin, low-loss and easy fabrication, therefore attract immense attentions and show broad prospects for applications. This paper reviews recent progress in the physics of metasurfaces and the applications for generalized refraction and reflection, polarization conversion, controlling the orbit angular moment of light and computer generated holography(CGH). Due to the extra design freedom and powerful functionality, metasurfaces allow the possibility to substitute the conventional optical components in a variety of applications. In the future, novel types of metasurfaces with broadband, high efficiency, multi-task and active tunability are still highly desired and of great value.

metasurface;polarization conversion;orbit angular momentum;computer generated holography(CGH)

TP394.1； TH691.9

A

10.3788/CO.20171005.0523

李天佑(1994—)，男，湖南岳阳人，硕士研究生，2015年于北京理工大学获得学士学位，主要从事超颖表面功能器件方面的研究。E-mail:19940416@bit.edu.cn

黄玲玲(1986—)，女，福建莆田人，特别研究员，博士生导师，北京市科技新星，2009年于天津大学、南开大学获得双学士学位，2014年于清华大学获得博士学位，主要从事超颖表面物理机制与功能器件方面的研究。E-mail:huanglingling@bit.edu.cn

王涌天(1957—)，男，教授、博导，“长江学者奖励计划”特聘教授，主要从事头盔立体显示、增强现实虚实融合显示、体三维和全息三维显示及其相关光学系统设计方面的研究。E-mail:wyt@bit.edu.cn

2017-05-11；

2017-08-13

国家自然科学基金资助项目(No.61505007)；北京市科技新星计划项目资助

Supported by National Natural Science Foundation of China(No.61505007)；Beijing Nova Program(No.Z171100001117047)

2095-1531(2017)05-0523-18

*Correspondingauthor,E-mail:huanglingling@bit.edu.cn