基于反共振原理的管路吸振器调谐方法

杨 恺，张针粒

（武汉第二船舶设计研究所，武汉 430205）

基于反共振原理的管路吸振器调谐方法

杨 恺，张针粒

（武汉第二船舶设计研究所，武汉 430205）

针对船用管路线谱振动传递的抑制问题，提出一种基于反共振原理的管路吸振器调谐方法。该方法利用吸振器带来的反共振物理特性，通过调谐动力吸振器固有频率，改变管路振动传递函数的反共振区域，使需要抑制的线谱频率处于该区域，从而改变管路振动传递特性，实现振动抑制。首先，介绍采用动力吸振器抑制管路线谱振动传递的策略。随后，针对船用管路提出动力吸振器的结构形式及其安装方式。其次，利用结构波理论，阐述基于反共振原理的调谐方法以及调谐步骤。最后，通过实验验证吸振器对某实船管路线谱振动传递的抑制性能。实验结果显示，调谐后的吸振器引入了反共振区域，有效降低了该线谱振动的传递。

振动与波；反共振；动力吸振器；线谱振动；结构波；管路

舰船在低速航行时，低频强线谱机械振动对舰船的辐射噪声能量贡献巨大。尽管目前国内外采用浮筏减震技术实现了对机械设备振动的有效隔离[1]，但是连接机械设备的管路系统却成为了低频振动噪声的主要传递路径，甚至某些通海管路直接成为舰船主要的辐射噪声源，严重影响舰船的隐身性能。

采用动力吸振技术是一种抑制管路低频线谱振动传递的有效解决途径。通过在管路结构上安装动力吸振器（简称吸振器），利用吸振器在自身共振时对被控结构产生反作用力的原理，抑制管路的振动[2–3]。管路结构的振动抑制问题可视为柔性结构的振动抑制问题。针对柔性结构，国外学者开展了大量的动力吸振技术研究[4–8]。例如，文献[4–7]基于结构波理论计算动力吸振器的设计参数，以实现对梁结构的振动抑制；文献[8]将管路结构视为无限梁结构，利用结构波理论建立了吸振器在管路结构的插入损失计算模型。上述研究工作将被控结构系统简化为无限梁结构，建立对应的数学模型，利用数学模型推导吸振器的物理参数。然而，在实际工程应用中，管路系统通常复杂，且包含诸多管路附件（例如阀门），基于简化数学模型推导出的吸振器设计参数难以适用实际工程需求。此外，舰船上管路系统众多，若通过理论建模的方式针对每一个管路系统进行吸振器的设计，将耗费巨大的设计时间。因此，针对管路系统的低频线谱振动传递抑制问题，亟需提出一种通用性好、简单可靠的吸振器及其调谐方法。

文献[9]的研究结果表明，吸振器会在被控柔性结构的频响函数中引入“反共振”特性。文献[10]则针对欧拉伯努利梁的抑振问题，讨论了吸振器的反共振特性。文献[11]将动力吸振器的反共振特性应用于管路结构抑振，研究结果显示，吸振器能有效地抑制管路结构在吸振器安装位置的前两阶共振响应。然而，与文献[11]的研究不同，本文的研究目标是抑制管路系统低频线谱振动（非共振响应）的传递，而不是抑制吸振器安装位置的振动。此外，本文将提出一种通用性良好的吸振器调谐方法，避免通过复杂的数学建模计算吸振器的物理参数，以便于工程应用。该方法利用力锤实验法测得安装吸振器后管路结构目标测点的振动传递函数，通过调整吸振器的固有频率，改变传递函数中的“反共振”区域分布，使需要抑制的振动频率处于该区域，从而降低该目标测点的振动响应，实现对振动传递的抑制。

本文的结构如下：首先将给出基于吸振器的管路振动传递抑制策略。随后，本文针对船用管路系统提出了吸振器的设计及其安装方式。其次，将阐述基于反共振原理的吸振器调谐方法。最后，针对某实船管路的低频线谱抑制问题，对本文方法的有效性进行了实验验证。

1 管路吸振器用于线谱振动传递抑制

如图1所示，在管路结构上安装多个吸振器，以抑制振动在管路结构上的传递。

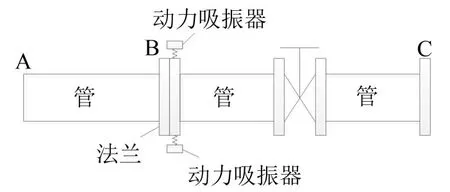
图1 管路吸振器用于抑制管路振动传递的示意图

其中，与管路连接的某水泵处于A点，水泵的运行会激起管路的振动，并通过管路将振动传递至船体。图示的B点为吸振器的安装点，C点为管路连接船体的位置。由于通常情况下，管路结构上会铺设阻尼等材料，因此为不破坏阻尼材料，选择管路的连接法兰作为吸振器管卡结构的安装位置。

管路吸振器安装在管路激励源和目标测点之间。由于舰船空间有限，限制了单个吸振器的体积、重量，因此采用在同一位置布置多个相同的吸振器，使多个吸振器同时对管路产生吸振作用，增加吸振效果。

2 管路吸振器结构形式

为便于调谐吸振器的固有频率，设计了悬臂梁形式的吸振器。如图2所示，该悬臂梁形式的吸振器由质量块和带螺纹的悬臂杆（以下简称螺纹杆）组成。吸振器的端部也攻有螺纹，为吸振器与管路的安装接口。悬臂梁动力吸振器在管路上的安装方式如下：设计与管路外径匹配的管卡结构，该管卡结构上有均布的螺纹孔，螺纹孔轴向与管路轴向平行，螺纹孔尺寸与吸振器端部螺纹匹配。将管卡结构卡紧在管路上，并将吸振器端部通过螺纹连接方式与管卡结构固联，从而实现吸振器在管路上的安装。当螺纹杆的端部安装在管路上，其1阶振动为弯曲振动。质量块的振动引起螺纹杆的变形，从而在端部产生交变剪力，该剪力即为吸振器对管路的反作用力。

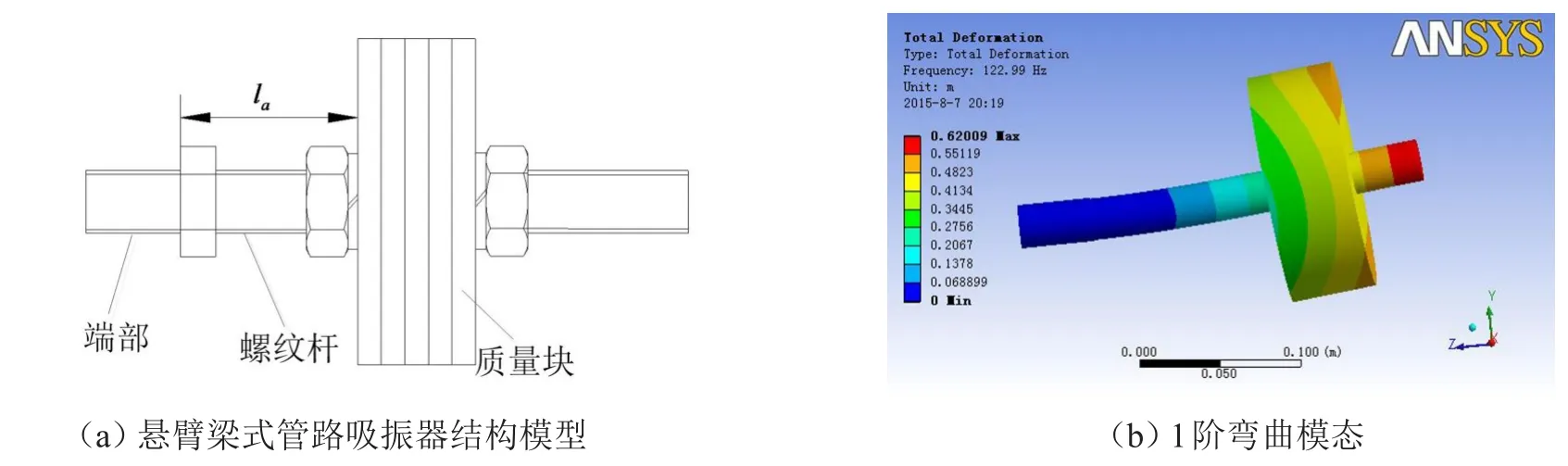
图2 悬臂梁式管路吸振器结构及其1阶弯曲模态

图2中所示的la为质量块在螺纹杆上的位置，当该吸振器端部固定时，即成为带集中质量的悬臂梁结构，假设相对螺纹杆长度la而言，质量块的尺寸可以忽略，此时螺纹杆提供的近似刚度为[12]

式中Ea为弹性模量，Ia为螺纹杆截面惯性矩。从式（1）可以看出，通过改变la，可改变该吸振器的固有频率。吸振器的刚度ka会随着la的增加单调连续减少，可通过实测的传感器信号来调整质量块la位置，从而改变吸振器的固有频率。

3 基于反共振原理的吸振器调谐方法

本节将基于结构波理论对管路振动传递规律展开分析，阐述基于反共振原理的吸振器调谐方法。

3.1 透射波幅值推导

为便于理论推导，将管段视为无限长梁结构，利用结构波理论推导力学关系[7，13]，该理论常用于研究柔性结构振动能量的传递问题[14–15]。图3为图1所示系统的力学模型。在管路上建立坐标系，x指向振动传递方向。设备处于x=-l位置，产生的激励力记为其中ω为激励频率，Fe为激励力振幅，j为单位虚数。在x=0处共安装了n个吸振器，各吸振器对管路的反作用力记为激励引起管路振动，产生弯曲波，弯曲波近场（随着x的增大衰减）和远场（随着x的变化周期振荡）振幅分别为

图3 动力学模型

该弯曲波经过距离为l的管段传递至B点（x=0），近场和远场振幅变为由于吸振器对管路产生的反作用力，造成B点波传递出现了“间断”，导致在x＜0的方向产生了反射弯曲波和透射弯曲波。其中反射波近场和远场振幅分别为和b-；透射波的近场和远场振幅分别

因此，消除时间分量ejωt后的管路弯曲振动位移可表示为

其中，根据文献[7]有

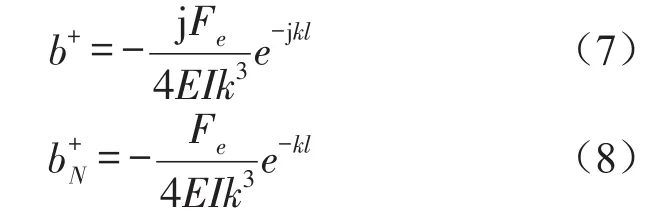
根据连续性条件

式中Ki为第i个吸振器产生的动刚度

其中mai、kai和ηi分别为第i个吸振器的质量、刚度和损耗因子。根据式（9），整理得到

为使吸振器能最大程度地抑制线谱振动，需要其阻尼非常小[2]，因此假设损耗因子ηi=0。假设各吸振器的质量mai均相同（令mai=ma），通过调整各吸振器刚度使得kai=ka，并定义无量纲调谐系数式（11）可以简化为

式中

式中f为频率/Hz。

3.2 理论分析

根据式（12）可知，当调整调谐系数Ω，可以降低透射波远场和近场振幅，从而降低测点C的振动

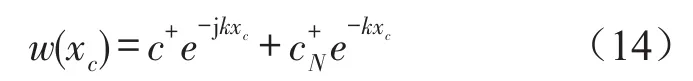
根据式（12）和（14），为了使|w(xc)|最小，即振动位移最小，可计算得到最优调谐系数Ωopt在不同频率处随吸振器安装位置和测点位置的变化关系。图4分别给出了当激励频率为20 Hz、70 Hz和120 Hz时，使|w(xc)|最小的最优调谐系数Ωopt与安装位置l和测点位置xc的关系。仿真中，管路线密度ρA=89.645kg/m，弯曲刚度EI=6.735 7×106N/m，因此，

结果显示，针对每个激励频率f，当吸振器远离激励源、以及目标测点远离吸振器时，最优调谐系数Ωopt会增大（例如图4(c)所示，Ωopt从Ωopt=1逐渐增大到Ωopt=1.02），而且随着激励频率f的增大，Ωopt的增大趋势也更加明显。根据图4所示的结果，如果吸振器布置在激励源附近（l→0）、或者吸振器布置在目标测点附近（xc→0），则最优调谐系数Ωopt→1，此时将吸振器的固有频率调谐至激励频率，即能获得最优抑振效果。

对于图4所示的变化规律，可通过如下的定性分析解释：

（1）当激励源远离吸振器安装位置（l＞＞1）

在该情况下，为了使|w(xc)|最小，则最优调谐系数满足此时，|w(xc)|→0 。这表明，最优调谐系数Ωopt与测点距离xc密切相关，随着xc的增大，Ωopt以指数速率趋向于同时，根据式（13），γ与激励频率的开方成正比，导致激励频率越高，Ωopt偏离1的程度越大。若测点非常接近吸振器安装位置（xc≈0），则最优调谐系数Ωopt=1。

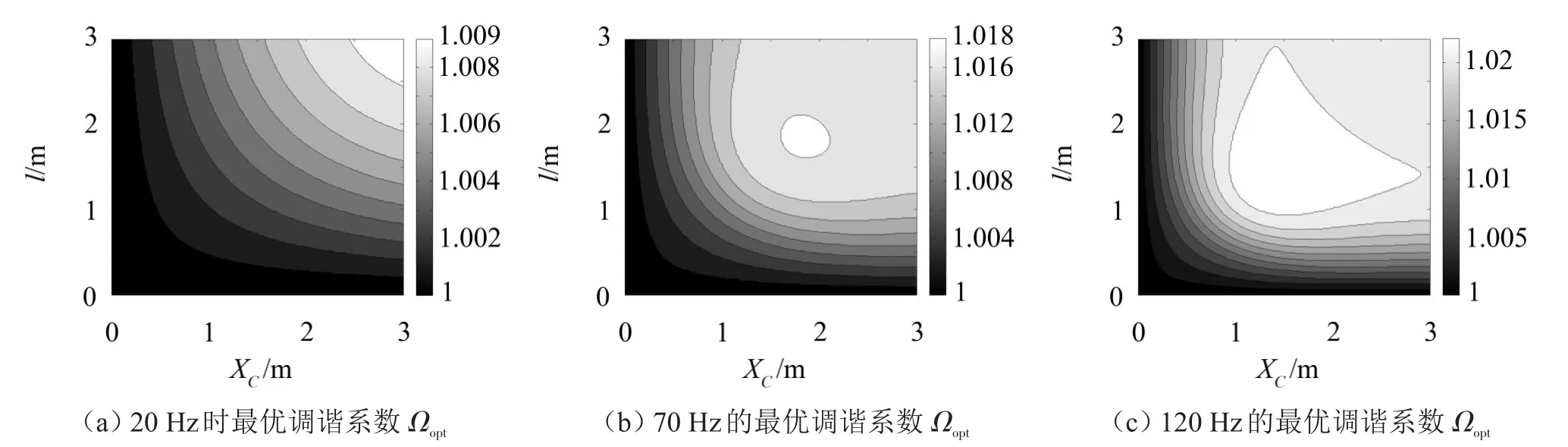
图4 不同激励频率下最优调谐系数Ωopt与安装位置的关系

（2）当激励源接近吸振器安装位置（l≈0）

从上面的分析可以看出，测点位置和激励源位置对调谐系数的影响非常大。尤其对于情况（1），需要同时考虑远场和近场幅值，才能得到最优调谐系数Ω。然而实际的管路系统与上述理论模型存在较大误差，不易确定激励源与吸振器安装位置的准确间距l，难以利用式（12）准确求得调谐系数。因此，必须采用一套基于实验测试的方法来调谐吸振器的固有频率。

3.3 基于反共振原理的吸振器调谐方法

图5给出了针对120 Hz频率采取调谐系数Ωopt=1时，测点振动位移|w(xc)|的频响曲线。其中，为方便分析，激励力满足Fe=4EI，其他仿真参数与图4一致，在图5（a）中，吸振器安装位置l=0，而测点C位置xc发生变化，图5（b）中，测点C的位置xc=1，吸振器安装位置发生变化。

图5（a）结果显示，频响曲线中在120 Hz均出现了“反共振区域”，且调谐系数Ω=1时，无论测点位置xc如何变化，|w(xc)|在120 Hz处最小。而图5（b）结果显示，随着吸振器安装位置l增加，激励源的远场效应变得明显（即e-kl→0）导致反共振点逐渐从120 Hz向高频偏移，这表明，调谐系数Ω=1不再使|w(xc)|最小。尽管如此，使用调谐系数Ω=1，与未安装吸振器的情况对比，|w(xc)|也会减小，原因可以由式（15）解释

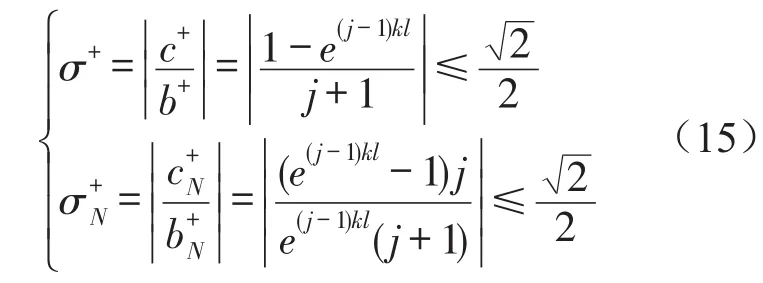
图5 测点位置在120 Hz附近的频响曲线

为在实际应用中准确地调谐吸振器，使Ω=1，可以通过力锤实验法敲击管路吸振器的安装位置，测得敲击点传递至测点的传递函数曲线。在此情况下，敲击位置即为假想的激励源，满足条件l=0，因此其反共振点对应的频率即是Ω=1对应的频率。调整吸振器参数ka，移动该反共振频率，使其接近激励频率，则能显著降低测点的振动。

吸振器的布置及调谐方法总结如下：

（1）吸振器尽可能安装在离激励源近的位置；

（2）将吸振器安装在管路上，利用力锤锤击吸振器安装位置，求得敲击位置至测点的传递函数曲线；

（3）观察传递函数曲线，会发现在激励频率附近出现了反共振区域。若反共振点频率高于线谱频率，则调整吸振器质量块，增大其在悬臂杆上的偏移位置la，以此降低吸振器的刚度ka，从而降低反共振点频率，反之则减小偏移位置la，提高反共振频率。直到反共振频率为需要抑制的线谱频率，此时调谐系数Ω=1。

4 实验验证

4.1 实验台架及实验过程

如图6(a)所示，设计并研制了一套悬臂梁式吸振器和管卡结构，如图6(b)所示将吸振器安装在某船用管路法兰上。实验中共安装了三个吸振器，各吸振器的质量块均为7.6 kg，悬臂杆为M27螺纹杆。在本实验中，当水泵运转时，导致管路结构产生与其运转频率一致的线谱振动，该振动会沿着管路传递至与船体相连的C点，从而引起船体产生对应线谱的振动。通过反共振原理调谐吸振器，阻碍该线谱振动向船体的传递。

图6 实验原理样机和实验过程

实验过程如下：利用力锤敲击管路吸振器的安装位置，利用Pulse测试系统测得敲击点至C点的传递函数，确认吸振器引入的反共振区域。调整吸振器质量块位置，使传递函数反共振频率恰好为水泵的运转频率。

当吸振器质量块的偏移位置分别为la=73mm，la=76mm，la=73mm时，敲击点至测点C的传递函数如图7所示。

图7中，横坐标是以水泵运转频率为基准的归一化频率（即ω=1为水泵的运转频率），结果显示，当吸振器调谐完成后，在ω=1位置，出现了明显的反共振区域。

图7 安装吸振器前后测得的传递函数曲线

4.2 实验结果

运行水泵，利用Pulse测试系统采集测点C的加速度振级，结果如图8所示。

图8 安装吸振器前后测得的目标测点加速度振级

结果显示，当安装吸振器后，在水泵的运转频率ω=1处，目标测点的振级由97.3 dB降至90.8 dB，降幅6.5 dB。该结果表明，基于反共振理论的吸振器调谐方法能够有效抑制管路低频线谱的振动传递。

5 结语

针对管路线谱振动传递抑制问题，本文提出了一种基于反共振原理的吸振器调谐方法，并通过实验验证了该方法的有效性，得出了以下结论：

（1）该方法基于实验测得的传递函数调整吸振器固有频率，无需对管路系统进行动力学建模。

（2）通过调谐动力吸振器可使管路测点传函在激励频率处出现新的反共振区域，从而有效降低了目标测点的振动响应。

[1]余永丰，庞天照，关珊珊，等.大型浮筏隔振系统筏架耦合振动研究[J].噪声与振动控制，2010，30(5)：56-59.

[2]JP HARTOG.Mechanicalvibration[M].Mechanical Vibrations(4 th ed.)[M].McGraw-Hill,New York,1956.

[3]JQ SUN,MR JOLLY,MA NORRIS.Passive,adaptive and active tuned vibration absorbers-a survey[J].Transactions of the ASME,Special 50 th Anniversary Design Issue,1995,117(117):234-242

[4]MJ BRENNAN.Control of flexural waves on a beam using a tunable vibration neutraliser[J].Journal of Sound and Vibration,1998,222(3):389-407.

[5]Y GAO,MJ BRENNAN,F SUI.Control of flexural waves on a beam using distributed vibration neutralisersl[J].Journal of Sound and Vibration,2011,330(12):501-514.

[6]H Salleh,MJ Brennan.Control of flexural waves on a beam using a vibration neutraliser:effects of different attachment configurations[J].Journal of Sound and Vibration,2007,303(3-5):501-514.

[7]HM EL-KHATIB,BRMACE,MJBRENNAN.Suppression of bending waves in a beam using a tuned vibration absorber[J].Journal of Sound and Vibration,2005,288(4):1157-1175.

[8]王文初，尹志勇，陈科，等.新型三向管路动力吸振器设计方法研究[J].船舶力学，2015，19(1-2)：191-197.

[9]BP WANG,L KITIS,WD PILKEY,et al.Synthesis of dynamic vibration absorber[J].Journal of Vibration,Acoustics,Stress,and Reliablity in Design,1985,107(2):161-166.

[10]PD CHA,JM RINKER.Enforcing nodes to suppress vibration along a harmonically forced damped eulerbernoulli beam[J].Journal of Vibration and Acoustics,2012,134(5):051010-1-051010-10.

[11]周笛，陈果，刘明华，等.一种可调谐式的管路动力吸振器研究与实验验证[J].噪声与振动控制，2015，35(2)：217-221.

[12]张针粒，杨恺，李强.悬臂式动力吸振器设计方法[J].噪声与振动控制，2017，37(1)：158-162.

[13]L CREMER,M HECKL.Structure-borne sound[M].Berlin,Springer-Verlag,1988.

[14]DING L,ZHU H P,WU L.Effects of axial load and structural damping on wave propagation in periodic timoshenko beams on elastic foundations under moving loads[J].Physics Letters A,2016,380(31-32):2335-2341.

[15]MORSBØL J,SOROKIN S V.Elastic wave propagation in curved flexible pipes[J].International Journal of Solids and Structures,2015,75-76:143-155.

Tuning Method for Pipeline VibrationAbsorbers Based onAnti-resonance Principle

YANG Kai,ZHANG Zhen-li
(Wuhan the Second Research Institute of Ships,Wuhan 430205,China)

The problem of line spectrum vibration transmission abatement of marine pipelines is studied.A tuning method for pipeline vibration absorbers(PVA)is proposed based on anti-resonance principle.In this method,the antiresonance feature of PVA is applied to change the anti-resonance zone of vibration transmission function of the pipeline by tuning the PVA natural frequency,so that the anti-resonance zone can cover the line spectrum frequency which is to be suppressed.Hence,the pipeline vibration transmission feature is improved and the vibration reduction is realized.First of all,the strategy of using PVAs for line spectrum vibration transmission reduction of pipeline is introduced,and the design of the PVAs and their installation for marine pipeline is presented.Then,the tuning method based on anti-resonance principle and tuning steps by means of structural wave theory is interpreted.Finally,the experimental validation of using PVAs to reduce the line spectrum vibration with a certain frequency is presented.Results show that this method can effectively reduce the line spectrum vibration transmission for the pipelines.

vibration and wave;anti-resonance;dynamic vibration absorber;line spectrum vibration;structural wave;pipeline

TB123

A

10.3969/j.issn.1006-1355.2017.05.012

1006-1355(2017)05-0055-06

2017-02-09

杨恺（1986－），男，武汉市人，博士，工程师，主要研究方向为结构主被动振动控制研究。

E-mail:yangkaibuaa@163.com