改进变步长快速迭代收缩阈值算法

陈少利，杨 敏

(南京邮电大学 自动化学院，江苏 南京 210023)

改进变步长快速迭代收缩阈值算法

陈少利，杨 敏

(南京邮电大学 自动化学院，江苏 南京 210023)

图像复原问题是图像处理中的一项重要研究内容，解决图像复原问题，往往涉及到大量的数据集和未知信息。为了解决此类高维数据优化问题，前向后向算法提供了简洁、实用的方法。快速迭代收缩阈值算法是在前向后向算法的基础上加入了全局加速算子，一定程度上提高了算法的收敛速率。但是，快速迭代收缩阈值算法在解决最小值优化问题时，采用的是固定步长因子，限制了算法的收敛速率。针对该问题，结合Barzilai-Borwein算子提出一种改进的变步长算法。改进算法在每次迭代中利用前两步的迭代信息更新步长因子，加快了算法的收敛。将该算法应用于压缩感知和图像去噪中，数值实验结果表明：该算法改进了原算法的收敛速率。因此,改进变步长快速迭代收缩阈值算法不仅提高了算法的效率，同时提高了信号复原的信噪比。

快速迭代收缩阈值算法；Barzilai-Borwein算子；全变分模型；压缩感知;图像去噪

0 引 言

图像去噪问题[1]是图像复原处理中的一个关键问题。在传感器设备获取图像的过程中，由于传感器缺陷、环境变化以及人为因素等原因，使得图像不可避免地引入噪声。研究图像去噪问题时，一般情况下，针对图像建立去噪模型，然后利用优化理论中逆问题的求解，获取更加容易分析和处理的图像。其中逆问题就是从直接观察到的参数出发，通过迭代计算找到目标函数的一个可行解，使得目标函数值最优。该问题在光学、雷达、声学、通信理论、信号处理、医疗图像、计算机视觉、机器学习[2]、压缩感知[3]等领域均有广泛的应用。

压缩感知(或称压缩采样、稀疏采样)[3]，是一种新的高效获取和恢复信号的信息理论。它突破了香农理论中，当采样频率不低于信号频率的两倍时，就可以无失真地恢复原始信号的理论。压缩感知的核心思想是，若高维信号是可以压缩的或其在某一个变换域中具有稀疏性，则可用一个与变换基不相关的测量矩阵将该信号投影到一个低维空间上，同时这种投影保持了重构信号[4]所需要的信息，然后通过求解一个最优问题，以较高的概率从这些少量的投影中重构出原始信号。其优点是以较少的采样资源，较高的采样速度和较低的软硬件复杂度获得原始信号的测量值。

快速迭代收缩阈值算法(FISTA)[5]是由Beck等提出的一种优化近似分裂算法。该算法将全局加速算子应用于分裂算法，利用函数的前项梯度映射[6]和后项近似映射[7-8]得到问题的近似解。但是在迭代过程中，采用的是固定步长，限制了算法对一般凸优化问题的求解速率。

针对该问题，提出一种变步长的快速迭代收缩阈值算法，并应用于图像的去噪和压缩感知问题中，并进行了实验验证。

1 逆问题及其求解算法

一般问题模型为：

b=Au+n

(1)

其中，A,b,n是已知矩阵，当矩阵A为单位矩阵时，从已知的矩阵b中恢复未知的信号u，则得到如下的逆问题：

(2)

若式(2)中约束项为L1模型，则此时的解是估计压缩信号u的最优解。

故针对文中的压缩感知算例，应用L1正则化模型求解。L1正则化模型为：

(3)

对于图像处理问题，文献[9]提出利用全变分模型(Total Variation,TV)求解图像复原。该模型由Rudin等于1992年提出，用以代替L1模型，可以更好地保存图像的边缘信息。因此针对文中图像去噪算例，应用TV模型进行重构求解[10]。

全变分模型[9,11]定义式如下：

(4)

其中，‖u‖TV表示u关于点i的离散化梯度。因此，当q=2时，‖u‖TV表示各向同性；q=1时，‖u‖TV各向异性。

针对文中算法，选择各向同性，得到图像去噪优化问题的新模型为：

(5)

下面描述一阶优化算法。

对于信号和图像处理等问题中的凸优化求解，通常利用求逆问题，然后选择有效求解的相关算法，如一阶算法[12]。

例如，对于无约束的凸优化问题：

min{f(x):x∈Rn}

(6)

f:Rn→R是具有L-Lipschitiz常数的可微凸函数。即有：

y)∈RN×RN)

(7)

其中，L(f)>0，它是f的Lipschitiz常量。

一般采用梯度下降法[6]最小化f：

算法1：梯度下降算法。

1：Fork=1,2,3…do

2：xk+1=xk-ρf(xk)

End For

min{F(x)=f(x)+g(x):x∈Rn}

(8)

其中，f(x)和g(x)均为凸函数。

此时算法1可以改进为前项后项分裂[13-14]算法(Forward-Backward Splitting,FBS)。

算法2：FBS。

1：Fork=1,2,3…do

2：xk+1=prox(xk-ρf(xk))

End For

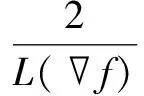
2 快速迭代收缩阈值算法

随着对压缩感知问题研究的兴起，一阶算法的优化问题逐渐成为研究热点。而快速迭代收缩阈值(FISTA)[5]就是一种优化FBS算法。

首先考虑如下问题:

(9)

假设函数g是任意下半连续凸函数，一般情况下，函数g既是不可微的同时函数值趋于无穷大，此时函数g通过计算所谓的近似映射[7-8]的闭合解，同时假设函数f是凸函数，有L-Lipschitz梯度f(见式(7))，则问题的一个近似映射为：

(10)

假设当‖x‖→∞时，f(x)+g(x)→∞。则问题(9)至少有一个解。对于任意的ρ>0，该问题有如下形式的解：

x=proxλg(x-ρf(x))

(11)

该等式有如下迭代的等式：

(12)

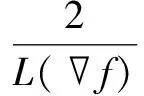
该方法可以分解成首先利用函数f求解前向梯度，然后再利用函数g求解后向近似算子。FISTA算法就是利用映射梯度法和分解法解决变量不等式问题的。当g=0时，式(12)简化为：xn+1=xn-ρnf(x)，即求解一个Lipschitz可微分方程的最小值；当f=0时，式(12)简化为：xn+1=proxρnfxn，即求解一个不可微函数的最小值。因此FISTA算法可以认为是这两种基本方法的组合。

综上所述，FISTA算法可以理解为初始化x0∈RN之后，求解目标函数的前向梯度映射和后向近似映射问题的解：

xn=proxγng(xn-ρnf(xn))

(13)

当0<ρ<2/L(f)，那么该方法收敛到f+g的最小值。

算法3：FISTA。

1：初始化t1=1,y1=x0∈Rn,ρ<2/L(f)

2：Fork=1,2,3…do

3：xk=prox(yk-ρf(yk))

5：yk+1=xk+(xk-xk-1)(tk-1)/tk+1

End For

由于FISTA算法在求解问题中采用的是加速因子，与原始的ISTA[15]算法相比，搜索速度有所增加。

3 改进快速迭代收缩阈值算法

虽然FISTA算法采用了一阶优化的方法，同时采用加速算子，但由于该算法中采用的是固定步长因子的搜索迭代方法，使得算法的搜索速度较慢。基于此问题，在FISTA算法的基础上，采用BB(Barzilai-Borwein)[16]可变步长的快速迭代收缩阈值算法可以加快搜索速度，提高算法的收敛效率。

BB算法的基本思想是利用迭代当前点以及前一点的信息来确定步长因子。在选择临近步长时，用ρnI来模拟Hessian矩阵2f(x)。即迭代的公式为：xn+1=xn-ρngn，可以看作xn+1=xn-Dngn。其中Dn=ρnI。计算ρn，得到min‖sn-1-Dnyn-1‖，其中sn-1=xn-xn-1，yn-1=gn-gn-1。这样做是基于拟牛顿法[17]的提供两点接近切线方程，从而得到迭代方程：

xn+1=xn-ρngn

(14)

(15)

改进算法(称之为FBB算法)描述如下：

算法4：FBB。

1：初始化x0,t0,ρ0=1,u0,φ,k=1

2：xk+1=prox(uk-ρkf(uk))

3：令sk-1=xk-xk-1,yk-1=gk-gk-1,gk=f(xk)

7：uk+1=xk+(tk-1)/(tk+1)(xk-xk-1)

8：更新k=k+1

9：如果满足终止标准，算法停止

4 数值实验

实验测试平台为Window7系统的笔记本，CPU为AMD A6-3400M APU with Radeon(tm) HD Graphics 1.40 GHz 四核，4 GB内存，仿真平台为MATLAB 7.14(R2012a)。

4.1基于L1模型的压缩感知

待恢复信号为5 000个，信号压缩率为5.555 56，分别采用FBB算法和FISTA算法进行信号的恢复。图1是两种算法恢复的效果。

从图中可以看出，两种算法都能达到恢复信号的目的。

目标函数的对比如图2所示。

FBB算法在恢复信号时使得误差更小，更接近信号最优值。信号恢复的信噪比和相对误差如表1所示。在相同迭代步数(150步)时，FBB算法对信号恢复的信噪比更高，效果更优。

图1 压缩感知信号恢复

图2 目标函数对比

表1 图像去噪结果对比

4.2基于TV模型的图像去噪

为了验证文中算法，测试图像为六幅灰度图像，分别为“Cameraman”(256×256)、“Lena”(512×512)、“Plane”(512×512)、“Barbara” (512×512)、“Mandrill”(512×512)、“Peppers(512×512)”。

以“Cameraman”(256×256)为例，测试图像去噪，对图像添加方差为0.01的Gaussian噪声后，采用FBB和FISTA对图像进行去噪实验并作对比分析。

图3为Cameraman去噪图像。

图3 Cameraman去噪图像

相对误差对比如图4所示。

图4 Cameraman图像去噪相对误差对比曲线

从图4可以看出，FBB最终的相对误差值要小于FISTA下的相对误差值，表明图像去噪效果更好。

图5是两算法目标函数随迭代次数的对比及其放大图。从图中可以看出，FBB的目标函数值小于FISTA的目标函数值。

表2是六幅图像都添加高斯噪声后利用两种算法对图像去噪运行时间和去噪前后信噪比对比结果。

表2 图像去噪实验结果对比

图5 Cameraman图像去噪目标函数值对比曲线

从表2可以看出，FBB比FISTA在去噪后图像信噪比较高，同时计算机耗时较短，缩短了近一半的计算时间，提高了图像去噪的速率。

5 结束语

针对传统定步长的快速迭代收缩阈值算法收敛速率慢的问题，提出了一种采用BB可变步长的改进快速迭代收缩阈值算法。该算法在每次迭代之前对步长因子进行更新，加快了算法的收敛速率。数值实验表明：该算法不仅加快了原快速迭代收缩阈值算法的效率，而且提高了恢复图像的质量。

[1] 刘 文,吴传生,许 田.自适应全变分图像去噪模型及其快速求解[J].计算机应用研究,2011,28(12):4797-4800.

[2] 郭亚宁,冯莎莎.机器学习理论研究[J].中国科技信息,2010(14):208-209.

[3] 戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011,34(3):425-434.

[4] 谢志鹏.基于前向后向算子分裂的稀疏信号重构[J].南京大学学报:自然科学版,2012,48(4):475-481.

[5] Beck A,Teboulle M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202.

[6] Chen X, Lin Q, Kim S, et al.Smoothing proximal gradient method for general structured sparse regression[J].Annals of Applied Statistics,2012,6(2):719-752.

[7] Parikh N,Boyd S.Proximal algorithms[J].Foundations and Trends in Optimization,2013,1(3):123-231.

[8] Combettes P L,Pesquet J C.Proximal splitting methods in signal processing[M]//Fixed-point algorithms for inverse problems in science and engineering.New York:Springer,2011:185-212.

[9] Rudin L I,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1-4):259-268.

[10] 李艳红.基于全变分模型压缩传感图像重构的快速算法[D].郑州：河南大学,2012.

[11] 余丽红,冯衍秋,陈武凡.基于自适应正则化的全变分去噪算法[J].中国图象图形学报,2009,14(10):1950-1954.

[12] Jensen T L.First-order convex optimization methods for signal and image processing[D].Denmark:Aalborg University,2011.

[13] Tseng P.Applications of a splitting algorithm to decomposition in convex programming and variational inequalities[J].SIAM Journal on Control and Optimization,1991,29(1):119-138.

[14] Combettes P L,Wajs V R.Signal recovery by proximal forward-backward splitting[J].SIAM Journal on Multiscale Modeling & Simulation,2005,4(4):1168-1200.

[15] Bioucas-Dias J M,Figueiredo M A T.A new TwIST:two-step iterative shrinkage/thresholding algorithms for image restoration[J].IEEE Transactions on Image Processing,2007,16(12):2992-3004.

[16] Barzilai J,Borwein J M.Two-point step size gradient methods[J].IMA Journal of Numerical Analysis,1988,8(1):141-148.

[17] 桂胜华,周 岩.拉格朗日-拟牛顿法解约束非线性规划问题[J].同济大学学报:自然科学版,2007,35(4):556-561.

AnImprovedFastIterativeShrinkage-thresholdingAlgorithmwithVariableStepsize

CHEN Shao-li，YANG Min

(College of Automation，Nanjing University of Posts and Telecommunications，Nanjing 210023，China)

Image restoration is an important research in image processing and solving of it involves large databases and many unknowns.The forward-backward splitting method provides a simple,practicable solution to solve the kinds of data optimization with high dimension.The fast iterative shrinkage-thresholding algorithm joins the global acceleration operator and improve its convergence rate based on the forward-backward algorithm.However,the fixed step-size limits its speed of the convergence in minimal optimization solving.To address that,an improved algorithm with variable stepsize by using Barzilai-Borwein (BB) operator is proposed which updates the step size with the iterative information of the first two steps in each iteration to accelerate its convergence.Then it’s applied to image denosing and compressed sensing.The experimental results demonstrate that it is more efficient than the original fast iterative shrinkage-threshold algorithm,not only in the efficiency but also in the signal to noise ratio of signal restoration.

fast iterative shrinkage-threshold algorithm;Barzilai-Borwein operator;total variation model;compressed sensing;image denosing

TP391

A

1673-629X(2017)10-0069-05

2016-08-10

2016-11-16 < class="emphasis_bold">网络出版时间

时间：2017-07-19

国家自然科学基金资助项目(61271234)

陈少利(1990-)，女，硕士，研究方向为基于全变分模型的图像复原算法；杨 敏，博士，副教授，研究方向为计算机视觉与图像理解。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170719.1108.008.html

10.3969/j.issn.1673-629X.2017.10.015