覆盖粗糙集算子的性质及关系之注记

夏秀云，常安成，刘一龙

(湖南信息学院 公共课部，长沙 410005)

覆盖粗糙集算子的性质及关系之注记

夏秀云，常安成，刘一龙

(湖南信息学院 公共课部，长沙 410005)

覆盖粗糙集是粗糙集的一种推广，也是为了刻画信息系统中具备不完备性与模糊性的信息. 本文借助邻域，首先定义了几对覆盖粗糙集算子，然后根据定义研究了这几对覆盖粗糙上、下近似算子的性质及定理，并讨论这几对覆盖粗糙集算子的相关性，最后还讨论了这几对上、下近似算子对偶的等价条件.

粗糙集；覆盖；近似算子

经典粗糙集理论是1982年波兰数学家Pawlak首次提出来的，它是集合理论的一种推广[1].粗糙集理论是用来处理模糊和不确定性的知识，已经广泛用于人工智能、模式识别、过程控制、数据库的知识发现和专家系统等方面[2-11]. 其中属性约简是粗糙集理论的一个很重要应用部分，所以对其进行研究是很有意义的工作. 经典粗糙集的属性约简只是通过划分或者等价关系来约简条件属性，这严重局限了粗糙集理论的发展.基于上述原因，故有学者把划分扩展到覆盖，使得粗糙集理论研究的范围大大地扩展了[9]. Z.Bonikowsk从实际应用出发，提出了覆盖粗糙集模型，讨论了相关的性质[5].之后，Mordeson等从另外的角度对覆盖近似集进行了研究，给出了基于覆盖的近似集的相互关系和公理化体系[6]，使得从逻辑和代数上搞清楚了覆盖上、下近似运算的结构和本质.紧接着，陈德刚等从格的角度出发，提出了完备分配格的覆盖粗糙集模型[11].针对Z.Bonikowski定义的算子不具有对偶性，特别是其上近似算子不满足单调性.许多学者对其定义的近似算子做了适当的修改.其中，William Zhu提出了几种新的覆盖上近似算子，并讨论了它们的性质、公理化条件及其相互关系.本文笔者首先给出了几对新的覆盖上、下近似算子，讨论他们各自的性质及定理，并且研究这几对算子彼此之间的关联性，最后还给出了这对近似算子对偶的等价条件，这对覆盖粗糙集模型的深入研究起到一定参考作用.

1 预备知识

定义1[2]设U是一个论域，A是U的子集族，如果A中所有子集非空，并且∪A=U，则称A是U的一个覆盖.显然，U的一个划分也是一个覆盖，覆盖是划分的推广.

定义2[2]设(U，A)为一个覆盖近似空间，∀x∈U，称md(x)={K∈A;x∈K∧∀S∈A(x∈S∧S⊆K→K=S)}，为x关于(U,A)的最小描述.

定义3[10]设(U,A)是一个覆盖近似空间，x∈U，称N(x)=∩cv(x)=∩{K∈A;x∈K}为x的邻域，其中cv(x)={K∈A;x∈K}.注意到md(x)是cv(x)中关于包含关系的极小元构成的集合，故N(x)=∩md(x).

定义4 设(U,A)是一个覆盖近似空间,X⊆U,则可得到如下几对覆盖粗糙上、下近似算子：

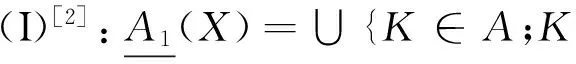
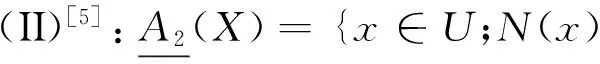
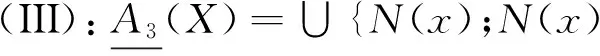
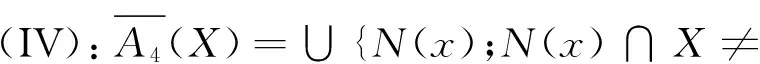
2 覆盖粗糙算子的性质

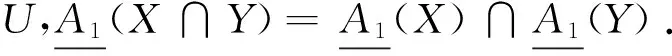
定理1 设(U,A)为一个覆盖近似空间, 对于任意X,Y⊆U, 则有以下性质成立：

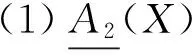
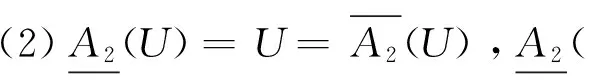
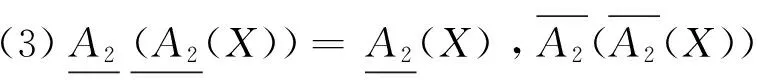
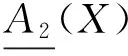
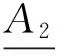
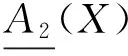
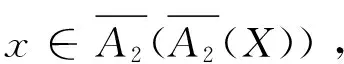
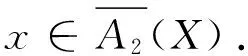
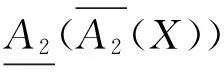
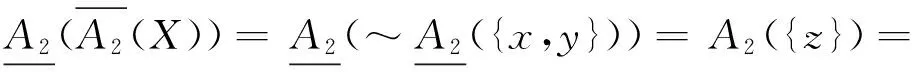
定理2 设(U,A)为一个覆盖近似空间, 对于任意X,Y⊆U, 则

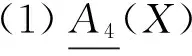
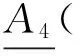
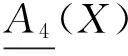
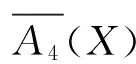
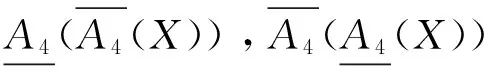
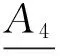
证明 由算子(II)的定义知，易证(1)，(2)，(3)，(5). 以下我们只证明(4)式.

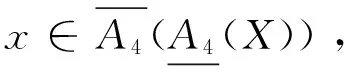
定理3 设(U,A)为一个覆盖近似空间, 对于任意X,Y⊆U, 则

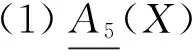
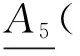
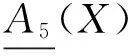
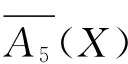
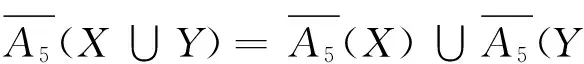
证明 根据覆盖算子(V)的定义可得.该定理的证明过程类似例1及定理2.

3 覆盖粗糙算子的相关性

定理4 设(U,A)为一个覆盖近似空间,A0=U,则算子(I)与算子(II)等价.

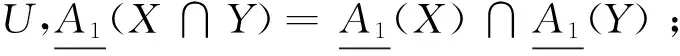
定理5 设(U,A)为一个覆盖近似空间, 对任意X⊆U,则

证明 (1)设

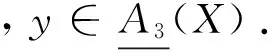
定理6 设(U,A)为一个覆盖近似空间, 若对于任意X⊆U, 则

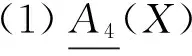
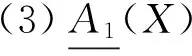
推论1 设(U,A)为一覆盖近似空间, 若对于任意X⊆U, 则

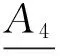
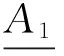
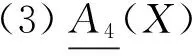
证明 证明类似于定理4，这里不再累述.

引理1 设(U,A)为一覆盖近似空间, {N(x);x∈U}的形成U的划分充分必要条件对于任意x,y∈U,x∈N(y),则y∈N(x).

证明 因为x∈N(y)且x∈N(x),则x∈N(y)∩N(x)，又因{N(x);x∈U}⊂U且N(y)∩N(x)=∅，N(x)≠N(y),因此N(y)=N(x).又因y∈N(y),从而y∈N(x).另一方面，假设存在N(y)∩N(x)=∅，N(x)≠N(y)对于任意x∈N(y)且y∈N(x)，则存在z∈N(y)∩N(x), 故z∈N(x),又因x∈N(z)且x∈N(x),则x∈N(z)∩N(x),从而N(z)=N(x).又因z∈N(y)且y∈N(z),y∈N(y),则y∈N(y)∩N(x)，因此N(y)=N(x),即{N(x);x∈U}形成U的划分.

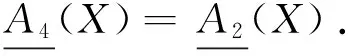
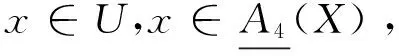
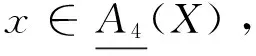
推论2 设(U,A)为一个覆盖近似空间,则以下条件相互等价:

(1){N(x);x∈U}形成U的一划分；

(2)算子(II)⟺ 算子(IV);

(3)算子(II)⟺ 算子(V);

(4)算子(IV)⟺ 算子(V).

证明由推论1可得，(2)式和(3)式成立，故可得(4)式成立.又由定理7可得，(1)⟺(2)中算子(II)的下近似=算子(IV)的下近似；同理可证，(1)⟺(2)中算子(II)的上近似=算子(IV)的上近似，从而(1)⟺(2).故有(1)⟺(2)⟺(3)⟺(4).证毕.

4 结 论

某一论域上的等价关系与该论域的划分互相确定,划分是一种特殊的覆盖.本文研究了几对覆盖上、下近似算子的性质及定理，讨论这几对覆盖算子的关联性，另外给出了上、下近似算子对偶的等价条件.基于以上研究，这对覆盖粗糙集模型的进一步研究起到一定的参考意义.

[1] Z.Pawlak,Rough sets.International Journal of Computer and Information Sciences[J].1982,11(82):341-356.

[2] Zbigniew Bonikowski,Edward Bryniarski,Urszula Wybraniec-Skardowska, Extensions and Intentions in the Rough Set Theory[J].Information Sciences,1998,107(98):149-167.

[3] G.Cattaneo,Abstract Approximate Spaces for Rough Theories[M].in:Polkowski,Skowron (Eds.),Rough Sets in Knowledge Discovery 1:Methodology and Applications,Physicaverlag, Heidelberg,1998,59-98.

[4] H.S.Nguyen,D.Slezak,Approximation Reducts and Association Rules Correspondence and Complexityresults[J].in:N.Zhong,A.Skowron,S.Oshuga(Eds.),ProceedingsofRSFDGrC’99,Yama Guchi,Japan,LNAI 1999.1777(234):137-145.

[5] Z.Bonikowski,E.Bryniarski,U.Wybraniec.Extensions and Intensions in the Roughset Theory[J].Joural of Information Sciences,1998, 107(46):149-167.

[6] J.N.Mordeson.Rough Set Theory Applied to (fuzzy) Ideal Theory[J].Joural of FuzzySets and Systems, 2001,121(78):315-324.

[7] Z.Pawlak,Andrezej Skowron, Rough Sets:Some Extensions[J].Information Sciences,2006,17(26):28-40.

[8] Chen Degang,Wang Changzhong,HuQinghua,A New Approach to Attribute Reduction of Con-sistent and Inconsistent Covering Decision Systems with Covering Rough Sets[J].Information Sciences,2007,177(49):3500-3518.

[9] E.Bryniarski,A Calculus of Rough Sets of the First Order[J]. Bulletion of the Polish Academy of Sciences,1989,16(20):71-77.

[10] 高 岩,秦克云.基于覆盖的粗糙近似算子[J].计算机工程与应用,2007,43(21):75-78.

[11] Chen Degang,Zhang Wenxiu,S.Yeung,C.C.Tsang,Rough Approximations on a Completely Distributively Lattice with Applications to Generalized Rough Sets[J]. Information Sciences,2006, 176(57):1829-1848.

StudyonDegradationofPesticideResiduesinVegetablesandFruitsByOzone

XIA Xiu-yun，CHANG An-cheng，LIU Yi-long

(Department of Public Course,Hunan Institute of Information Technology, Changsha 410005, China)

The covering rough sets theory is a generalization of traditional rough set theory,and also describes the information with incompleteness and fuzziness in information system. Firstly, we define several operators on covering rough sets by epsilon neighborhood. Secondly, we discuss properties, theorems and relations of those operators. Finally, we also get conditions of equivalence with dual of those operators.

rough sets; covering; approximation operators

0159

A

1671-119X(2017)03-0043-04

2017-03-29

国家自然科学基金项目(60474022)；湖南省教育厅科研资助项目(16C1118).

夏秀云(1980-)，女，硕士，讲师，研究方向：智能信息处理.