例析数学题中的巧设“堑”
谢 昌
(江西省赣州市第七中学,江西 赣州 341000)
例析数学题中的巧设“堑”
谢 昌
(江西省赣州市第七中学,江西 赣州 341000)
本文笔者根据多年从教初中数学解题教学的实践经验,在命题训练中巧妙设堑,故意让学生掉进堑里,以唤醒学生学习的有意注意,从而弥补学生知识学习的盲点.这在数学解题教学中将会收到良好的教学效果.
例析;数学题;设堑
常言道 “吃一堑长一智”,说的是人们经受过挫折后获得的胜利感到格外的欣慰和开心,对成功的经验倍加珍惜.同样,在我们的数学教学过程中,教师也可抓住这一心理现象.在训练题中巧设堑,让同学们在“上当”中醒悟,将会收到良好的数学教学效果.如何设好堑?笔者认为从以下几个方面来设堑.
1.利用忽视零及零的特性来设
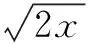
A.-2 C.-1≤m≤2 D.-1 由已知条件可知判别式值大于零,但一元二次方程的一般式中二次项系数不应为零,这是造成错解的普遍原因. 2.利用漏解来设 例2 相交两圆的公共弦长为24,两圆的半径分别是15与20,那两圆的圆心距等于( ) A.9 B.7 C.25 D.7或25 两圆相交有两种情况,即圆心在公共弦的同旁和两旁,本题无图形,故极易忽视同旁这种情形而选不到D. 3.利用符号问题(尤其是负号)来设 此题理解不到一个隐含条件m<0,式子的值应负数,而难以选到C. 4.利用容易混淆的概念、法则来设 例4 若x=1a=-b≠0,n是自然数,则下面结论正确的是( ) A.a2n和b2n互为相反数 B.an和bn互为相反数 C.an+1和bn+1互为相反数 D.a2n+1和b2n+1互为相反数 a与b互为相反数,由乘方法则则可知只有当同次奇次方时,其幂也为相反数,知道了这点就不会上当. 5.利用审题粗心来设 例5 用换元法解方程(x2-2x-1)(x2-2x+2)=10,下列的换元中,不适宜的是( ) A.x2=yB.x2-2x=y C.x2-2x-1=yD.x2-2x+2=y 此题中的“不”字害死不少粗心的学生.一反常态的命题偶尔出现考你细心不细心. 6.利用多解或取值范围扩大来设 A.x≠4,x≠3 B.x≠4,x≠-3、 分母不能为零,除式不能为零,必须牢牢把握住,否则很难选到C. 上述选例虽属浅显,却击中了不少同学的要害, 同时也给我们反馈了极为宝贵的信息,从而为变换我们的教学方法和策略提供了依据,变强攻为智取,以达到教得轻松,学得愉快,师生共赢之目的. [1]王洪军.学生数学学习中易错点的成因及应对策略[J].语数外学习(初中生版)下旬,2014(5). G632 A 1008-0333(2017)23-0008-01 2017-07-01 谢昌(1981.9-),男,江西省赣州市人,本科学历,中学一级教师,主要研究方向为初中数学教育教学. [责任编辑李克柏]
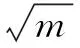


——赣州市审计局这样让困难群众感受温暖

