两点间距离公式在中考难题中的应用

薛 丹

(常州市清潭中学，江苏 常州 215000)

两点间距离公式在中考难题中的应用

薛 丹

(常州市清潭中学，江苏 常州 215000)

常州中考是“毕业考试”与“升学考试”两卷合一，这就要求在命题上兼顾“水平测试”与“选拔性考试”的双重功能，在这大背景下，中考能力题难度加大大势所趋，这就更需要学生对初中数学知识能综合灵活运用，但某些难题如果借助高中数学知识可以轻易解决．因此，教师在日常教学中可以适当介绍一些利用初中数学知识可推导得出的高中数学公式，譬如本文所涉及到的平面直角坐标系中两点间距离公式．

中考；两点间距离公式；应用

一、预备知识

1.若两点都在x轴上，且已知A(x1，0)，B(x2，0)时，有|AB|=|x2-x1|，即AB2=(x2-x1)2．

2.若两点都在y轴上，且已知A(0,y1)，B(0,y2)时，有|AB|=|y2-y1|，即AB2=(y2-y1)2．

3.若已知两点坐标为A(x1,y1)，B(x2,y2)．作点A关于x轴的垂线，再作点B关于y轴的垂线，两条垂线交于C点．如右图：

显然∠C=90°，这样我们就构造出了一个直角三角形ABC，而我们要求的AB就是这个直角三角形的斜边.由题意得C(x1,y2)，则AC2=(y2-y1)2，BC2=(x2-x1)2.

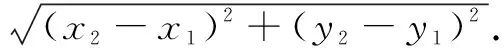
即两点间的距离等于这两点的横坐标之差的平方与这两点的纵坐标之差的平方和的算术平方根．

引例(1)已知A(3，0)，B(0，4)，求AB；(2)已知C(2，1)，D(-1，-1)，求CD.

解(1)AB2=(3-0)2+(0-4)2=25，则AB=5.

二、两点间距离公式在中考难题中的应用

1.数量关系

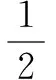
解由题意得：点A(2，0)，点B(0，1)，

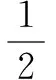
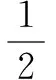
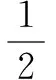
2.最值问题

例2 (2014年常州市中考模拟第17题)已知点A(0，-4)、B(1，0)、C(a，-a)，若过点C的圆的圆心是线段AB的中点，则这个圆的半径的最小值等于________．

解∵点A(0，-4)，B(1，0)，

∵点C(a，-a)在⊙O上，

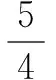
3.等腰三角形

②若AB=BC，则AB2=BC2，即

4.直角三角形

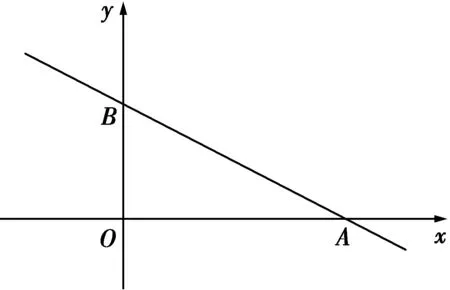
例4 (2016年常州市一模第27题)如图，已知直线y=x+b(b>0)与x、y轴分别交于A、B两点，点C(1，0)，过点C作垂直于x轴的直线l．在直线l上取一点P，满足PA=PB．点A关于直线l的对称点为点D，以D为圆心，DP为半径作圆D．试说明：直线BP与圆D相切．

解由题意得：B(0,b)，D(2+b,0)，P(1,-1).

则BD2=(2+b)2+b2，PB2=12+(b+1)2，PD2=(b+1)2+12.

易得BD2=PB2+PD2，则DP⊥BP.

又∵BP经过圆D半径外端，

∴直线BP与圆D相切.

综上所述，如果在平面直角坐标系中线段两端端点可用未知元素表示，则我们可以利用两点间距离公式将其所对应的线段长表示出来，线段长可表示即可寻找等量关系构造方程进行求解，从而将未知元素求出．而如果纯粹使用初中数学知识对类似问题加以解决的话，需要学生具有较强的识图能力，能对初中数学知识加以综合运用，这样的要求对绝大多数考生而言略高．所以教师在中考总复习中还应适当补充学生能理解能使用的简单高中数学公式．

[1]李朝东.2013年江苏十三大市中考试卷汇编[M].宁夏:宁夏人民教育出版社，2013.

G632

A

1008-0333(2017)23-0005-02

2017-07-01

薛丹(1980.12-)，男，江苏常州人，中学一级教师，大学本科，主要研究中考解题技巧.

[责任编辑李克柏]