不同浪向下导管架下水过程的动力学分析

张大朋，白 勇，朱克强，刘 建，桂琴琴

1.浙江大学建工学院，浙江杭州 310058

2.宁波大学海运学院，浙江宁波 315211

不同浪向下导管架下水过程的动力学分析

张大朋1，白 勇1，朱克强2，刘 建2，桂琴琴2

1.浙江大学建工学院，浙江杭州 310058

2.宁波大学海运学院，浙江宁波 315211

导管架下水过程较为复杂，操作不慎会有可能发生触底现象。为提高施工的安全性和可靠性，需要对导管架的下水过程进行分析。基于凝集质量法，将导管架离散成凝集质量模型，参照管架结构具体参数，结合导管架下水的具体过程，通过必要的简化，利用动力学分析软件OrcaFlex建立了不同浪向下导管架下水过程的动力学模型，发现浪向的变化对导管架下水过程有着非常明显的影响：不同浪向下，导管架脱离驳船甲板滑入海水中的时刻不尽相同，且与甲板的接触力也不尽相同；浪向的改变对导管架质心轨迹在水平面内的影响较大，而在竖直高度上导管架质心的位置变化随着浪向的改变在时域上会有所不同，但其质心高度位置图像整体呈现一定的相似性，等。计算结果对研究导管架下水有一定的指导意义，可为研究导管架下水提供技术支持。

凝集质量法；OrcaFlex；导管架下水；动力学分析

一般而言，导管架平台的体积都比较庞大，其质量从一两千到几万吨不等。如此巨大的结构物，在其沿着驳船轨道纵向滑入水中时，如操作不慎，极有可能发生触底现象，使导管架受到猛烈的碰撞和冲击，从而导致安全事故的发生。为了使工程的安全性及可靠性得到充分的保证，需要对导管架的下水过程进行参数计算和模拟分析，得出其运动轨迹、参数以及系统的受力情况等，以便为实际下水过程提供参照。

在八十年代以前，国内外对导管架下水的研究仅仅局限于二维空间[1-2]。随着计算机仿真技术的发展，八十年代末到九十年代中期，对导管架下水过程的研究由二维扩展到三维空间。上海交通大学的刘应中等对导管架的三维下水过程进行了理论推导和实验对比[3-4]；1999年前后，美国开发出海工软件SACS，该软件可对导管架下水过程进行三维仿真，但该软件中没有考虑风浪流对系统的作用及风和浪对导管架的作用；2003年，国内中海油的杨晓刚运用MOSES软件对导管架下水过程进行了仿真，但没有考虑风浪流的作用。中海油的蔡元浪等运用MOSES和SACS结合的方法对导管架下水过程中波浪、水深、风速等参数的敏感性进行了分析。波浪作为一个很重要的参数，对于导管架下水过程有着十分重要的影响，因此在导管架下水过程中应该对其进行考虑。

不管是用SACS还是MOSES对导管架下水过程进行动态分析，其建模过程都较为繁琐，导管架初始运动设置较为复杂，且随着外界环境载荷的加剧使得收敛难度大为增加。因此需要一种相对简便易于收敛的建模方式。本文基于凝集质量参数法对导管架进行了离散，结合大型水动力软件OrcaFlex运用时域耦合动力学分析法建立了导管架下水过程的动力学分析模型，对不同浪向下导管架下水的轨迹进行了特性研究。结合动力学仿真的结果给出了一些指导性建议，对具体工程实践有一定的指导作用。

1 海洋环境载荷的计算理论

1.1 波浪理论的选择

OrcaFlex能依据不同的水深、波浪周期及波高来确定规则波列，在OrcaFlex中不同波列对应的不同的波浪理论有着明确的规定。引入一个与波高、波长及水深相关的系数U：

式中：H为波高；L为波长；d为水深。

如果U＜40，说明波浪较小，适用斯托克斯五阶波理论；若U＞40，则是定常波，宜用椭圆余弦波理论。需要注意的是，理论上而言，流函数公式对于任何波都适用，如果选择了别的理论，应将其计算结果与流函数理论的计算结果相比较以确保其有效性。数值40并不是一个精确的固定标准，当U值接近40时，使用斯托克斯第五理论或余弦波理论都不能保证计算的准确性，在这种情况下，OrcaFlex推荐使用流函数法，如果与40相差较大，那么相关的分析理论（如斯托克斯第五或余弦波理论）将会得到很好的应用。总之，在大多数例子中，OrcaFlex推荐使用流函数法。为了保证计算的准确性，本文选择流函数法（stream function order取为5）。

1.2 船体波浪响应幅值算子

通过波浪的响应幅值算子（Response Amplitude Operator，以下简称RAO）可以得到船体在波浪中的运动行为。海洋平台及驳船的RAO一般可以通过船舶的水池模型实验来获得。其本质是一个波浪传递函数，在OrcaFlex中，一旦海洋平台/驳船的RAO确定，那么波浪所引的起平台/驳船的运动就可以确定。

驳船在波浪作用下的运动响应特性可以用RAO进行描述。一阶波浪力所引起的船体偏移用波浪响应幅值算子进行定义，有：

式中：x是浮体位移响应（升沉、纵荡、横荡是长度单位，艏摇、横摇、纵摇是角度单位）；a、ω分别是波浪的振幅、频率；R是RAO响应的系数；φ是相位；RAO的坐标原点取在船体的设计水线处。

1.3 导管架与驳船接触力及摩擦力的计算

对于两物体之间法向接触力的计算，国内外相关的应用成果基本上采用的是动能公式的形式[13]，但在OrcaFlex中却并不是这样算。在OrcaFlex中，船体本身是一个无法变形的刚体。要计算船舶的法向接触力，需要在船体表面加一层弹塑性固体，进而建立导管架与驳船的弹性变形动力分析模型，根据弹塑性固体的变形量计算出船舶甲板与导管架的法向接触力Fp（kN）为：

式中：K为弹塑性材料的法向材料刚度，kN/（m·m2）；Ap为面面接触时的正对时接触面积，m2；d为发生面面接触时在垂直弹塑性固体表面方向的变形深度（也叫法向穿透深度），m。在本算例中材料的法向材料刚度取为10 000 kN/（m·m2）。需要指出的是，在静止时，导管架与驳船上的弹塑性固体之间的法向接触力数值就是导管架自重。

对于摩擦力的计算则是运用优化的库伦模型来算出导管架在下水过程中与驳船之间摩擦力的大小。其计算原理为假设因摩擦引起的变形会导致弹塑性固体变形并产生一个沿摩擦力方向的变形量，随着这个变形量的增大，摩擦力会呈现先线性增大后不变的趋势。单位长度摩擦力F（kN/m）的具体表达式为：

式中：Ks为弹塑性材料的切向刚度，kN/（m·m2）；A为面面接触时的正对时的滑动摩擦接触面积，m2。需要指出的是，只有在动态分析时才考虑OrcaFlex中弹塑性固体的法向接触力和摩擦力。

1.4 导管架波浪力的计算

导管架主要由大量中空挠性圆柱体组成。对于导管架这类小尺度挠性结构物可忽略结构对波浪的影响。波浪对于导管架的作用力可以分为两部分，即拖曳力FD和惯性力FI。波浪力F通常用Morison公式进行计算。1974年Berge和Penzien提出适应结构具有弹性变形产生的位移时的Morison方程修正式，如果垂直圆柱体在波浪中自由摇摆，在莫里森方程中必须使用相对速度和相对加速度，方程必须扩展为：

式中：CD和CM分别代表拖曳力系数和惯性力系数，ρ为海水密度，D为圆柱体直径，u为水质点运动速度，v为圆柱体运动速度。这两个系数的取值与Reynolds（Re）数值和Keullegan-Carpenter（KC）数值有关，这已被研究人员在实验上证实。莫里森方程显示，波浪力由拖曳力和惯性力组成，惯性力与水质点加速度成比例，拖曳力组成与波粒子速度平方成比例。

而在OrcaFlex中对波浪力的计算正是基于修正后的Morison公式。

1.5 导管架杆件结构张力的计算

导管架的杆件结构张力可运用凝集质量法进行计算，可参考文献[8-13]，本处不再赘述。

2 在OrcaFlex中导管架下水模型的建立

2.1 驳船模型的建立

依据驳船具体型宽（16 m）、型深（13.32 m）、船长（103 m）、排水量（8 800 t）、吃水（6.66 m）、设计水线面以上正面投影（191 m2）、设计水线面以上侧面投影（927 m2）、方形系数CB（0.804）、首摇转动惯量（5.83×106kg·m2）、横稳性半径（1.84 m）、纵稳性半径（114 m）及具体RAO等数据应用软件建立船体模型。本文的驳船RAO及波浪漂移QTFs的数据依据实船在某实验水池的衍射分析而来。因驳船本身在软件中被视作刚体，无法计算导管架在下水过程中与船体的摩擦与碰撞。因此在驳船的表面加一层弹塑性固体来实现导管架下水时与驳船甲板的接触与滑动摩擦。导管架下水示意见图1，图中的A、B、C、D均由弹塑性固体组成，由A、B、C、D组成了滑道及滑道侧壁，为保证导管架能顺利滑下，船有2.2°的纵倾角。

2.2 导管架模型的建立及模型中下水的实现

导管架及相关环境相关参数：质量850 t，转动惯量1499 618 181.8kg·m2，重心至滑道高度8.25 m，导管架杆件数为136件；本模型水深为100 m，波高为2 m，每隔15°取一个浪向，波浪周期为5 s。

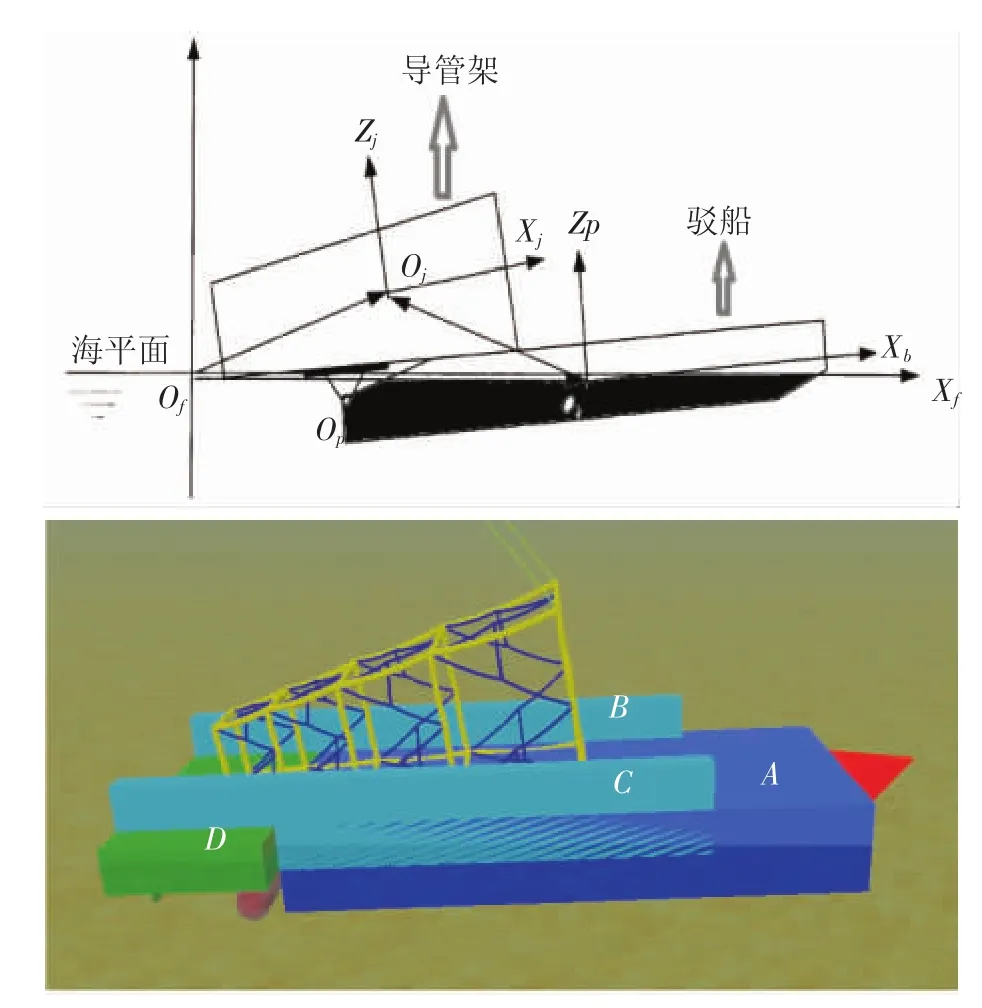
图1 导管架下水模型示意

在建模时，为了使导管架在驳船上沿轨道滑下，需要给导管架一个沿导轨向下的初速度，以便其能顺利沿着滑道滑下。在OrcaFlex中通过运用Link模块（该模块具有弹簧阻尼器的功能）实现此功能。在建模的初始时刻通过设置相关参数，给予Link模块一个压缩刚度（本模型中设力为1 000 kN及一个未被拉伸时的长度）。在本模型中用到了3个Link，分别命名为Link1、Link2、Link3，其在模型中的具体布放位置如图2所示。

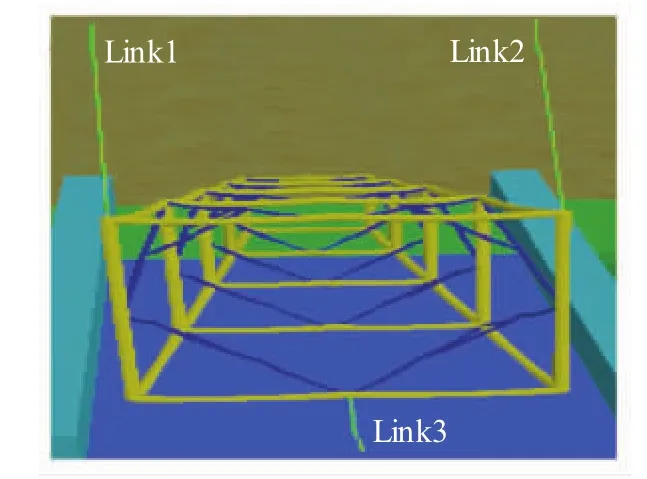
图2 L ink布放位置示意

未被拉伸时的原长分别设为25、25、10 m，在静平衡阶段通过改变Link与导管架和船体相连的两端的空间坐标位置使Link均处于被拉伸的状态，由于驳船有一定的尾倾，在3个Link的拉伸作用下，导管架自重沿滑道向斜下的分量被3个Link提供的拉力平衡，此时导管架处于静止状态；当静平衡结束的瞬间，3个Link立即将导管架释放，此时导管架自重沿驳船滑道斜向下的分量无法被平衡，因此导管架就开始沿着滑道向下滑动，最终滑入海水中。而对于导管架在下水过程中的摇臂则用一个弯曲刚度及扭转刚度很大的缆模块结合Link模块和6D浮标进行组合，具体如图3所示。

图3 摇臂布置示意

3 计算结果

根据设定的主算参数得到外接载荷条件下的数值仿真结果，并对不同浪向下导管架下水过程进行分析。仿真时间共77 s，其中静平衡阶段5 s，动态分析阶段72 s。由于导管架在30 s以内已经从拖船上滑入水中并且数据点非常繁多，如果在整个时域上进行采点，则绘出的数据图像不利于导管架下水规律的总结，因此在对导管架与滑道及滑道侧壁的接触力数据的处理过程中，在时间上取到30 s。而对于导管架自身的动态分析数据如导管架的速度与加速度、导管架的角速度、导管架的轨迹则取整个时域上的数据值进行处理。

3.1 不同浪向下滑道及滑道侧壁对导管架的支持力

不同浪向（设波浪沿着船首方向为0°，沿着船艉方向为180°）下滑道及滑道侧壁对导管架的支持力见图4。

观察图4可发现：在不同浪向时甲板对导管架的垂直支持力在数值的大小和时域上的分布上各不相同。

（1）当浪向为105°时，在仿真达到静平衡后其甲板垂直接触力在动态仿真阶段迅速降为0，在仿真中发现在这一浪向下在达到静平衡后导管架迅速从滑道侧壁一侧横滚入海中，在导管架与滑道侧壁一侧的接触过程中通过与滑道侧壁的相互作用对甲板底部传递一个垂直向上的力的作用，而在软件的计算原理中，支持力的计算是通过贯穿深度的变化计算的，但在这种情形下，相当于贯穿深度是负的，这也正是造成了在计算结果中105°浪向时在静平衡状态甲板对导管架的支持力的计算结果在图中显示是负值的原因，这也说明在浪向为105°时导管架不会沿着滑道滑入海水中，而是会与两个侧壁发生急剧的碰撞挤压及摩擦，进而横滚入海，这是一种极其危险的情况，因此应避免在这种浪向下施工。

图4 不同浪向下滑道及滑道侧壁对导管架的支持力

（2）除105°浪向外，不同浪向时甲板支持力变为0的时刻在时域上是不同的，这说明，不同浪向下，导管架脱离甲板滑入海水中的时刻也不尽相同，不同浪向时的脱离时刻按照先后顺序排列依次为165°、0°、180°、30°、15°、45°、150°、135°、120°、60°、75°、90°，也就是说，165°浪向时导管架最先脱离支撑甲板，90°横向浪向时导管架最晚脱离支撑甲板。

（3）对比观察发现，导管架下水所用时间越久，甲板支撑力曲线变化越和缓且甲板支撑力最大值越小，分析产生这种现象的原因为：下水时间越短，甲板与导管架直接的接触与摩擦越剧烈，从而使得导管架对甲板的冲击越大。对比观察滑道左侧壁与右侧壁与导管架之间的支撑力图像发现：大部分浪向下导管架与右侧壁的接触力为0（0°与15°除外）；而观察滑道左侧壁的支撑力的值发现，在15°、30°、150°、165°时左侧壁的支撑力为负值，依据接支撑力的计算原理，此时的导管架对左侧壁的贯穿深度是负值，也就是说此时的导管架除了会沿着滑道方向下滑外还会相对于支撑甲板向右侧壁滑动，从而通过支撑甲板给予左侧壁底端一个向右拉伸的力，进而导致仿真结果计算出的左侧导管架在这些浪向下的接触力是负值；在浪向为135°和60°时左侧壁对导管架的支撑力为正值，这说明这时导管架会与左侧壁发生接触碰撞，在0°和15°时导管架会与右侧壁发生碰撞；也就是说，在浪向为45°、75°、90°、120°、180°时，导管架与滑道左侧壁和右侧壁均无任何形式的接触力的作用，如在这些浪向下进行导管架下水作业，可以避免或减少导管架与滑道侧壁的碰撞。

3.2 不同浪向下导管架的轨迹

不同浪向下导管架质心在水平面内的运动轨迹见图5。

观察图5可发现：

（1）在0°和180°浪向时导管架质心在XY平面内的偏移并不大，保持Y坐标不变的情况下的近似直线运动，其质心大体在-45 m＜X＜20 m，Y=-10 m的区域内运动；而在浪向为45°、15°、30°时其在水平面内的轨迹呈现一定的相似性，总体呈现随着X坐标的增大，Y坐标值先增大后减小的运动，其质心大体在-45 m＜X＜20 m，-5 m＜Y＜20 m的区域内运动，其轨迹近似呈一个不规则的倒抛物线形态；当浪向为60°、75°、90°、120°、135°时，导管架质心在水平面的轨迹大体相同，呈现出一种近似对数函数的形态，即X坐标均大于0，Y坐标随着X坐标的增大先迅速减小，其图像逐渐趋向于平行于X轴，其质心大体在25 m＜X＜65 m，-75 m＜Y＜-5 m的区域内运动；。

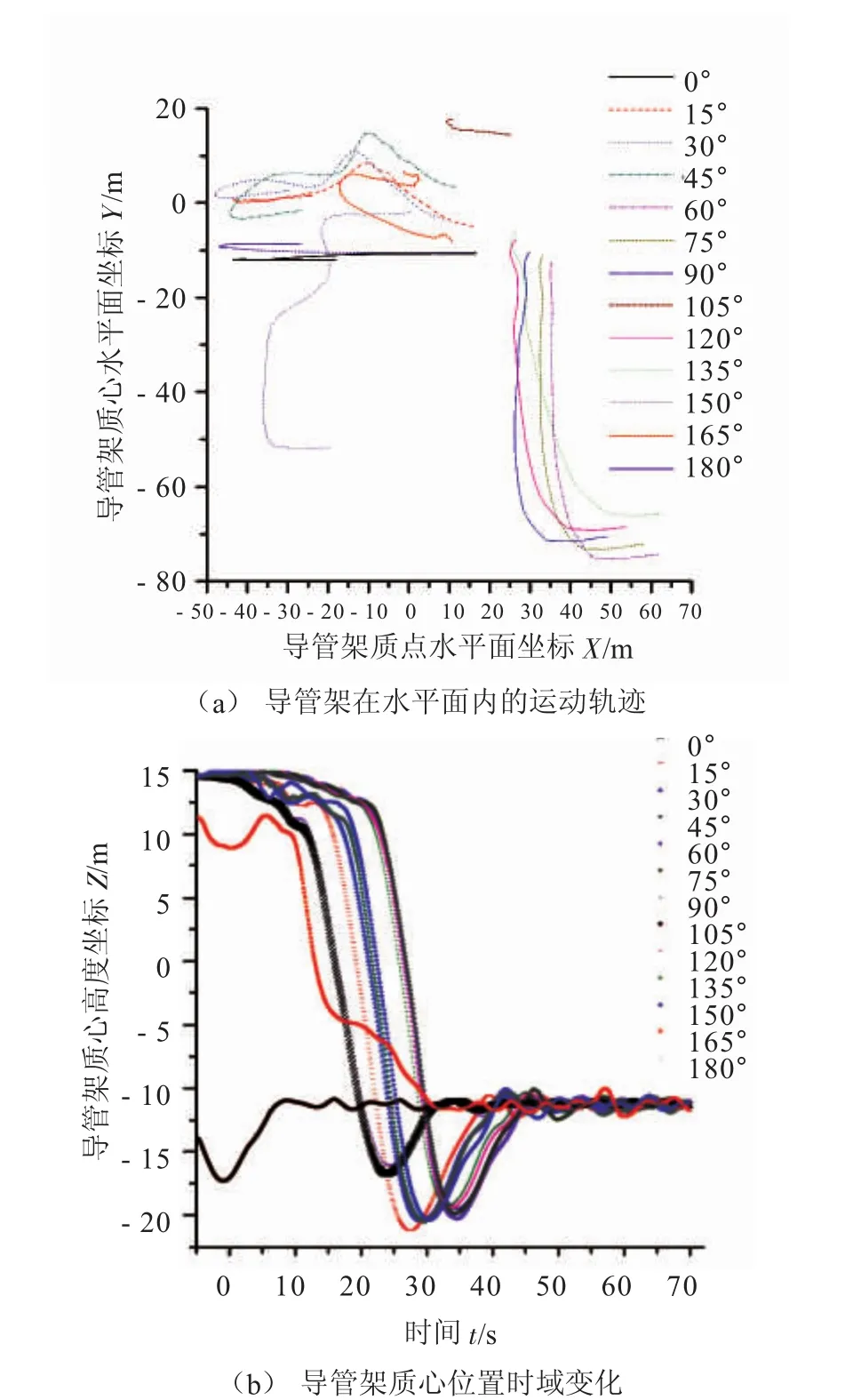
图5 不同浪向下导管架下水时的轨迹

（2）当浪向为105°时，导管架在水平面内的轨迹近似为一段倾斜度较小的斜线，其质心大体在10 m＜X＜25 m，55 m＜Y＜20 m的区域内运动；当浪向为150°时，其在水平面的轨迹近似为两段Y（Y=-53 m和Y=-3 m）值不同的平行直线，其质心大体在-35 m＜X＜5 m，-53 m＜Y＜-3 m的区域内运动；当浪向为165°时，其质心轨迹为在-15 m＜X＜15 m，-8 m＜Y＜7 m的区域内做不规则的曲线运动。

（3）观察不同浪向下导管架质心位置的时域变化发现：除165°和105°浪向时外，不同浪向下导管架质点高度变化的时域图像有着很强的相似性，都是在还未脱离驳船时其质心位置为一正值且基本不变，当导管架下水的一瞬间，由于下水瞬间的冲载荷及导管架本身惯性的作用导管架会继续下沉一段距离，进而使得其质心位置迅速变为负值，下水后随着导管架没入水中体积的不断增大，其受到的浮力不断增大，当浮力值大过重力值时，导管架自身浮力的作用使得导管架下水后的速度逐渐降低为0后开始反向加速上浮，最终其质心位置在一恒定水深不变，且由于不同浪向下导管架脱离驳船的时刻不同，其入水时的初速度也不尽相同，使得其质心位置变为负值的时刻及下潜深度也不尽相同。

（4）当浪向为165°时，导管架在垂直方向上下沉入水后其垂直下水速度只有随着浮力的增大而减小至0的过程但没有速度变为0后反向加速的过程，这是浪向为165°时导管架水下垂直速度变化情况明显不同于其他浪向时的一个显著特征；当浪向为105°时，由于此时导管架在达到静平衡后迅速横滚入海，没有在驳船上滑行的过程，因此在此浪向下其质心坐标迅速变为负值，但也正因为在此浪向下导管架没有在驳船上滑行，导致导管架下水的速度相对较小，因此在此浪向下导管架下潜的最深深度比其他浪向（165°浪向除外）时小；除165°浪向时外，其余浪向下导管架下水后的过程中其垂直方向上的速度均存在一个先减速到0后反向加速又减速到0的阶段。

3.3 不同浪向下导管架的速度及加速度

不同浪向下导管架下水过程的速度、加速度分别见图6、图7。

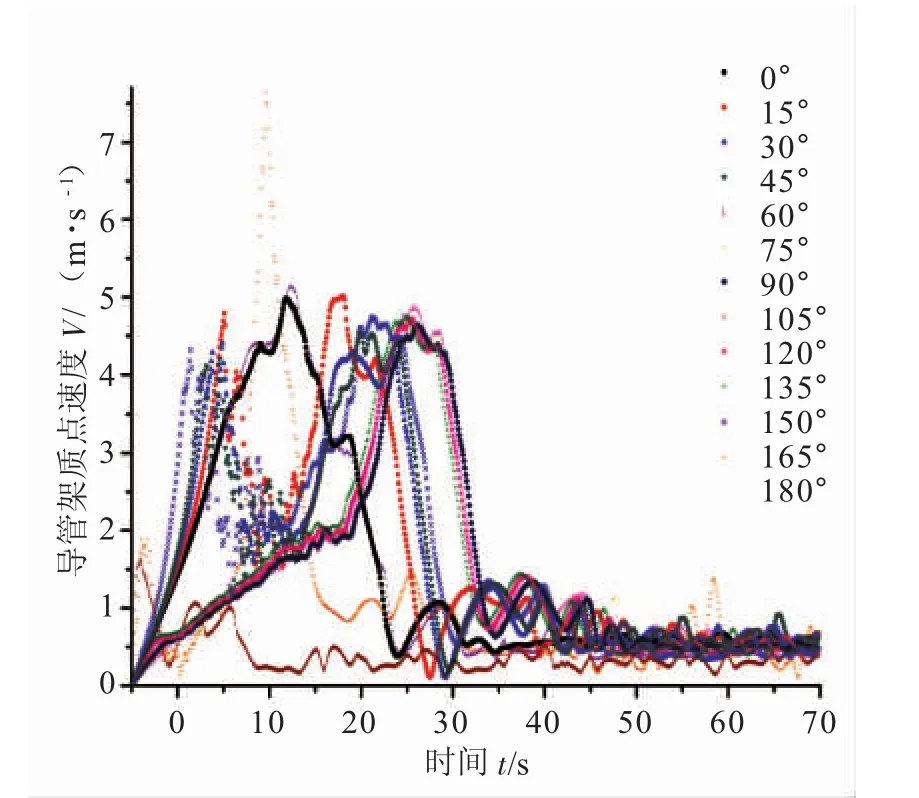
图6 不同浪向下导管架下水过程的速度变化曲线

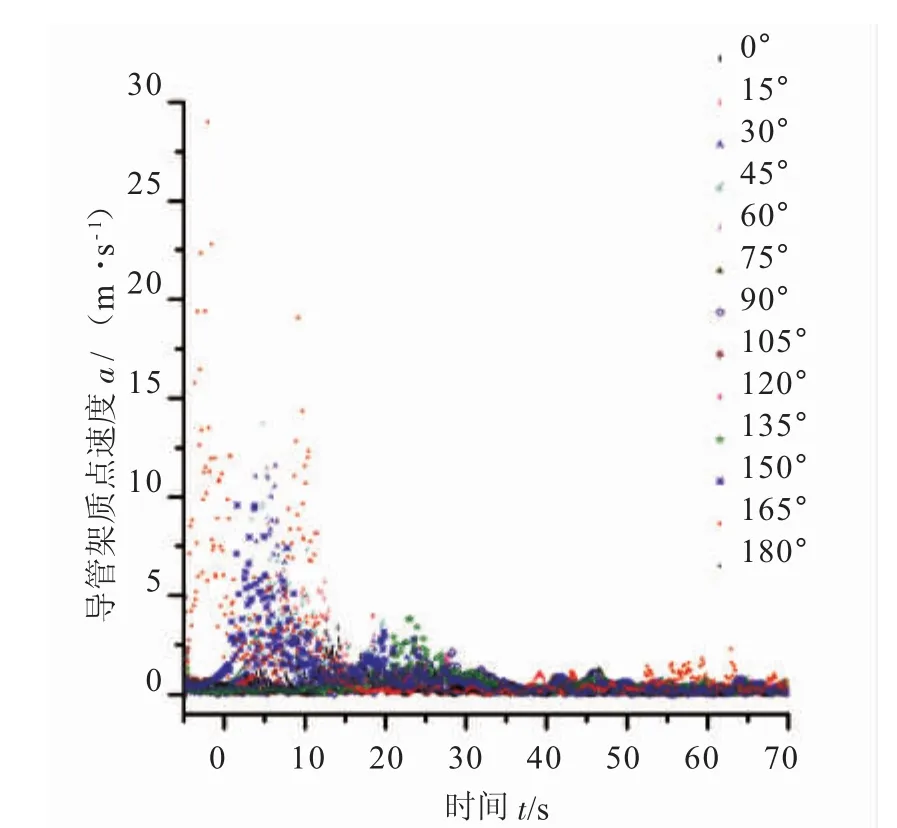
图7 不同浪向下导管架下水过程的加速度变化曲线

观察图6、图7可发现：

（1）除105°浪向时外，其他各个浪向时导管架质点的速度时域曲线变化趋势呈现一定程度的相似性，这某种程度上验证了3.2中对于导管架质点速度变化趋势的分析；同在3.2节中关于浪向为105°时导管架速度的变化趋势也在这里得到了验证；不同浪向时由于导管架脱离驳船滑入水中的时刻不同，导致其速度最大值在时域上出现的时刻也不同。

（2）观察不同浪向下导管架质点下水时的加速度曲线发现：在导管架从驳船甲板开始下滑到导管架入水的这一阶段是导管架加速度不断增加的阶段，在导管架滑入水中后，由于浮力及水的阻碍作用，导管架的加速度迅速减小到0后再反向加速，这样随着导管架速度方向的改变，导管架浮力开始减小，而水的阻力与重力的合力不断增大，进而使得在这些力的合力作用下导管架向上的加速度又开始逐渐减小，最终当导管架再次浮出水面后导管架受到的浮力与导管架的重力再次相等，导管架的加速度再次变为0；导管架质点下水的速度及加速度图像验证了3.2节分析的正确性。（图中关于导管架质点的速度及加速度均取的是数值的大小）

3.4 不同浪向下导管架的角速度及角加速度

不同浪向下导管架下水过程的角速度、角加速度分别见图8、图9。

图8 不同浪向下导管架下水过程的角速度

图9 不同浪向下导管架下水过程的角加速度

（1）观察不同浪向下导管架质点下水过程的角速度图像发现：不同浪向下导管架在下水过程中发生明显地大幅度转动的时刻是不同的；对105°浪向而言，导管架明显大幅度转动发生在其从驳船上横滚入海的瞬间，滚入海中后由于海水的黏性及阻碍作用其转动角速度迅速被降到一个较低的值，然后其转动角速度在这一数值上维持小范围的波动状态；对于其余浪向而言，其转动角速度的最大值发生在导管架脱离驳船滑入海水中的瞬间，具体到某一浪向而言，因为浪向的不同会导致导管架脱离驳船的时刻不同，进而表现在角速度时域图像上就显示为不同浪向下导管架质点的转动角速度最大值出现的时刻也不尽相同，这也与3.1节中提出的不同浪向下导管架下水时刻有所不同的结论相互验证。

（2）观察不同浪向下导管架质点下水过程的角加速度图像发现：在浪向为165°时其角加速度的最大值要远远大于其他浪向时角加速度的最大值，这也是因为在该浪向时导管架没入水中的深度较小，进而使得其在上浮的过程中受到的水阻力较小，进而使得浮力对其产生的回复力矩较其他浪向而言较小造成的，观察3.2节中导管架质心高度时域变化图像可以验证这一点；在两个时刻不同浪向下导管架质心角加速度较大，一个时刻是在导管架刚开始从驳船上沿滑道滑入海水的瞬间，一个时刻是在导管架脱离驳船的瞬间。

4 结论

（1）在不同浪向，甲板对导管架的垂直支持力在数值的大小和时域的分布上各不相同；不同浪向下，导管架脱离甲板滑入海水中的时间也不尽相同；导管架下水所用时间越久，甲板支撑力曲线变化越和缓且甲板支撑力最大值越小。

（2）在浪向为105°时导管架不会沿着滑道滑入海水中，而是会与两个侧壁发生急剧的碰撞挤压及摩擦，进而横滚入海，这是一种极其危险的情况，因此应避免在这种浪向下施工；在浪向为45°、75°、90°、120°、180°时，导管架与滑道左侧壁、右侧壁均无任何形式的接触力的作用，如在这些浪向下进行导管架下水作业，可以避免或减少导管架与滑道侧壁的碰撞。

（3）浪向的改变对导管架质心轨迹在水平面内的影响较大，而在竖直高度上导管架质心的位置变化随着浪向的改变在时域上会有所不同，但其质心高度位置图像整体呈现一定的相似性；当浪向为165°时，导管架在垂直方向上下沉入水后其垂直下水速度只有随着浮力的增大而减小至0的过程，但没有速度变为0后反向加速的过程，这是当浪向为165°时导管架水下垂直速度变化情况明显不同于其他浪向的一个显著特征。

（4）由于不同浪向时导管架脱离驳船滑入水中的时刻不同，导致其速度最大值在时域上出现的时刻也不同；对于绝大多数浪向而言，导管架都要经历下水前加速，下水后由于浮力及水的阻碍作用，导管架的加速度迅速减小到0后再反向加速，这样随着导管架速度方向的改变，导管架浮力开始减小，而水的阻力与重力的合力不断增大使得导管架向上的加速度又开始逐渐减小，最终当导管架再次浮出水面后导管架受到的浮力与导管架的重力再次相等，导管架的加速度再次变为0的这样一个过程。

（5）不同浪向下导管架在下水过程中发生明显地大幅度转动的时刻是不同的，对于绝大多数浪向而言，其转动角速度的最大值发生在导管架脱离驳船滑入海水中的瞬间；不同浪向下导管架质心角加速度在两个时刻较大，一个时刻是在仿真开始导管架刚开始从驳船上沿滑道滑入海水的瞬间，一个时刻是在导管架脱离驳船的瞬间。

[1]C H J O，KS KIM，S H LEE.Parametric study on offshore jacket launching[J].Ocean Engineering，2002（29）：1 959-1 979.

[2]CHAKRABARTI K S.Scale effects on a unique launch sequence of a gravity-based structure[J].Applied Ocean Re search，1995（17）：33-41.

[3]刘应中，郭亚斌，顾树华.导管架下水过程的理论计算和模型试验[J].中国造船，1986（1）：1-11.

[4]樊之夏.深水导管架安装研究 [J].中国海洋平台，2003（2）：27-29.

[5]杨晓钢.深水导管架滑移下水的安装分析技术和设计方法[J].中国造船，2003（44）：259-270.

[6]Engineering Dynamics.SACS Program Manual[M].New York：Ultramarine Publishing，1999.

[7]蔡元浪，田锋，刘鹏.深水导管架的运输分析[J].中国造船，2017，48（S）：330-335.

[8]朱克强，郑道昌，周江华，等.生产驳船多点系泊定位动态响应[J].中国航海，2007，71（2）：6-9.

[9]ZHU Keqiang，CAIYing，YU Chunling，etal.Nonlinear hydrodynamicresponse of marine cable -body system undergoing random dynamic excitation [J].Journalof Hydrodynamics，2009，21（6）：851-855.

[10]ORCAFLEXHelp File and User Manual[Z].

[11]朱克强，李道根，李维扬.海洋缆体系统的统一凝集参数时域分析法[J].海洋工程，2002，20（2）：100-104.

[12]YANG Bingka，ZHU Keqiang，ZHU Yanjie，et al.Dynamic response of towed line array [J].Journal of Hydrodynamics，2013，25（4）：616-619.

[13]朱艳杰，朱克强，杨冰卡，等.基于凝集质量法的海洋缆索动力学建模与仿真技术[J].海洋工程，2014，32（1）：112-116.

Dynamic analysis for jacket launching under different wave directions

ZHANG Dapeng1，BAIYong1，ZHU Keqiang2，LIU Jian2，GUIQinqin2
1.College of CivilEngineering and Architecture，Zhejiang University，Hangzhou 310058，China
2.Faculty of Maritime and Transportation，Ningbo University， Ningbo 315211，China

Jacket launching is a complex process，jacket may touch seabed due to incorrect operation.In order to increase the safety and reliability of construction，it is necessary to analyze the jacket launching process.Based on the lumped mass method and the specific structure parameters of a certain jacket，the jacket is discretized into the lumped mass model.Combined with the specific process of launching jacket and by means of necessary simplification，the dynamic model of the jacket during the launching process under different wave directions has been established by OrcaFlex software.It is found that the change of wave direction affects the launching process obviously：the time of the jacket sliding into sea from the barge deck changes with deferent wave direction，the influence of wave direction change on the jacket mass center curve in horizontal plane is big；and the jacket mass center in vertical plane changes with different wave direction in time-domain，but the mass center curves have certain similarity.The calculation results have a certain guiding significance for the study of the jacket launching.It can provide technicalsupport for the study of the jacket launching.

lumped mass method；OrcaFlex；jacket launching；dynamic analysis

10.3969/j.issn.1001-2206.2017.05.002

长江学者和创新团队发展计划项目（IRT0734）；国家自然科学基金资助项目（11272160）；近岸孔隙结构物内流体运动特征的SPH数值模拟研究（Q16E090001）资助。

张大朋（1987-），男，山东聊城人，浙江大学在读博士研究生，主要从事船舶与海洋工程结构物动态响应方向的研究。Email：baiyong@zju.edu.cn

2017-04-10