基于二阶滑模算法的船舶航向控制

刘勇，卜仁祥，孙大铭

（大连海事大学 航海学院，大连 116026）

基于二阶滑模算法的船舶航向控制

刘勇，卜仁祥，孙大铭

（大连海事大学 航海学院，大连 116026）

针对非线性、易受外界扰动的欠驱动船舶航向控制系统，基于滑模控制算法的理念，直接对二阶航向控制系统中的控制输入进行设计，提出一种二阶滑模控制算法，通过设计合理的李雅普诺夫函数及利用其稳定性理论对系统的稳定性进行了分析，并利用“育龙”轮运动数学模型进行计算机模拟仿真，验证了该控制算法的合理性及有效性。该算法避免了计算中的维数膨胀问题，无需对不确定的外界摄动进行定性估计，可以保证闭环控制系统的渐近收敛及稳定。仿真结果表明，根据该控制算法所设计的控制器，能够有效解决非线性航向控制系统中存在的抖振、超调以及不能在有限时间内快速收敛的问题，而且对外界干扰以及系统摄动不敏感、具有强鲁棒性，具有很好的实践应用价值。

欠驱动船舶；船舶航向控制；二阶滑模

常规水面船舶的控制系统具有欠驱动特性［1］以及非完整约束特点［2］，模型的非线性［3］、不确定性［4］和易受外界干扰等特点［5］。

针对航向控制问题，刘程［6］等设计了一种自适应模糊跟踪控制算法，确保了闭环控制系统的稳定性，同时能够使得航向的跟踪误差任意小。朱齐丹［7］等针对船舶航向控制系统中参数不确定性和外界干扰随机性的特点，将反步法和非线性滑模观测器相结合，设计了一种能够保证闭环系统全局渐近稳定的控制算法。李芸［8］等针对船舶易受不确定的外界干扰的特性，将非线性干扰观测器的设计原理和扩张状态观测器可以抑制状态干扰的特性相结合，设计出一种新的扩张干扰观测器，有效的减少了滑模控制的抖动影响，同时对干扰具有良好的抑制性能。

二阶滑模控制算法作为高阶滑模控制算法中的特殊情形，具有设计简洁、有限时间收敛、鲁棒性强、对外界干扰及系统摄动不敏感的诸多优点，同时能够有效地削弱传统一阶滑模中存在的“抖振”现象，因此受到国内外诸多学者的青睐。针对滑模控制算法，Modirrousta，A［9］等提出一种二阶滑模控制算法，该算法对外界干扰不敏感，具有很强的鲁棒性，有效解决了系统抖振问题。Zhou［10］等提出一种二阶滑模控制算法应用到导弹控制系统中，有效解决了系统抖振问题并且使系统迅速准确的进行了目标的跟踪。Shtessel，Y［11］等设计了一种自适应滑模控制器，仿真结果轨迹平滑、跟踪准确，可以有效的应对不确定的外界因素的干扰。Shtessel，Y［12］等为一阶和二阶动态控制系统设计了一种二阶滑模控制算法，可以确保系统在有限的时间内收敛，跟踪准确，控制效果良好。Levant［13-14］在文献中系统地阐述了二阶滑模控制方法，并对二阶滑模控制算法的设计原则进行了详细的表述。随后，在文献中提出了基于输出反馈控制的高阶滑模控制算法。李雪冰［15］等将加幂积分技术应用到传统的二阶滑模算法中，设计了一种新的二阶滑模控制算法，利用倒立摆控制系统验证了系统可以在有限时间内稳定。袁赣南［16］等为了削弱传统滑模控制系统中存在的抖振现象以及简化二阶滑模控制器的设计过程，提出一个二阶滑模控制系统的滑模到达的有效条件，结果表明能有效抑制控制系统中的抖振，具有很强的鲁棒性和良好的控制性能。

本文针对欠驱动船舶非线性航向控制系统，运用滑模控制思想，提出一种二阶滑模控制算法，并利用该算法设计二阶滑模控制器。利用“育龙”轮操纵运动数学模型，针对在不同外界干扰下的航向阶跃响应进行了仿真，结果表明控制器对不确定的外界干扰以及系统的摄动不敏感，算法具有很强的鲁棒性和良好的控制性能，有效的减弱了系统的抖振和解决了航向不能快速稳定问题。

1 二阶滑模控制算法

1.1 问题的描述

考虑以下单输入单输出控制系统：

式中，s∈Rn为状态变量，u∈R为控制输入，d(t)为不确定的外界干扰，y为系统输出。

对于系统（1）而言，控制系统的设计目标是设计合理的二阶滑模控制算法，使上述系统在外界干扰和系统摄动不确定的情况下能够达到渐进稳定。

1.2 二阶滑模控制算法

滑模控制的优点是能克服系统的不确定性，对不确定的外界干扰和未建模动态具有很强的鲁棒性，尤其是对非线性系统具有良好的控制性能和效果。对于系统（1），控制的目标为设计合理的控制输入u，使状态变量在有限的时间内收敛并稳定。

本文设计的二阶滑模控制算法如下：

将式（2）代入到系统（1）中，得：

式（4）可以写为：

李亚普诺夫函数设计如下：

系统稳定性分析如下：

根据式（9）得：

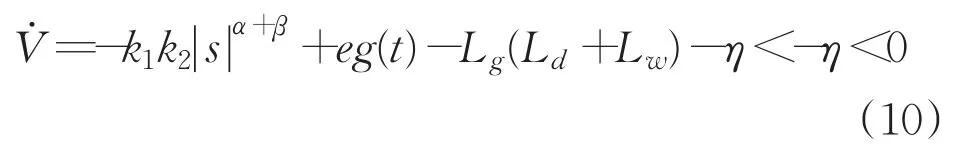
因为V＞0且所以系统渐进稳定。

2 基于二阶滑模算法的航向控制器的设计及仿真

2.1 船舶航向控制问题

对于非线性航向控制系统：

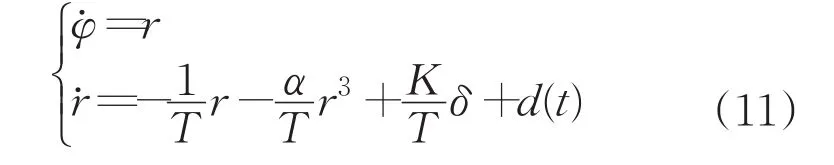
其中，φ为航向，r为转首角速度，K,T为有界的船舶参数，α为非线性项参数，d(t)为连续的外界干扰，δ为舵角。

船舶非线性航向控制问题为：确定δ，使φ→φd及r→0，φd为计划航向，通过坐标转换及平移，控制问题可简化为使φ→0。

舵机响应模型［2］一般为：

其中，δr为命令舵角，TE为舵机时间常数。

2.2 船舶航向二阶滑模控制算法

对于系统（11），令：

非线性航向控制系统（11）可转化为：

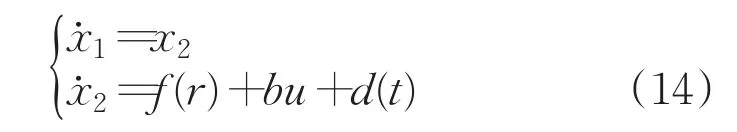
因此，非线性航向控制系统（11）及系统（14）的二阶滑模控制算法为：

通过设计此控制律使得系统在外界干扰不确定的情况下，保持系统稳定收敛的不变性，具有很强的鲁棒性和很好控制效果。

2.3 船舶航向控制仿真与分析

为验证本文设计的控制算法的有效性及对船舶航向的控制效果，运用MATLAB的Simulink仿真环境设计船舶运动数学模型（11）及船舶航向控制程序，对控制器中各参数进行合理的设计，并以“育龙”轮为对象，其中K=0.478，T=216，α=30，针对不同外界干扰情况下控制器的控制品质进行计算机模拟仿真，并进行了相应的对比分析。

仿真过程中，程序中各参数设置如下：k1=1；k2=0.01；k3=0.1；k4=1。将二阶滑模控制算法转化为程序，引入到航向控制器中，得到控制输入，实现闭环系统的稳定、准确跟踪。对于外界干扰的设置，本文将外界干扰直接设置在船舶模型里面，来验证控制器的强鲁棒性以及对外界摄动的不敏感性。

图1 无干扰时航向改变10°的仿真结果

图2 有外界干扰时航向改变10°仿真结果

图1表明航向的仿真曲线平滑、跟踪稳定准确，超调和抖振很小，舵角曲线有一定的超调符合航海实际。船舶进行转向的时候，为了防止船舶运动轨迹出现频繁的“S”形，舵角需要提前进行相应的压舵调节来控制转首角速率和航向偏差，使得船首迅速而准确的稳定，结果表明控制器在无外界干扰的情况下具有良好的控制品质。

图2表明航向仿真曲线在有外界干扰的情况仍然平滑、跟踪稳定准确，超调和抖振很小。不同的是舵角曲线，在有外界干扰的情况下，船舶需要进行较大的舵角来抵抗外界干扰，来确保船舶航向的快速响应和稳定，结果表明控制器对外界干扰的扰动不明显，具有很强的鲁棒性。

3 结论

本文针对欠驱动船舶非线性航向控制系统，利用滑模控制思想，直接设计航向控制系统的控制输入，提出一种新的二阶滑模控制算法，利用李亚普诺夫稳定性理论证明了系统的稳定，设计的二阶滑模船舶航向控制器，可以确保航向控制系统在有限时间内稳定收敛。

本文设计的二阶滑模控制算法计算量较少，有效的避免了传统滑模控制计算中容易出现的“维数膨胀”问题。利用本文提出的控制算法所设计的控制器对外界干扰等不确定因素的摄动不敏感，具有很强的鲁棒性和良好的控制效果。控制算法很好的削弱了二阶航向控制系统中超调和抖振问题。

［1］Mahmut，Arjan，Harris N.Dynamics and control of a class of underactuated mechnical systems［J］.IEEE Transactions on Automatic Control，1999，44（9）：1663-167l.

［2］卜仁祥.欠驱动水面船舶非线性反馈控制研究［D］.大连：大连海事大学，2008.

［3］李铁山，杨盐生，郑云峰.不完全驱动船舶非线性控制［J］.交通运输工程学报，2003，3（4）：39-43.

［4］郭晨，汪洋，孙富春，等.欠驱动水面船舶运动控制研究综述［J］.控制与决策，2009（03）：321-328.

［5］卜仁祥，刘正江，胡江强.基于动态非线性滑动模态的欠驱动船舶直线航迹控制［J］.清华大学学报：自然科学版，2007（S2）：1880-1883.

［6］刘程，李铁山，陈纳新.带有舵机特性的船舶航向自动舵DSC-MLP设计［J］.哈尔滨工程大学学报，2012，33（01）：9-14.

［7］朱齐丹，周芳，赵国良，等.基于反步法和滑模观测器的船舶航向控制［J］.华中科技大学学报：自然科学版，2009，37（04）：122-125.

［8］李芸，白响恩，肖英杰.基于新型扩张干扰观测器的船舶航向滑模控制［J］.上海交通大学学报，2014，12（48）：1708-1713.

［9］Modirrousta A，Sohrab M，Dehghan S.A modified guidance law for ground moving target tracking with a class of the fast adaptive second-order sliding mode［J］.Transactions of the Institute of Measurement and Control，2016，38（07），819-831.

［10］Zhou Huibo，Song Shenmin，Song Junhong，et al.Design of second-order sliding mode guidance law based on the non-homogeneous disturbance observer［J］.Journal of Control Science and Engineering，2014（2014）：1-10.

［11］Shtessel Y，Taleb M，Plestan F.A novel adaptivegain super-twisting sliding mode controller：Methodology and Application［J］.Automatica，2012，48（05）：759-769.

［12］Shtessel Y，Kochalummoottil J，Edwards C.Continuous adaptive finite reaching time control and secondorder sliding modes［J］.IMA Journal of Mathematical Control and Information，2013，30（01）：97-113.

［13］Levant A.Principles of 2-sliding mode design［J］.Automatica，2007，43（4）：576-586.

［14］Levant A.Higher-order sliding modes，diffierentiation and output-feedback control［J］.International Journal of Control，2003，76（9）：924-941.

［15］李雪冰，马莉，丁世宏.一类新的二阶滑模控制方法及其在倒立摆控制中的应用［J］.自动化学报，2015，01（41）：193-202.

［16］袁赣南，左志丹，曲桂婷，等.二阶滑模变结构控制系统的滑模到达条件［J］.华中科技大学学报：自然科学版，2013，06（41）：70-75.

［17］杨永彬，赵贺伟，李涵.基于反演设计的无人水下航行器自适应二阶滑模控制［J］.海军航空工程学院学报，2016，02（31）：152-158.

Ship Course Control Based on Second Order Sliding Mode Method

LIU Yong，BU Renxiang，SUN Daming
（Navigation College，Dalian Maritime University，Dalian 116026）

According to sliding mode control ideas，a control input is designed and a new adaptive second order control algorithm is proposed for second order course control system of underactuated ships with nonlinearity，and uncertain external disturbances.The stability of control system is proved by Lyapunov stability theory and numerical simulation is carried out to validate the reasonableness and validity.The algorithm avoid dimensional explosion and without uncertainty estimating and it can guarantee the convergence and stability of closed-loop control system.Numerical simulation results verify the controller who is proposed by this algorithm is insensitive to external disturbances and system perturbation and has the invariability and excellent robustness，and it can effectively solve the problem of chattering and divergent in the nonlinear course control system which has a good practice value in the future.

underactuated ship；ship course control；second order sliding mode

U664.82

A

1672-9870（2017）04-0069-04

2017-05-26

辽宁省自然基金项目（201602084）；中央高校基本科研业务费专项资金资助项目（3132016008）

刘勇（1985-），男，硕士，讲师，E-mail：liuyong_dlmu@163.com